Inverse Filter (Mourjopoulos theory)
The creation of a causal, stable inverse filter for a given mixed-phase impulse response is generally an impossible task, and only approximate solution are available for this problem. This argument was deeply investigated by Mourjopoulos [12], particularly with the goal of obtaining a digital equalisation of the room's response. Among the various techniques explored by him and others, the straightforward least-squares technique was chosen, as clearly explained in the Mourjopoulos paper. A least-square problem is set up, requiring that the unknown inverse filter, g(t), when convoluted with the original impulse response h(t), produces as result a delayed Dirac's delta function. After proper formulation, a standard linear equation system is formed, in which a square matrix [R] is multiplied by the unknown vector {g}, producing the known terms vector {k}.
[R] · {g} = {k}
It turns out that the latter is simply a delayed, time reversed copy of the original impulse response h(t), while the [R] matrix is a Toepltiz matrix, in which the first row is simply the autocorrelation function of the original signal, and each of the subsequent rows is obtained by circular permutation (1 sample to the right) of the upper row. Fortunately, the solution of a Toeplitz system is possible with standard algorithms, included in any library of scientific functions. This way only the first row of the matrix has to been generated and stored, and the computation is thus possible also for very long IRs on standard computers. The successful creation of an inverse filter is anyway not always easy: if the frequency response of the original impulse response has very deep valleys, these tunr out in strong peak of the inverse filters, which tends to become quite long. Furthermore, if the high frequency part of the spectrum of the original signal has low energy (this is common when an anti-aliasing filter is used), the inverse filter has maximum amplitude at these inaudible frequencies, and a very low gain at the lower frequencies, so that the filtered signal can fall below the numerical noise floor. For these reasons a certain pre-processing of the original impulse response is usually needed before attempting its inversion, but in this field only the experience and skillness of the user can be useful. Anyway, the inverse filter can always be quickly checked, applying it to the original impulse response or to other raw signals, by means of the convolution module. Often our ears are the better instrument for checking if the inverse filter is acceptable, or if it produces intolerable artifacts.
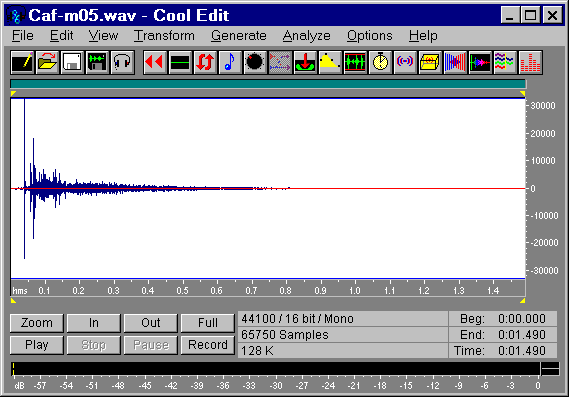
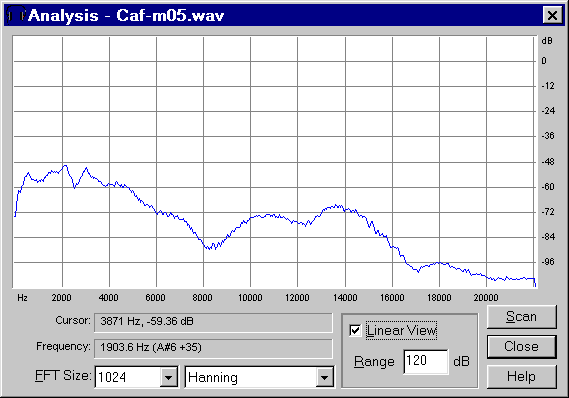
For example, the following picture reports an impulse response of a room excited by a loudspeaker and recorded by a microphone placed at a certain distance from it, so that a lot of reverberation and wall reflections are evident. This causes also an evident frequency response colouration, as shown in the same picture.
 |
 |
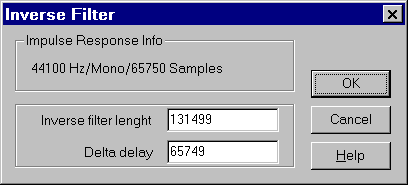
Invoking the Transform / Inverse Filter module, a dialog box appears, asking for the length of the inverse filter (in samples) and for the wanted delay of the signal (this is necessary for ensuring that the inverse filter is causal, and is usually chosen around half the length of the filter). Morjopoulos suggests a filter length approximately equal to the reverberation time of the room, although in some case shorter filters works reasonably well.
 |
 |
Then the solution of the Toeplitz problem is started: the computation time increases with the square of the filter length, because it is an iterative algorithm, which loops for a number of times equal to the filter length, and the number of operations inside each cycle is also proportional to the number of unknowns.
After a few seconds, anyway, a dialog box is displayed, informing the user that the inverse filter has been successfully stored in the Windows clipboard.
From there it can be recovered, opening a new instance of CoolEdit and pasting from the Windows clipboard. The following figure reports the inverse filter of the room response.
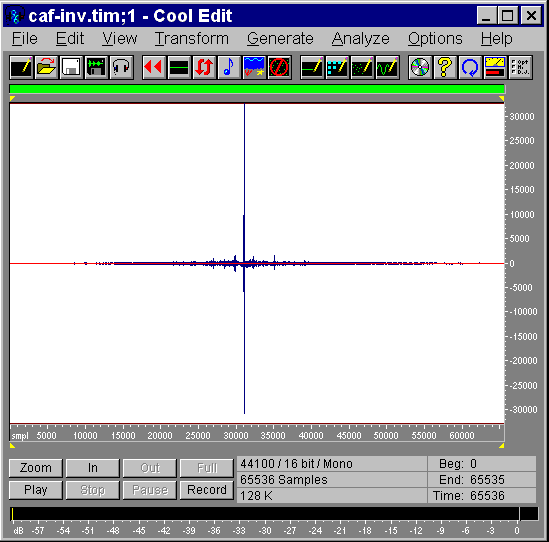 |
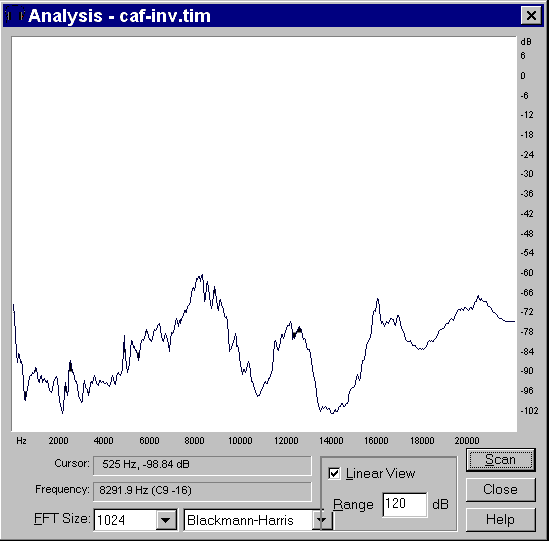 |
The verification of the proper working of the filter can be done by convolving the original impulse response with it. This is shown in the following pictures: an almost perfect Dirac's delta function has been obtained in the time domain, and in the frequency domain the response is flat.
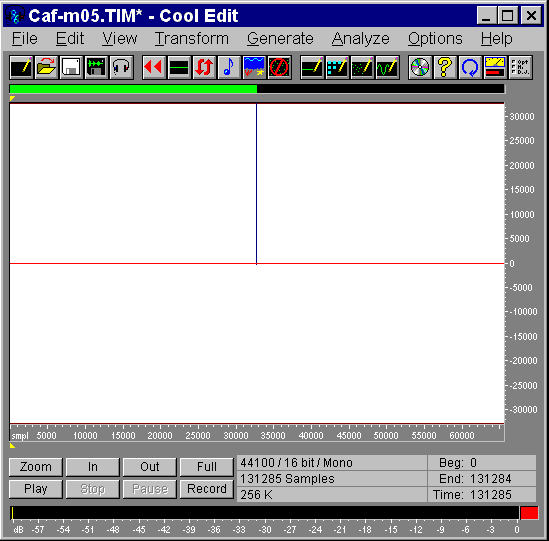 |
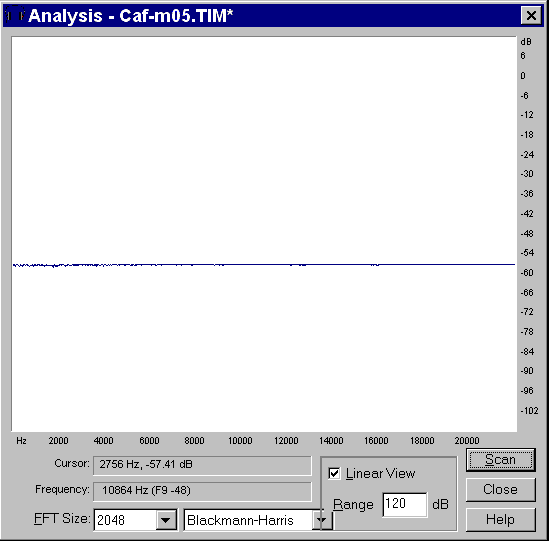 |
This way the effect of the transducers can be removed from a measured impulse response, or in general any recording done through a linear channel can be cleaned from its effects: in principle, a recording affected by too much reverberation can be de-reverberated, although this effect is quite difficult to obtain, because even a small difference in the position of the source and the receiver makes the inverse filter unmatched with the signal. Morjopoulos already addressed this problem [12], and an enhanced dereverberation module is being developed now, following his principles.