Generate MLS signal - Generate IRS signal
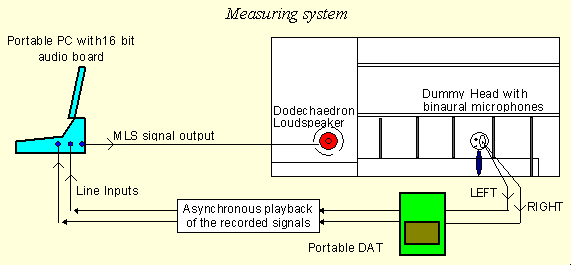
These two modules perform very similar tasks: they create the excitation signals, which are required for exciting the system when doing impulse response measurements with the following scheme:
 |
MLS stands for Maximum Lenght Sequence, IRS stands for Inverse Repeated Sequence. Both these excitation signals are defined as a pseudo-random sequence of binary digits (0 and 1), built with a complex number-theory technique.
The important properties of these sequences are the following:
- Periodic: the signal can be repeated continuously, through the "Loop Mode" of playback in CoolEdit. Averaging the system's response over many repeated sequences, the Signal-To-Noise ratio can be largely improved
- Binary: as the signal switches between only two extreme values, the crest factor is 0 dB, and this gives maximum power within a constrained amplitude.
- Flat spectrum: the frequency content of these signal is almost perfectly flat, resembling an ideal "white noise".
- Autocorrelation is a Dirac's Delta function, and this enables the deconvolution of the system's impulse response by correlating the measured response with the original sequence.
- The MLS sequence has the great advantage of making it possible the correlation process with a very fast algorithm, the Fast Hadamard Transform, which yields the result through a limited number of sums and subtractions, directly in the time domain. The disadvantage is that, if the system exhibits some kind of non-linear distortion, this can cause the appearance of some spurious "phantom echoes" at some well-defined tap position.
- The IRS sequence is made of two MLS sequences, the second being an inverted copy of the first one. This means that a 2*N sequence is required for measuring an N-point impulse response, doubling the measurement time. Furthermore, the fast Hadamard transform cannot be used for deconvolving the result, and the usual processing in the frequency domain (by use of very large FFTs and IFFTs) is required during the correlation. Although with this sequence the measurement is slower, it exhibit a larger immunity to distortion, and particularly to odd-order distortion.
Aurora makes it possible to generate MLS and IRS sequences up to order 21: this means that the maximum length of the measured IRs will be 2^21-1, that is 2,097,151 samples, corresponding to more than 47 s at a sampling frequency of 44.1 kHz !!!
For the most commonly used orders (14, 15, 16 and 17), more than one sequence is available (labelled as 16A, 16B and 16C, for example). Each of them is produced according to a different permutation of the numerical basis, and thus the results are uncorrelated. In case of distortion, each of these sequences produces spurious echoes at different positions, so that they can be easily identified and removed.
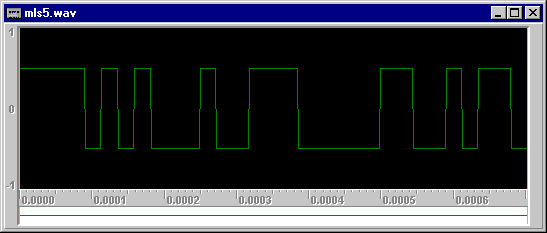
The following picture shows an MLS sequence of order 5 (period of 31 samples):
 |