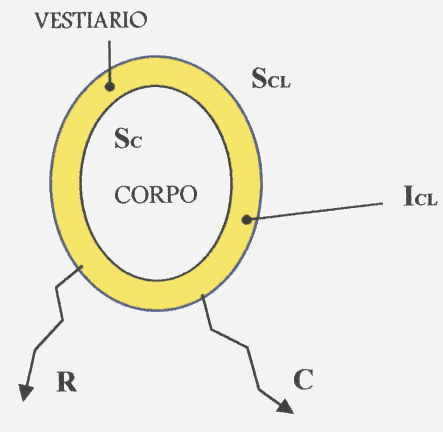
Comfort termoigrometrico – metodo di Fanger
- Il bilancio energetico di un organismo umano e le leggi a cui esso è sottoposto
- Lo psicometro
- Il metodo ASHRAE con relativa tabella
- Le condizioni di benessere termico secondo il criterio di Fanger e diagramma
- Diagramma degli abbigliamenti tipici per attività sedentarie in interni
- Esempio
Il bilancio energetico di un organismo umano può essere rappresentato, utilizzando grandezze in valore assoluto, dalla relazione:
M – LP – LG – U – Ed – Es – Er – VS = R + C (1)
dove:
M produzione interna di calore nel corpo umano (energia associata al metabolismo),
LP energia utilizzata dall’organismo per l’attività polmonare,
LG energia utilizzata dall’organismo per compiere lavoro contro la forza di gravità,
U energia accumulata nell’organismo,
Ed calore disperso per evaporazione e diffusione di vapore acqueo attraverso la
pelle,
Es calore disperso per evaporazione del sudore dalla superficie della pelle,
Ed – Es =WS è un parametro che varia da 0 a 1 e che indica la percentuale di pelle bagnata dal sudore,
Er calore latente disperso per respirazione (sotto forma di vapor d’acqua prodotto),
VS calore sensibile disperso per respirazione,
R calore scambiato per irraggiamento dalla superficie esterna del corpo vestito,
C calore scambiato per convezione dalla superficie esterna del corpo vestito.
La doppia equazione ha questo significato: la produzione interna di calore M meno: il calore disperso per evaporazione dalla pelle (Ed + Es) e attraverso il meccanismo della respirazione (Er – VS), il lavoro meccanico compiuto per il funzionamento interno e contro la forza di gravità, l’eventuale accumulo di energia, è uguale al calore dissipato alla superficie esterna dei vestiti per irraggiamento e convezione (R + C). Essa, vista nelle sue varie espressioni consente di individuare tre valori fondamentali per la temperatura, cioè la temperatura interna del corpo TI, la temperatura esterna TCL, quella dell’aria TA, due coefficienti di scambio ICL e il coefficiente globale di scambio convettivo a = hC + hR e il calore metabolico M’.
La dispersione di calore per convezione dalla superficie esterna del corpo vestito è così espressa:
C = hC × fCL ( tCL-tA) ( W / m2 ) (2)
dove C rappresenta lo scambio termico convettivo (o calore scambiato per convezione), h
C è il coefficiente di scambio termico o coefficiente di convezione tra superficie esterna ed aria, valore medio riferito all’intera superficie corporea, il cui valore dipende dal tipo di convezione. Per bassa velocità dell’aria("aria ferma") il trasporto di calore avviene per convezione naturale, così che hC è funzione della differenza di temperatura (tCL–tA); per velocità più alte, esiste convezione forzata e hC diventa allora funzione della velocità. Esso vale circa ½× kC, ove kC è il coefficiente di scambio evaporativo(i due fenomeni di evaporazione e di scambio termico sono tra loro connessi).fCL è il rapporto tra SCL (superficie esterna degli abiti) e SC(superficie del corpo nudo).
(tCL–tA) differenza tra tCL(temperatura superficiale esterna degli abiti) e tA(temperatura di bulbo asciutto dell’aria).
Lo scambio termico convettivo C dipende dalla velocità dell’aria; più velocemente essa ci lambisce, maggiore sarà lo scambio termico convettivo. Infatti per un corpo seduto frontalmente alla corrente d’aria:
hC = 8.3 × v 0.6 ( W/ m2 k) = 5.47( W/ m2 k) (3)
Anche hC quindi dipende dalla velocità dell’aria v[m/s] e fa sì che anche C ne sia influenzato. E’ indifferente se sia l’aria a muoversi o il corpo.
Di solito hC per un corpo con aria di fronte vale fino a 8, 10; in aria ferma vale all’incirca 3, anche se in teoria l’aria è sempre in moto, cioè in ogni ambiente avviene sempre un ricambio.
In condizioni di riposo o in posizione eretta invece si ha:
hC = 2.38 (tCL - tA)0.25 ( W/ m2 k) (4)
Nel caso della convezione forzata, è stato studiato il trasporto del calore convettivo per soggetti in posizione semi-inclinata con flusso dell’aria discendente(dall’alto verso il basso) ed è stata determinata la seguente relazione:
hC = 12.1 Ö v ( W/ m2 k) con v< 2.6 m/s (5)
Nel caso di un corpo eretto, in moto relativo rispetto all’aria, con velocità relativa:
hC = 8.6 × v0.53 ( W/ m2 k) (6)
se per esempio: v = 100 km/h = 27.7 m/s, allora hC = 50 ( W/ m2 k).
La presenza o meno di una certa velocità dell’aria per calcolare il coefficiente di convezione è un problema complicato dal momento che i soggetti sono costituiti dalla compresenza della pelle e dei vestiti e all’esterno di ciò avvengono gli scambi convettivi. Semplificando:

Figura 1 - Ovoide rappresentante il nostro corpo, da cui si dissipa calore per convezione e irraggiamento.
ICL è l’espressione adimensionale della resistenza termica totale tra la pelle e la superficie esterna del corpo vestito, essa rappresenta l’unità di vestiario ed è espressa
in clo.
ICL = RCL / 0.155 (clo) (ove RCL è la resistenza termica specifica pelle+abiti) (7)
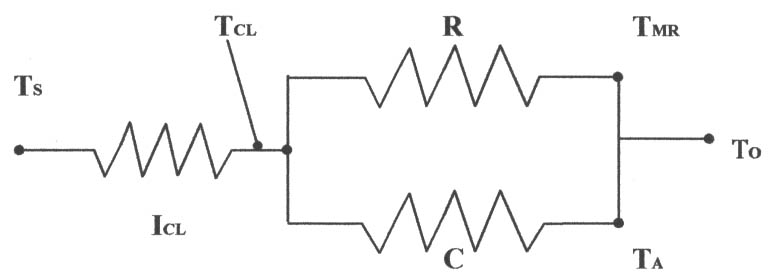
Figura 2- Il fenomeno dal punto di vista elettrico.
dove:
TS rappresenta la temperatura superficiale del corpo nudo.
TCL la temperatura superficiale esterna dei vestiti.
TMR la temperatura media radiante dell’ambiente.
TA la temperatura dell’aria.
TO la temperatura operante, media pesata tra i due valori di temperatura TMR e TA. Quella media radiante incide fortemente sulla operante, tanto che all’aumento di un grado da parte della prima ne consegue l’aumento di due gradi o più per la seconda.
hR il coefficiente di irraggiamento tra superficie esterna e superfici circostanti, dipende da una differenza di temperature ed è un fattore di proporzionalità diretta. Esso è stato definito come un fattore di proporzionalità lineare.
La temperatura operante è: TO = hC × TA + hR × TMR / hC + hR (8)
Da ciò linearizzo lo scambio termico radiante:
R = 3.9 × 10-8 × fCL [TCL4-TMR4] = hR × fCL [TCL-TMR] (9)
per cui il flusso di calore che si scambia per convezione e irraggiamento risulta:
R+C = [hR× (TCL -TMR) + hC× (TCL-TA)]× fCL (10)
ma può anche essere scritto come segue, tramite la TO:
R+C = a × (TCL-TO)× fCL (ove a = hC + hR) (11)
Sostituendo alcuni valori tra cui il coefficiente di adduzione a e la temperatura operante TO ottengo la potenza metabolica:
R+C = a × FCL× fCL (TS-TO) (12)
a è il coefficiente globale di scambio convettivo, che dipende dai due coefficienti rispettivamente di convezione e di irraggiamento (infatti a = hC + hR).
Al crescere della resistenza dei vestiti si riduce lo scambio termico.
FCL è il fattore di incremento della resistenza termica prodotta dal vestiario e tiene conto della diminuzione di temperatura superficiale connessa con il passaggio del calore attraverso gli abiti. Nella sua equazione compare anche ICL, il numero di clo, che indica quanto la persona è vestita.
FCL = 1 / 1+ 0.155× ICL × fCL × hC (13)
Grazie a ciò siamo in grado di sintetizzare il tutto in un’equazione, riuscendo a ricavare le rette di isoriscaldamento di un corpo.
Si sostituiscono nell’equazione del bilancio energetico (1), che esprime il comfort termoigrometrico, le espressioni stabilite precedentemente:
M - LP = M’ - kC× (0.06 + 0.94 Ws)× (PSC - PVA) =
= 0.3035M× (PSC - PVA) + 0.00167M× (Ti - TA)+ a × FCL× fCL× (TS - TO) + U (14)
M rappresenta il metabolismo.
M’ è il metabolismo già ridotto dall’attività polmonare.
(0.06 + 0.94 Ws) = W = percentuale di bagnatura equivalente o valore del rapporto tra la superficie cutanea comunque bagnata e la totale, indica cioè quanto la pelle suda e il suo valore parte da 0.06(espressa in Watt per secondi).
(PSC - PVA) è la differenza tra la pressione di saturazione del vapore a temperatura cutanea e la pressione del vapore nell’aria.
I termini del secondo membro sono legati al volume ventilato polmonare e alla quantità di vapore.
Ti = calore sensibile (riscaldamento).
U= termine di accumulo.
Posso definire un nuovo metabolismo netto, già privato delle temperature che si disperdono all’aumentare del metabolismo:
MS = M’- 0.3035M× (PSC - PVA) - 0.00167M× (Ti - TA) (15)
Dopo di che l’equazione nella sua forma definitiva risulta:
MS - kC× W× (PSC - PVA) = a × FCL× fCL (TS-TO) (16)
MS è il parametro di ingresso primario di tipo metabolico (ci indica quanto è attiva una persona).
kC× W× (PSC - PVA) indica la capacità di smaltire calore attraverso l’evaporazione.
a × FCL× fCL (TS-TO) percentuale di smaltimento; essa dipende dalla velocità dell’aria, dalla temperatura e dai vestiti che indossiamo.
Il parametro più comunemente utilizzato per descrivere lo stato fisico di un determinato ambiente, con riferimento all’organismo umano che deve vivere nell’ambiente stesso, è costituito dalla temperatura dell’aria TA, che consente di valutare numericamente le comuni sensazioni di caldo e freddo. Essa costituisce quindi il modo più semplice, ma anche più facilmente comprensibile, di giudicare l’accettabilità o meno di un certo intorno microclimatico. Tale parametro si rileva con un comune termometro, ad esempio del tipo a bulbo di mercurio.
Poiché gli scambi di calore tra corpo umano ed ambiente avvengono sia per la differenza di temperatura che per differenza di tensione di vapore, quando questi ultimi divengono relativamente importanti, nei confronti dei primi, è chiaro che la conoscenza della sola temperatura dell’aria non è più sufficiente a descrivere il microclima. Il contenuto di vapor d’acqua nell’aria può essere valutato e da esso ottenere il grado igrometrico j ,detto anche umidità relativa u.r., pari al rapporto tra il valore pV della pressione parziale del vapor d’acqua nella miscela e la pressione massima realizzabile pS (tensione di vapore d’acqua alla temperatura TA). L’umidità relativa u.r. rappresenta la presenza percentuale del vapore nell’aria. Essa è misurata dallo strumento chiamato psicrometro, costituito da un termometro il cui bulbo è avvolto entro una garza bagnata: l’aria, lambendo violentemente la superficie bagnata, sottrae alla stessa vapor d’acqua in misura proporzionale alla differenza di pressione parziale di vapore, ma il calore latente di vaporizzazione non viene fornito alla garza dall’interno bensì dall’aria stessa, che quindi si raffredda. Si raggiunge così una situazione di regime nella quale l’aria fornisce al termometro la quantità di calore necessaria e sufficiente a far vaporizzare la quantità d’acqua evaporabile: tale situazione permane fino a che vi è acqua sufficiente nella garza che avvolge il termometro; quest’ultimo misura una temperatura inferiore a quella dell’aria che investe lo strumento, temperatura che viene detta di bulbo umido ed indicata con TB.
L’accoppiamento entro un unico strumento di due termometri, uno dei quali attrezzato con la garza bagnata, lambiti entrambi dall’aria per convezione forzata e schermati contro l’irraggiamento termico, dà origine ad uno strumento di misura capace di rilevare ad un tempo TA e TB.
Attraverso questo strumento si è riusciti a creare i diagrammi di benessere per fare fronte al problema di individuare, da un lato, le condizioni ambientali, di vestiario e di attività che consentono di conseguire la neutralità, dall’altro, la possibilità di associare ad altre condizioni fisiologiche, di vestiario ed ambientali, una scala di valutazione del grado di scostamento rispetto alla condizione di benessere. Entrambi i problemi possono essere risolti solo facendo ricorso ad indagini di carattere statistico. Perciò l'ASHRAE si è posta il problema di definire un indice capace di valutare lo scostamento dalla condizione di benessere, mentre il Fanger individua possibili combinazioni dei diversi parametri caratterizzate dal produrre tutte un ugual stato di benessere, quindi, per ogni condizione di "non benessere" valuta statisticamente la percentuale di individui non soddisfatti.
Il meccanismo della sudorazione svolge per l’individuo una funzione termoregolatrice molto importante e in esso lo è altrettanto il grado di bagnatura W. A ciascun valore di tale parametro si può pensare di associare un grado di benessere che parte dal vero benessere per W=0 per allontanarsi sempre più da tale condizione man mano che W cresce: quanto sopra è stato fatto dall’ASHRAE che, dopo aver tracciato sul diagramma psicrometrico le linee a W=cost., si è posta il duplice problema di associare ad ogni retta un valore numerico di facile comprensione e quindi di collegare la scala numerica così ottenuta ad una scala qualitativa delle sensazioni. Il primo risultato è stato conseguito attribuendo a ciascuna retta a W=cost. il valore della temperatura di bulbo asciutto corrispondente all’intersezione della stessa retta con la linea a umidità relativa costante ed uguale al 50% che ha dato origine alla scala della temperatura equivalente standard, usualmente abbreviata in TES. L’andamento delle linee di temperatura efficace standard trova piena corrispondenza con quelle che sono considerazioni quotidiane: per valori della temperatura prossimi alla neutralità il corpo umano scambia calore essenzialmente per convezione e irraggiamento, l’evaporazione è nulla o modesta e pertanto l’umidità relativa è poco influente: in effetti le rette TES sono quasi parallele, in tale zona, a quelle della temperatura dell’aria.
L’area più prossima alla linea TES=25°C rappresenta la zona di neutralità termica e può essere considerata come zona di benessere termico; questa condizione viene estesa a comprendere anche le due aree che la affiancano e che corrispondono a sensazioni termiche di leggero caldo e freddo. Temperature efficaci inferiori a 13°C e superiori a 36°C corrispondono a sensazioni di disagio. L’area al di sopra della linea W=1 comprende poi situazioni microclimatiche tollerabili solo per brevi periodi di tempo. Tale scala di temperature efficaci così ottenuta è rappresentativa per individui in attività sedentaria (1 met) e vestiti con abiti leggeri, bassa velocità dell’aria, temperatura delle pareti prossima a quella dell’aria (TA=TMR). Il diagramma ASHRAE vale però solo in condizioni moderate; esso infatti è stato definito in base alla persona media, quella cioè che lavora in ufficio, ed è adatto quindi a regolare un edificio destinato ad uffici. La temperatura è stata ipotizzata pari a 25°C, criticata da alcuni così come il diagramma stesso perché tale temperatura sarebbe troppo elevata per un ufficio.
E’ mantenuto sempre tale, sarà infatti compito del committente attribuire di volta in volta un valore alla TES (che deriva sia dalla temperatura che dall’umidità e rappresenta teoricamente anche una valutazione qualitativa, cioè un’uguale sensazione termica) da considerare nel diagramma. Le esatte condizioni di comfort non saranno mai conseguite appieno, a meno che non ci si allontani troppo dalle stesse e quindi le persone non siano troppo insoddisfatte.
Riporto i valori che sono stati ricavati sul diagramma psicrometrico. Ad ogni livello metabolico corrisponde un fascio di rette, che sembrano tutte provenire da un unico punto, dopo aver fissato la temperatura dell’aria TA (che consideriamo TO) in ascissa e il titolo x in ordinata. La prima di queste rette non è perfettamente verticale, infatti il parametro W parte da 0.06 e può arrivare al valore massimo pari a 1, per cui le corrispondenti temperature di bulbo bagnato vanno da 25°C a 35°C. Dalla pendenza del fascio si nota come la situazione di comfort a temperature poco elevate dipende quasi esclusivamente dalla sola temperatura.
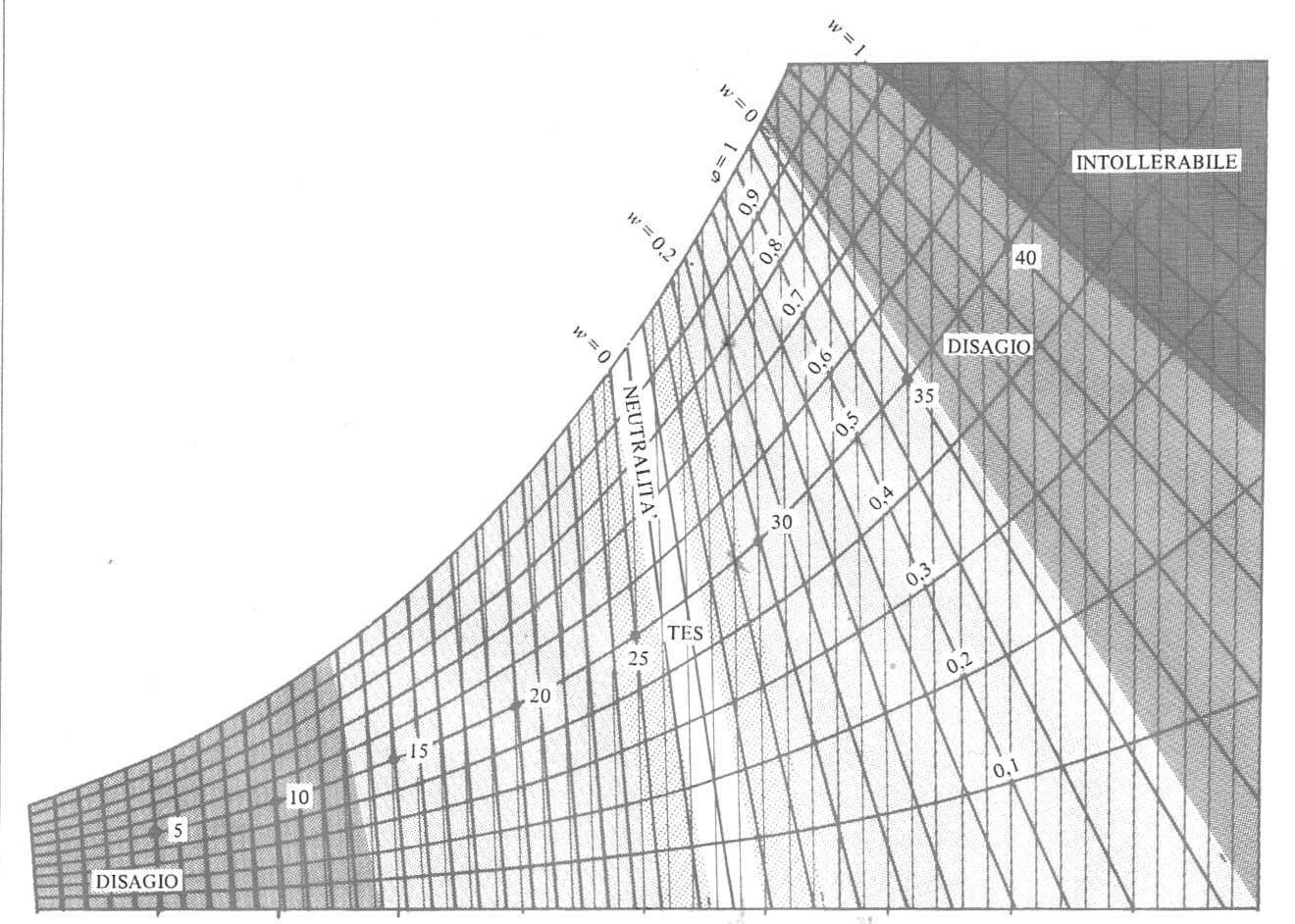
0 5 10 15 20 25 30 35 40 45 50
tA (°C)
Figura 3- Diagramma psicrometrico con sovrapposte rette a grado di bagnatura costante (W), valutate anche in termini di temperatura equivalente standard (TES), e zone caratterizzate da ugual sensazione termica.
Condizioni di benessere termico secondo il criterio di Fanger:
Per far fronte ai problemi di comfort è stato inventato dal professor Fanger, docente dell’Università di Copenaghen, il fangherometro, che misura le condizioni di comfort e discomfort. La base dell’approccio non è stata scientifico – matematica ma è stato svolto secondo test soggettivi, cioè su una base di circa 1500 studenti messi in una camera climatica e ciascuno con vestiti e condizioni di movimento e attività diverse; la validità della teoria di Fanger è quindi ristretta ad un ben definito campo di soggetti, il cui livello di attività non supera i 175 W/m2. Confrontando i risultati ottenuti in esperimenti su individui statunitensi e danesi sottoposti alle stesse condizioni termoigrometriche è stato visto che, per lo meno nelle zone temperate, non vi sono significative differenze tra le sensazioni termiche provate, per cui sembra possibile affermare che la nazionalità e la collocazione geografica, insieme con il sesso, l’età, la costituzione corporea, le differenze etniche, il ritmo cardiaco, non influenzano apprezzabilmente le sensazioni termiche.
Il metodo di Fanger permette, per ogni tipo di abbigliamento (clo) e di attività (W/m2), di calcolare le combinazioni di temperatura nell’aria (°C) e velocità relativa (m/s) che realizzano il benessere termico per persone in condizioni di regime stazionario. Nell’esperimento sono state imposte la temperatura media radiante (tMR) delle pareti della camera climatica, la temperatura media dell’aria (tA), un ventilatore che facesse variare la velocità dell’aria, il grado igrometrico (j ). Fanger poteva regolare la velocità dell’aria che usciva dal ventilatore e quindi anche il grado igrometrico man mano che le persone si sedevano di fronte al getto d’aria e davano la loro impressione sulle sensazioni che provavano grazie ai voti dati in base a una scala che oscillava tra –1 e +1 (0=benessere, -1=disagio per il troppo freddo, +1=disagio per il troppo caldo).
Facendo una media dei voti (MV, che significa appunto media vote), dati quindi sulla base delle varie condizioni termoigrometriche, questo voto medio viene chiamato PMV (voto medio previsto; per PMV pari a zero si hanno condizioni di comfort, per valori diversi dallo zero si hanno condizioni di discomfort), risultato teorico che può essere associato, sempre su base statistica, alla percentuale di individui insoddisfatti PPD. Si verifica così che nelle migliori condizioni, che corrispondono a quelle che i più considerano il benessere, la percentuale di risposte positive non supera il 95% del totale, il che significa che è illusorio realizzare la soddisfazione del 100% degli individui. Pertanto se –0.5<PMV<+0.5 allora PPD<10%, cioè meno del 10% degli individui è insoddisfatto delle condizioni termoigrometriche.
E’ possibile determinare le condizioni di benessere secondo il criterio di Fanger, utilizzando una serie di diagrammi. Le curve tracciate su di essi definiscono il luogo dei punti corrispondenti a condizioni di benessere; conseguentemente esse possono venire utilizzate per determinare il valore di un parametro fissati che siano i rimanenti. Questi diagrammi non forniscono però indicazioni per condizioni che si discostano, anche di poco, da quelle di benessere; infatti Fanger ha imposto dei limiti, dedotti sperimentalmente, ai valori della temperatura cutanea e del calore disperso per evaporazione, limiti che corrispondono alle condizioni di benessere termico. Uno di questi diagrammi è il seguente, che indica le diverse combinazioni di livello di attività, valore ICL, velocità relativa, umidità e temperatura ambiente, che consentono di ottenere il benessere ottimale, quando la temperatura media radiante, posta uguale a quella di bulbo bagnato, è uguale alla temperatura dell’aria o di bulbo asciutto:
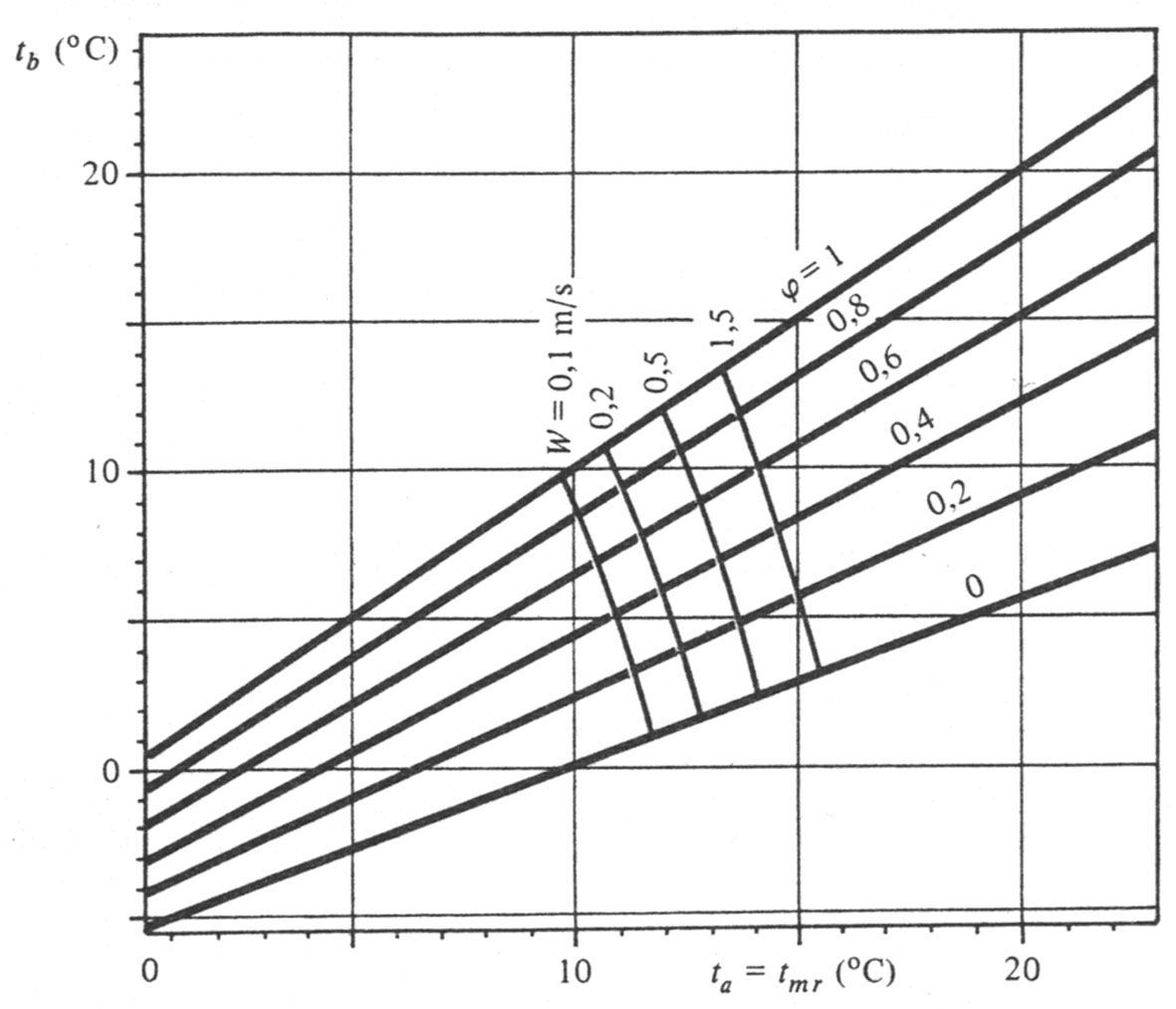
Figura 4- Correlazione tra la temperatura ambiente, assunta uguale a quella media radiante, e la temperatura a bulbo umido o il grado igrometrico, per ottenere condizioni di benessere, al variare della velocità relativa dell’aria. Attività media (2met) e corpo pesantemente vestito (1.5 clo); FCL=1.2.
Per il progettista, è molto utile poter tradurre quanto sopra esposto in un unico diagramma che consenta di valutare gli scostamenti dei parametri ambientali dai valori di benessere, in relazione al grado di soddisfacimento richiesto. Stabilito (secondo la norma ISO 7730/84 presente in Europa nei capitolati d’appalto dei requisiti dell’edificio) di accettare una percentuale di insoddisfatti pari al 10% delle persone esposte, cui corrisponde dunque un PMV di ± 0.5, ne deriva il grafico riportato in figura 5, che consente appunto di determinare lo scostamento ammissibile per la temperatura operante rispetto al valore di benessere, riportato in ordinate.
ABBIGLIAMENTI TIPICI PER ATTIVITA’ SEDENTARIE ALL’INTERNO DI LOCALI
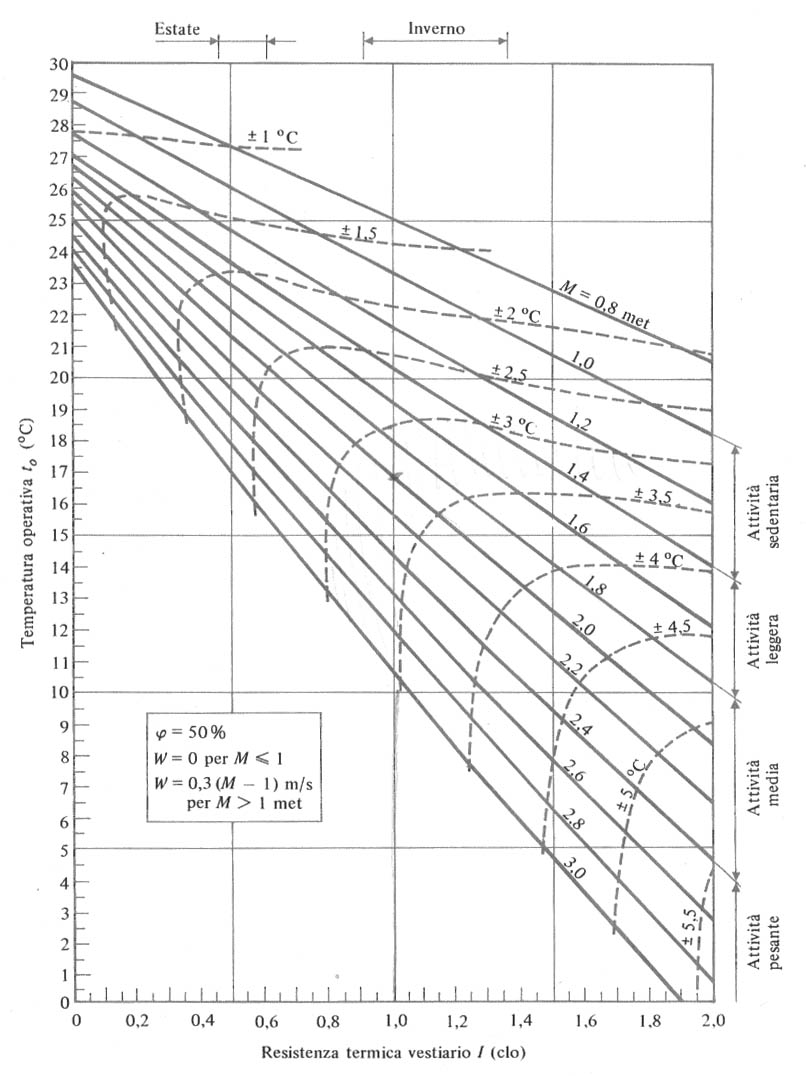
Figura 5- Diagramma del benessere termico, tracciato secondo la teoria di Fanger. Le curve a tratto continuo rappresentano le condizioni ottimali di benessere; quelle tratteggiate indicano lo scostamento possibile della temperatura operativa dal valore ottimale nella zona accettabile per il benessere (-0.5 £ PMV £ +0.5).
Tale diagramma può essere ritenuto di interesse generale anche se in realtà è limitato dai valori j =0.5, W=0 ed U=0, essendo questi usati all’interno degli ambienti confinati adibiti a funzioni abitative o terziarie. Nell’ordinata di destra di esso sono riportati i vari tipi di attività, da quella sedentaria in alto a quella pesante in basso, così che al loro crescere, e a quello del metabolismo, le curve scendono diminuendo quindi la temperatura operativa tO (°C) presente nell’ordinata di sinistra. In ascissa è riportata la resistenza termica del vestiario ICL (clo); le rette disegnate con un tratteggio sono le equivalenti delle rette a TES costante e rappresentano la situazione di comfort in funzione del grado di vestimento e dell’attività fisica.
Fissati un valore di metabolismo MET=2 e un grado di vestiario CLO=1, si vuole verificare se tali condizioni di comfort sono previste dalla norma ISO 7730/84 suddetta. Si utilizza il grafico psicrometrico per trasformare la temperatura operante TO pari a 31°C con j =0.8 nel corrispondente valore standard per l’utilizzo del diagramma j =0.5. Ne risulta una temperatura pari a 34°C, che non mi soddisfa la condizione. Si prova allora con TO=21°C e j =0.8; si ottiene TO=21.3°C con j =0.5, valore che si può accettare poiché si trova sul margine di tolleranza.
Fissando MET=1 e CLO=0.5 (cioè persone con abbigliamento estivo) si vuole sapere se una temperatura operante pari a 21°C con j =0.8 è sufficiente. Si trova che essa non va bene, infatti la temperatura operante dovrebbe essere pari a 25.5°C. La tolleranza però in questo caso è bassa (1.5°C) perché con essa lo è anche il grado di vestimento.