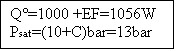TESINA
DI FISICA TECNICA
TESINA
DI FISICA TECNICA
Allieva:Saccani
Francesca
n.matricola:138772
lezione del 17/01/2002-ore:16:30-18:30
ESERCIZIO N.1: tratto dall’esame del 7/12/2001
argomento:il
moto dei fluidi
DATI
E QUESITI :
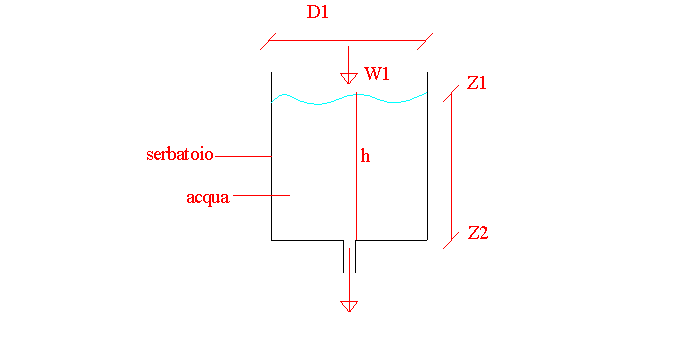
D1=diametro del serbatoio
D2=diametro dell’apertura in basso al serbatoio
H=profondità
W=velocità
R=perdita
Z1,z2=quote delle due sezioni?
?=tempo necessario all’intero svuotamento del serbatoio
T=tempo
b=coefficiente della perdita di carico concentrata nel foro

?=velocità iniziale dell’acqua(all’inizio del processo)
?=tempo necessario all’intero svuotamento del serbatoio
-1-
lezione del 17/01/2002-ore 16.30-18.30
Rispondiamo al primo quesito ricordando l’equazione di
Bernoulli per la conservazione dell’energia.
(w2![]() -w1
-w1![]() )/2+g(z2-z1)+(p2-p1)/racqua +R=0
)/2+g(z2-z1)+(p2-p1)/racqua +R=0
Poiché però questo problema è sul moto dei
fluidi non valgono le regole per
d’idrostatica;inoltre w1diventa
trascurabile rispetto alla velocitàall’imbocco.L’equazione diventa quindi
di questa forma:
w2![]()
![]() /2-gH
/2-gH
ricordiamo poi che R=b´w2/2
quindi:
w2=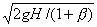 =
= 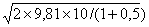 =11,43m/s
=11,43m/s
Ora rispondiamo alla seconda domanda che non è così
semplice perché la velocità di svuotamento del serbatoio non è costante durante
la fuoriuscita .Ricordando la relazione del tubo di Venturi:
w1´A1=w2A2 Þ W1´p´D1![]() /4=w2´p´ D2
/4=w2´p´ D2![]() /4 Þ w1=w2(D2/D1)
/4 Þ w1=w2(D2/D1) ![]()
w2=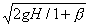 Þ w2=
Þ w2=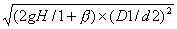 =dh/dt=dt=
=dh/dt=dt= =
=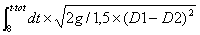 Þ
Þ
![]() Þ t tot´
Þ t tot´![]() ==
== ![]() ´0,5/0,5=2´
´0,5/0,5=2´![]() Þ t tot = 2´
Þ t tot = 2´![]() /
/![]() ´ (D2
´ (D2![]() /D1
/D1![]() ) =
) =
=2![]() /
/ ![]() ´(1/625)=1.093 s
´(1/625)=1.093 s
ESERCIZIO N.2:
Tratto dall’esame del 07/12/2001
DATI E QUESITI:
Q°=potenza della
resistenza
Psat=pressione del
vapore saturo contenuto
Mvap=portata in massa del vapore
Tsat=temperatura di saturazione
Q=calore
-2-
lezione del 17/02/2002-ore 16.30-18.30
?=temperatura di saturazione
?=Mvap
Per rispondere alla prima domanda è sufficiente
guardare il valore corrispondente sulla
tabella alla pressione 13bar.
Tsat=191°C
Per rispondere
alla seconda domanda devo conoscere il calore latente di vaporizzazione poiché
questo è il processo in questione.Tale valore lo trovo facilmente sulle
tabelle Þ r =1976kJ
Vediamo cosa
succede nel nostro processo:la potenza di 1056W che ho a disposizione
corrisponde a 1056J/s.Quindi la potenza in un secondo equivale a 1056 J.
R =1976 Kj/Kg = Q/M =1056/M Þ 1056/1.976.000=0,534Kg/s
Quindi ogni secondo ½ gr d’acqua vaporizza per mezzo del calore.
ESERCIZIO N.3:
Problema sui tubi di pitot tratto dall’esame dello
07/12/2001
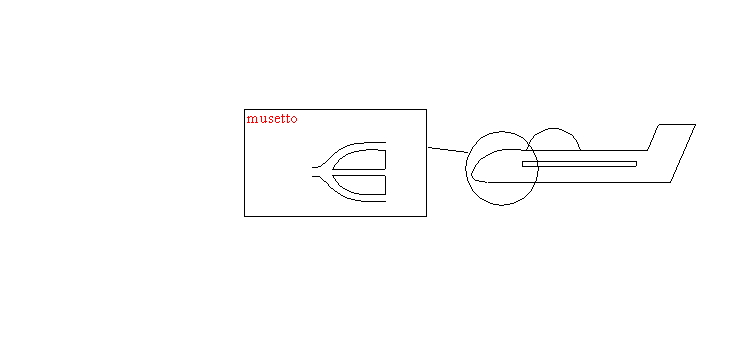
DATI E QUESITI:
u=velocità dell’aereo
Dp=pressione differenziale
pR=pressione di ristagno
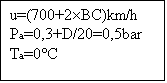
?=Dp ?=pR
Sul musetto dell’aereo è stato montato un tubo di
pitot.Applichiamo l’equazione di Bernoullidel tubo di Pitot.
-3-
Lezione del 17/02/2002-ore 16.30-18.30
(u2![]() -u1
-u1![]() )/2+g´(z1-z2)+(p1-p2)/raria+R=0
)/2+g´(z1-z2)+(p1-p2)/raria+R=0
Sappiamo però che u1 non c’è perché in 1 l’aria
è ferma e u2 è la velocità dell’aereo;inoltre z2-z1 viene
eliminato perché non c’è differenza di moto dato che il moto dell’aereo è
considerato orizzontale.Le perdite poi vengono trascurate per le piccole
dimensioni del tubo e l’alta velocità dell’aereo.
U2![]() /2=Dp/raria Þ Dp=raria´u2
/2=Dp/raria Þ Dp=raria´u2![]() /2
/2
L’aereo vola a 0°C ed a una pressione alta;quindi la
densità dell’aria è ben diversa da quella che abbiamo noi.
La densità è il reciproco del volume specifico:
pv=RT Þ p/r=R Þ r=p/RT=50.000/287.273=0,6381Kg/m
ora risostituisco il valore trovato: Dp=raria´u2![]() /2=0,6381 Kg/m
/2=0,6381 Kg/m![]()
ora dobbiamo trasformare la velocità dell’aereo in m/s (il
fattore di scala è :1km/h=1000/3600 m/s)
h=746´1000/3600=207,22m/s
a questo punto riesco a trovare Dp Þ Dp=0,6381´ 207,22![]() /2=13071,5 Pa
/2=13071,5 Pa
da qui posso poi ricavare Pr=Pstat+Dp Þ pr=500.000+13071,5=63701,5Pa
ESERCIZIO N.4:
problema tratto dal compito del 26/09/2001
DATI E QUESITI:
H=entalpia totale
P=pressione
T=temperatura
pv=volume specifico
h=entalpia specifica

?=determinare peso e volume di una massa di aria
L’aria è un gas perfetto.Scriviamo quindi l’equazione di
stato dei gas perfetti Þ pv=MRT
Possiamo dividere per l’unità di massa Þ Pv=RT Þ da qui
riesco a ricavare il volume specifico.
V=RT/p = 287´(106+273)/600.000=0,1813m![]() /kg
/kg
Non ho la massa ma conosco l’entalpia totale:
H=M´h Þ sappiamo
che h=cp´t (cp rappresenta il calore specifico a pressione
costante)
Quindi posso scrivere H come
H=M´cp´t Þ M=H/cp´t=143.000/1.000´106=1,284kg
Da qui ricavo il volume totale:
V=M´v Þ1,284´0,181=0,2329
m![]()
Ora non mi resta che moltiplicare la massa per
l’accellerazione di gravità per trovare il peso.
P=M´g=1,284´9,81=12,60N
-4-
lezione del 17/01/2002-ore 16.30-18.30
ESERCIZIO
N.5:
Problema tratto dal compito del 29/06/2001

DATI E QUESITI:
D=diametro
Qm=portata in massa
W=velocità
Dp=salto di pressione
b=coeff.della perdita di carico concentrata in funzione
della geometria del tubo
R=perdita di carico concentrata

?=R ?=b
Per prima cosa scriviamo l’equazione di bilancio delle due
sezioni utilizzando l’equazione di Bernoulli.
-W2![]() -w1
-w1![]() /2+g(z2-z1)+p2-p1/r+R=0
/2+g(z2-z1)+p2-p1/r+R=0
Il primo membro dell’equazione possiamo eliminarlo perché
le due velocità sono uguali(il diametro in un tubo è sempre lo stesso infatti)e
pure la differenza di quota perché il tubo giace su un piano orizzontale.
L’equazione quindi risulta:
p2-p1/r+R=0
Poiché sappiamo che la perdita può essere scritta come:R=b´w![]() /2
/2
Dp/r=b´w/2 (w indica la velocità media del fluido)
+ precisam.
Per ricavare w utilizziamo la formula di portata di
calore Þ Qm=r´w´A Þ Qm=r´w´p´D![]() /4
/4
W=Qm´4/r´p´D![]() =0,5´4/1000p´0,023=1,20m/s
=0,5´4/1000p´0,023=1,20m/s
-5-
lezione del 17/02/2002-ore 16.30-18.30
Mi accorgo poi che i dati per trovare R ce li ho:R =Dr/r
(entrambi noti nel problema)
-R=7000Pa/1000=7
J/kg
Avendo poi trovato w,posso determinare anche b.
b=7,2/(1,20)![]() =9,`6
=9,`6
ESERCIZIO N.6:
Problema tratto dall’esame del 26/06/01
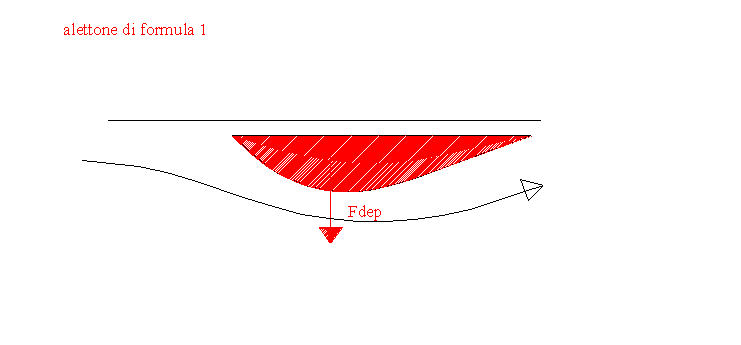
DATI E QUESITI :
Fdep=spinta deportante
U1=velocità dell’automobile
U2=velocità dell’aria sotto l’alettone
S=superficie dell’alettone
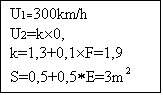
?=Fdep
Notiamo che sotto l’alettone la pressione è minore per
l’aumento della velocità.(di k volte)
P2Ð P1
Usiamo quindi
l’equazione di Bernoulli:
meglio
u1![]() /2+p1/raria=u2
/2+p1/raria=u2![]() /2+p2/raria Þ p1-p2=raria´u2
/2+p2/raria Þ p1-p2=raria´u2![]() -u1
-u1![]() /2 (1)
/2 (1)
u1=300kg/h´1000/3600=83,33m/s
u2 è maggiore perché è = u1´k
quindi possiamo immediatamente scrivere u2=1,9´83,33=158,33m/s
Ora posso calcolare Dp,sapendo che raria =1,2kg/m
-6-
lezione del 17/02/2002-ore 16.30-18.30
Dalla relazione (1) scritta sopra ricavo:
p1-p2=1,2´[158,33![]() -83,33
-83,33![]() /2]=10.784Pa
/2]=10.784Pa
da qui:
Fdep=Dp´S=10.784´3m![]() =32.353N
=32.353N
![]()
![]()
-7-