Giacomo Ribolla, mat. 133187 data
17-01-2002 ore 16.30 / 18.30
Esercitazioni d’esame
Esame del 7-12-2001: esercizio 1 2 3
Esame del 29-6-2001: esercizio 1 2 3
Consigli per una giusta
lettura dei dati e Consigli per l’uso delle
griglie excel.
Esercizio
n 1 esame del 7-12-2001
In un recipiente cilindrico è contenuta acqua. Il recipiente ha un diametro D1 pari ad 1+0.02*CD m, e un’altezza H pari a 5+E m. L’acqua esce da un foro (b =0.5) a sezione circolare di diametro D2 = 1/25 D2. Determinare la velocità iniziale di fuori uscita dell’acqua e il tempo necessario per lo svuotamento.
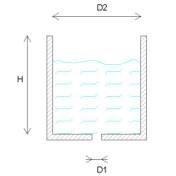
Consigli:
per svolgere questo esercizio è necessaria la conoscenza della teoria riportate nelle tesine 20- l’equazione di Bernoulli- e 21- calcolo delle perdite di carico-.
Svolgimento:
utilizzo l’equazione di Bernoulli, scegliendo la prima sezione a pelo libero dell’acqua e la seconda all’imboccatura del foro.
![]()
for.1
osservo che: L= nullo; W1 è trascurabile rispetto a W2; non c’è differenza di pressioni DP= 0
ottengo perciò:
![]()
for.2
da cui:
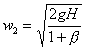
for.3
poiché:
![]()
OSSERVAZIONE: è più corretto sostituire ed H, la variabile h che va da H…0, poiché la velocità non è costante ma diminuisce in proporzione all’altezza.
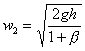
for.4
per l’equazione di continuità so che
W1A1= W2A2
for.5
da for.5 e for4 ottengo
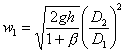
for.6
usando la legge del moto del pelo libero
![]()
for.7
sostituendo a W1 la for6 e svolgendo le opportune semplificazioni ottengo:
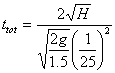
for.8
Griglia excel per verifica risultati.
Esercizio n 2 esame del 7-12-2001
 In
una caldaia per la produzione di vapore,una resistenza genera calore per effetto joule. La potenza
generata è pari a P = 1000+EF Watt. La
caldaia contiene acqua satura aPsat =10+C bar. Determinare Tsat
e QM vap.
In
una caldaia per la produzione di vapore,una resistenza genera calore per effetto joule. La potenza
generata è pari a P = 1000+EF Watt. La
caldaia contiene acqua satura aPsat =10+C bar. Determinare Tsat
e QM vap.
Consigli:
per svolgere questo esercizio è necessaria la conoscenza globale dalla termodinamica
Svolgimento:
la Tsat si trova sulle tabelle.
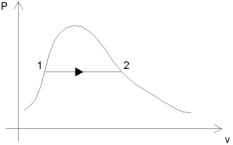 Analisi grafica della trasformazione.
Analisi grafica della trasformazione.
Il calore necessario Q = r calore latente di vaporizzazione per kg; r è tabellato.
La potenza è uguale a:
![]()
da cui ottengo:
![]()
in questo esercizio non è fornita nessuna griglia excel per le soluzioni; riportiamo un esempio numerico:
mat: 123456
P = 1056 Watt
Psat = 13 bar
Dalla tabelle ottengo: Tsat = 191°C r = 1976 kJ/kg
Seguendo le formule ottengo QM = 0.534 g/s
Esercizio n 3 esame del 7-12-2001
Un aereo vola a velocità u= 700+2*BC km/h, a una quota tale per cui la pressione è P = 0.3+ D/20 bar e la temperatura è Ta = 0°C. sul muso dell’aereo è montato un tubo di Pitot, determinare la pressione differenziale DP e la pressione di ristagno Pr

Consigli:
per svolgere questo esercizio è necessaria la conoscenza della teoria riportate nelle tesine n 22 – metodi di misurazione fluido dinamici-.
Svolgimento:
da Bernoulli, sapendo che L =0; u1 =0; e che Z1-Z2 =0 e chiamando P2 -P1 = DP; ottengo
![]()
![]()
for.1
OSSERVAZIONE: non posso usare il r dell’aria normale perché la pressione è più bassa ma lo devo calcolare in funzione di P e di T , poiché
Pv =
Rt
![]()
Calcolo r. Sostituendo nelle for.1 u e r ottengo DP
Pr lo calcolo sapendo che
PR = P - DP
Griglia excel per verifica risultati.
Esercizio n 1 esame del 29-06-2001
Determinare il peso e il volume di una massa d’aria di pressione P = 2+D bar; temperatura T = 50+EF °C e entalpia H = 120+BC kJ
Consigli:
per svolgere questo esercizio è necessaria la conoscenza della teoria riportate nelle tesine 5 - gas perfetti-.
Svolgimento:
uso equazione di stato dei gas perfetti
Pv = RT
Da cui ottengo v. So poi che
H = M h =M cp T
cp = 1000, otteno così la massa M con la quale posso calcolare volume e Peso
V = M v
P = M g
g = 9.81 N
Griglia excel per verifica risultati.
Esercizio n 2 esame del 29-06-2001
Determinare la perdita di carico R e il coefficiente di perdita di carico localizzato
b causati da un filtro, sapendo che DP = 0.03+0.01*D bar, e D1 = 20+C mm. E portata in massa QM =0.3+0.05*d kg/s.

Consigli:
per svolgere questo esercizio è necessaria la conoscenza della teoria riportate nelle tesine 20- l’equazione di Bernoulli- e 21- calcolo delle perdite di carico-.
Svolgimento:
si deve usare l’equazione di Bernoulli tenendo conto che il Dw DH sono nulli.
![]()
for.1
sapendo che
P1-P2 =DP
rh2o = 1000
calcolo R
![]()
posso calcolare poi la velocità W:
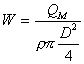
for.2
e il b:
![]()
![]()
Griglia excel per verifica risultati.
Esercizio
n 3 esame del 29-06-2001
Un alettone da formula 1 da luogo ad un valore medio della velocità dell’aria sulla sua faccia inferiore più elevato di un fattore (k =1.3+0.1*F) rispetto alla velocità della vettura (300 km/h), mentre sulla sua faccia superiore, piana, si suppone che la velocità dell’aria coincida con quella della vettura. Conoscendo la superficie dell’alettone (S =0.5+0.5*E), determinare la spinta deportante da esso prodotta.
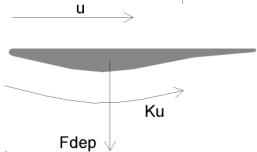
Consigli:
per svolgere questo esercizio è necessaria la conoscenza della teoria riportate nelle tesine 23 - il moto esterno-.
Svolgimento:
uso Bernoulli, poiché sotto l’alettone c’è un aumento della velocità, la pressione diminuisce
![]()
![]()
![]()
dove u1= 300km/h = 83.33 m/s e u2 = ku1
ottenutoDP calcolo la Fdep
Fdep = DP S
Griglia excel per verifica risultati.
Consigli per una giusta lettura dei dati
Siricorda che le cifre in lettere: A B C D E F dei dati si riferiscono rispettivamente al primo, secondo, terzo, quarto, quinto e sesto numero di matricola.
Es. mat: 567845 allora A =5; B =6; C =7; D =8; E =4; F =5.
A + B indica la somma es: 5+6 =11
A * B indica il prodotto es: 5*6 =30
A / B indica la divisione es: 5/6 = 0.833
Mentre la scritta AB va letta semplicemente come 56
Consigli
per l’uso delle griglie excel
Bisogna inserire il n di matricola nella colonna B ognuno nell’apposito spazio. Esempio, 1 es dell’esame del 29-06-2001:
la griglia è: se la mat: è 123456 inserisco cosi


i risultati saranno modificati di conseguenza.