Pizzuti Luigi
Matricola 141465
Lezione del 17/01/2002
Luigi Pizzuti presenta:”Storia di un ordinario studente…”
…C’
era una volta,all’Università di Parma uno studente che ogni
giorno con la sua “spider”si recava
alle lezioni di 
fisica tecnica del temibile prof Angelo
Farina…
![]()

…ma
come è noto gli studenti
si distraggono facilmente,ed hanno
numerosi hobby….
![]()

…e
si” dimenticano” di fare gli
esercizi di fisica
tecnica….
Ma un brutto giorno,il nostro simpatico amico “studente ordinario”
Dovette mettere da parte i suoi hobby e fare il compito di fisica tecnica
All’ora stabilita consegnò

 Un
voluminoso pacco di fogli,ma
Un
voluminoso pacco di fogli,ma
Purtroppo…
erano vuoti!!!!!!!!

…morale della favola:
volete passare l’esame di
fisica tecnica?
…non trascurate i vostri
hobby ma fate gli esercizi!!!!!!!!!!
1° Esercizio –
Fluidodinamica (tolleranza +/- 10%)
In un recipiente cilindrico è contenuta acqua. Il recipiente ha un diametro D1 pari ad 1+0.2*CD m ed un’altezza H pari a 5+E m. L’acqua esce attraverso un foro a sezione circolare, avente diametro D2 pari a 1/25 D1. Il coeff. b del foro di uscita vale 0.5. Determinare:
- Velocità iniziale di uscita dell’acqua (m/s)
- Tempo che impiega il serbatoio
a svuotarsi (s)
SVOLGIMENTO ESERCIZIO
(Si
riportano a scopo esemplificativo i dati utilizzati dal prof.)
sez1
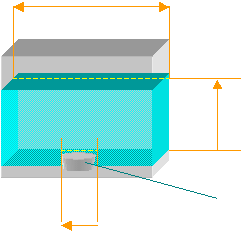
![]() D1=1.68m
D1=1.68m
D2=1/25*1.68=0.0672m
H
H=10m
Sez2
b =0.5
![]()
A questo punto,possiamo
impostare il procedimento di risoluzione,utilizzando l’equazione di Bernoulli;chiaramente le due sezioni da
considerare nell’equazione dovranno essere tali da facilitare il calcolo ovvero
devo scegliere “intelligentemente”2 sezioni dove si annulleranno il maggior
numero possibile di termini:
SEZ1:consideriamo la sez al
pelo libero del serbatoio
SEZ2:consideriamo la sez
allo sbocco di uscita
Con la scelta di queste due
sezioni ottengo che nell’eq di Bernulli il salto di pressione si annulla poiché
entrambe le sez sono a contatto con l’aria
(W22
–W12) /2 + g(z2
– z1 ) +(P2 –P1 )/j +R = O
![]()
questo termine si annulla
in quanto tra le due sez scelte
non esiste alcun salto di pressione
poiché entrambe sono a contatto
con l’aria!
Inoltre il termine w12
diventa trascurabile rispetto la velocità di fuoriuscita nella sez
all’imbocco!Infine si ricorda che R=b w22/2
Questa era l’impostazione
corretta dell’equazione ,da cui:
![]()
![]() ____________
____________
![]() w22 /2 – g*H +b w22 /2
da cui w2= 2gH/
1+b = 11,43 m/s
w22 /2 – g*H +b w22 /2
da cui w2= 2gH/
1+b = 11,43 m/s
Adesso possiamo procedere
nel calcolo del tempo impiegato dal serbatoio nello svuotarsi,e in questo
passaggio risiede la difficoltà maggiore poiché sappiamo la velocità di
fuoriuscita iniziale ma tale velocità nello svuotarsi decresce in quanto la
pressione dell’acqua soprastante diminuisce gradualmente!Quindi ci occorre
trovare un valore di velocità”media”:
w1*A1=
w2*A2 ovvero w1*PD12 /4 = w2*PD22 /4
![]()
![]() w1= 2Gh *(D2/D1)2
= -dh/dt poichè la vel è la derivata
del dist/tempo
w1= 2Gh *(D2/D1)2
= -dh/dt poichè la vel è la derivata
del dist/tempo
![]()
![]()
![]()
![]()
![]()
![]() t tot Æ
t tot Æ
![]() dt 2g/1,5 *
(D2/D1)2 = - h-0.5 dh
dt 2g/1,5 *
(D2/D1)2 = - h-0.5 dh
![]()
![]()
![]() 0 H
0 H

![]()
t
tot* 2g/1,5 (D22/D12)
= h0.5/0.5 =
2 H
![]()
2
H
![]() T
tot =
= 1093 s
T
tot =
= 1093 s
![]()
2g/1,5 (D1/D2)
2° Esercizio –
Termodinamica (tolleranza +/- 5%)
Determinare peso e volume di una massa di aria di assegnata pressione, temperatura ed entalpia.
|
Pressione |
P = 2+D
=
bar |
|
Temperatura |
V = 50 + EF
= °C |
|
Entalpia |
H = 120+BC = kJ |
- Peso N ?- Volume
M![]() ?
?
SVOLGIMENTO ESERCIZIO
La difficoltà di questo esercizio consiste nel riuscire a impostare semplici equazioni coi dati ricevuti per poter arrivare a conoscere il peso e il volume.
Riportiamo come esempio i
dati utilizzati dal prof:
p=6 bar
T=106°C con questi dati posso
ricavare il volume specifico:
H=143Kj p*v=R*T ® v=R*T/p
v=0.1813mc/Kg
![]() H=M*h ® V=M*Cp*T M=H/Cp*T
H=M*h ® V=M*Cp*T M=H/Cp*T
M=1.284Kg
V=M*v

V=0.2329
mc
P=M*g
P=12.60N
(ATTENZIONE! Il peso va espresso in
ewton,molti alunni lo scrivono in kg,
è un
errore!!!!)
3° Esercizio –
Fluidodinamica (tolleranza +/- 5%)
Determinare
la perdita di carico R ed il coefficiente di perdita di carico localizzata b prodotto da un filtro antisabbia,
conoscendo il diametro del condotto, la portata di acqua e la caduta di
pressione prodotta.
|
Diametro interno |
D = 20 + C = mm |
|
|
|
|
Portata in massa |
Qm
= 0.3+0.05*D = kg/s |
|
Caduta di pressione |
Dp = 0.03+0.01*D = bar |
- Perdita di carico R ( J/kg) ?
![]() - Coeff. di accidentalità b? filtro
- Coeff. di accidentalità b? filtro
SVOLGIMENTO ESERCIZIO
Utilizzando i dati considerati durante la lezione procediamo con
l’esempio di risoluzione:
Dp=salto di
pressione=0.07 bar
D=diametro tubo(è
costante)=23mm
Qm=portata in massa=0.50
Kg/s
Lo scopo del problema è
quello di trovare R e b lavorando con
l’equazione di Bernoulli,grazie alla
quale non occorre consultare altro materiale e tabelle varie….
Sez1 sez2
Filtro
antisabbia

Chiaramente la scelta delle
due sezioni da considerare nell’equazione dev’essere dettata dal buon
senso,ovvero cercheremo trovare il più alto numero di termini nulli o
semplificabili:
come mostra il disegno la
sez1 sarà scelta in un punto precedente il filtro mentre la sez2 chiaramente
successiva al filtro!
--Poichè la
velocità nelle due sezioni scelte è la stessa il primo termine dell’equazione
risulta nullo!
--Il tubo come
mostra il disegno è in posizione orizzontale,per cui anche il secondo termine
dell’equazione si annulla!
![]() Rimane: ( p2 - p1)/j + R = 0 R
= ( p2-p1 )/j
Rimane: ( p2 - p1)/j + R = 0 R
= ( p2-p1 )/j
R= 7 j/Kg
Ma sappiamo anche che R = b*w2/2 dove w=
velocità media
Dalla formula Qm= j*w*P D2/4 ricavo w= Qm*4/j* P D2
W= 1,2 m/s
Infine posso ora scrivere b in funzione della velocità: b =2* R/W2
b = 9,66
(ATTENZIONE:è un numero puro!!!)
4° Esercizio –
Fluidodinamica (tolleranza +/- 15%)
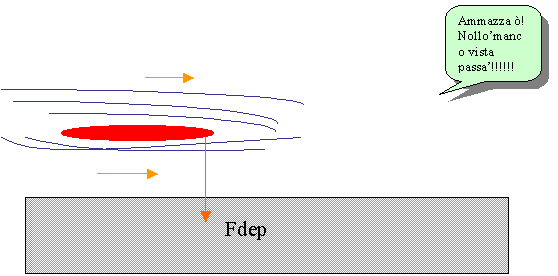
Un
alettone da formula 1 dà luogo ad un valore medio della velocità dell’aria
sulla sua faccia inferiore più elevato di un fattore k rispetto alla velocità
della vettura (300 km/h), mentre sulla sua faccia superiore, piana, si suppone
che la velocità
dell’aria
coincida con quella della vettura. Conoscendo la superficie dell’alettone,
determinare la spinta deportante da esso prodotta.
 Coefficiente di aumento di velocità K=1.3+0.1F =1.9
Coefficiente di aumento di velocità K=1.3+0.1F =1.9
![]()
![]() Superficie alettone
S=0.5+0.5E mq
Superficie alettone
S=0.5+0.5E mq
V1

V2
SVOLGIMENTO ESERCIZIO
Consideriamo a
scopo esemplificativo I dati utilizzati dal prof:
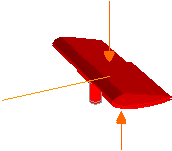
K = 1,9
S = 3 m2 Pa

![]()
![]()
![]() Pb < Pa
Pb < Pa
S
Pb
Anche in
questo esercizio il procedimento risolutivo richiede la semplice applicazione
dell’equazione di Bernoulli:
![]() v12/2
+ p1 /ja = v22 /2 + p2/ja p2 – p1
= ja* v22
– v12 / 2
v12/2
+ p1 /ja = v22 /2 + p2/ja p2 – p1
= ja* v22
– v12 / 2
p2 – p1 = 10784 Pa
A questo punto
abbiamo ciò che serve a calcolare la forza deportante:
Fdep = (p2 – p1)* S
Fdep =32353 N
5° Esercizio – Fluidodinamica (tolleranza +/- 10%)
Un aereo vola a 700+2BC Km/h
ad una quota a cui la pressione atmosferica è 0.3+D/20 = 0.5 bar(Pstat)
Sulla punta dell’aereo la
temperatura T= 0 ed è posizionato un Tubo di Pitot,calcola:
-
-
 Dp(Pr-Pstat)?
Dp(Pr-Pstat)?
-
Pr?
SVOLGIMENTO ESERCIZIO
La risoluzione di questo
esercizio prevede l’utilizzo dell’equazione di Bernoulli,nella quale si annulla il secondo termine e inoltre si
considera v1=0 poiché punto stagno;infine anche R non compare
nell’eq poiché non vi è resistenza.Riassumendo l’equazione da impostare è la
seguente:
![]() Dato v=velocità aereo v2/2+
Dp/jaria=0 Dp=jaria*v2/2
Dato v=velocità aereo v2/2+
Dp/jaria=0 Dp=jaria*v2/2

Attenzione:la densità
dell’aria all’altezza dell’aereo è minore rispetto la densità a quote basse in
cui ora noi siamo…bisogna ricavarla!
j= p/R*T = 0,631 Kg/m3
A questo punto abbiamo tutti i dati necessari per calcolare Dp=13701,5Pa
Pressione di ristagno
Pr=Pstat+Dp=63701,5 Pa