Alice Pinetti 139141

25/10/2001, 14.30 – 16.30

BILANCIO ENERGETICO DI SISTEMI

Due sistemi sono in equilibrio termico se, quando vengono posti a contatto tramite una parete diatermica (cioè che facilita l’interazione termica), le loro variabili di stato non mutano.

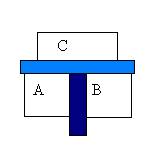
Due sistemi possono essere in equilibrio termico anche se non sono a contatto diretto:

A è in equilibrio con C e B è in equilibrio con C, quindi anche A e B sono in equilibrio tra di loro anche se sono separati da una parete adiabatica. Questa infatti impedisce ogni contatto termico.

In entrambi i casi i due sistemi A e B, essendo in equilibrio, hanno la stessa temperatura.

Il calore è l’energia scambiata tra un sistema ed il suo ambiente unicamente a causa di una differenza di temperatura che sussiste tra il sistema e qualche parte del suo ambiente.

Il termine calore è usato in modo appropriato quando si riferisce ad una quantità di energia che viene trasferita ad un sistema o da un sistema. Non si tratta di un’energia che risiede in un sistema o gli appartiene. Non si parla di “calore di un sistema” ma di “calore fornito/sottratto a un sistema”.

Tra un sistema ed il suo ambiente avviene anche uno scambio di lavoro. Il lavoro è l’energia scambiata tra un sistema e il suo ambiente attraverso meccanismi indipendenti dalla differenza di temperatura esistente tra loro.

La termodinamica considera soprattutto queste due forme di energia.

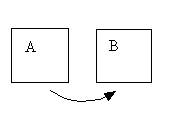
Prendiamo in considerazione per esempio un sistema allo stato iniziale A; supponiamo che vada incontro a delle trasformazioni di lavoro e calore fino a trovarsi nello stato finale B.

Nello stato A l’energia totale del sistema è , mentre allo stato B è . Tali valori, E_A ed E_B, sono uguali perché l’energia totale di un sistema è un valore costante, quindi E_B non è altro che il valore E_A dopo le trasformazioni. Da ciò consegue il 1° Principio della Termodinamica: in una trasformazione in cui la quantità di calore Q viene fornita al sistema e il lavoro L viene compiuto dal sistema, l’energia totale trasferita al sistema è pari alla variazione DU dell’energia interna al sistema stesso.

Il primo principio introduce il concetto di energia interna ed esprime la conservazione dell’energia. Tale valore non dipende dal tipo di trasformazione avvenuta nel sistema, ma dipende unicamente dallo stato finale e da quello iniziale del sistema stesso. Per questo motivo l’energia interna è una variabile di stato. Viceversa il calore e il lavoro non sono variabili di stato. La quantità di calore fornita in una trasformazione che connetta gli stati iniziale e finale dipende dal particolare modo in cui la trasformazione viene effettuata e anche il lavoro compiuto dal sistema nella trasformazione dipende dalla trasformazione stessa.

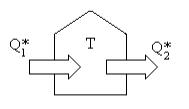
Il primo principio è importante anche per definire la quantità di calore da fornire per scaldare una casa. Una casa disperde parte del calore fornito come avviene in figura, quindi è necessario immettere più calore del necessario in modo tale che all’interno la temperatura rimanga costante. È,necessario quindi che . Nella figura sono stati indicati con le lettere Q₁* e Q₂* la quantità di calore fornito e disperso nel tempo; si parla in questo caso di potenza. La variabile fondamentale da considerare è il tempo. Per esempio i contatori presenti nelle case misurano il calore fornito in chilowattora (kWh):

cioè un’energia.

Quando si progetta un impianto si dimensiona la potenza, non l’energia. Un impianto comprende il condizionamento, la ventilazione, il riscaldamento e il raffrescamento. La ventilazione forzata è richiesta quasi ovunque e si effettua mediante cappe con estrattori motorizzati che estraggono 2 volumi/h. La portata è dunque . Nelle abitazioni si parla solitamente di sola estrazione dell’aria. Il raffrescamento consiste di impianti che rinfrescano l’aria in estate.

Le dispersioni di calore dipendono dai metri quadri di superficie e, trascurando fenomeni convettivi, tali dispersioni avvengono per conduzione ed irraggiamento. L’irraggiamento descrive ciò che avviene dalla superficie esterna del muro all’ambiente circostante. La quantità reale di calore che attraversa il muro dipende dalla sua conduzione termica.

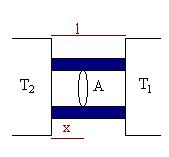
Nel processo di conduzione il calore viene trasferito tra due sistemi tramite il mezzo che li mette in comunicazione. Supponiamo che nessuna parte di questo mezzo sia in moto, cioè se si tratta di un solido è rigido e se è un fluido non presenta circolazione di correnti. Supponiamo di avere due sistemi alle temperature T₁ e T₂ (T₂>T₁). Tra essi è interposta una barra omogenea di sezione A e lunghezza l. Una parete adiabatica copre la superficie laterale della barra e impedisce qualunque flusso di calore attraverso tale superficie. Lo scambio di calore avverrà da T₂ a T₁. Supponendo che tale scambio avvenga a regime stazionario (la temperatura non cambia in nessun punto della barra) la quantità di calore Q che fluisce attraverso una sezione della barra stessa in un intervallo di tempo t è la stessa lungo tutta la barra. Quindi l’energia viene trasferita attraverso il mezzo senza che nessuna parte di esso ne acquisti o ne perda. Si definisce corrente termica C la quantità di calore che fluisce nell’unità di tempo attraverso una sezione data:

(1)

In regime stazionario C ha il medesimo valore in tutta la barra omogenea ed è:

· proporzionale alla differenza di temperatura T₂ – T₁;

· proporzionale all’area A della sezione della barra;

· inversamente proporzionale alla sua lunghezza l;

· dipendente dal materiale di cui la barra è costituita.

(2)

Il termine k è il coefficiente di conducibilità termica caratteristico del materiale di cui è fatto il mezzo, ma indipendente dalle dimensioni e dalla forma. La dipendenza del coefficiente di conducibilità termica dalla temperatura è per la maggior parte delle sostanze trascurabile.

L’unità di misura nel Sistema Internazionale (SI) della corrente termica è il watt (W) e quella del coefficiente di conducibilità termica è . Una sostanza è un buon conduttore se ha alti valori di conducibilità termica, come i metalli; viceversa bassi valori di conducibilità termica indicano che la sostanza è un buon isolante. Nell’industria delle costruzioni le proprietà isolanti dei materiali in condizioni di flusso di calore a regime stazionario vengono talvolta espresse mediante il cosiddetto “valore R”.

Applicando la relazione (2) a una lastra di spessore con una differenza positiva di temperatura tra le due facce: (3).

Ricaviamo da questa relazione DT in termini di corrente termica per unità di area : poiché , allora (4).

L’equazione (4) e il “valore R” risultano particolarmente utili nella determinazione della conduzione termica attraverso strutture stratificate di diversi materiali quali le pareti o le pavimentazioni. La differenza di temperatura tra le due facce della struttura composta è pari alla somma delle differenze di temperatura tra le facce dei singoli strati e il “valore R” efficace della struttura composta è semplicemente la somma dei “valore R” dei vari strati. Con il simbolo R viene spesso indicata anche la resistenza termica pari a e quindi uguale al “valore R” per unità di superficie.

In un sistema di unità di misura in uso nell’industria statunitense delle costruzioni, l’unità di misura dell’unità di calore è la Btu (British thermal unit) e 1Btu = 1055J. L’unità di area è il piede quadrato (ft²) e l’unità di tempo è l’ora (h).

L’unità di lunghezza per gli spessori è il pollice e la differenza di temperatura viene espressa in °F.

L’unità del “valore R”, che sia esplicitamente indicata o sottintesa, è .

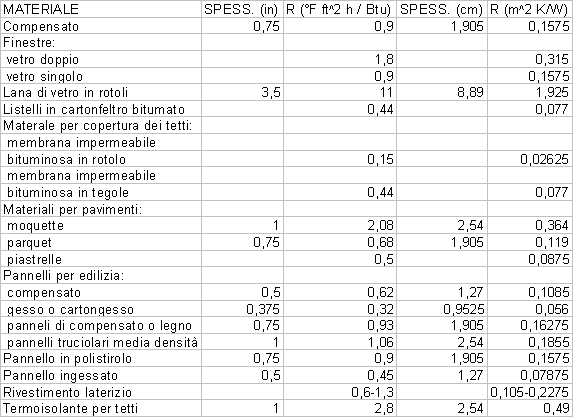
I valori forniti nella tabella corrispondono allo stesso spessore di materiale fornito prima in “in” (inch), cioè in pollici, e poi in centimetri. Il valore di un pollice è:. Anche per il “valore R” sono stati forniti due valori, il primo con unità anglosassoni e il secondo con unità SI. Il fattore di conversione è:

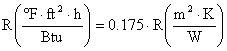
Esercizi:

1- Supponiamo di avere un edificio cubico di lato 10m sorretto da pilotis. Si vuole mantenere una temperatura interna T₁ di 20°C mentre all’esterno abbiamo una temperatura di 0°C. Su ogni parete laterale è inserita una finestra di superficie 2m². L’edificio è costruito con mattoni UNI pieni, con muri a due teste più isolante da 5cm e rivestimento esterno da 3cm (spessore totale del muro ). Poiché gli impianti domestici hanno una potenza massima istantanea di 3500W, se , quanto costa scaldare l’edificio per 6 mesi?

RISOLUZIONE:

Superficie totale dell’edificio: di cui 592m² di muri e 8m² di finestre.

dove q* è la densità di flusso termico (densità perché riferito all’unità di superficie).

. Il coefficiente del muro è e quello delle finestre con telaio in alluminio più vetrocamera 4÷12÷6 è . I valori 4÷12÷6 indicano lo spessore in mm degli strati che compongono la finestra. I numeri 4 e 6 si riferiscono agli strati di alluminio e indicano rispettivamente lo strato interno ed esterno. Ogni strato ha uno spessore diverso per diminuire la dispersione termica e impedire l’inquinamento acustico dall’esterno all’interno.

Per calcolare quanto costa scaldare l’edificio per 6 mesi occorre convertire questo tempo in secondi: .

.

2- Problema di transitorio tecnico:

Quanto tempo è necessario per portare da una temperatura di 0°C a una temperatura di 20°C l’edificio dell’esercizio precedente?

RISOLUZIONE:

, . Poiché questa è la potenza dispersa dall’edificio è necessario che la potenza fornita sia uguale a quella dispersa: la potenza aumenta linearmente con la temperatura. La temperatura però non dipende linearmente dal tempo, come si può vedere dal grafico seguente, ma raggiunge un valore limite (asintoto orizzontale), che dipende dalla potenza che sono in grado di fornire. Se quindi fornisco più potenza di quanto è necessario, la temperatura voluta sarà raggiunta in un tempo molto inferiore.

La conclusione è quindi che è conveniente fornire una potenza . Per ipotesi . Per avere una soluzione semplificata del problema ipotizziamo che il calore non venga disperso dalla casa durante la fase di riscaldamento. È chiaro che con questa ipotesi il tempo di riscaldamento sarà minore del tempo effettivo.

La massa del sistema è la massa d’aria, quindi .

L’energia necessaria per scaldare 1kg di acqua di 1°C è allora dove c_acqua indica la capacità termica specifica dell’acqua. La capacità termica specifica dell’aria è invece , la capacità termica dell’aria a pressione costante (cioè quando è libera di espandersi) è. Poiché in questo caso il volume è costante bisogna usare c_aria:

di riscaldamento quindi cioè circa 34 minuti.

Quanto costa scaldare quest’aria? Per prima cosa si trasformano i J in kWh, perché i contatori di casa calcolano il costo in base a questi ultimi:

e, poiché 1kWh costa 200£, scaldare questo volume d’aria costa 1024.2£.

Se invece l’aria fosse libera di espandersi, quindi la pressione è costante e il volume no:

. In kWh questo valore è:

quindi il costo in questo caso sarebbe 1436.6£

Il tempo di riscaldamento t è minuti.

Nel primo esercizio il valore T₂ (la temperatura esterna) è stato considerato nullo. Questo valore è importante per il calcolo della dispersione termica di un edificio e di conseguenza anche per il bilancio energetico dell’edificio stesso. Nella legge 10 del 9 gennaio 1991 vengono definite delle norme per il contenimento dei consumi di energia per quanto riguarda la progettazione, installazione, esercizio e manutenzione degli impianti termici. Inoltre questa legge considera anche altri aspetti quali la determinazione delle zone climatiche, la durata giornaliera di attivazione, i periodi di accensione degli impianti termici e la temperatura massima dell’aria negli ambienti degli edifici durante il funzionamento degli impianti.

Il 26 agosto 1993 fu pubblicato il D.P.R. (decreto del Presidente della Repubblica) 412, nel quale viene dato un valore limite del FEN cioè del fabbisogno energetico normalizzato per la climatizzazione invernale. Per “fabbisogno per riscaldamento” si indica la potenza termica dell’impianto di riscaldamento in conformità con la norma UNI 7357. Tale potenza è giustamente cautelativa (circa il doppio della potenza media richiesta nel mese di gennaio), perché l’impianto deve assolvere al suo compito anche in presenza di condizioni eccezionali, deve consentire l’intermittenza di funzionamento e deve sopperire alle variazioni di regime termico in tempi accettabili. Il fabbisogno di potenza secondo la norma UNI 7357 indica quale potenza dovrà avere l’impianto perché l’edificio possa essere riscaldato in qualsiasi condizione climatica e nelle previste condizioni di intermittenza.

La novità introdotta dalla legge 10/91 è invece il calcolo del fabbisogno annuo convenzionale di energia primaria (in MJ), che rappresenta il consumo totale, di combustibile e energia elettrica, entrambe tradotte in consumo combustibile (energia primaria) nella centrale termica dell’ENEL. Il suo scopo è ben diverso da quello del fabbisogno di potenza. Il dato di fabbisogno di energia, che rappresenta il consumo di riferimento, consente di conoscere a priori già in fase di progetto, quale sarà il consumo di combustibile del sistema edificio-impianto. Nella progettazione dei nuovi edifici consente di valutare le prestazioni di soluzioni diverse (edili ed impiantistiche) al fine di ottimizzare le scelte. Negli edifici già esistenti consente invece di valutare a priori e con notevole precisione gli effetti di possibili interventi di risparmio energetico e la loro convenienza economica. Il D.P.R. fa riferimento per il calcolo del fabbisogno energetico alla normativa UNI (da 10344 a 10349).

Il problema che si presenta è che vengono forniti tre diversi metodi di calcolo abbastanza lunghi e complessi che conducono ad un calcolo del fabbisogno energetico normalizzato FEN molto sovradimensionato. Questo numero, che non rappresenta affatto il fabbisogno di energia del sistema edificio-impianto, deve essere calcolato per legge per essere confrontato con il FEN limite, che similmente non ha significato pratico.

Si tratta infatti del prodotto fra una potenza cautelativa calcolata secondo UNI 7357 per il tempo: questo prodotto dà come risultato una “energia sbagliata”. La cosa non meriterebbe tanta attenzione se il calcolo imposto non fosse così preciso e laborioso da permettere il calcolo corretto dell’energia.

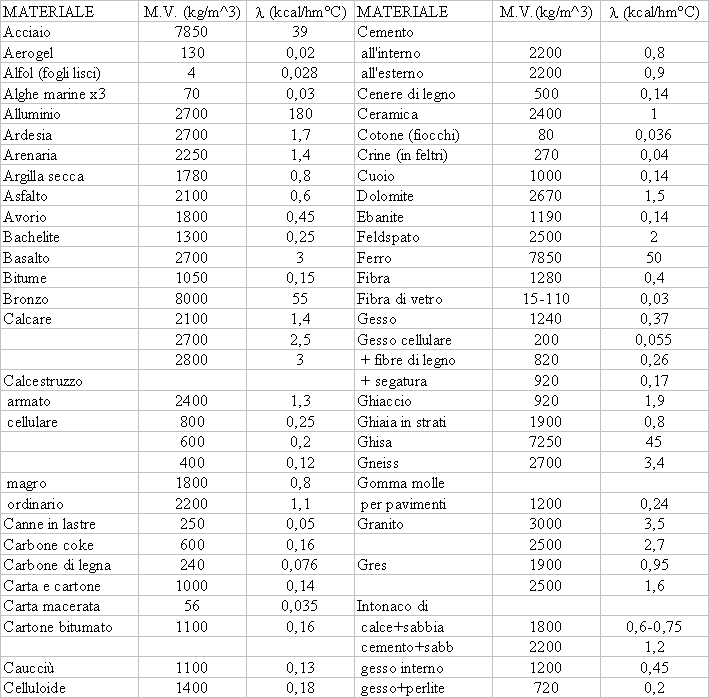
Nel primo esercizio è necessario l’uso dei valori k, cioè il coefficiente di conducibilità termica. I valori di k per ogni materiale da costruzione è indicato nella norma UNI 7357 nominata poco prima. Il problema è che per ogni materiale non viene fornito il valore k in m²K/W, ma viene fornita la conduttività l.

Questo rappresenta il flusso di calore che nelle condizioni di regime stazionario passa attraverso una parte di materiale omogeneo dello spessore di 1m, per m² di superficie e per una differenza di 1°C tra le due facce opposte e parallele della parete di materiale considerato. Le sue unità di misura sono dunque , mentre nel SI sono. Poiché , e , il fattore di conversione quindi è 0.00116306 circa.

Nelle tabelle della norma UNI 7357 viene inoltre fornito il valore della massa volumica del materiale in kg/m³.

I valori di k (W/m²K) per i diversi tipi di muro possono essere trovati nella norma UNI 10355. In essa è possibile trovare i diversi tipi di muro (una, due o tre teste) con mattoni di dimensioni differenti.

Nella tabella sottostante alla voce dimensioni si intendono quelle del singolo mattone, con lunghezza x altezza x profondità espresse in millimetri.

Vista la diversità di mattoni esistenti, nel primo esercizio ho lasciato il valore di k=0.5 W/m²K per evitare di complicare il calcolo. L’esercizio 1 è quindi solo un esempio di come vanno svolti i calcoli.