Micaela
Perazzo 139175
Lezione del 22\11\2001 ore 16:30-18:30
Gas perfetti
Sono gas elementari, molto semplici, a bassissima densità e in cui gli atomi che li compongono non interagiscono l'uno con l'altro. Una loro caratteristica fondamentale è che seguono rigorosamente le leggi di Boyle e di Gay-Lussac.
Legge di Boyle:
pv=k
Ovvero a temperatura costante, pressione e volume del gas sono inversamente proporzionali.
Prima legge di Gay-Lussac:
Vt=Vo (1+at)
Ovvero la variazione di volume di un gas, prodotta da una variazione di temperatura, a pressione costante, è direttamente proporzionale al volume a 0° C e alla variazione di temperatura, ma è indipendente dalla natura del gas.
Seconda legge di Gay-Lussac:
Pt=Po (1+at)
Ovvero la variazione di pressione di un gas, prodotta da una variazione di temperatura, a volume costante, è direttamente proporzionale alla pressione a 0° C e alla variazione di temperatura, ma è indipendente dalla natura del gas.
Equazione dei gas perfetti per una sola grammo-molecola di gas:
pv=RT
Equazione dei gas perfetti per un numero n di grammo-molecole di gas:
pv=nRT
Sapendo che:"u" è l'energia interna e "h" è l'entalpia, avremo:
![]()
e
![]()
Sapendo ancora che:
![]()
e
![]()
Lezione del 22\11\2001 ore 16:30-18:30
Esercizio n°1
In tutti e due i contenitori abbiamo inserito dell'aria,
che in questo caso consideriamo come un gas ideale, ma che in realtà è una miscela
di azoto e di ossigeno.
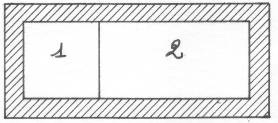
Sapendo che:
![]()
![]()
![]()
![]()
![]()
![]()
Trovare il valore di ![]() e di
e di ![]()
Per risolvere l'esercizio applichiamo il primo principio della termodinamica:
![]()
Ma
![]()
Avremo che:
![]()
Sapendo anche che:
![]()
e
![]()
Posso trovare M dall'equazione di stato dei gas perfetti,sapendo che:
![]()
Quindi abbiamo anche:
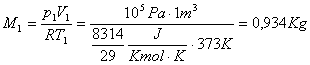
e
Lezione del 22\11\2001 ore 16:30-18:30
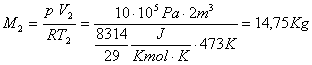
Da qui otteniamo:
![]()
Ma è vero anche che:
![]()
Quindi:
![]()
Ovvero:
![]()
Da qui otteniamo:
![]()
![]()
Per trovare
![]() uso la formula:
uso la formula:
![]()
Quindi:
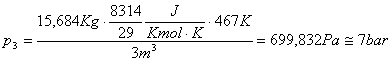
In questo esercizio si conservano sia la massa che l'energia.
Esercizio n°2
Abbiamo due contenitori in cui abbiamo inserito rispettivamente ossigeno e azoto, sapendo che:

![]()
![]()
Lezione del 22\11\2001 ore
16:30-18:30
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Trovare il
valore di ![]() e di
e di ![]() .
.
Sappiamo che:


Da qui abbiamo che:
![]()
Sappiamo ancora che:

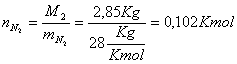
Da qui abbiamo che:
![]()
Ora troviamo la concentrazione rispettivamente di ossigeno e di azoto:
![]()
![]()
Dalla relazione:
![]()
Possiamo
trovare sia ![]() che
che ![]() , infatti:
, infatti:

Lezione del 22\11\2001 ore
16:30-18:30
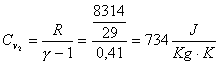
Per avere ![]() , si ricorre alla definizione dei calori specifici:
, si ricorre alla definizione dei calori specifici:
![]()

A questo
punto possiamo trovare anche ![]() :
:
![]()
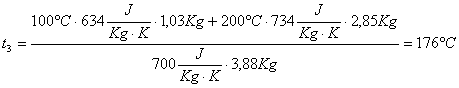
![]()
Ora
troviamo anche ![]() :
:
![]()
Ma:


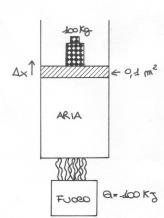
Esercizio n°3
Anche in quest'ultimo esercizio abbiamo inserito dell'aria in un contenitore sottoposto però al calore di un fornello sottostante ad esso.
Lezione del 22\11\2001 ore 16:30-18:30
Sapendo che:
![]()
![]()
![]()
![]()
Trovare
l'aumento di volume ![]() dell'aria e quindi
dell'aria e quindi ![]() .
.
Questo esercizio si può svolgere in due modi diversi:
Vediamo il METODO TRADIZIONALE:
partiamo dall'equazione di stato dei gas perfetti e troviamo il volume:
![]()
![]()
Quindi:

Ma:
![]()
Quindi:
![]()
Allora avremo che:
![]()
Vediamo ora il METODO ENERGETICO:
![]()
Ma:
![]()
![]()
![]()
Quindi:
![]()
Questo ci mostra che in qualunque modo decidiamo di risolvere il problema, arriviamo allo stesso risultato.