Le perdite di carico

Perdite di carico distribuite.

Prenderemo qui in esame il metodo utilizzato per calcolare una nuova grandezza R,detta perdita di carico;ossia l’energia dissipata per unità di tempo e di portata che risulta essere pari alla differenza di pressione diviso la densità del fluido.

(1)

Per praticità tali perdite vengono classificate in perdite di carico distribuite (Rdis) e concentrate (Rconc).

Per capire meglio prenderemo ad esempio un tubo cilindrico,retto e uniforme nel quale scorre un fluido.

Consideriamo ora la sezione 1-2 ove non sono presenti impedimenti (quali rubinetti e valvole) e per la quale varrà ancora l’equazione (1).

Se la dissipazione dell’energia dipende dal numero di Reynolds,dalla lunghezza del tubo e non dalla variazione delle sezioni attraverso cui passa il fluido,è indicata con il nome di perdita di carico distribuita.

Per capire al meglio la logica di base,è necessario fare un piccolo passo indietro nel mondo della fisica e introdurre il principio di similitudine in quanto per questi complicati casi,non sono state delineate né una teoria,né dei calcoli chiari e semplici.Bisogna allora procedere per esperimenti che di volta in volta daranno valori diversi tra loro di R.Da tali esperimenti risulta inoltre che R dipende dalle seguenti grandezze:scabrezza,diametro del tubo e numero di Reynolds. Risulta chiaro che se le tre grandezze sono uguali,non si necessita di molti esperimenti in quanto il risultato sarà sempre lo stesso,indipendentemente dal fluido preso in esame.

R= f (eDRe)

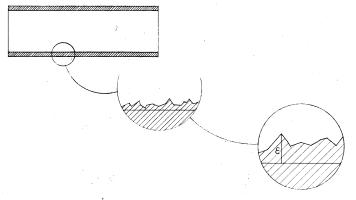
Apriamo un attimo una parentesi e definiamo la scabrezza e.

Se prendiamo un tubo,ne ingrandiamo una parte ci accorgeremo che spesso le superfici dei condotti nei quali scorrono i fluidi,non sono lisce ma mostrano delle irregolarità dovute alla natura del materiale e ai procedimenti di realizzazione dei condotti stessi.La scabrezza risulta essere l’altezza tra gola e punta ossia quanto è discontinua la superficie.

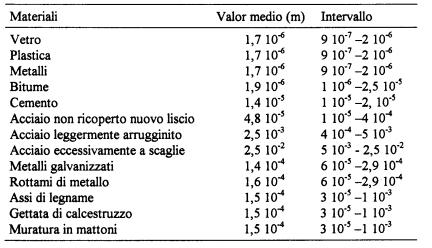
Nella seguente tabella sono mostrati i valori medi e gli intervalli di variabilità della scabrezza.

Ritornando alle perdite di carico distribuite,l’equazione per calcolarle risulta essere:

2

R= l L W

D 2

l =coefficiente di attrito da calcolarsi caso per caso in quanto varia a seconda della sezione del

condotto (a sezione circolare) e della sua scabrezza.Si calcola cosi: 64

L Re

D =lunghezza/diametro tubo

2

W

2 =energia cinetica

Per un condotto a sezione circolare, il coefficiente di attrito per moto stabilizzato in funzione del numero di Reynolds e del parametro scabrezza, è rappresentato nel diagramma di Moody:

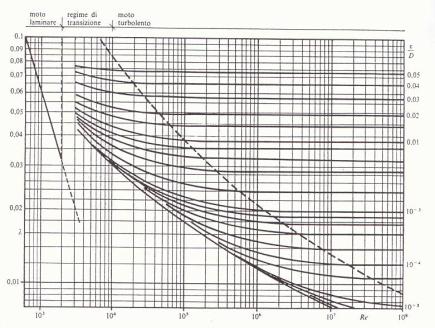
In questo diagramma sono riportati in ascissa il numero di Reynolds e in ordinata il fattore di attrito,entrambi in scala logaritmica.

Si noti che questo abaco è suddiviso in tre zone:

-nella prima il moto del fluido avviene per filetti paralleli (laminare) per cui la scabrezza del tubo non incide.Avremo allora numeri di Reynolds fino a 2300 e la curva sarà una retta.(caso poco comune,valido per oli combustibili con viscosità alta e bassa velocità)

-la seconda risulta essere una zona di transizione per la quale non si conosce l’andamento del diagramma.(ristretta e difficile da prevedere)

-la terza,la più comune,è definita dal regime turbolento e inizia per Re=4100. Qui la scabrezza del tubo incide molto:più è scabro,più saranno le perdite.Solitamente si preferisce essere in questa zona in quanto si crea una situazione di scambio termico,ovvero in presenza di moto turbolento c’è un maggiore mescolamento che facilita il nascere di calore.

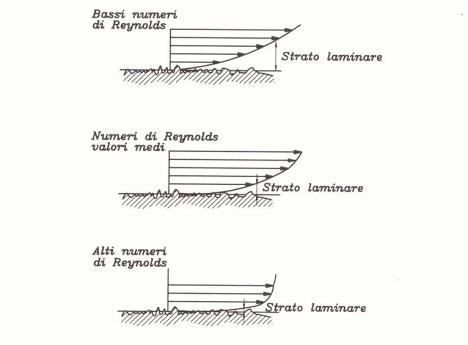
In questa ultima zona troveremo allora delle curve,curve che avranno un andamento discendente,tenderanno a spianarsi fino ad arrivare ad un andamento orizzontale.

Se in un problema vengono dati il fattore di scrabrezza del tubo e Re grazie al diagramma di Moody si può facilmente ricavare il valore del fattore d’attrito;basta tracciare una riga verticale che parte dal valore di Re e arriva alla curva che rappresenta la rugosità relativa del condotto e quindi dal quel punto tracciare una riga orizzontale fino al valore del fattore di attrito desiderato.Se il numero di Reynolds è un’incognita del problema si deve procedere alla risoluzione per tentativi.

Nel caso in cui non abbiamo un tubo cilindrico,ma di altre forme, sempre regolari,posso utilizzare le stesse formule e lo stesso diagramma introducendo però il concetto di diametro equivalente dato dal rapportotra quattro volte l’area della sezione e il perimetro bagnato (parte del tubo dove c’è contatto tra fluido e pareti)

Alcuni esempi:

=L

De = 4 A

2 Pbagnato dato dalla somma dei tre lati bagnati

Potremmo cosi calcolare tutti i casi che si presenteranno a noi.

Perdite di carico concentrate

Nel caso in cui, la causa fondamentale di dissipazione è data dalla configurazione geometrica o dalla presenza di eventuali accidentalità,come curve,gomiti,valvole,rubinetti,avremo perdite di carico dette concentrate.Questa denominazione dipende dal fatto che esse sono localizzate in punti precisi del condotto e non distribuite per tutta la lunghezza del tubo.

Per calcolare tali perdite si utilizza la seguente espressione:

Indicando con b un coefficiente in funzione solo della geometria,w è la velocità media di scorrimento del fluido.

I valori di b, per i casi più comuni, sono riportati in una tabella che affianca a ogni valore del fattore di attrito il suo caso specifico di perdita di carico.

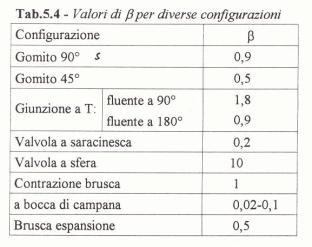
In definitiva risulta che per calcolare le perdite di carico R,dovrò sommare le perdite distribuite a quelle concentrate:

R= Rdis + Rconc

Lunghezza equivalente

Nel caso in cui però,lungo un condotto si verificano sia perdite di carico concentrate che distribuite,per calcolare le perdite di carico totale,si può utilizzare il metodo delle lunghezze equivalente.E’ possibile in pratica assimilare ad ogni perdita di carico concentrata che si verifica in un punto del condotto,una perdita distribuita in un condotto dello stesso diametro e con un certo valore di lunghezza,detta appunto lunghezza equivalente.La relazione che esprime le perdite concentrate, si converte nella relazione usata per le perdite distribuite, con la sola sostituzione della lunghezza equivalente al termine L:

Per calcolare la lunghezza equivalente,si utilizza la seguente tabella:

In questa tabella troviamo tre assi verticali e tra loro paralleli,nei quali possiamo leggere su quello di destra i valori del diametro interno della sezione del tubo riportati in millimetri,su quello centrale la lunghezza equivalente espressa in metri e su quello di sinistra i valori corrispondenti alle accidentalità del tubo.Per ricavare quindi il valore della lunghezza equivalente,basterà conoscere il diametro interno del tubo,il tipo di accidentalità e mi verrà indicato dal valore del punto di intersezione tra la retta tracciata per congiungere i punti che mi indicano i valori noti,con l’asse centrale.

Esercizi svolti:

1)Abbiamo un serbatoio alla quota nota di 2 metri dal quale usce un tubo e del quale vogliamo calcolare la portata d’acqua in uscita.Sono note tutte le curve caratteristiche.

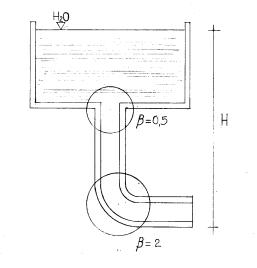
Dati:

H= 2 m

D= 2 cm

L = 4 m

b = 20 mm

Iniziamo applicando il teorema di Bernulli:

Da notare che:

l = 0 in quanto non sono presenti né pompe né turbine

.

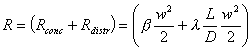
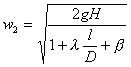. risulta essere l’incognita ma l non è fisso e varia con Re; allora conoscendo e procederò per iterazione ossia farò vari tentativi proponendo diversi valori di l (per comodità conviene partire da un caso di turbolenza,per avere una corrispondenza diretta tra e l) finchè non ne otterrò uno accettabile in cui avrò .

e

D =0,001 da qui trovo un l di primo tentativo,pari a 0,023 e lo ricavo sul diagramma di Moody guardando qual è il valore minimo di e e a quale l corrisponde.Utilizzerò inoltre una tabella come la sottostante:

D

N° tentativo		Re	l
1			0.023	2.20 m/s
2	2.20	44000	0.0247	2.156 m/s
3	2.156	43000	0.025	2.15 m/s

Al terzo tentativo abbiamo trovato la velocità dell’acqua che è di 2,15 m/s ora quindi possiamo calcolare la portata:

In questo caso ci troviamo nella zona turbolenta.

2)Abbiamo due serbatoi la cui altezza (H) tra i peli liberi è 50 metri;si deve determinare la potenza della pompa che dovrò sistemare per portare dal serbatoio 1 al serbatoio 2 una portata pari a 20 l/s.

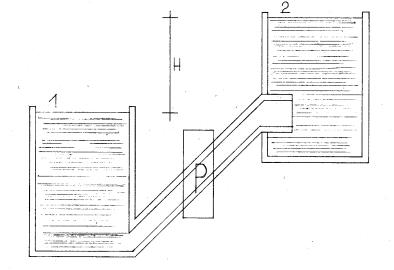
Dati:

H= 50 m

D= 100 mm

L= 1 km

Iniziamo applicando Bernulli sotto questa formula:

Calcoliamo la velocità in uscita da inserire poi nell1equazione sopra:

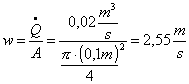
Troviamo il numero di Reynolds per vedere che tipo di moto si genera all’interno del condotto:

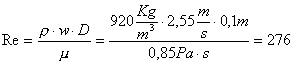
In questo caso trascuro le perdite concentrate in quanto a causa della lunghezza di 1 km le perdite di imbocco e uscita non incidono.Calcolando l = 64/Re = 0,23 notiamo che ci troviamo in un regime laminare e quindi avrò che le perdite saranno:

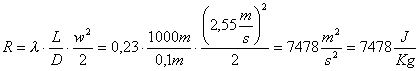
_{Dalla precedente relazione di Bernulli potrò calcolare il lavoro specifico della pompa:}

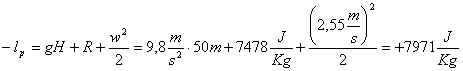
_{e per calcolare la potenza che dovrà avere:}