Gualdi Derna - matr. 141092 - Lezione del 25/10/2001 - ora 16:30-18:30

Trasformazioni dei gas

Lo stato di un sistema termodinamico in equilibrio con l’ambiente è caratterizzato da grandezze, o variabili, di stato, che sono: PRESSIONE, VOLUME e TEMPERATURA. Esse sono collegate tra loro e il nostro scopo è quello di individuare le leggi fisiche che esistono tra di esse quando un gas passa da uno stato di equilibrio iniziale ad uno finale, cioè quando il sistema subisce una TRASFORMAZIONE.

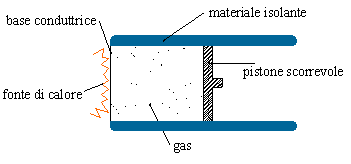
Per fare ciò, supponiamo di avere una certa quantità di gas racchiuso in un cilindro (fatto di materiale isolante) dotato di un pistone scorrevole (con attrito trascurabile) sulle pareti del recipiente.

Notiamo quindi quattro diversi tipi di trasformazione del gas:

• ISOBARA: si mantiene fissa la pressione e vengono fatte variare la temperatura (ad esempio scaldando la base conduttrice) e il volume (muovendo il pistone), i quali risultano essere direttamente proporzionali tra loro. L’equazione che lega le due variabili è data dalla prima legge di Gay-Lussac:

(1)

dove V_f rappresenta il volume finale, dopo la trasformazione, V_i il volume iniziale ad una temperatura di 0° C, a una costante pari a 1/273° C e T_f la temperatura finale espressa in gradi kelvin.

• ISOCORA: si mantiene costante il volume del gas e vengono variate temperatura e pressione. Anche in questo caso le due variabili sono legate da un rapporto di proporzionalità, definito dalla seconda legge di Gay-Lussac (detta anche legge di Charles):

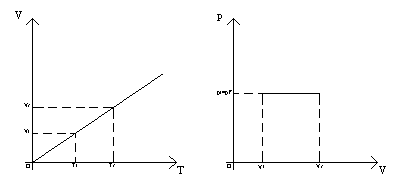
(2)

dove p_f è la pressione finale, p_i è la pressione iniziale ad una temperatura di 0° C, a è una costante pari a 1/273° C e T_f la temperatura finale espressa in gradi kelvin.

• ISOTERMA: si mantiene costante la temperatura e si fanno variare pressione e volume, legati da un’indiretta proporzionalità e quindi dall’equazione:

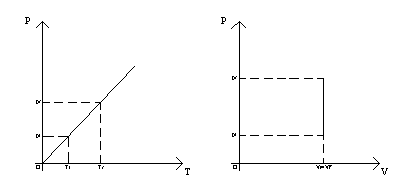
(3)

Questa legge prende il nome da Robert Boyle , il primo a determinarla sperimentalmente, nel 1662.

• ADIABATICA: nel considerare questa quarta trasformazione bisogna premettere che la base del cilindro viene qui ricoperta da uno strato isolante. Per questo motivo vi è una totale indipendenza termica dall’esterno, cioè il gas all’interno del cilindro non scambia calore con l’esterno, quindi Q = 0. La legge che lega la pressione al volume è:

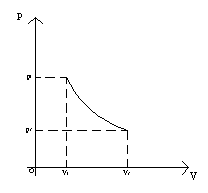
(4)

dove g = c_p/c_V rappresenta il rapporto tra il calore specifico a pressione costante c_p e il calore specifico a volume costante c_V.

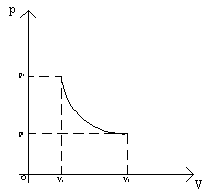
Il confronto con il ramo di iperbole di una trasformazione isoterma a 0° C, evidenza la maggiore ripidità della curva relativa alla adiabatica.

Un quadro d’insieme delle trasformazioni è il seguente:

dove + indica che la variabile di stato aumenta, - diminuisce, k rimane costante

Equazione di stato dei gas

Ci poniamo ora il problema di determinare una legge più generale che leghi le variabili di stato per qualsiasi trasformazione del gas; ovviamente questa legge dovrà contenere quelle precedentemente illustrate. Si può dimostrare che questa legge generale, detta EQUAZIONE DI STATO, per i gas perfetti ha la seguente forma:

(5)

dove n indica il numero di moli di gas, R la costante dei gas perfetti pari a 8,314 J/molK e p, V, T le variabili di stato dei gas (rispettivamente pressione, volume, temperatura). Un altro modo di esprimerla, mettendo in evidenza la massa del gas m (espressa in kg) invece del numero di moli, può essere:

(6)

dove questa volta R vale c_p-c_V.

Tralasciando la dimostrazione rigorosa del procedimento con cui si ricava la legge dei gas perfetti dalla legge di Boyle e dalle due leggi di Gay-Lussac, si può facilmente verificare che queste ultime sono contenute, come caso particolare, nell’equazione dei gas perfetti. Infatti se T = costante, il prodotto mRT è anch’esso costante e quindi si ha pV = costante. Se p = costante, si ha V= (mR/p)T e quindi V= costante*T; in modo analogo si può verificare anche la seconda legge di Gay-Lussac.

E’ utile osservare come l’equazione di stato dei gas perfetti, e quindi il comportamento del gas, sia influenzato dal numero di molecole e non dalla massa.

Attenzione: se il gas non è in contatto termico con l’ambiente (trasformazione adiabatica) all’equazione di stato dei gas si aggiunge l’equazione (4).

Bilancio dell’energia (Q-L)

Consideriamo ora il bilancio Q-L in tre possibili trasformazioni sul grafico pV per un gas perfetto che sia inizialmente ad una temperatura T_i (data) e nello stato V_ip_i, e alla fine nello stato V_fp_f.

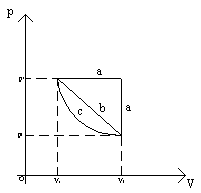
Dalle condizioni generali possiamo supporre che il cammino più conveniente, cioè quello che necessita di meno lavoro sia il c, visto che l’incognita Q risulta essere nulla, essendo una trasformazione adiabatica. Avremo quindi il sistema:

(7)

dove g vale c_p/c_V ed m e T_f sono le incognite da calcolare. Dalla prima equazione ricavo che m = p_iV_i/RT_i; sostituisco poi questo risultato nella seconda equazione e determino T_f = p_fV_f/mR. La terza equazione del sistema risulta essere sottintesa, dal momento che il punto iniziale e il punto finale vengono definiti. Di conseguenza sono in grado di calcolare il lavoro compiuto: dal primo principio della termodinamica so che U_f-U_i = Q-L, ed in particolare so che per i gas perfetti l’energia interna U = mc_VT. Quindi posso unire le due equazioni nella forma:

(8)

dove L_c è il lavoro compiuto dal gas nel caso c.

Per l’analisi degli altri due percorsi è utile specificare che il lavoro compiuto vale ; è perciò rappresentato dall’area sottesa al grafico di p in funzione di V.

Il lavoro compiuto durante il percorso a dipende dall’area del rettangolo che ha per basi D V = V_f-V_i e p_f. Risulta quindi:

(9)

dove L_a rappresenta il lavoro compiuto nel percorso a. Possiamo ora determinare con il primo principio della termodinamica:

(10)

dove Q_a rappresenta il calore fornito lungo la trasformazione a ed è facile da calcolare visto che la variazione (U_f-U_i) è la medesima per ogni percorso, in quanto tutti e tre partono dallo stesso punto (stessa condizione iniziale) V_ip_i e arrivano allo stesso punto finale (stessa condizione finale) V_fp_f. Si può quindi notare come il primo principio della termodinamica non dipenda dal cammino percorso, ma solo dai punti di partenza e di arrivo. Quindi nel caso in cui il punto finale coincida con quello iniziale, cioè nel caso di un ciclo, la variazione di energia interna risulta essere nulla.

Il percorso b, invece, sottende un’area trapezoidale, alla quale corrisponde un lavoro L_b pari a:

(11)

come prima possiamo determinare la quantità di calore fornita durante il cammino b:

(12)

ATTENZIONE: il lavoro calcolato, in ognuno dei tre percorsi, è stato compiuto veramente tutto? La risposta è no, perché ci ha aiutato la pressione atmosferica pari ad 1 bar.

Quindi è meglio dire:

(13)

dove p₀ è la pressione atmosferica. Di conseguenza risulta che il lavoro totale, L_tot, è:

(14)

mentre il lavoro netto, L_netto, è:

(15)

Esercizio

Ripetiamo queste considerazioni nel caso in cui il cilindro contenga aria. Ed in particolare che:

la temperatura iniziale: T_i = 600K,

la pressione iniziale: p_i= 32 bar =3200000 Pa

la pressione finale: p_f= 1 bar =100000 Pa

il volume iniziale: V_i= 1 m³

il volume finale: V_f= 8 m³.

Calcoliamo ora la quantità di calore Q fornita e il lavoro L compiuto per ogni singola trasformazione:

• trasformazione c: impostiamo il sistema

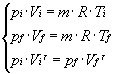
dal quale ricaviamo che

sostituiamo poi il valore ottenuto nella seconda equazione del sistema per trovare la temperatura finale

Ora siamo in grado di determinare il lavoro compiuto lungo il percorso c: dall’equazione del primo principio della termodinamica sappiamo che

ma in questo percorso (curva adiabatica), non essendoci scambio termico con l’esterno, il lavoro Q è nullo, quindi

Noi sappiamo però che

Possiamo quindi eguagliare le ultime due equazioni viste e ottenere il lavoro speso per il percorso c

(ricordandosi di cambiare il segno perché il lavoro esce).

• trasformazione b: per calcolare il lavoro compiuto lungo il percorso b, dobbiamo considerare l’area sottesa alla retta che unisce il punto iniziale p_iV_i e il punto finale p_fV_f. per cui dobbiamo calcolare l’area del trapezio che ha per base minore p_f, per base maggiore p_i e per altezza (V_f-V_i)

Essendo il punto iniziale e il punto finale coincidenti la variazione di energia interna (U_f-U_i) è la stessa per ogni percorso, quindi posso riutilizzare il valore ottenuto precedentemente e calcolare

• trasformazione a: ora devo invece calcolare l’area del rettangolo che ha per base (V_f-V_i) e per altezza p_f

Facendo lo stesso ragionamento di prima avremo poi che