Matteo Gargallo 138748 lezione del 15-11-2001 ore:14.30-16.30
CAMBIAMENTI DI STATO DI
AGGREGAZIONE IN SISTEMI CHIMICAMENTE OMOGENEI
GLI STATI DI AGGREGAZIONE
DELLA MATERIA
La materia che ci circonda è composta da aggregati di particelle (atomi o molecole). A
seconda della distanza tra le particelle e della libertà di movimento che esse
godono le une rispetto alle altre, la materia
si presenta in tre diversi stati di aggregazione: lo stato solido,
lo stato liquido
e lo stato aeriforme.
In determinate condizioni di temperatura e pressione la materia può cambiare
stato di aggregazione, assumendo
diverse caratteristiche chimico- fisiche. Tutti i possibili cambiamenti di
stato sono riportati nello schema seguente (fig.1):
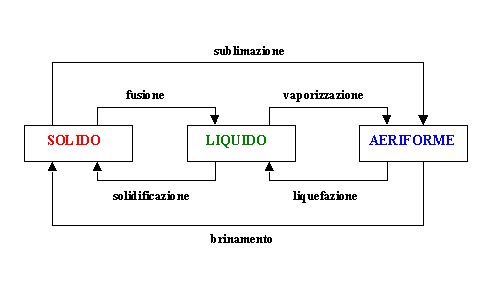
fig.1 - Passaggi di stato
Fornendo calore ad una sostanza si accresce
l’energia cinetica delle sue particelle, le quali possono così vincere le forze
di coesione e passare, nella maggior parte dei casi, a stati di aggregazione a
minore densità (solido→liquido→aeriforme). Sottraendo invece calore,
si sottrae energia cinetica alle particelle, favorendo così il passaggio a
stati di aggregazione a maggiore densità (aeriforme→liquido→solido).
Il modo più semplice per studiare dal punto di vista
termodinamico i cambiamenti di stato di aggregazione è quello di considerare un
sistema chiuso chimicamente omogeneo.
Ma cos’è un sistema chiuso chimicamente omogeneo?
E’ innanzitutto un sistema chiuso, cioè un sistema che scambia con l’ambiente esterno solo calore e lavoro, mantenendo la propria massa costante, ma è anche un sistema in cui sono presenti sostanze chimicamente pure, quali per esempio l’acqua, l’alcool, l’azoto o l’ossigeno. Un sistema chimicamente omogeneo può essere a una sola fase (o solida, o liquida, o aeriforme ) o a più fasi (solida-liquida, liquida-aeriforme, solida-aeriforme), il tutto al variare di 3 grandezze termodinamiche:
p Þ pressione assoluta [Pa]
v Þ volume specifico
ovvero VTOT / MTOT [ m3/kg]
T Þ temperatura assoluta [K]
Conoscendo i valori di queste tre grandezze è
possibile definire lo stato termodinamico del sistema, ma è anche possibile
ricavare da esse altre proprietà termodinamiche come l’energia interna,
l’entalpia e l’entropia che non sono direttamente misurabili.
DIAGRAMMI TERMODINAMICI
Considerato un sistema chimicamente omogeneo e chiuso è possibile riportare i suoi valori di pressione, temperatura e volume specifico in un sistema di assi cartesiani XYZ. Si ottiene così il diagramma termodinamico del sistema, che è rappresentato da una superficie di complessità variabile i cui punti rappresentano ciascuno un determinato stato termodinamico (fig. 2).
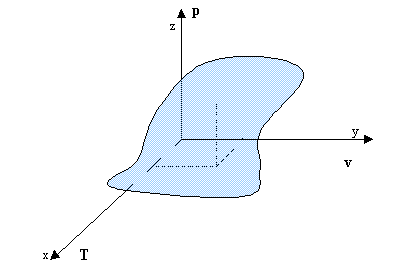
fig. 2 -
Diagramma p-T-v
In un sistema chimicamente omogeneo le grandezze p, T, v sono legate da una relazione chiamata
funzione di stato, che ne limita
l’indipendenza. Conoscendo il numero delle grandezze indipendenti e il loro
valore è possibile ricavare tramite questa relazione le grandezze dipendenti.
Il numero delle grandezze indipendenti (o gradi di libertà) in un sistema
termodinamico si ricava tramite la legge
di Gibbs.
LA LEGGE DI GIBBS
Se definiamo con
· P Þ n° delle grandezze indipendenti (che possono assumere un qualsiasi valore)
·
M Þ n° dei componenti chimici
del sistema
·
F Þ n° delle fasi presenti nel
sistema
abbiamo
che
P = M + 2 -
F (1)
Facciamo
alcuni esempi.
Esempio 1
Calcolare i gradi di libertà di un sistema chimicamente omogeneo e chiuso costituito da vapor d’acqua.
In questo caso:
M=1 perché il sistema è costituito da sola acqua
F=1 perché c’è una sola fase
Da ciò abbiamo che P = 1 + 2 - 1 = 2. Quindi il numero delle grandezze termodinamiche
indipendenti sono due e la terza dipenderà da queste due. Da ciò deriva che
nota sul diagramma termodinamico una coppia p-v o v-T o p-T è possibile ricavare la terza
grandezza.
Esempio 2
Calcolare i gradi di libertà di un sistema chimicamente omogeneo costituito da ghiaccio che si sta sciogliendo.
In questo caso:
M= 1
F= 2 perché
le fasi del sistema sono due
Da
ciò abbiamo che P = 1 + 2 - 2 = 1. Quindi conoscendo il
valore di una grandezza è possibile determinare le altre due.
In questi due esempi abbiamo considerato come sostanza costituente il sistema l’acqua in due stati di aggregazione diversi. Proprio per le sue buone caratteristiche termodinamiche, tra i diagrammi p-T-v di tutti i liquidi, quello dell’acqua si presta ad un’analisi più approfondita.
IL DIAGRAMMA p-T-v DELL’ACQUA
Come si osserva dalla figura (fig.3), la superficie del diagramma dell’acqua è molto complessa e per ricavarne informazioni utili si ricorre alla sua proiezione nella direzione degli assi su dei piani ausiliari.
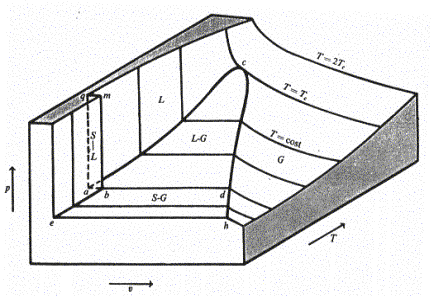
Fig.3- Diagramma termodinamico dell’acqua
PROIEZIONE SUL PIANO p-v
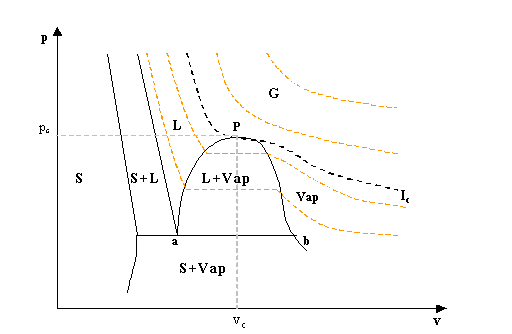
fig. 4- Diagramma p-v dell’acqua
Tutte le proiezioni del diagramma tridimensionale sui diversi piani non hanno una scala lineare, ma vengono appositamente deformate per capire meglio l’andamento delle varie curve. Osservando il diagramma p-v (fig.4) si possono individuare delle zone e delle curve molto importanti.
Le superfici contrassegnate con S, L, G e Vap rappresentano le regioni del diagramma corrispondenti rispettivamente allo stato solido, liquido e aeriforme dell’acqua. Vi sono poi regioni in cui lo stato è definito dalla coesistenza di due fasi in equilibrio; di tali regioni ne esistono tre: solido-liquido (S+L), solido-vapore (S+Vap), liquido-vapore (L+Vap). Infine la linea congiungente i punti a-b costituisce la linea di intersezione di due regioni bifase ed è quindi una linea trifase, lungo la quale le fasi solida, liquida e aeriforme coesistono in equilibrio.
Le isoterme
Per determinare i valori della temperatura vengono introdotte sul diagramma delle curve chiamate isoterme (fig.4), sulle quali la temperatura è costante. In particolare l’isoterma Ic è chiamata isoterma critica, sulla quale la temperatura vale 647 K (ovvero 374 °C), detta temperatura critica (tc). Il punto P dell’isoterma critica prende il nome di punto critico, in cui lo stato dell’acqua è definito dai tre valori critici tc , vc (volume critico), pc (pressione critica) . Tutte le isoterme al di sotto della isoterma critica presentano un tratto orizzontale, che è tanto più lungo quanto più bassa è la temperatura. Unendo gli estremi di questi tratti orizzontali si ottiene una curva a forma di campana chiamata curva di Andrews.
L’isoterma critica e la curva di Andrews dividono il piano v-p in diverse regioni, a ciascuna delle quali corrisponde uno stato fisico diverso (fig.5 )
La parte A situata al di sopra dell’isoterma critica è la regione dei gas: nessuna pressione, per quanto elevata, può provocare la liquefazione dell’aeriforme (in questo caso dell’acqua) che si trovi in tale stato.
La parte B situata al di sotto della isoterma critica e alla destra della curva di Andrews è la regione dei vapori non saturi: la temperatura del vapore d’acqua può essere diminuita, entro certi limiti, senza che si verifichi la liquefazione.
La zona C al di sotto della curva di Andrews è la regione dei vapori saturi: ogni diminuzione di temperatura provoca la liquefazione.
La zona D sotto l’isoterma critica e alla sinistra della curva di Andrews è la regione del liquido.
Il tratto di curva d-P rappresenta lo stato di liquido saturo, mentre il tratto di curva P-e rappresenta lo stato di vapor saturo secco.
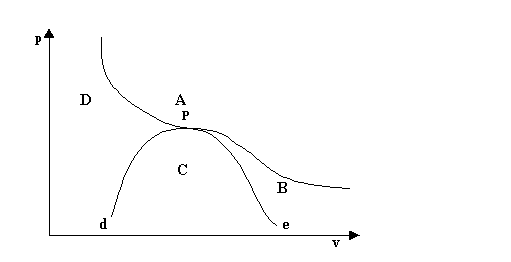
fig.5
DIAGRAMMA p-T
Proiettando il diagramma p-T-V sul piano p-T si ottiene il seguente diagramma bidimensionale (fig.6).
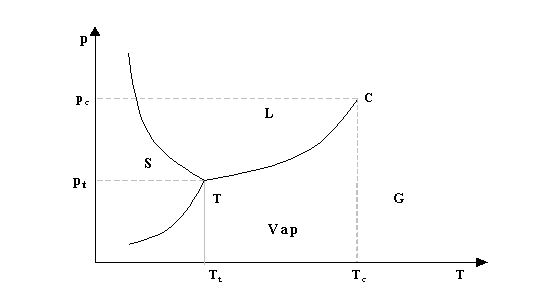
fig.6- Diagramma p-T dell’acqua
Le tre curve caratterizzanti questa proiezione rappresentano i passaggi tra i vari stati di aggregazione dell’acqua. Inoltre si incontrano in un punto chiamato punto triplo nel quale coesistono tutte e tre gli stati solido, liquido e aeriforme. Del punto triplo per convenzione si conosce la temperatura Tt = 0,01 °C (273,01 K) e la pressione Pt= 611 Pa. Volendo calcolare il numero delle grandezze indipendenti nel caso del punto triplo si ha che P= 1 + 2 - 3= 0.
Il punto C invece è il punto di temperatura critica, oltre il quale l’acqua ha un comportamento simile a quello dei gas ideali.
Il diagramma p-T permette inoltre di fare alcune considerazioni sull’influenza che ha la pressione sul punto di fusione dell’acqua, ovvero sul valore della temperatura in cui l’acqua passa dallo stato solido a quello liquido. In particolare si nota che l’aumento di pressione provoca un aumento del punto di fusione dell’acqua che a pressione ambiente è 0° C (273 K). Tale fenomeno spiega, per esempio, il lento scorrimento verso valle dei ghiacciai: il ghiaccio premendo contro le rocce si
scioglie. Un altro esempio di tale fenomeno è il seguente (fig.7).
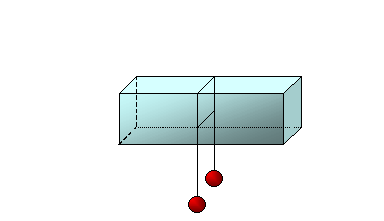
fig.7
Un filo a cui sono appesi due pesi viene posto su di un blocco di ghiaccio. Lentamente il filo, esercitando una forte pressione, provoca la fusione del ghiaccio e penetra in esso. Nei punti già attraversati dal filo, venendo meno la pressione ed essendo la temperatura inferiore a 0°C, si verifica il fenomeno del rigelo. In tal modo il filo attraversa il tutto il ghiaccio, senza però dividerlo.
Esempio 3
Nell’esempio seguente (fig.8) analizziamo in che modo avviene il passaggio di stati di aggregazione per un blocco di ghiaccio a cui una sorgente fornisce del calore uniformemente nel tempo, supponendo che il tutto avvenga a pressione ambiente costante e in un sistema chiuso.
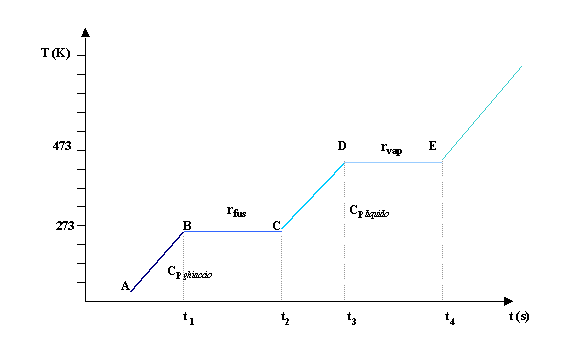
fig.8
Tratto A-B (stato
solido)
Dopo un certo tempo t1 la sorgente di calore ha riscaldato il corpo portandolo alla temperatura di fusione 273 K (circa 0°C). Lungo questo tratto ci è nota una grandezza che è il calore specifico del ghiaccio (Cp ghiaccio ), pari a 1900 J/kg K
che è la quantità di calore utile per scaldare 1 kg di ghiaccio di un grado.
Tratto B-C (stato
solido+liquido)
Arrivato alla temperatura di fusione il ghiaccio incomincia a sciogliersi percentualmente, ma per un certo tempo t2, pur continuando a fornire calore, la temperatura resterà invariata, e ciò fino a che il ghiaccio non si sarà sciolto completamente. Questa quantità di calore viene chiamata calore latente di fusione e per l’acqua vale 1600000 J/kg.
Tratto C-D ( stato
liquido)
Lungo questo tratto conosciamo un’altra grandezza che è il calore specifico del liquido ovvero la quantità di calore utile per riscaldare 1 kg di acqua di un grado ed è pari a 4187 J/kgK.
Tratto D-E (stato
liquido+vapore)
Anche il passaggio liquido- vapore avviene tramite l’uso di un calore latente chiamato calore latente di vaporizzazione (rv) pari per l’acqua a 2257000 J/kg.
Ad un certo punto tutta l’acqua si sarà trasformata in vapore e si avrà lo stato aeriforme. La temperatura dell’ acqua aumenta fino a raggiungere la temperatura critica dopo di che si comporta come un gas.
CONCETTO DI TITOLO
Tornando a considerare il diagramma p-v dell’acqua e in particolar modo la regione sottostante la campana di Andrews possiamo introdurre il concetto di titolo. Il titolo permette di individuare la percentuale di liquido e vapore nei diversi punti della regione considerata.
TitoloÞ x = m vap / (m l + m vap ) (2)
con m vap che indica la massa del vapore e m l che indica la massa della parte liquida. Il valore del titolo per come è definito varia tra 0 e 1 e in particolar modo vale 0 lungo il tratto della curva di Andrews che confina con la regione del liquido, mentre vale 1 lungo il tratto che confina con la regione del vapore. All’interno della campana si individuano inoltre delle altre curve chiamate ad isotitolo (fig.9), lungo le quali il titolo è costante.
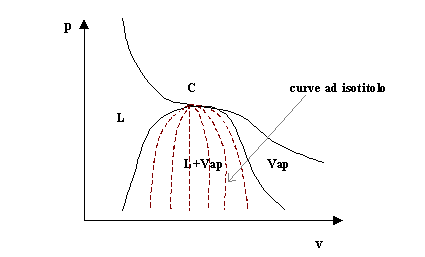
fig.9- Curve ad isotitolo nel diagramma p-v
In questa regione del diagramma, dove sono presenti due fasi cambia anche il concetto di volume specifico v che si calcola in questo modo:
(m l + m v ) v = m l v l + m v v v (3)
dove v l e vv sono i volumi specifici .
Utilizzando la definizione di titolo si ha che
v = (1-x) v l + v v (4)
e da questa si ha che
x = (v - v l ) / (v v - v l) (5)
dove v v - v l rappresenta il volume differenziale vd ovvero il variare del volume specifico durante il passaggio di stato.
A questo punto è possibile ricavare il volume medio in funzione del titolo
v(x) = v l +
x vd
(6)
Grazie al concetto di titolo è possibile ricavare il valore di altre grandezze importanti:
ENERGIA INTERNAÞ U(x) = Ul + x Ud (7)
ENTALPIAÞ h(x) = hl +
x hd
(8)
ENTROPIAÞ s(x) = sl + x sd (9)
Dove Ud = Uv-Ul ; mentre sd = sv -sl .