CORSO DI FISICA TECNICA A

ANNO 2001/2002

Prof. ANGELO FARINA

FACOLTA’ DI ARCHITETTURA – UNIVERSITA’ DEGLI STUDI DI PARMA

Sia dato un sistema chiuso che scambia con l’esterno, nell’intervallo di tempo dt, il lavoro elementare dL e il calore elementare dQ. La relazione che esprime il primo principio è precisata con l’introduzione di altri due termini energetici che caratterizzano il sistema nella sua costituzione e condizioni istantanee: il primo, definito in relazione ad un riferimento spazio-temporale, viene scisso in variazione dell’energia cinetica dE_c e variazione dell’energia potenziale dE_p. Il secondo, che può essere definito indipendentemente da ogni riferimento esterno, è detto variazione dell’energia interna dU. La relazione si scrive dQ=dE_c+dE_p+dU+dL. Se il sistema chiuso è fermo rispetto al riferimento inerziale, risulta dE_c=0, e se inoltre la dEp è dovuta tutta al campo gravitazionale, è anche dE_p=0; pertanto la precedente diventa dQ=dU+dL. La U è una funzione delle variabili necessarie per definire il sistema, è cioè funzione dello stato del sistema. Riassumendo la variazione di energia interna di un sistema è pari alla somma del lavoro svolto (positivo se fatto dal sistema, negativo se subito) e del calore scambiato dal sistema (positivo se assorbito, negativo se ceduto).

L’entalpia è una funzione di stato di un sistema ed esprime la quantità di energia che esso può scambiare con l’ambiente. In una reazione chimica, ad esempio, l’entalpia scambiata dal sistema consiste nel calore assorbito o rilasciato nel corso della reazione. Nel caso di un passaggio di stato, ad esempio nel passaggio di una sostanza da liquida a gassosa, l’entalpia del sistema è il calore di evaporazione. Invece in un processo di variazione della temperatura l’entalpia è data dalla capacità termica a pressione costante. La definizione di entalpia è:

Una reazione con variazione d’entalpia negativa è esotermica, mentre una reazione con variazione d’entalpia positiva è endotermica.

Calore specifico e entalpia specifica di una miscela aria-vapore

Il calore specifico a pressione costante c_p è la media pesata dei calori specifici dell’aria e del vapore per la miscela considerata. La sua definizione è:

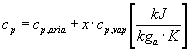
L’entalpia specifica di una miscela aria e vapore è

,

dove h_a è l’entalpia specifica dell’aria secca, mentre h_v è l’entalpia specifica del vapore d’acqua. Assumendo come stato convenzionale a valore nullo di entalpia il gas ideale a T₀=273,15 K (0°C), risulta:

Si assume per l’acqua quale stato convenzionale a entalpia nulla lo stato di liquido saturo a T₀=273,15 K. L’entalpia specifica del vapore d’acqua, dipendendo solo dal valore della temperatura in quanto considerato gas ideale, può essere calcolata con questa relazione:

,

dove r₀ è il valore del calore di vaporizzazione dell’acqua a T=273,15 K.

Calore specifico dell’aria: c_p,a=1 kJ/kg_aK.

Calore specifico del vapore d’acqua: c_p,v=1,9 kJ/kg_vK.

Calore specifico dell’acqua: c_p,ac=4,81 kJ/kg_vK.

Calore di vaporizzazione dell’acqua: r₀=2500 kJ/kg_v.

Entalpia specifica dell’aria umida: h=t+x(2500+1,9t) kJ/kg_a.

L’aria è definita in diversi modi a seconda della sua composizione. Questi sono:

- aria atmosferica, contenente principalmente azoto e ossigeno, ed una miscela di altri gas, tra cui anidride carbonica, vapore acqueo e varie sostanze inquinanti. È l’aria che respiriamo, che è utilizzata negli impianti di condizionamento.

- aria secca, costituita da azoto (circa 78%), ossigeno (circa 21%) e da piccole quantità di gas, come argon, neon, anidride carbonica.

- aria umida, che è una miscela di aria secca e vapore acqueo.

Per definire le grandezze relative all’aria umida occorre considerare che, mentre i gas (N2, O2, Ar, ecc.) che costituiscono l’aria si trovano molto sopra la propria isoterma critica, quindi rimangono allo stato gassoso, invece il vapore d’acqua si trova al di sotto della propria isoterma critica e può diventare liquido (rugiada, nebbia) o addirittura solido (brina). Per l’aria umida valgono le leggi di Dalton: la pressione totale è la somma delle pressioni parziali

le pressioni dei componenti sono proporzionali alle quantità di essi espresse come numero di molecole:

Se a un dato volume d’aria si aggiunge altro vapore acqueo, la pressione parziale di quest’ultimo aumenta. Quando questa pressione parziale raggiunge il valore della pressione di vapore a quella temperatura, si dice che l’aria è satura. A quel punto il vapore acqueo inizia a condensare in forma liquida se la temperatura è superiore al punto di fusione, o sotto forma di cristalli di ghiaccio (neve o brina) se la temperatura è inferiore al punto di fusione. Il rapporto tra la pressione parziale del vapore acqueo e la pressione di vapore a quella temperatura è chiamata umidità relativa. È da sottolineare che l’aria può essere satura solo se è in contatto con acqua liquida (sopra e vicino ad uno specchio d’acqua, quando piove), altrimenti contiene una quantità di acqua (allo stato di vapore) minore della saturazione. Se ne contiene una quantità maggiore, condensa e si separa (nebbia, rugiada).

Esperimento del bicchiere d’acqua

Si tratta di un esperimento che consente di capire meglio i concetti di aria secca e aria umida. Consiste nella disposizione di un bicchiere pieno d’acqua sotto ad una campana al cui interno è presente aria secca a temperatura T costante e pressione p=1 bar. Si nota che, dopo un certo tempo, parte dell’acqua contenuta nel bicchiere è evaporata e il vapore che si è formato ha trasformato l’aria da secca in umida. Il processo continuerà fino a quando il titolo raggiungerà il punto di saturazione.

Esistono due diverse grandezze per indicare la quantità di vapore acqueo presente nell’aria:

- il titolo, definito come rapporto tra massa di vapore e massa di aria secca:

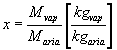
Non è da confondere con il titolo che caratterizza i vapori saturi, definito come

che è un numero compreso tra 0 e 1.

- il grado igrometrico o umidità relativa, grandezza definita come rapporto tra la pressione parziale del vapore acqueo e la pressione del vapore saturo a quella temperatura:

Questa grandezza è compresa tra 0 e 1 e può essere definita in forma percentuale, tramite una moltiplicazione per cento.

Il valore della pressione del vapore saturo dipende dalla temperatura e si ricava dalla seguente tabella:

I valori della pressione del vapore saturo in funzione della temperatura possono essere rappresentati graficamente. Inoltre dall’equazione di Clausius-Clapeyron si ricava un’equazione che approssima i dati sperimentali della tabella:

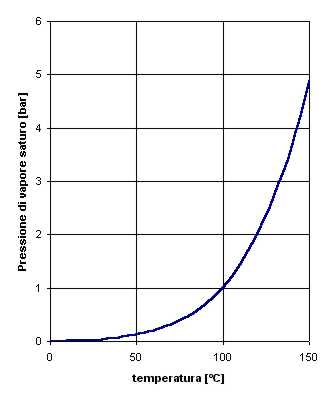
Tra titolo e grado igrometrico esiste una relazione:

dal momento che , dalla definizione di grado igrometrico

e , dalla legge di Dalton,

si ottiene che:

dove n_v e n_a rappresentano rispettivamente il numero di moli di vapore e di aria secca presenti nella miscela di aria umida considerata, e m_v e m_a le masse molari dei due componenti. Con p_tot si intende la pressione totale della massa d’aria umida presa in considerazione e p_s la pressione di saturazione del vapore alla temperatura considerata.

Il valore di x tale per cui j=1 è detto titolo di saturazione.

La temperatura alla quale l’aria diventa satura di vapore acqueo, cioè quando l’umidità relativa è pari al 100%, è detta punto di rugiada. Quando la superficie della Terra di notte si raffredda al di sotto del punto di rugiada, si forma rugiada, se il punto di rugiada è maggiore di 0°C, o si forma brina, se esso è minore di 0°C.

Il diagramma psicrometrico è una rappresentazione grafica delle proprietà dell’aria in varie situazioni. Assmann realizzò per primo il diagramma psicrometrico in relazione alla sua invenzione, lo psicrometro o igrometro. Si struttura in questo modo: sull’asse delle ascisse si trova la temperatura t, mentre sull’asse delle ordinate si trova il titolo x, misurato in g_vap/kg_aria.

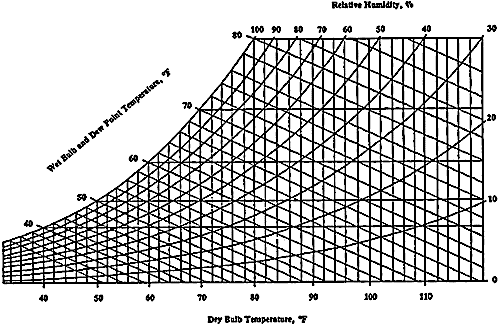
Nel diagramma sono utilizzati tre diversi tipi di misurazione della temperatura:

• temperatura del bulbo secco, cioè dell’aria misurata con un semplice termometro. La scala si trova alla base del grafico e le linee verticali indicano uguali temperature del bulbo secco;

• temperatura del bulbo umido, determinabile facendo passare l’aria sopra un termometro avvolto da un tessuto umido. Questa riflette l’effetto refrigerante dell’evaporazione dell’acqua, che causa una temperatura più bassa rispetto a quella del bulbo secco. La scala si trova lungo la curva in alto a sinistra nel grafico e le linee inclinate indicano uguali temperature del bulbo umido;

• temperatura del punto di rugiada, cioè la temperatura al di sotto della quale l’umidità presente nell’aria condensa. La scala è lungo la curva in alto a sinistra nel grafico e le linee orizzontali indicano uguali temperature del punto di rugiada.

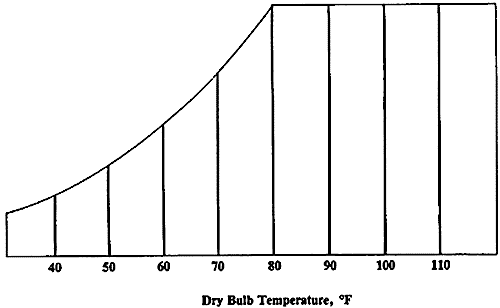
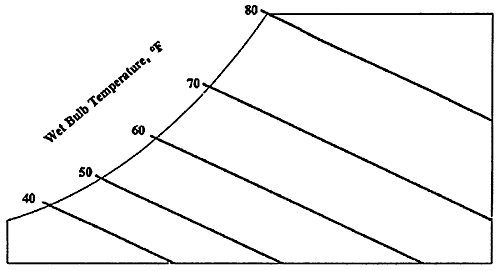
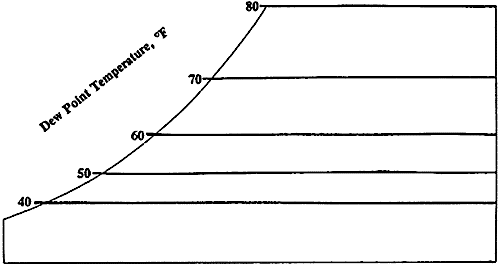
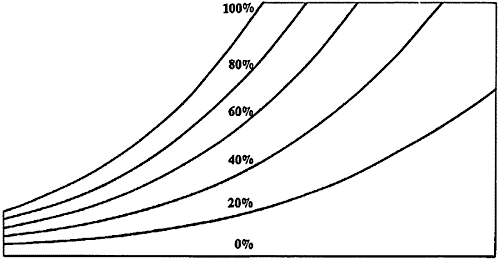
L’umidità relativa, in percentuale, è espressa nel diagramma psicrometrico da linee curve che partono in basso a sinistra ed arrivano in alto a destra. La linea relativa al 100% corrisponde alla scala delle temperature del bulbo umido e del punto di rugiada. Quella relativa allo 0% è invece sulla scala della temperatura del bulbo secco.

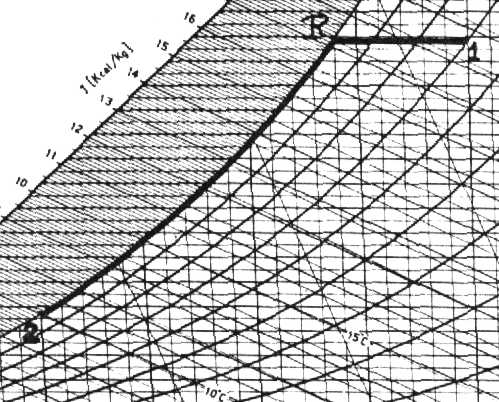
Una massa M=10 kg di aria umida avente grado igrometrico j=0,7, inizialmente alla temperatura di 30°C, viene raffreddata fino alla temperatura di 10°C seguendo la trasformazione indicata in figura. Si determinino la quantità di calore Q da sottrarre alla miscela e la massa d’acqua che condensa. Si supponga che la trasformazione avvenga ad una pressione costante p=1,013 bar.

Dati:

Massa totale: M_tot=10 kg

Temperatura iniziale: t₁=30°C

Grado igrometrico iniziale: j=0,7

Temperatura finale: t₂=10°C

Pressione: p=1,013 bar

Quesiti:

Quantità di calore da sottrarre: Q=?

Massa d’acqua condensata durante il processo: M_cond=?

Risoluzione:

Per capire come avverrà la trasformazione, è necessario osservare il diagramma psicrometrico relativo al problema. Da questo si rileva che la trasformazione avviene in due fasi: nella prima il sistema subisce un raffreddamento, mantenendo il titolo costante fino al raggiungimento della curva di saturazione j=1 (punto R). In questo punto la temperatura è t_R=24°C e viene definita temperatura di rugiada, dal momento che, essendo la miscela già satura, se la si raffredda ulteriormente il vapore d’acqua presente condensa. Durante la seconda fase, il raffreddamento continua fino al raggiungimento di 10°C, quindi la trasformazione R-2 avviene lungo la curva di saturazione. Durante questa, lungo la curva di saturazione, si ha la presenza contemporanea di due fasi in equilibrio termodinamico: aria satura di vapore e acqua.

Dal momento che la trasformazione avviene a pressione costante, dal primo principio della termodinamica risulta dh=dq-dl; non si compie lavoro in quanto semplice raffreddamento, quindi Q=M_a(J₂-J₁).

È necessario determinare la massa d’aria secca M_a presente nella miscela, in quanto le entalpie sono riferite ad un kg di aria secca. Quindi:

ed essendo si ha da cui .

Dalla tabella: ps=0,0424 bar=31,8 mm Hg è la pressione di saturazione del vapore a 30°C.

Nello stato iniziale il titolo della miscela vale:

Noto il titolo x₁, si può ricavare la massa d’aria secca M_a presente nella miscela:

Ora si calcolino le entalpie della miscela negli stati iniziale e finale:

Essendo

Si ha:

Infine:

La quantità di calore scambiata durante la trasformazione è negativa dal momento che viene sottratta al sistema.

In un miscelatore entrano due correnti di miscela d’aria e vapore, una di M₁=1500 kg/h, alla temperatura t₁=5°C e l’altra M₂=3000 kg/h alla temperatura t₂=15°C. I rispettivi titoli sono x₁=4,5 g_V/kg_a e x₂=6 g_V/kg_a. All’uscita sono richieste queste condizioni termoigrometriche: temperatura t₄=22°C e titolo x₄=8 g_V/kg_a. Al fine di ottenere queste condizioni, è necessario fornire una quantità m₃ d’acqua alla temperatura t₃=17°C ed una quantità Q di calore.

Si calcolino:

1. la portata d’aria M₄ in uscita;

2. la portata d’acqua m₃ necessaria;

3. la quantità di calore Q che si deve fornire.

Dati:

M₁=1500 kg /h t₁=5°C x₁=4,5 g_V/kg_a

M₂=3000 kg/h t₂=15°C x₂=6 g_V/kg_a

Quesiti:

a) Portata d’aria in uscita: M₄=?

b) Portata d’acqua necessaria: m₃=?

c) Quantità di calore da fornire: Q=?

Risoluzione:

1. Per il principio di conservazione della massa:

   

   Per le miscele d’aria e vapore acqueo si prende in esame, in genere, la portata d’aria secca; quindi, essendo M la portata della miscela, si ha:

   

   dove M_a è la portata d’aria secca e M_V la portata di vapore. Dalla definizione di titolo:

   

   si ottiene : da cui .

   Il bilancio di massa per il vapore d’acqua è espresso da:

   

   La portata d’aria secca M₄ e quella d’acqua m₃ si determinano dalle due relazioni di bilancio di massa. Si ha:

   

   da cui

   

2. Dal principio di conservazione della massa si ha la portata d’acqua necessaria:

   

3. La quantità di calore Q si calcola con l’utilizzo dell’equazione del bilancio energetico generalizzato per un sistema aperto a più correnti entranti e uscenti in regime stazionario:

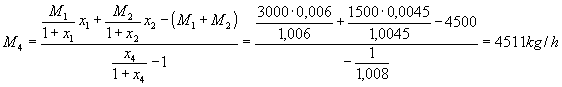
Sostituendo i valori numerici:

Dalle tabelle si ricava il valore dell’entalpia dell’acqua a 17°C:

Sostituendo i valori calcolati nell’equazione del bilancio energetico si ottiene Q:

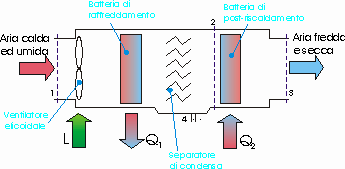
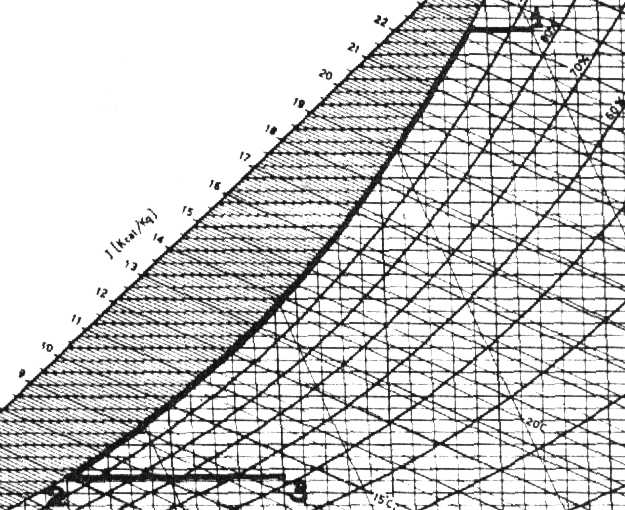
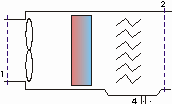
Un ambiente di 470 m³di volume è mantenuto ad una temperatura di 20°C e ad un’umidità relativa del 52,5%. Si consideri che l’aria nell’ambiente viene completamente ricambiata ogni ora e prelevata dall’atmosfera nelle seguenti condizioni: pressione p=1 bar, temperatura t=32°C, umidità relativa j=0,86. Questo avviene mediante un ventilatore che fornisce la potenza utile di 450 W. Come si vede in figura, l’aria passa attraverso una batteria di raffreddamento che ne abbassa la temperatura fino al raggiungimento della condensazione di una parte di vapore in essa presente; il condensato viene raccolto ad una temperatura di 8°C. l’aria satura è poi riscaldata fino a raggiungere le condizioni richieste. La pressione totale si mantiene costante.

Determinare:

1. la temperatura a cui l’aria lascia la batteria di raffreddamento;

2. la quantità di condensato;

1. la quantità di calore sottratto alla batteria di raffreddamento;

2. la quantità di calore fornito alla batteria di post-riscaldamento.

Dati:

Volume: V=470 m³

Pressione: p=1 bar

Temperatura dell’aria esterna: t₁=32°C

Grado igrometrico dell’aria esterna: j=0,86

Temperatura dell’aria interna: t₃=20°C

Potenza fornita dalla ventola: L=0,45 kW

Quesiti:

1. Temperatura dell’aria dopo il raffreddamento: t₂=?

2. Quantità di condensato: M_cond=?

3. Calore sottratto alla batteria di raffreddamnto: Q₁=?

4. Calore fornito alla batteria di post-riscaldamento: Q₂=?

Risoluzione:

1. Dal diagramma psicrometrico si vede che la trasformazione 2-3 avviene a titolo costante; l’aria nel punto 2 è satura, pertanto la sua temperatura corrisponde alla temperatura di saturazione alla pressione parziale del vapore nell’ambiente p_s3=0,02336 bar.

   da cui

   

   Dalla tabella 1 si ricava la temperatura t₂ in funzione della pressione del vapore:

   t₂=10°C

2. Per determinare la quantità d’acqua condensata occorre conoscere il titolo in 1 ed in 2 ed utilizzare il bilancio di massa riferito al vapore d’acqua.

   

   Tenendo presente che nel punto 1 e nel punto 3 la temperatura vale rispettivamente 32°C e 20°C, si ricavano i titoli x₁ e x₃ dell’aria in ingresso e in uscita dal condizionatore:

   

   

   Il bilancio di massa per il vapore d’acqua, riferito al kg di aria secca, risulta:

   

   Dall’equazione dei gas perfetti

   

   si ricava la portata di aria secca:

   

   Per calcolare la portata di massa condensata in un’ora è sufficiente moltiplicare la massa d’aria per la differenza dei titoli:

   

3. Utilizziamo l’equazione del bilancio dell’energia a regime stazionario, considerando positive le masse uscenti:

   

    

   dove h_cond rappresenta l’entalpia specifica della massa condensata;

   

   ora calcoliamo le entalpie J₁ e J₂:

   

   

   L’entalpia specifica dell’acqua condensata è

   

   dove c è il calore specifico per l’acqua ed è pari a 4,18 kJ/kgK, quindi

   

   Sostituendo nell’equazione del bilancio energetico:

   

   La quantità di calore Q risulta negativa in quanto sottratta al sistema. Nel sistema non si è tenuto conto dell’energia scambiata sotto forma di calore attraverso il ventilatore.

4. Applicando ancora una volta il bilancio energetico, tra le sezioni 2 e 3, si ottiene la potenzialità termica della batteria di post-riscaldamento:

e quindi:

Sostituendo nell’equazione del bilancio energetico, si ha: