Fluidodinamica
Per introdurre il
concetto di Fluidodinamica dobbiamo innanzitutto dire che le sostanze si
possono suddividere in tre forme di aggregazione:
_ stato solido
_ stato liquido
Stato solido: è lo stato
di aggregazione in cui non cambiano nè il volume nè la forma.
Stato liquido: è lo stato
di aggregazione in cui cambia la forma (i liquidi, infatti, assumono la forma
del contenitore nel quale sono contenuti) ma resta invariato il volume (sono
difficilmente comprimibili).
Stato aeriforme: è lo stato
di aggregazione in cui cambiano sia la forma che il volume (hanno una
comprimibilità più elevata rispetto ai liquidi).
Tutte queste categorie
sono delle semplificazioni, infatti ci sono dei liquidi che cambiano il loro
volume, anche se solo in minima parte.
Tra questi tre stati che
caratterizzano le sostanze quelli di cui si occupa la fluidodinamica sono: lo Stato liquido e lo Stato aeriforme (anche se noi ci occuperemo solo
dello stato liquido).
Possiamo
quindi definire la Fluidodinamica
come quella scienza, che
fa parte della meccanica, che tratta il moto dei fluidi, tale moto si divide
in:
Moto interno: che studia il moto dei fluidi
all’interno dei condotti (tubi, canali etc.)
Moto esterno: che studia il moto dei fluidi all’esterno dei condotti.
Una cosa
molto importante da tener presente è che le equazioni della Fluidodinamica
valgono per entrambe i moti.
Il fenomeno
più evidente nel moto dei fluidi è il trascinamento,quando un fluido scorre su
di una superficie le particelle del fluido sono soggette ad un Attrito viscoso.
La viscosità oltre a rappresentare la difficoltà che uno strato ha nello scorrere su di
un altro strato, rappresenta una grandezza che è legata al concetto di
forza e di velocità. Se prendiamo ad
esempio l’acqua e l’olio che scorrono su di una superficie, sicuramente l’acqua
ha una velocità maggiore rispetto all’olio, in quanto l’acqua al contrario
dell’olio ha meno forze che si oppongono al suo moto.
Numericamente la
viscosità è espressa dal Coefficiente di viscosità :μ
, che è definito dalla seguente espressione:
![]() (1)
(1)

Un’altra unità di misura
utilizzata per la viscosità è il Poise:
![]() (2)
(2)
Attenzione!
Se mi viene dato il valore in Poise per ricondurmi al S.I. devo dividere tale valore per 10.
Legato al
concetto di viscosità troviamo quello di tensione.
Per capire meglio questo
concetto aiutiamoci con una rappresentazione grafica, disegnamo un sistema con
due cilindri, uno interno all’altro. Tra questi due
cilindri inseriamo il liquido che vogliamo studiare. Se ruoto il cilindro
esterno, ruoterà anche quello interno, per tenerlo fermo devo quindi applicare
una forza che mi tenga fermo il cilindro interno. 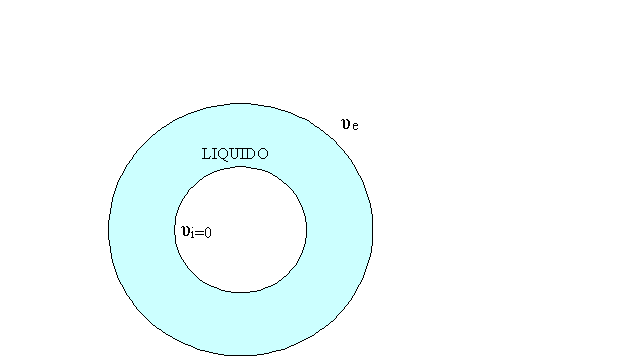
Fig.1 - Visione dall’alto
dei due cilindri.
Se prendo in considerazione una minima parte dei due cilindri posso considerare le due superfici quasi parallele e mi accorgo che : le particelle vicino alla superficie interna restano ferme, mentre quelle a ridosso della superficie esterna partecipano al moto del cilindro (tutto questo si può osservare in figura 2).
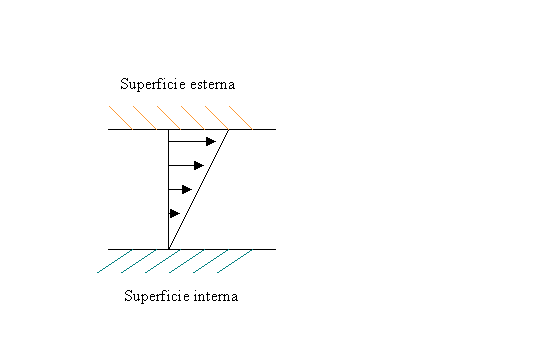
Fig.2- Particolare dei due cilindri.
Per ogni unità di
superficie mi si verrà a creare una tensione.

τ rappresenta la tensione e ha come unità di misura il
Pascal. Tale unità di misura si ottiene facilmente:
![]() (4)
(4)
La legge di
Newton dice che: la tensione è data dal rapporto tra la variazione di velocità
e il valore dell’ascissa moltiplicata per la viscosità.
![]() (5)
(5)
Da queste
equazioni ricaviamo che , la tensione aumenta con l’aumento della viscosità. La
legge di Newton, al contrario, definisce la variazione di viscosità μ
costante, in realtà non tutti i fluidi sono newtoniani.
Classificazione
dei fluidi:
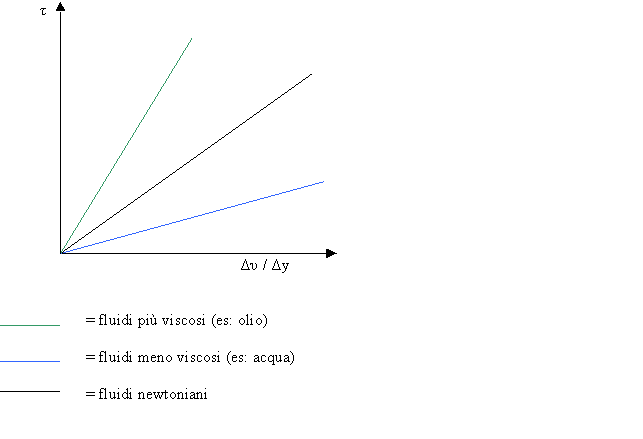 Fig.3-Grafico sulla viscosità dei
fluidi.
Fig.3-Grafico sulla viscosità dei
fluidi.
In base a quanto abbiamo affermato possiamo classificare i fluidi secondo tre ben distinte categorie:
_ fluidi dilatanti
_ fluidi newtoniani
_ fluidi pseudoplastici
Possiamo inoltre tracciare i grafici di tali categorie (fig.4-5-6), che ci rendono più evidenti le differenze che si possono riscontrare tra i vari tipi di fluidi ( tali differenze consistono nella variazione di tensione da applicare ad un fluido per farlo spostare).
I fluidi dilatanti, nei quali la tensione, cioè la forza da applicare per far muovere il fluido, aumenta con l’aumento della velocità, sono ad esempio gli amidi ed i grassi utilizzati per la produzione alimentare.
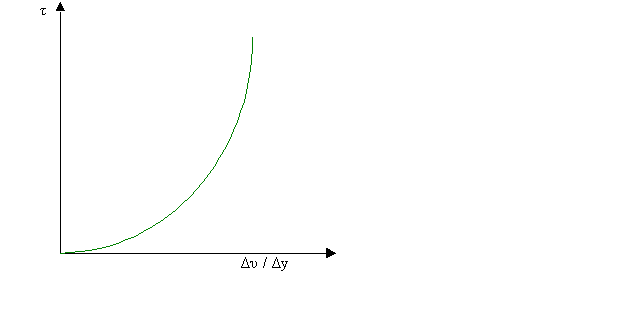 Fig.4-Grafico dei fluidi
dilatanti.
Fig.4-Grafico dei fluidi
dilatanti.
I fluidi newtoniani, nei quali lo sforzo da applicare per muovere il fluido è costante. Alcuni esempi possono essere benzina acqua.
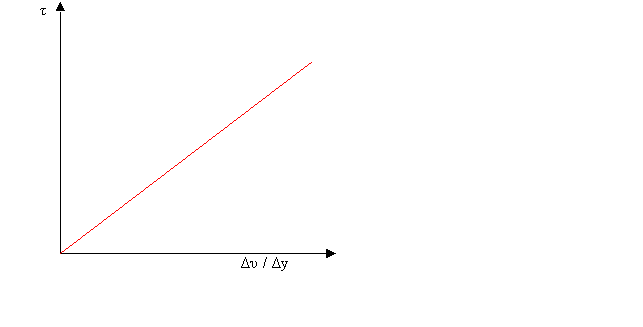 Fig.5-Grafico dei fluidi
newtoniani.
Fig.5-Grafico dei fluidi
newtoniani.
Fluidi pseudoplastici nei quali gli sforzi da applicare diminuiscono con l’aumento della velocità. Un esempio sono le gelatine.
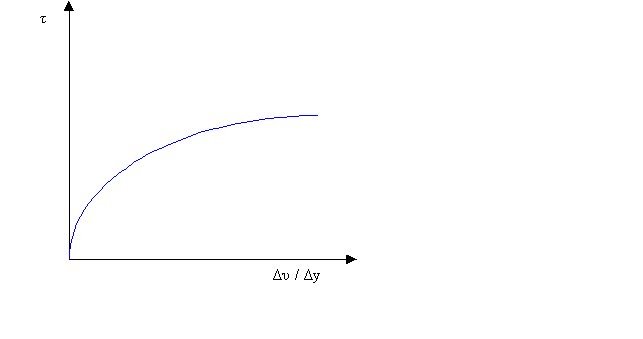 Fig.6-Grafico dei fluidi
pseudoplastici.
Fig.6-Grafico dei fluidi
pseudoplastici.
Altre proprietà del fluidi:
La massa volumica ρ [m³/Kg] è la massa m [Kg] della sostanza contenuta nell’unità di volume V [m³]:
![]() (6)
(6)
Il reciproco della massa volumica è il volume massico v[m³/Kg], volume V [m³] riferito all’unità di massa m[Kg], espresso da:
![]() (7)
(7)
La densità è il rapporto
tra la massa volumica della sostanza e la massa volumica di una sostanza di
riferimento ed è quindi un numero puro, privo cioè di dimensioni. Nel caso dei
solidi e dei liquidi la massa di riferimento è rappresentata dalla massa
volumica ρ![]() dell’acqua a 4° C:
dell’acqua a 4° C:
![]() (8)
(8)
Per comprimibilità di un fluido si intende la variazione della sua massa volumica in conseguenza di una variazione della pressione.Tutti i fluidi reali (si definisce fluido reale un fluido in cui occorre tener presente la viscosità nei calcoli) sono comprimibili, cosicché la loro massa volumica cambierà al variare della pressione. Tuttavia, quando la variazione della massa volumica al variare della pressione è così piccola da potersi ritenere trascurabile, allora il fluido può essere trattato come incomprimibile: è questo il caso dei liquidi. Al contrario, i gas possono essere compressi con estrema facilità e, fatta eccezione per variazioni di pressione e quindi di massa volumica molto modeste, saranno considerati comprimibili.
Quando il fluido può essere considerato incomprimibile, come nel caso delle macchine idrauliche, la massa volumica ρ è costante: l’equazione che afferma questo è:
![]() (9)
(9)
e viene chiamata equazione di stato perché descrive lo stato di quel particolare fluido.
La viscosità cinematica v è il rapporto tra viscosità dinamica μ e massa volumica ρ, si misura in m²/s ed è chiamata così perché non compare più la massa:
![]() (10)
(10)
Un’unità di misura usata in passato era il centistokes pari a 1mm²/s.
Nella tabella che segue si possono ritrovare i valori tipici della viscosità dinamica μ; della massa volumica ρ e della viscosità cinematica v di otto fluidi alla pressione atmosferica di 101,32 Kpa e alla temperatura di 20° C.
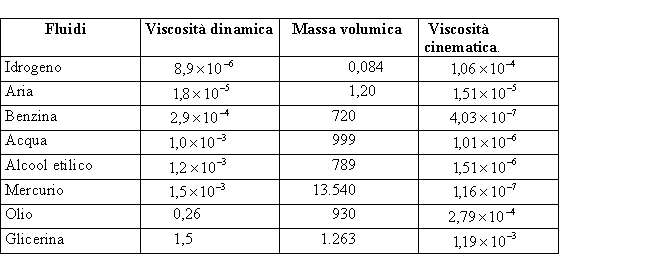
Fig.7-Tabella
con alcuni valori tipici di otto fluidi.
Moto dei fluidi:
Il movimento di un tipo
di fluido può variare da punto a punto e da istante a istante. Il moto si dice uniforme se la velocità in
un dato istante, si mantiene identica in intensità e direzione in ciascun punto
del fluido. Se, al contrario, la velocità in un determinato istante varia da
punto a punto, il moto viene definito non
uniforme. Il moto si dice stazionario
quando tutte le condizioni in ciascun punto della corrente rimangono costanti
rispetto al tempo, pur potendo variare in punti diversi: quando cioè le
principali grandezze che caratterizzano il moto del fluido (velocità, pressione
e sezione trasversale del flusso) possono variare da punto a punto ma non
cambiano con il tempo. Se, al contrario, in un dato punto, le condizioni di
moto cambiano al variare del tempo, allora il moto si dice non stazionario. Il moto stazionario (o non
stazionario) e il moto uniforme (o non uniforme) possono esistere
indipendentemente l’uno dall’altro; sono quindi possibili quattro combinazioni.
Così un liquido che si muove con portata costante, in un condotto lungo e
diritto di sezione costante, dà luogo a un moto stazionario
uniforme (la velocità del liquido infatti in ogni punto del condotto e
in ogni istante è la stessa); il moto di un liquido con portata costante in un
condotto conico è un moto stazionario non uniforme (essendo
la portata costante, la velocità del liquido si mantiene la stessa ad ogni
istante in un determinato punto, ma varia da punto a punto nel procedere lungo
il condotto in quanto varia il diametro della sezione). Al variare della
portata del liquido i due casi precedenti diventano rispettivamente esempi di moto non stazionario uniforme (nel condotto a sezione
costante la velocità varia da istante a istante in quanto cambia la portata, ma
varia da punto a punto nel procedere lungo l’asse del condotto, in quanto la
sezione rimane costante) e di moto non stazionario e
non uniforme (è il condotto conico in cui la velocità del liquido varia,
da istante a istante, per la variazione della portata e, da punto a punto lungo
l’asse, in quanto varia la sezione del condotto).
Nel funzionamento delle
macchine possiamo distinguere un periodo iniziale transitorio,
solitamente molto breve, caratterizzato da una sensibile variazione delle
grandezze, in funzione del tempo, seguito da un periodo a regime, in cui le principali grandezze che individuano il moto
del fluido si sono sensibilizzate: si sono raggiunte così le condizioni di moto
stazionario.
Nel caso del moto non
uniforme, si verificano, da punto a punto, delle variazioni del campo di moto,
in modo tale che velocità, pressioni e altri fattori variano rispetto alle tre
coordinate spaziali. Ma la maggior parte dei problemi pratici può essere
trattata come se la variazione delle principali grandezze caratterizzanti il
moto del fluido avvenisse secondo una sola direzione. Definiamo così corrente unidimensionale o monodimensionale
quella in cui i principali parametri quali velocità, pressione e quota
variano soltanto lungo la direzione del flusso e non da punto a punto di una
data sezione trasversale normale al flusso. In pratica ciò equivale a
considerare tutte le proprietà del fluido – pressione, velocità e quota –
uniformi su una data sezione trasversale.
Nel caso particolare del
fluido incomprimibile quale quello trattato nella idrodinamica, occorre
considerare l’equazione di stato che afferma che la sua massa volumica ρ
rimane costante.
Esperimento
di Reynolds:
Iniettando del colore
all’ingresso di un tubo di vetro trasparente nel quale fluisce dell’acqua
proveniente da un serbatoio (come si può vedere in figura) si trova che se il
serbatoio è riempito con poca acqua, le particelle d’acqua che formano il
cosiddetto filetto fluido,si muovono per linee
parallele.
.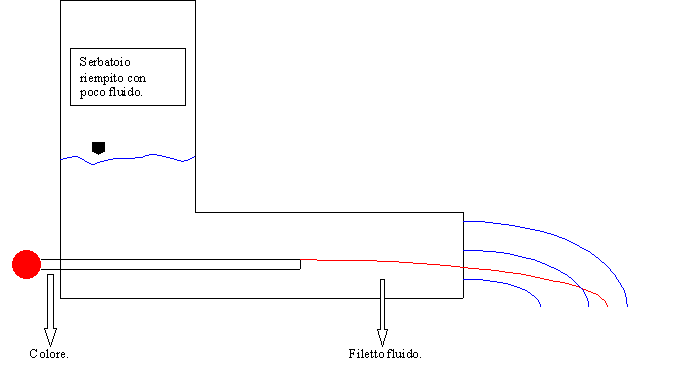
Fig.8- Esperimento di
Reynolds ( caso del serbatoio con poco fluido)
Se al contrario il
serbatoio è riempito con molta acqua si raggiunge una condizione per cui il filetto fluido dapprima inizia ad oscillare, e
successivamente, a rompersi mescolandosi completamente con il resto del fluido
(come si può notare nella figura 9).
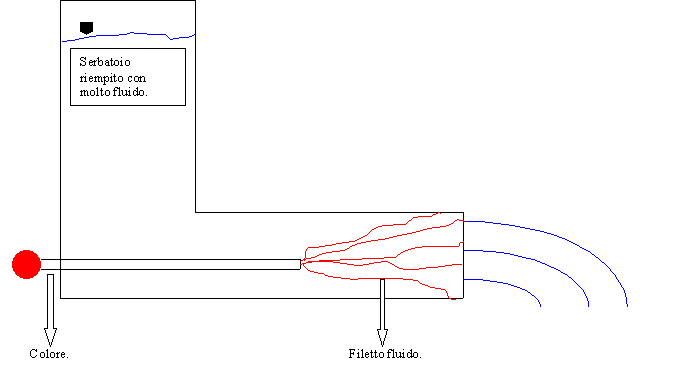
Fig.9-Esperimento
di Reynolds (caso del serbatoio riempito con molto fluido).
Il moto del “filetto
fluido” dipende dalla quantità di liquido contenuta nel serbatoio. Si possono
così avere due diversi tipi di moto:
Moto laminare: nel quale i filetti fluidi all’interno del
serbatoio non si mescolano con il resto del liquido. Ogni singola particella,
infatti, continuerà il suo moto parallelamente al serbatoio, non si verificano
quindi turbolenze o rimescolamenti.
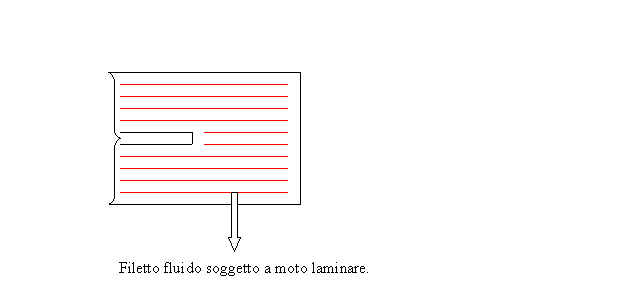
Fig.10-Rappresentazione del moto laminare.
Moto turbolento: nel quale si originano turbolenze. Ogni
particella assume una traiettoria caotica e all’interno del serbatoio si
verifica un forte rimescolamento.
 Fig.11-Rappresentazione del moto
turbolento.
Fig.11-Rappresentazione del moto
turbolento.
Il numero di Reynolds
R è il parametro che ci dice quando siamo in presenza di moto laminare e
quando di moto turbolento. Esso è funzione della massa volumica ρ,
della velocità v, della
viscosità dinamica μ del fluido e di una lunghezza caratteristica l del
sistema fisico considerato (potrebbe essere il diametro del canale in cui
scorre il fluido):
![]() (11)
(11)
Il numero di Reynolds è un numero puro
risultato del rapporto tra grandezze aventi le stesse dimensioni:
![]() (12)
(12)
Esso può anche essere espresso in funzione della viscosità cinematica:
![]() (13)
(13)
Da esperienze effettuate facendo scorrere liquidi diversi in tubi diritti
di vario diametro, è stato calcolato il numero di Reynolds, assumendo come
lunghezza caratteristica il diametro del tubo e, come velocità, la velocità
media del liquido. Si è visto che per valori del numero di Reynolds al di sotto
di 2100 il moto è laminare, tra 2100 e 4000 vi è una zona di transizione tra i
due regimi, mentre al di sopra di 4000 il moto è turbolento. Questi valori del
numero di Reynolds si applicano soltanto al moto ei fluidi nei condotti, ma
altri valori di R possono essere ricavati per altri tipi di flusso,
come, ad esempio, quello lungo la paletta di un compressore.
Definiamo come numero di Reynolds critico quel numero di Reynolds in
corrispondenza del quale si verifica la transizione da regime laminare a regime
turbolento.
Esercizio:
Possiamo fare un esempio per capire meglio come si può calcolare il numero
di Reynolds:
Se abbiamo un tubo di diametro di 50,8 mm all’interno del quale scorre
ammoniaca alla velocità di 21,3 m/s. L’ammoniaca ha una viscosità di ![]() e una densità di
e una densità di ![]() .Qual è il numero di Reynolds?
.Qual è il numero di Reynolds?
![]()
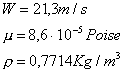
![]()
Conservazione
della massa:
Con la sola eccezione dei
processi nucleari, la materia non può essere né creata né distrutta.Applichiamo
questo principio, detto di conservazione della massa,
al moto di un fluido in un condotto, nel quale individuiamo la sezione 1 come
la sezione di ingresso del fluido e la sezione 2 come la sezione d’uscita.
Facciamo anzitutto l’ipotesi che il moto sia stazionario: in tal caso, la massa
di fluido che si trova tra le due sezioni considerate del condotto rimane
costante (non abbiamo cioè né accumuli né fughe di fluido, ma la quantità di
fluido che entra è uguale alla quantità di fluido che esce). Immaginiamo poi
che la velocità del fluido all’interno del condotto sia, per l’ipotesi
unidimensionale, uguale su tutti i punti di una stessa sezione trasversale e
diretta normalmente a questa. In altre parole, la velocità del fluido è diretta
normalmente alla sezioni di ingresso 1 e di uscita 2 (figura 12); il fluido può
quindi entrare da 1 e uscire da 2, ma non può né entrare né uscire dalla
superficie laterale, poiché la sua velocità è diretta tangenzialmente alle
pareti del condotto.
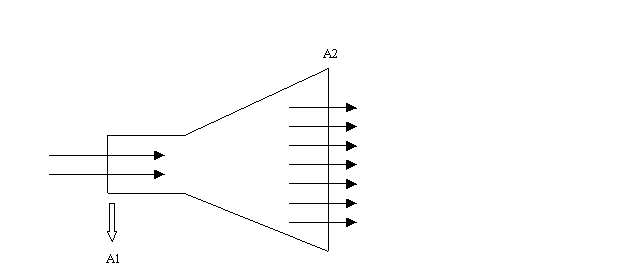
Fig.12-Rappresentazione del moto del fluido.
Sotto le due ipotesi di
moto stazionario (la quantità di fluido che entra nel condotto è uguale a
quella che esce) e di corrente unidimensionale (la velocità del fluido - cioè
la velocità media che abbiamo definito precedentemente – è costante sulle
sezioni trasversali del condotto ed è diretta normalmente a queste) possiamo
scrivere che la portata in massa m vale:

Nell’equazione (14) che
prende il nome di equazione unidimensionale di
continuità, m è la portata in massa di fluido che passa nel
condotto: tale portata m deve essere uguale alla portata di fluido che
entra nella sezione 1, di area trasversale ![]() con velocità
con velocità ![]() diretta normalmente a questa sezione e con massa volumica
diretta normalmente a questa sezione e con massa volumica
![]() ;la portata m deve essere poi uguale alla portata di
fluido che esce dalla sezione 2, di area trasversale
;la portata m deve essere poi uguale alla portata di
fluido che esce dalla sezione 2, di area trasversale ![]() con velocità
con velocità ![]() diretta normalmente
ad
diretta normalmente
ad ![]() e con massa volumica
e con massa volumica ![]() .
.
Nel caso di un fluido
incomprimibile come l’acqua, la massa volumica non cambia nel passare dalla
sezione 1 alla sezione 2; ciò equivale a dire che la portata in volume è
costante.
Energia di un
fluido in movimento:
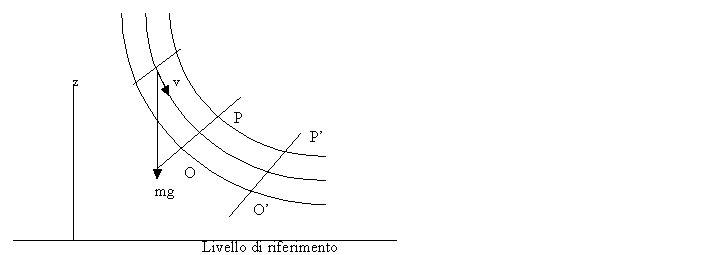
Allo stesso modo di
quanto avviene per un corpo solido, l’elemento di fluido di massa m che
si muove lungo un condotto (come si vede in figura13) possiede un’energia potenziale
(originata dal fatto di trovarsi a una determinata quota z valutata
rispetto ad un piano di riferimento) e un’energia cinetica (determinata dalla
sua velocità v).

L’energia potenziale è quindi data dal prodotto della forza peso mg per lo spostamento z, che è la distanza del baricentro dell’elemento di fluido considerato rispetto al livello di riferimento. Nota la velocità v dell’elemento di fluido di massa m (figura13), l’energia cinetica è espressa da:
![]()
e, in unità di misura, da:
![]()
Oltre a considerare le due energie appena citate,
dobbiamo tenere presente che l’elemento di fluido, che si sposta in modo
stazionario dalla sezione OP alla sezione O’P’ , compie anche un lavoro in
virtù della sua pressione. Infatti sulla sezione trasversale OP la pressione
genera una forza che, spostandosi la sezione in avanti a seguito del movimento
del fluido, genera un lavoro. Se indichiamo con p la pressione nella
sezione trasversale OP di area A, la forza F che si esercita su
questa sezione è pari a F=pA. Lo spostamento dell’elemento di
massa m, che si muove lungo un filetto fluido, dalla sezione OP alla
sezione O’P’ è pari al rapporto tra volume V e area A; il volume V
a sua volta si ricava come rapporto tra massa m e massa volumica p.
![]()
Il prodotto della forza pA per lo spostamento (m/p)A è il lavoro del flusso, chiamato di solito energia di pressione, effettuato dalla pressione per spingere per spingere la massa di fluido attraverso la sezione:

L’energia di pressione si misura in J al pari delle altre due energie potenziale e cinetica considerate prima:
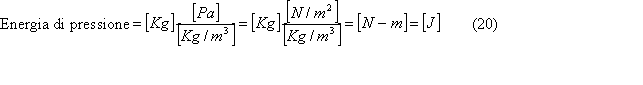
Il concetto di energia di pressione non è di facile comprensione. Nella meccanica dei corpi solidi, un corpo è libero di cambiare la sua velocità, nel senso che la sua energia potenziale può essere liberamente convertita in energia cinetica allorché la quota diminuisce. Non così in una corrente di fluido, dove la velocità deve soddisfare l’equazione di portata, funzione della sezione trasversale della corrente. Se ad esempio, un fluido incomprimibile come l’acqua scorre in un tubo a sezione costante inclinato, la sua velocità non può cambiare. Perciò l’energia potenziale che, al diminuire della quota, non riesce a convertirsi in energia cinetica, appare sotto forma di aumento di pressione.
Conservazione
dell’energia. Equazione di Bernoulli:
Facciamo l’ipotesi che, nel moto del fluido incomprimibile, non vi siano perdite di energia dovute agli attriti. Allora, per il principio di conservazione dell’energia, la somma delle tre forme di energia (potenziale, cinetica e di pressione) espresse dalle equazioni (15)-(16)-(17) , è una costante; l’energia totale cioè rimane costante, anche se la ripartizione tra le diverse forme di energia può variare a mano a mano che il fluido si sposta lungo il condotto. Possiamo perciò scrivere:
![]() (21)
(21)
dove:


![]()
Più spesso si considera un’energia riferita all’unità di massa oppure all’unità di peso: si indica con e l’energia totale per unità di massa e con H l’energia totale per unità di peso; si passa da e a H moltiplicando quest’ultimo per l’accelerazione di gravità g:
![]() (22)
(22)
Dividendo l’equazione (21) per la massa m, si ottiene l’espressione del principio di conservazione dell’energia massica (per unità di massa):
![]() (23)
(23)
Dividendo invece l’equazione (21) per la forza peso mg (prodotto della massa m per l’accelerazione di gravità g), si ottiene l’espressione della conservazione dell’energia in termini di energia riferita all’unità di peso:
![]() (24)
(24)
L’unità di misura dei singoli membri dell’equazione (24) è espressa da J (joule, unità di misura dell’energia oppure del lavoro) diviso per N (newton, unità di misura della forza; il peso è una forza)o anche, più semplicemente, da m (metri), in quanto, essendo il lavoro dato dal prodotto della forza per la lunghezza, quando si divide un lavoro per una forza si ottiene una lunghezza. E’ per questo che ciascun membro dell’equazione (24) viene indicato con il nome di altezza (è infatti l’altezza di una colonna di fluido espressa in metri)oppure, più spesso, di carico e precisamente:
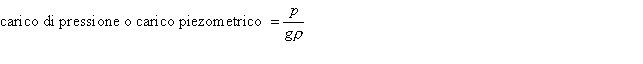

![]()

carico totale del fluido o anche carico idraulico totale =H
L’equazione (24) è l’equazione di Bernoulli : essa dice che, nel moto stazionario di un liquido senza attrito, l’energia totale H per unità di peso rimane costante, anche se la distribuzione tra le diverse forme di energia può variare da punto a punto. L’equazione (24), scritta tra le due sezioni 1 e 2 del condotto (figura 13), diviene:

o più semplicemente:
![]() (26)
(26)
Essendo infatti il carico idraulico totale H costante, il valore che questo assume sulla sezione 1, deve essere uguale al valore che esso ha sulla sezione 2.Possiamo adesso riscrivere l’equazione (25), precisando i valori che pressione, velocità e quota assumono sulle sezioni considerate (la massa volumica ρ rimane invariata in quanto , trattandosi di un fluido incomprimibile, essa assume lo stesso valore sulle due sezioni):
![]() (27)
(27)
Portando tutti i termini al secondo membro, si vedono le tre diverse differenze che compaiono nell’equazione di Bernoulli:
![]() (28)
(28)
L’equazione (26) è stata scritta nell’ipotesi che tra le sezioni 1 e 2 non venga fornita energia al fluido né gliene venga sottratta. Si potrebbe fornire energia al fluido introducendo tra le due sezioni una pompa; parimenti potrebbe essere sottratta energia come lavoro perso per superare gli attriti che si oppongono al moto del fluido reale, oppure come lavoro effettuato dal fluido in una turbina. L’equazione di Bernoulli può essere così generalizzata in tre casi:
Caso
del serbatoio:
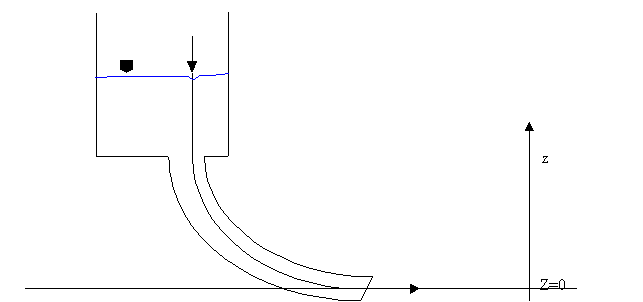
Fig.14-Rappresentazione del caso del serbatoio.
In tal caso l’equazione di Bernoulli diventa:
![]()
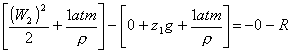 (29)
(29)
<0
Caso
del tubo a sezione costante:
E’ il caso in cui si verifica un incremento di pressione.
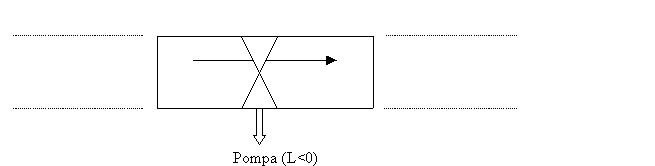
Fig.15-Rappresentazione del caso del tubo a sezione costante.
In questo caso l’equazione di Bernoulli diventa:
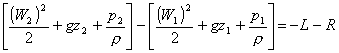 (30)
(30)
Sapendo
che :![]()
L’equazione si semplifica e ottengo:
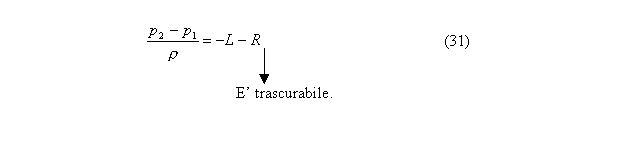
Caso
del rubinetto parzialmente chiuso:
E’ il caso in cui si verifica una diminuzione di pressione.
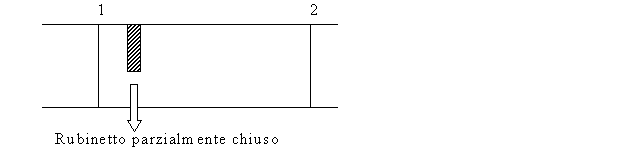
Fig.16-Rappresentazione del caso del rubinetto parzialmente chiuso.
In questo caso l’equazione diventa:
![]() (32)
(32)