Esercizio n° 1

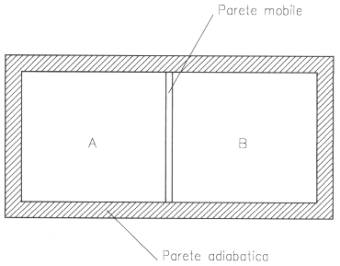
Figura 1

Problema:

In un contenitore adiabatico, come quello rappresentato in Figura 1 sono presenti due sistemi separati da una parete che consente la miscelazione delle due parti.

Il sistema A contiene vapore saturo d’acqua: M_A= 1Kg, p_A= 9,8 bar, x_A= 0,1.

Il sistema B contiene un liquido: M_B= 2Kg, p_B= 0,98 bar, x_B= 0,5.

Scopo del problema:

Ricavare i valori finali della miscela ottenuta, che si troverà in un punto intermedio tra A e B, quindi p_F, x_F, t_F.

Risoluzione del problema:

Si supponga che il contenitore abbia al suo interno gas perfetto, quindi aria.

Si scrivano le equazioni di conservazione della massa e dell’energia, inoltre si scriva l’equazione di conservazione del volume, altrimenti le equazioni non sarebbero sufficienti per la risoluzione del problema.

Si consideri il diagramma (p-v), dove si può notare che all’interno della zona di equilibrio tra liquido e vapore, racchiusa dalla curva limite di Andrews, i cambiamenti di stato tra liquido e vapore hanno luogo gradualmente (Fig. 2).

Nel caso A avremo una pressione p alta e di conseguenza un titolo x basso, quindi il punto sarà posto più vicino all’asse delle ordinate; nel punto B avremo una pressione p inferiore e un titolo x più alto, di conseguenza il punto sarà più vicino all’asse delle ascisse e più lontano dall’asse delle ordinate.

Chiamiamo con F la situazione finale, quindi la miscelazione.

Equazione sulla Conservazione della massa: il sistema è chiuso la massa si conserva, di conseguenza la massa finale vale

M_F = (1.01)

M_i indica la massa dei sistemi presenti nel contenitore, la sua unità di misura è: Kg.

Equazione sulla Conservazione del volume: il volume del contenitore nel punto F rimane invariato.

V_F = = (1.02)

v_F è definito come volume specifico finale, la sua unità di misura è: m³.

I volumi totali V_i sono stati scritti in termini di massa e di volume specifico.

Si ricava il volume iniziale, cioè il volume del contenitore:

v_i = (1.03)

v_i definisce il volume specifico di i, la sua unità di misura è .

x_i è il titolo del sistema i.

v_li indica il volume del sistema i.

v_di è definito come il volume differenziale di i, cioè la lunghezza del segmento sotteso alla curva di Andrews.

Di conseguenza aumentando la pressione, il volume differenziale (cioè la differenza tra il volume occupato dal liquido e dal vapor saturo, con la stessa massa) tende ad aumentare.

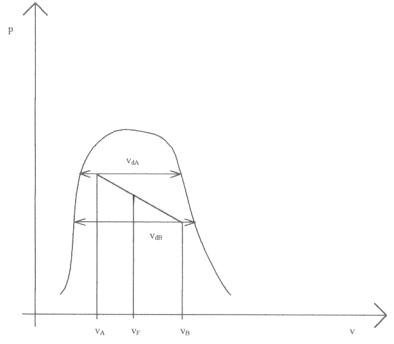
Figura 2 Diagramma (p-v) del vapore.

Dalle tabelle si ricavano i valori di v_li e v_di.

Aumentando la pressione il volume del liquido in B aumenta.

Si ricava il volume specifico finale dalla (1.2) e vale

v_F = (1.04)

Ora si conosce il volume specifico di F e lo si può tracciare nel grafico, quindi posso tracciare la retta sulla quale si posiziona il punto F che soddisfa tutte le equazioni sul bilancio energetico.

Equazione sulla Conservazione dell’energia interna totale:

U_F – (U_A + U_B ) = Q – L = 0 (1.05)

U_i indica l’energia interna dei sistemi i.

Essendo un contenitore chiuso e adiabatico, non c’è alcun scambio di calore e di lavoro, perché le superfici sono rigide.

Tramite questa equazione si può ricavare lo stato fisico finale del sistema.

(1.06)

u_i indica l’energia interna specifica, la sua unità di misura è: .

in questo modo si esprime la (1.5) in termini di grandezze specifiche.

u_i lo si calcola con le formule relative ai vapori e vale

u_i = (1.07)

r_i lo si ricava dalle tabelle termodinamiche.

Dall’equazione sulla conservazione dell’energia interna totale si ricava che:

u_F = (1.08)

Si conosce v_F e u_F, ora rimane da trovare x_F; le tabelle forniscono u_l, x, r, p.

Dato che conosco quanto vale u_F lo si può scrivere in altra forma

u_F = (1.09)

Conoscendo la pressione p_F e il volume V_F si ricava x_{F e vale}

x_F = (1.10)

Per tentativi assegno p_F e attraverso le tabelle si ricava x_F in modo che venga soddisfatta l’energia interna specifica u_F nota.

Calcoli:

Dalla (1.01): M_F = 1 + 2 = 3 Kg

Dalla (1.03): v_A = 0,001126 +0,1 * 0,1969 = 0,0208

v_B = 0,001043 + 0,5 * 1,724 = 0,863

Dalla (1.04): v_F = = 0,5823

Si trasformi la pressione da bar a Pascal: p_A = 9,8 * 10⁵ = 980 KPa

p_B = 0,98 * 10⁵ = 98 KPa

Dalla (1.07): u_A = 759 + 0,1 * (2018 – 980 * 0,1969) = 941

u_B = 415 + 0,5 * (2259 – 98 * 1,724) = 1460

Dalla (1.08): u_F = = 1287

Assegnando p_F = 284 KPa, x_F risulta pari a 0,94 di conseguenza u_F sarà uguale a 2425 , ma il valore ottenuto è troppo alto quindi si procede assegnando una pressione p più bassa.

pF	xF	uF
284	0,94	2425
196	0,65	1820
147	0,49	1472
118	0,4	1260

Quest’ultimo valore si avvicina maggiormente al valore noto di uf, quindi il problema è terminato.

Esercizio n° 2

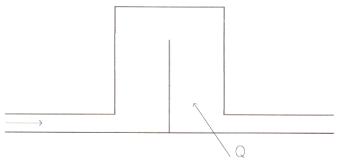
Figura 3

Problema:

Al contrario dell’esercizio precedente, ora il sistema è aperto, quindi si può assimilare a grandi linee a una caldaia. Questo contenitore è dotato di un tubo di ingresso e un tubo di uscita.

L’acqua entra nel sistema a una temperatura di 60° C, mentre il vapore che ne esce ha una temperatura di 300° C; il processo avviene a una pressione di 40 bar. (Fig. 3)

Scopo del problema:

Si vuole calcolare il calore necessario che serve per produrre un Kg di vapore.

Risoluzione del problema:

Consideriamo il diagramma (p-v) per capire meglio la situazione. (Fig. 4)

La temperatura di ebollizione a 40 bar è di 250°C.

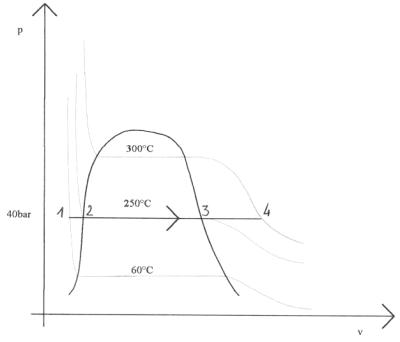
Figura 4 Diagramma (p-v) del vapore.

Equazione dell’Energia riferita al sistema aperto:

(2.01)

Dove l indica il lavoro tecnico, e in questo caso vale 0, q definisce il calore fornito.

Con Δh si vuol indicare la differenza tra l’entalpia specifica uscente e quella entrante.

Dalla (2.01) si ricava q

q = h₄ – h₁= (h₄ – h₃)+(h₃ – h₂)+(h₂ – h₁) (2.02)

Le differenze di entalpia specifica tra i vari punti si trovano nel seguente modo:

h₂ – h₁ = c_l * (T₂–T₁) (2.03)

h₃ – h₂ = r (2.04)

h₄ – h₃ = c_p * (T₄–T₃) (2.05)

c_l (vale 1Caloria) , r (calore di vaporizzazione e varia in funzione della pressione), c_p (riferito al vapore) sono coefficienti che si ricavano dalle tabelle.

Se si volesse trovare quanta potenza termica è necessaria per avere una portata di 4 , bisogna applicare la seguente formula:

(2.06)

Calcoli:

Dalla (2.03): 4,187 * (250 – 60) = 795

Dalla (2.04): 1713

Dalla (2.05): 2,1 * (300 – 250) = 105

Dalla (2.02): 795 + 1713 + 105 = 2614

Dalla (2.06): 4 * 2614 = 10456 10500 = 10500 KW.

Esercizio n° 3

Problema:

Si ha un contenitore, che si presume adiabatico, in esso sono contenuti 10 Kg di acqua e 1 Kg di vapore.

La pressione iniziale è pari a 1 bar, la pressione finale è di 5 bar.

Ovvero il contenitore è chiuso ed ermetico e non cambia volume, quindi praticamente rigido; viene somministrato una determinata quantità di calore Q tale che innalzi la pressione interna da 1 a 5 bar.

Scopo del problema:

Calcolare le condizioni finali e il calore che bisogna sommnistrare per far avvenire la trasformazione.

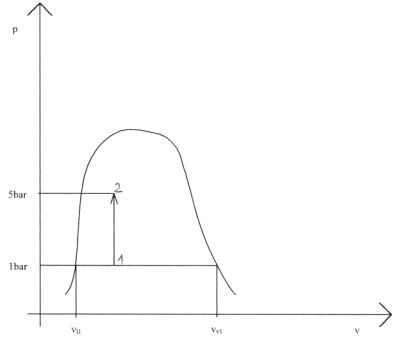
Figura 5 Diagramma (p-v) del vapore.

Risoluzione del problema:

Ci si riconduce sempre al diagramma (p-v). (Fig. 5)

In un Sistema chiuso rimangono invariati il volume, la massa, e la variazione di energia deriva solo dal calore somministrato dall’esterno.

Equazione sulla Conservazione della massa:

(3.01)

Dove l e v indicano la massa relativa al liquido e al vapore.

Equazione sulla Conservazione del volume:

(3.02)

Si riscriva la (3.02) in termini di volumi specifici e di massa:

(3.03)

Ma i seguenti prodottie possono essere trascurati.

Si mette a sistema la (3.01) e la (3.03) e si ricava che:

M_v2 = (3.04)

(3.05)

Dalle tabelle termodinamiche si ricava quanto vale il volume del liquido alla pressione di 1 bar e quanto vale il volume del vapore alla pressione di 5 bar.

Si conoscono le masse si conoscono anche i titoli x₁ e x₂ e valgono rispettivamente:

x₁ = (3.06)

x₂ = (3.07)

Il calore necessario per riscaldare il sistema vale:

(3.08)

(3.09)

Riprendendo l’equazione (1.07) si trova che:

u₂ = (3.10)

nello stesso modo si calcolo u_1.

Calcoli:

Dalla (3.04): M_v2 = = 4,5 Kg

Dalla (3.05): M_v1 = 10 + 1 – 4,5 = 6,5 Kg

Dalla (3.06): x₁ = = 0,09

Dalla (3.07): x₂ = = 0,41

Dalla (3.10): u₂ = = 1427

u₁ = = 607

Dalla (3.09): = 9020 KJ.

Esercizio n° 4

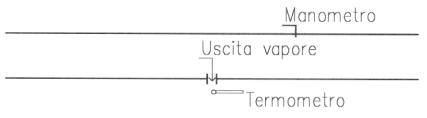
Figura 6

Problema:

Il sistema è costituito da una tubazione che è attraversata da vapore umido, il cui titolo non è noto. (Fig. 6)

All’interno del sistema si ha una pressione p pari a 39,7 bar, mentre la pressione ambientale è di 1 bar.

Scopo del problema:

Si vuol determinare il titolo del vapore contenuto nella tubazione.

Risoluzione del problema:

Si usa un metodo molto semplice, per il quale viene fatto uscire del vapore, da un piccolo foro nella tubazione. In questo punto viene posto un termometro che dovrà misurare la temperatura di uscita di questo vapore, questo servirà per conoscere il titolo x.

È un sistema aperto, ma la massa si conserva, perché non si verificano scambi di calore e di energia.

Si pensi ad una espansione adiabatica e si guardi il diagramma (p-v). (Fig. 7)

Equazione dell’Energia riferita al sistema aperto:

(4.01)

Non si verifica scambio di lavoro in quanto non c’è un dispositivo tecnico che dall’esterno scambia lavoro.

Quindi H₂ = H₁ e conservandosi la massa anche

h₂ = h₁ (4.02)

Dalle tabelle termodinamiche si ricava che ad una pressione di 39,7 bar la temperatura vale 250° C.

Nel punto 2₁ si avrà una temperatura di 100° C mentre nel punto 2, cioè all’uscita, si avrà una temperatura di 115° C.

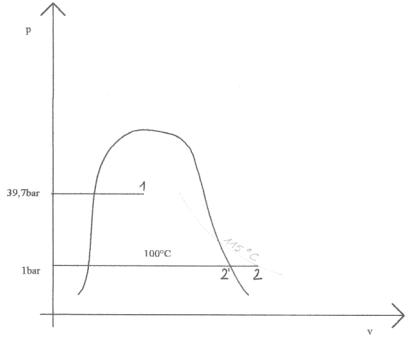
Figura 7 Diagramma (p-v) del vapore.

I corrispondenti valori dell’entalpia nei diversi punti sarà uguale a:

(4.03)

(4.04)

In questo caso x₂ vale 1 perché il vapore saturo è secco in quanto non è presente il liquido.

h_c2 indica il calore specifico del liquido.

Noto h₂ per la (4.02) si conosce anche h₁, quindi dalla (4.03) si ricava x₁ e vale:

x₁ = (4.05)

Calcoli:

Dalla (4.04): h₂ = 4,187 * 100 + 2257 + 1,95 * (115–100) = 2705

Dalla (4.05): x₁ = = 0,97.

Esercizio n° 5

Problema:

In un recipiente a pareti rigide è contenuto vapore umido alla pressione di 1e il titolo x = 0,644.

Scopo del problema:

Determinare la pressione necessaria per trasformare il vapore umido in vapore saturo secco, e qual è la quantità di calore che bisogna fornire per unità di massa per far avvenire tale trasformazione.

Risoluzione del problema:

Si considera sempre il diagramma (p-v). Trasformare il vapore umido in vapore secco significa che il punto 2 dovrà essere sulla curva limite superiore. (Fig. 8)

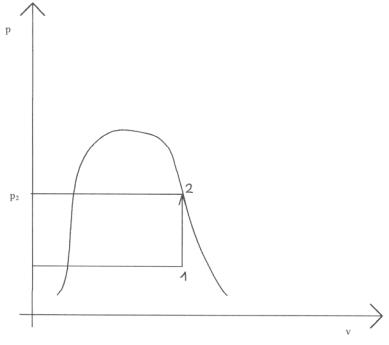
Figura 8 Diagramma (p-v) del vapore.

Il contenitore essendo rigido non altererà il suo volume e la massa quindi anche il volume specifico rimarrà invariato.

Poiché si è all’interno della curva di Andrews, nota la pressione nel punto 1 si conosce anche la temperatura in tal punto. Quindi t₁ = 99,1° C.

Visto che il volume e la massa sono costanti si può scrivere:

(5.01)

Di conseguenza: v₁ = v₂

Ma v₁ si può scrivere anche in altro modo, vedi la (1.03) v_i =

Una volta calcolato v₁ dalle tabelle si ricava p₂.

Il calore necessario sarà uguale a:

Δu = q = u₂ – u₁ (5.02)

Dalla (3.09) si ricavano u_2, u₁, con la seguente formula: u₂ =

Calcoli:

Dalla (1.03): v₁ = 0,001 + 0,644 * 1,724 = 1,12

Quindi p₂ = 1,569 bar

Dalla (3.09): u₂ = = 2436

u₁ = = 1745

Dalla (5.02): Δu = 2436 - 1745 = 671

Appendice

Vapore d’acqua saturo

t	p	vl	vv	ul	uv	hl	hv
°C	KPa	m^3/Kg	m^3/Kg	KJ/Kg	KJ/Kg	KJ/Kg	KJ/Kg
0.01	0.6113	0.001000	206.14	0.00	2375.3	0.01	2501.4
10	1.2276	0.001000	106.38	42.00	2389.2	42.01	2519.8
20	2.3390	0.001002	57.79	83.95	2402.9	83.96	2538.1
30	4.246	0.001004	32.89	125.78	2416.6	125.79	2556.3
40	7.384	0.001008	19.52	167.56	2430.1	167.57	2574.3
50	12.349	0.001012	12.03	209.32	2443.5	209.33	2592.1
60	19.940	0.001017	7.671	251.11	2456.6	251.13	2609.6
70	31.19	0.001023	5.042	292.95	2469.6	292.98	262.8
80	47.39	0.001029	3.407	334.86	2482.2	334.91	2643.7
90	70.14	0.001036	2.361	376.85	2494.5	376.92	2660.1

t	p	vl	vv	ul	uv	hl	hv
°C	MPa	m^3/Kg	m^3/Kg	KJ/Kg	KJ/Kg	KJ/Kg	KJ/Kg
100	0.10135	0.001044	1.6729	418.94	2506.5	419.04	2676.1
110	0.14327	0.001052	1.2102	461.14	2518.1	461.30	2691.5
120	0.19853	0.001060	0.8919	503.50	2529.3	503.71	2706.3
130	0.2701	0.001070	0.6685	546.02	2539.9	546.31	2720.5
140	0.3613	0.001080	0.508	588.74	2550.0	589.13	2733.9
150	0.4758	0.001091	0.39289	631.68	2559.5	632.20	2746.5
160	0.6178	0.001102	0.3071	674.87	2568.4	675.55	2758.1
170	0.7917	0.001114	0.2428	718.33	2576.5	719.21	2768.7
180	1.0021	0.001127	0.19405	762.09	2583.7	763.22	2778.4
190	1.2544	0.001141	0.15654	806.19	2590.0	807.62	2786.2
200	1.5538	0.001157	0.12736	850.65	2595.3	852.45	2793.2
210	1.9062	0.001173	0.10441	895.53	2599.5	897.76	2798.5
220	2.318	0.001190	0.08619	940.87	2602.4	943.62	2802.1
230	2.795	0.001209	0.07158	986.74	2603.9	990.12	2804.0
240	3.344	0.001229	0.05976	1033.21	2604.0	1037.32	2803.8
250	3.973	0.001251	0.05013	1080.39	2602..4	1085.36	2801.5
260	4.688	0.001276	0.04221	1128.39	2599.0	1134.37	2796.9
270	5.499	0.001302	0.03564	1177.36	2593.7	1184.51	2789.7
280	6.412	0.001332	0.03017	1227.46	2586.1	1236.0	2779.6
290	7.436	0.001366	0.02557	1278.92	2576.0	1289.1	2766.2
300	5.851	0.001404	0.02167	1332.0	2563.0	1344.0	2749.0
310	9.856	0.001447	0.018350	1387.1	2546.4	1401.3	2727.3
320	11.274	0.001499	0.015488	1444.6	2535.5	1461.5	2700.1

t	p	vl	vv	hl	hv	r
°C	bar	m^3/Kg	m^3/Kg	KJ/Kg	KJ/Kg	KJ/Kg
96	0.87686	0.001040	1.9153	402.2	2669.7	2267.5
98	0.94301	0.001042	1.7893	410.6	2672.9	2262.2
100	1.0135	0.001044	1.6729	418.94	2506.5	2256.9
102	1.0878	0.001045	1.5655	427.5	2679.1	2251.6
104	1.1668	0.001046	1.4662	435.9	2682.2	2246.3
106	1.2504	0.001048	1.3743	444.4	2685.3	2240.9
108	1.3390	0.001050	1.2889	452.9	2688.3	2235.4
148	4.5101	0.001088	0.41288	623.5	2743.0	2119.5
150	4.7600	0.001090	0.39245	632.1	2745.4	2113.2
152	5.0208	0.001093	0.37322	640.8	2747.7	2106.9
154	5.2929	0.001095	0.35510	649.4	2750.0	2100.6
156	5.5767	0.001097	0.33803	658.1	2752.3	2094.2
158	5.8725	0.001099	0.32194	666.8	2754.5	2087.7
160	6.1806	0.001102	0.30676	675.5	2756.7	2081.3
240.88	34			1041.3	2802.1	1760.3
244.16	36			1057.5	2801.7	1744.2
247.31	38			1072.7	2801.1	1728.4
250.33	40			1087.4	2800.3	1712.9
253.24	42			1101.5	2799.4	1697.8
256.05	44			1115.4	2798.3	1682.9
258.75	46			1128.8	2797.0	1668.3
261.37	48			1141.8	2795.7	1653.9