![]()
Il concetto di Entropia
Conosciamo lo stato termodinamico di un sistema se conosciamo i valori uniformi delle coordinate scelte per descriverlo. In particolare lo stato è di equilibrio se tali valori restano costanti nel tempo. Fra le variabili che descrivono un sistema termodinamico esiste sempre un legame che si chiama equazione di stato:
![]()
Le variabili sono in numero limitato, direttamente misurabili, non implicano ipotesi sulla struttura della materia e sono suggerite dai nostri sensi. Il loro numero e il tipo dipende dal tipo di sistema, se è semplice le grandezze indipendenti sono due: se ho un sistema composto da acqua e ne conosco pressione e volume, la temperatura è unica. Durante un passaggio di stato, in cui T è costante, ricavo p da v e viceversa.
Il passaggio dalla constatazione teorica del fatto che le grandezze termodinamiche siano legate fra loro alla definizione di equazioni che permettano di ricavarne i valori è piuttosto complesso, possiamo però avvalerci di tabelle da cui ricavare le coordinate termodinamiche p, v, T (grandezze primarie), entropia, entalpia, energia interna (grandezze secondarie ricavabili dalle precedenti). I valori delle grandezze secondarie dipendono solo dalle coordinate primarie di un certo stato di equilibrio, e non dal modo con cui tale stato è stato raggiunto, perciò si chiamano funzioni di stato.
La funzione di stato entropia (o "calore non utilizzabile") fu introdotta da Clausius nel 1865 per fornire una misura dell’utilizzo del calore come fonte di lavoro e trovare una risposta alla degradazione dell’energia e all’irreversibilità delle trasformazioni. Ma la definizione del concetto di entropia è elaborata, dipende dal ciclo di Carnot, è legata alla qualità di energia e si può spiegare come impedimento alla trasformazione di tutta l’energia contenuta in un sistema in lavoro. Non è possibile darne una definizione univoca, perché può essere presentato sotto vari aspetti con approcci diversi: l’entropia non è una grandezza direttamente misurabile, la sua esistenza non è direttamente suggerita dall'esperienza e non è percepibile dai sensi. Tuttavia è una grandezza fisica fondamentale per capire i fenomeni che avvengono in natura.
L’entropia è un modo per sapere se un determinato stato è raggiungibile da un sistema per mezzo di una trasformazione naturale e spontanea. Consideriamo due stati di un sistema isolato, A e B. Se l’entropia è maggiore nello stato B, questo può essere raggiunto spontaneamente dallo stato A. Viceversa lo stato A non può essere raggiunto dallo stato B senza rompere l’isolamento.
Un sistema isolato che compie una trasformazione spontanea irreversibile evolve sempre verso stati che implicano un aumento della sua entropia. Poiché l'Universo è un sistema isolato, ogni trasformazione in natura comporta un aumento complessivo dell'entropia nell'Universo. Il concetto di entropia afferma l’asimmetria della natura, (da A si può raggiungere B ma da B non si ritorna ad A) e costituisce l'enunciato più generale del II Principio della Termodinamica (o "principio dell’entropia"): Qualunque trasformazione spontanea è accompagnata da un aumento dell’entropia dell’universo.
In Fisica i Principi di conservazione sottolineano che una grandezza si mantiene costante. L’entropia è una grandezza anomala, in quanto per essa non vale invece un principio di creazione. L'aumento di entropia è un accrescimento vero e proprio.
Esempio
Se ho due serbatoi – uno di acqua calda e uno di acqua fredda – non posso utilizzare tutto il calore per ricavarne lavoro: ne andrà persa una parte come cascame termico. Possiamo riformulare il Secondo Principio, o principio dell’impossibilità, nell’enunciato di Calusius:
Non è possibile realizzare una trasformazione il cui unico risultato sia un trasferimento di calore da un corpo a temperatura inferiore a un corpo a temperatura superiore.
… oppure nell’enunciato di Kelvin:
In un processo ciclico, non è possibile convertire interamente calore in lavoro senza che avvenga una qualche variazione dell’ambiente.
Cioè non esiste una macchina termica ideale: il calore prodotto da una sorgente solo in parte si trasforma in lavoro, la restante parte sarà assorbita da un’altra sorgente, disperdendo in calore parte dell’energia spesa.
Attenzione!
La parte di energia "persa" non è effettivamente andata distrutta, infatti non posso contraddire il Primo Principio (Conservazione dell’energia), essa si è solo degradata in una forma non più utilizzabile per produrre lavoro.
Esempio
Un’automobile che frena trasforma il lavoro meccanico, attraverso l’attrito delle ruote sull’asfalto, in calore: è impossibile che il terreno e le ruote riscaldate mettano in moto l’auto! Questo esempio dà un’idea delle trasformazioni irreversibili.
Teorema: la freccia del tempo
Considerato l’universo uno scatolone adiabatico (isolato e chiuso in sé stesso, l’entropia totale dell’universo aumenta inevitabilmente.
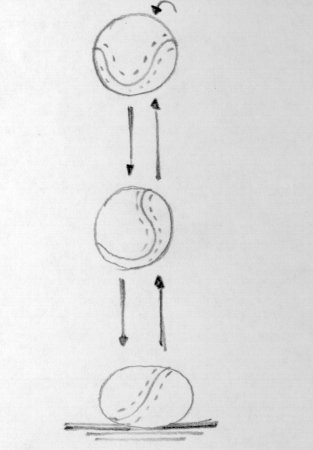
In natura sono teoricamente possibili trasformazioni reversibili, come l’urto perfettamente elastico di una palla che impatta sul pavimento e riprende a salire in un ciclo continuo di trasformazione dell’energia, ma in pratica gli attriti e le forze esterne impediscono che il movimento continui all’infinito.
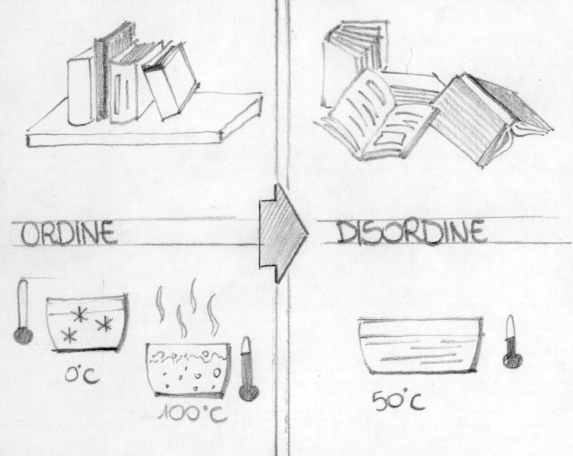
La freccia del tempo indica il verso in cui possono avvenire i fenomeni. Dal principio di aumento di entropia ricaviamo la nozione di "scorrere del tempo": l’evoluzione dell'Universo è una conseguenza dell'irreversibilità dei processi spontanei. Il fatto che un sistema isolato evolva spontaneamente verso maggiore entropia implica l'esistenza di una sequenza temporale degli eventi: la direzione dell’universo è portata al disordine, la vita stessa porta verso il disordine.
Definizione di Entropia assoluta
Considerato un sistema chiuso, la variazione di entropia del sistema è data dal calore fornito fratto la temperatura a cui è stato fornito
:![]()
Attenzione!
La temperatura è misurata nella scala assoluta: K = 273 + °C. Infatti T deve essere maggiore di zero, perché se T = 0, Q/T = Q/0 = entropia infinita.
Questa formula inoltre presuppone che il sistema mantenga temperatura costante durante il processo, il che non è vero in generale: T aumenta all’aumentare del calore fornito. Posso ragionare per assurdo su intervalli infinitesimi a T costante che approssimano la funzione: ciò equivale a ricorrere al concetto di integrale:
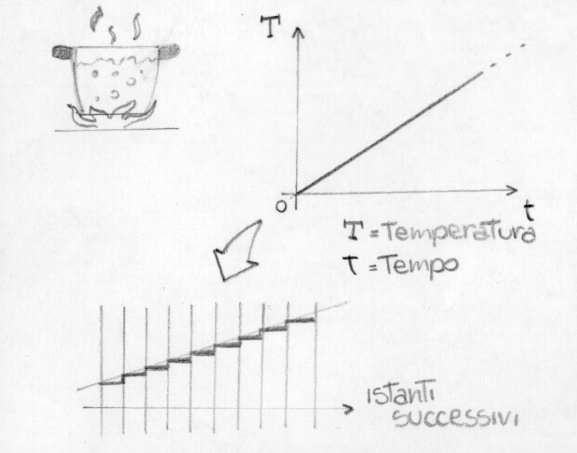
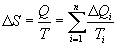
La variazione specifica di entropia è la variazione assoluta nell’unità di massa:
![]()
Il teorema di Clausius
Qual è il rapporto tra l’aumento di entropia e la diminuzione di exergia?
Teorema
In un processo irreversibile, un’exergia, pari al prodotto della variazione di entropia dell’universo per la temperatura del termostato più freddo disponibile, viene trasformata in modo da non essere più in grado di compiere lavoro.
![]()
Lavoro perduto = exergia perduta = temperatura del serbatoio più freddo X variazione di entropia del sistema adiabatico considerato.
La disponibilità di lavoro è inversamente proporzionale all’entropia: maggiore è l’exergia di un sistema, minore è la sua entropia. La variazione di entropia consente di misurare quanta energia utilizzabile come lavoro è ricavabile all’interno di un processo termodinamico e quanto lavoro è stato perduto. È un indice del grado di degradazione dell’energia: l’energia a bassa entropia è energia pregiata, ad alto contenuto exergetico, con buona convertibilità. L’entropia identifica il modo in cui l’energia si trova immagazzinata, se è ad alta temperatura la sua entropia è bassa e la sua qualità e alta, se è a bassa temperatura l’entropia è alta e la qualità è bassa. L’aumento di entropia del sistema è indicatore di una trasformazione spontanea nella quale l’energia viene immagazzinata a temperature più basse: la direzione spontanea di una trasformazione produce una diminuzione della qualità dell’energia.
Esercizio: Irreversibilità di una trasformazione
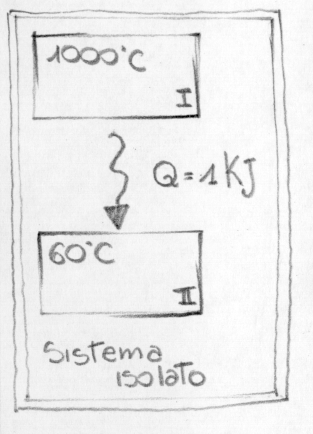
Il sistema è composto da due serbatoi assimilabili a pozzi di calore. Una quantità di calore Q=1KJ è ceduta dal serbatoio a 1000°C a quello a 60°C. Di quanto è variata l’entropia del sistema composto dai due serbatoi?
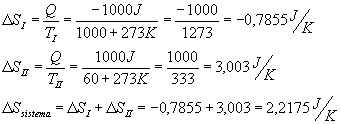
Osservazione
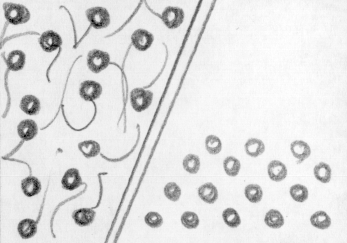
Ad uno stato termodinamico a temperatura maggiore corrisponde un’entropia maggiore: sottraendo calore, l’entropia diminuisce. Ad uno stato termodinamico a temperatura minore corrisponde un’entropia minore: fornendo calore, l’entropia aumenta. Complessivamente, il sistema ha aumentato la sua entropia: è confermata la legge dell’aumento inesorabile dell’entropia dell’universo.
Il passaggio di calore tra due corpi a temperature diverse determina una trasformazione irreversibile: non può avvenire il contrario senza compiere lavoro sul sistema. In questo caso abbiamo che:
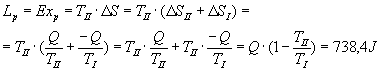
dove Lp è il lavoro che non può più essere ricavato dal sistema a causa dell’uniformarsi della sua temperatura.
L’entropia nella trasformazioni
Essendo l’entropia una funzione di stato, se conosco le grandezze relative ad un certo stato termodinamico posso ricavarla immediatamente. In particolare, non dipende dal tipo di trasformazione o dal suo percorso: ma è sempre data dalla differenza tra i valori di entropia negli stati iniziale e finale. Essa dipende però dalle irreversibilità interne al sistema. Vediamo il comportamento di questa grandezza nell’ambito delle trasformazioni fisiche più "facili":
Attenzione!
Nelle trasformazioni adiabatiche,
![]()
è necessario tenere conto delle trasformazioni interne al sistema.
![]()
A livello teorico, se abbiamo un sistema adiabatico senza irreversibilità interne (si è verificata una trasformazione completamente reversibile), la variazione di entropia del sistema è nulla. Infatti le trasformazioni adiabatiche sono chiamate anche isoentropiche.
Trasformazioni isoterme - diagramma dei gas ideali
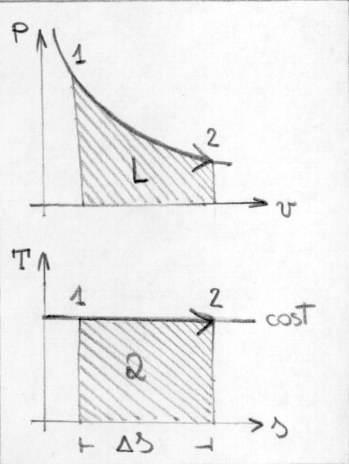
Curva caratteristica: iperbole equilatera
![]()
lavoro = area sottesa
Q = area sottesa
![]()
Si vedono i trasferimenti di calore
Trasformazioni adiabatiche - diagramma dei gas ideali
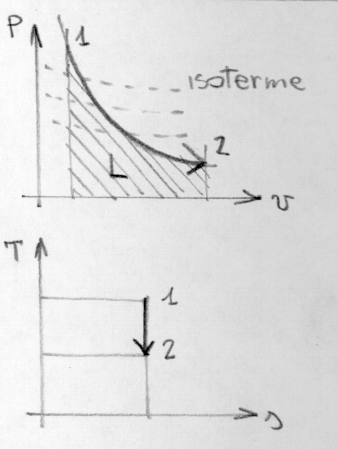
Curva caratteristica:
![]()
L = area sottesa
Q = 0: non c’è variazione di entropia, sempre solo se le trasformazioni sono reversibili, ma la variazione di entropia interna è solitamente di difficile definizione.
Il diagramma PVT dell’acqua
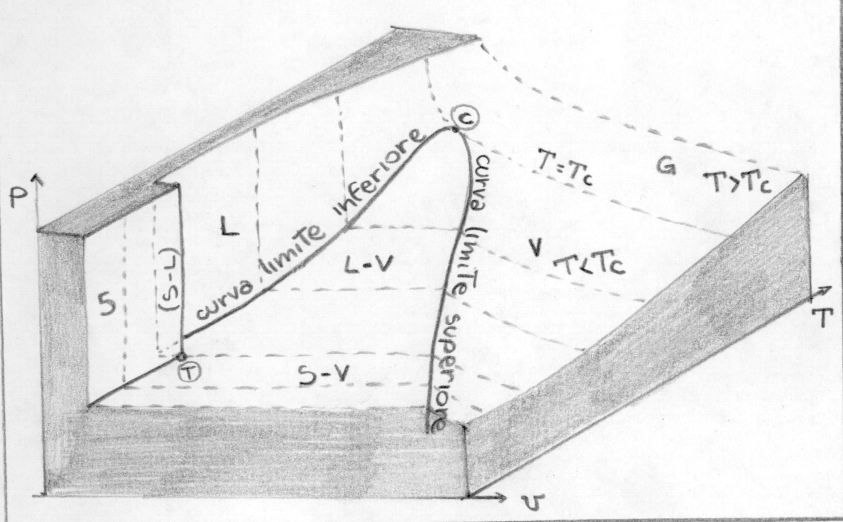
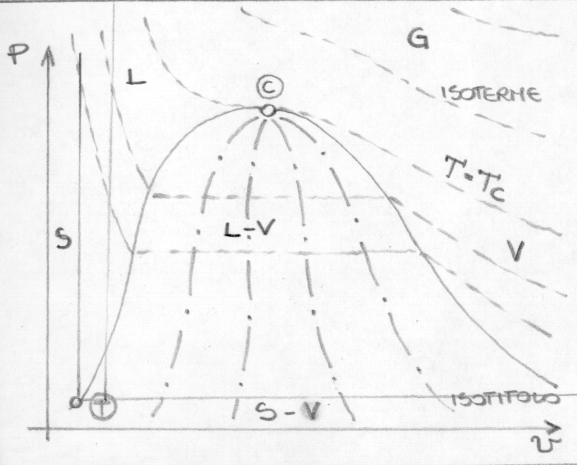
Definito un sistema tridimensionale di assi cartesiani a cui assegnare i valori di p, v, T, ad ogni terna (ottenuta sperimentalmente) corrisponde un punto della superficie che descrive gli stati di equilibrio dell’acqua. Per questioni di praticità riduciamo la rappresentazione in due dimensioni, recuperando l’indicazione della temperatura dalle isoterme. Calcoliamo quindi le proprietà termodinamiche dell’acqua (volume specifico -v- , entropia -s-, entalpia -h-, energia interna -u-) nelle varie zone del diagramma, noti p, v, T. Ricorda che il diagramma dà informazioni sugli stati di equilibrio ma non descrive il processo di trasformazione (che non conserva l’equilibrio in caso di trasformazioni rapide).
Liquido sottoraffreddato
Ci troviamo nella zona compresa tra l’isoterma critica e la curva limite inferiore. Sappiamo che
![]()
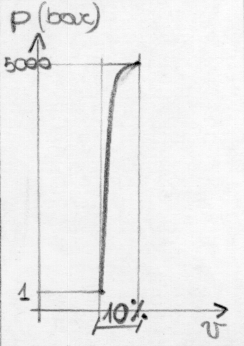
cioè il volume specifico varia in funzione della temperatura. In realtà i liquidi non sono incomprimibili, infatti il volume dipende anche dalla pressione, perché diminuisce leggermente (10% ca.) aumentando p. Ma per il campo di azione che ci interessa la variazione è talmente piccola da non essere presa in considerazione.
Una caratteristica più interessante, perché anomala, dell’acqua è la variazione della densità in rapporto alla temperatura:
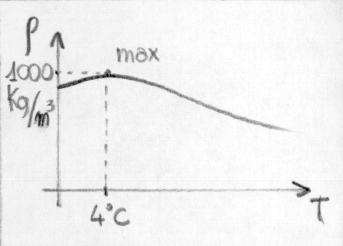
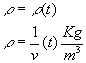
Il picco massimo si ha ad una densità di 4°C (definizione di laboratorio). Grazie a questa caratteristica, in prossimità del congelamento si ha che l’acqua più calda sta sul fondo, mentre gela solo in superficie: ciò ha permesso la vita nei mari ed è origine dei moti convettivi, degli iceberg ecc.
|
t - Temperatura in gradi Celsius |
r - Densità in Kg/m3 |
|
0°C |
999,84 |
|
4°C |
1000 |
|
10°C |
999,70 |
|
20°C |
998,21 |
|
30°C |
995,65 |
|
40°C |
992,22 |
|
50°C |
988,04 |
|
60°C |
983,20 |
|
70°C |
|
|
80°C |
971,79 |
Andamento del calore specifico ed energia interna
Cp = calore specifico in funzione della pressione
Cv = calore specifico in funzione del volume
Il calore specifico non varia in funzione della trasformazione, ma dipende solo dalla temperatura. Visto che l’acqua non varia di molto il suo volume specifico al variare della pressione, possiamo operare la semplificazione:
![]()
Dall’enunciato del secondo principio della termodinamica abbiamo che:
![]()
In questo caso, essendo la variazione minima, il lavoro L compiuto è trascurabile. Perciò la variazione di energia interna è uguale al calore fornito:
![]()
Per convenzione, l’energia interna alla temperatura di 0°C è
![]()
Per la definizione di calore specifico,
![]()
Perciò il calore specifico è fondamentale per il calcolo dell’energia interna:
![]()
|
t - Temperatura in gradi Celsius |
Cl – calore specifico in J/KgK |
|
0°C |
4217 |
|
20°C |
4187 |
|
80°C |
4196 |
Esercizio
Abbiamo un sistema chiuso omogeneo composto da 1 kg di acqua scaldato da T1 a T2. Qual è la variazione di energia interna del sistema riconducibile al calore scambiato?
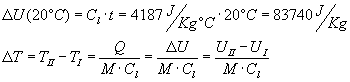
L’entalpia specifica
![]()
Di solito, (p v) vale molto poco:
![]()
perciò posso considerare questo termine trascurabile. Quindi in prima approssimazione l’entalpia è equivalente all’energia interna:
![]()
Attenzione!
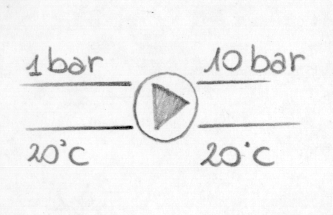
Ciò non vale nel caso in cui abbiamo una pompa che compie lavoro su un fluido in un sistema aperto, infatti l’equazione risulta:
![]()
trascurando il prodotto p v, abbiamo ignorato il lavoro compiuto dalla pompa: contraddicendo il principio della conservazione dell’energia: la pompa ha speso lavoro ma l’entalpia non è incrementata, non è cambiata l’energia interna del sistema. Scriviamo in termini estesi:
![]()
dove L = lavoro compiuto dalla pompa. Per il sistema aperto,
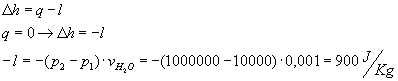
Quando abbiamo a che fare con pompe che agiscono sul fluido, il termine (p v) non è trascurabile.
La variazione di entropia
Formula per calcolare la variazione di entropia specifica di un sistema composto da acqua:
![]()
è la variazione di entropia da uno stato all’altro. Se fornisco calore, il suo incremento è direttamente proporzionale all’aumento di temperatura:
![]()
perciò:
![]()
Ma come prendere T al numeratore, dato che non è costante? Formula generale:
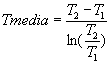
In particolare, per variazioni piccole, posso prendere la media aritmetica:
![]()
Esercizio
Essendo una funzione di stato, posso calcolare quanto vale l’entropia dell’acqua ad una certa temperatura, ad esempio 20°C (attenzione ad usare i Kelvin):
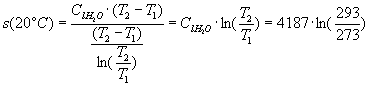
Ecco l’espressione generale con la quale posso calcolare il valore dell’entropia dell’acqua in funzione della temperatura:
![]()
Considerando un liquido, la funzione di stato dell’entropia in funzione di p e T si può calcolare abbastanza semplicemente. In particolare è possibile assegnare valore nullo all’entropia, in corrispondenza di uno stato di riferimento, scelto in modo da semplificare i calcoli, per esempio S=0 a 0°C. Il terzo principio della termodinamica precisa il valore assoluto dell’entropia: l’entropia di una sostanza pura omogenea è nulla quando la sostanza si trova alla temperatura dello zero assoluto.
Il procedimento si semplifica ulteriormente se consideriamo il passaggio di stato, durante il quale la temperatura è costante: vediamo la vaporizzazione.
Vapore saturo
È la porzione del diagramma PVT che si trova sotto la campana o "Curva di Andrews", si ha coesistenza di liquido e gas. Isoterme ed isobare coincidono ed i cambiamenti di stato avvengono in modo graduale.
Ricorda
Per titolo X si intende il rapporto fra la massa del vapore e la massa totale liquido + vapore:
![]()
A partire dalla formula per il volume specifico, ricaviamo in maniera analoga anche le altre:
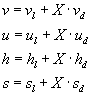
Sapendo che il volume differenziale è ottenuto sottraendo il volume del liquido al volume del vapore:
![]()
In particolare l’entropia differenziale non viene tabulata, mentre l’entalpia differenziale corrisponde al calore latente di vaporizzazione:
![]()
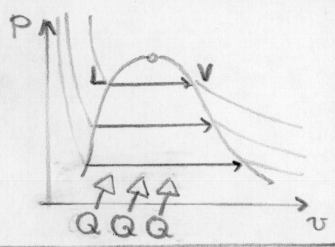
Riprendiamo lo studio della campana: la trasformazione che porta da un qualsiasi punto ad un altro interni alla campana è visualizzabile come una retta orizzontale che congiunge L - liquido e V - vapore. Per passare a L a V ho bisogno di fornire al sistema una quantità di calore pari al calore latente di vaporizzazione
![]()
Quant’è la variazione di entropia (sd) nel passaggio completo da L a V? Essa è pari nel suo incremento al calore fornito fratto la temperatura costante. Il calore ricevuto dall’acqua durante tutto il passaggio da L a V è pari al calore latente di vaporizzazione.
![]()
Vapore surriscaldato
È la porzione di grafico PVT che si trova tra la curva limite superiore e l’isoterma critica, il vapore è isotermicamente trasformabile in liquido per compressione. Procediamo con una trasformazione isobara, per esempio alla pressione atmosferica.
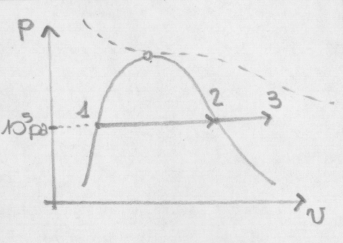
Consideriamo nel grafico i punti 2 e 3, di cui il primo sulla curva limite e il secondo nella zona dei vapori surriscaldati: il punto 2 è alla medesima pressione del punto 3 ma a temperatura più bassa. Le proprietà del punto 3 si legano a quelle del punto 2, di cui sono note pressione e temperatura. Scriviamo le proprietà del vapore in analogia con le proprietà dei gas ideali (p v costante in funzione di T).
![]()
Formule
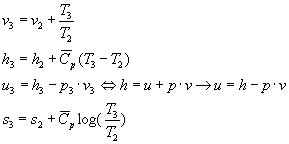
L’unico problema è che per i gas Cp varia in funzione della temperatura, dobbiamo allora usare il Cp medio (lineetta sopra).
Gas perfetti
Quando la temperatura supera di due volte la temperatura critica Tc, ci troviamo molto lontano dalla campana: possiamo usare le equazioni dei gas perfetti. Le isoterme tendono ad assumere un andamento di iperboli equilatere, il gas non può più essere trasformato in liquido.
Formule
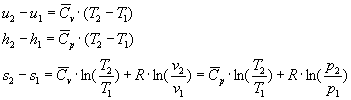
dove R è la costante dei gas perfetti, cioè secondo la l’equazione di stato dei gas perfetti:
![]()
Approfondimento: entropia e probabilità
Il concetto di entropia aiuta a comprendere la direzione in cui evolvono i sistemi termodinamici. Il II Principio pone ulteriori limitazioni ai processi naturali, oltre a quelle che derivano dal I Principio: infatti l’esperienza comune indica molti fenomeni che non avvengono in Natura pur non contraddicendo il Primo Principio. Per fare solo un esempio: un gas libero di espandersi tende ad occupare tutto il volume accessibile. La conservazione dell’energia non vieterebbe che il gas, inizialmente distribuito, spontaneamente occupasse solo una frazione del volume.
Un sistema complesso isolato lasciato a se stesso tende ad evolvere dall'ordine verso il disordine. Poiché spontaneamente non avviene praticamente mai il contrario, possiamo definire questo passaggio come un processo irreversibile. Enunciamo il II Principio: ogni sistema isolato evolve verso stati di disordine crescente.
L’aumento di entropia è una misura del disordine del sistema: uno stato con poco disordine è quello nel quale i costituenti sono stati ordinati, uno stato ad alto disordine è quello in cui il sistema è disposto a caso. L’aumento dell’entropia di un sistema nelle trasformazioni reali equivale all’aumento del livello di disordine del sistema. I processi naturali tendono a rendere l’universo più disordinato.
|
Energia |
Entropia (J/K) |
|
|
|
Cinetica, potenziale gravitazionale e elettrica |
0 |
|
Termica, reazioni nucleari |
1011 |
|
Termica, entro il Sole |
107 |
|
Luce solare |
105 |
|
Termica, reazioni chimiche |
104 |
|
Termica, sulla Terra |
3 103 |
|
Termica, radiazione di fondo |
3 101 |
|
|
La tabella valuta la variazione di entropia che si ha nella conversione da una forma di energia ad un’altra. Quando la conversione avviene da forme più ordinate a più disordinate, si ottiene un aumento di entropia dell’Universo. Si avrebbe invece una diminuzione di entropia con processi opposti: per il Secondo Principio, ciò comporta che una parte di energia debba convertirsi in forme ancora più degradate con produzione complessiva di entropia positiva.
La Legge di Boltzmann
Boltzmann nel 1877 sottolineò la connessione tra la seconda legge e la teoria della probabilità: lo stato macroscopico verso cui evolve spontaneamente un sistema è quello che corrisponde al maggior numero di stati microscopici, cioè il più probabile. La grandezza microscopica associata all’entropia è la probabilità dei diversi modi di ordinare le molecole di un sistema. Essa porta spontaneamente verso lo stato di equilibrio in cui le molecole sono disposte nel modo più probabile possibile. Boltzmann ha sviluppato l’interpretazione probabilistica dell’entropia, e ha ricavato l’espressione statistica S = k log W (S = entropia, k = costante moltiplicativa, W = numero di configurazioni microscopiche corrispondenti allo stato macroscopico considerato).
Per misurare il disordine di un sistema dobbiamo conoscere il numero delle possibili posizioni in cui si possono trovare le sue particelle. La seconda legge della termodinamica afferma la prevalenza del passaggio spontaneo da stati meno probabili a stati più probabili, da meno a più confusi, da più ordinati a più disordinati, fino a raggiungere la distribuzione di equilibrio. ![]() Per questo un gas lasciato libero da vincoli si espande: esso tende a raggiungere uno stato di equilibrio termodinamico.
Per questo un gas lasciato libero da vincoli si espande: esso tende a raggiungere uno stato di equilibrio termodinamico.
Ogni volta che avviene una trasformazione spontanea, l’Universo si porta in uno stato più probabile. L’entropia raggiunge il massimo quando il sistema possiede il massimo numero di posizioni possibili per le sue particelle, uniformemente distribuite entro l’universo, cioè all’equilibrio termico. Esso rappresenta la morte di un sistema: esso cessa di trasformarsi, di evolversi, è impossibile ricavarne lavoro.
Trasformazioni spontanee e la freccia del tempo
È ragionevole pensare che la condizione di equilibrio, una volta dispersa uniformemente entro tutto l’universo, si raggruppi nuovamente? C'è la possibilità teorica che ciò avvenga, ma la probabilità risulta molto bassa, tanto da considerarsi trascurabile. La diffusione della condizione di equilibrio è spontanea, ma non si può spontaneamente ritornare indietro. È impossibile invertire i processi spontanei: come pensare che si ritorni da un disordine completo ad una condizione particolare?
Il secondo principio della termodinamica afferma che l’entropia di un sistema isolato aumenta sempre, che il flusso di energia si degrada continuamente, determinando la freccia termodinamica. In apparente contraddizione con ciò, l'esperienza offre esempi di sistemi che evolvono verso stati di ordine maggiore: uno degli aspetti degli organismi viventi è quello di eseguire reazioni che sembrano produrre una diminuzione di entropia. Nei sistemi complessi si generano organizzazioni, si crea ordine. In realtà il principio non è violato: si tratta di sistemi locali (in non-equilibrio) che ricevono da una fonte esterna (il Sole ad esempio) l’energia necessaria ad organizzarsi dissipandola nel fare ciò. Ogni volta che un sistema evolve verso stati di ordine maggiore, significa che non è isolato. Il maggior ordine raggiunto dal sistema è a scapito di maggior disordine riversato nell'ambiente: la diminuzione di entropia del sistema è compensata dall'aumento di entropia dell’ambiente. Localmente l'entropia può anche diminuire, ma complessivamente aumenta. L’Universo tende a raffreddarsi a causa dell’espansione, infatti la radiazione di fondo che si trovava 0.1 secondi dopo il Big Bang, alla temperatura di 100 miliardi K, ora è a 2.75 K. Le galassie cedono calore al fondo cosmico senza mai raggiungere l’equilibrio termodinamico. È lo scambio di calore delle galassie con l’Universo che genera entropia, ne consegue che la direzione temporale in cui l’entropia aumenta coincide con l’Universo che si espande (freccia cosmologica).
Ridurre l’entropia di un sistema
Per ridurre l’entropia di un sistema occorre intervenire su di esso fornendo energia proveniente da un ambiente esterno che alla fine paga il proprio intervento in termini di aumento della propria entropia. Ad esempio le piante trasformano costantemente elementi chimici prelevati dal terreno e dall’atmosfera in proteine vegetali, con processi che portano dal disordine verso l’ordine ai quali corrisponde una diminuzione di entropia. Il metabolismo vegetale richiede però la luce, senza la quale le piante non possono vivere: l’energia luminosa è il flusso che serve a ridurre l’entropia della pianta.
Glossario
Calore o energia termica
– energia interna che si trasmette da un corpo ad un altro unicamente in conseguenza di una differenza di temperatura. Fluisce spontaneamente da un corpo più caldo ad un corpo più freddo. Si misura in J come l’energia, deriva dal Principio Zero della Termodinamica.Calore specifico –
quantità di energia necessaria per dar aumentare di un grado (°C o K) l’unità di massa (1 Kg) di sostanza. L’acqua liquida ha un calore specifico molto elevato (4186 J/KgK), superiore a quello del ghiaccio (2060 J/KgK) o del vapore (2020 J/KgK).Calore latente
– di fusione, è il calore necessario per passare da S a L. Per l’acqua è pari a 3,34 105 J/Kg. Di vaporizzazione, è il calore necessario per passare da L a V. Per l’acqua è pari a 2,26 106 J/Kg ed è pari all’entalpia specifica differenziale. Durante la fusione e l’evaporazione è necessario fornire calore al sistema per spezzare i legami chimici delle particelle senza che aumenti l’agitazione termica, ovvero, a livello macroscopico, la temperatura del sistema.Ciclo di Carnot –
consiste in un ciclo ideale di quattro trasformazioni reversibili, due isotermiche e due adiabatiche, che permettono di calcolare il rendimento massimo di un motore. Esso non dipende dalla sostanza che compie il ciclo, ma solo dalla differenza di temperatura tra i due serbatoi tra cui opera ed è sempre inferiore al 100%. Nessuna macchina reale può avere un rendimento superiore a quello di una macchina di Carnot che lavori tra due serbatoi: è stabilito un limite superiore al rendimento dei motori reali. Una parte del calore prelevato dal primo serbatoio non può essere trasformata in lavoro e viene resa al secondo serbatoio. Si provoca un aumento dell’entropia del sistema, coerentemente con il II Principio della Termodinamica (enunciato di Kelvin), che afferma che non tutto il calore assorbito dalla macchina in un ciclo può essere convertito in lavoro, ma che necessariamente una certa parte deve essere ceduta ad altri corpi.Degradazione dell’energia
– l’energia di un sistema isolato si mantiene costante, ma può essere degradata. L’energia è tanto più preziosa quanto maggiore è il lavoro che se ne può ricavare: non tutte le forme di energia sono equivalenti: ci sono energie nobili e versatili (energia cinetica, potenziale, elettrica e chimica) che possono essere tramutate in lavoro quasi integralmente, e forme meno pregiate che possono essere trasformate solo con precise limitazioni. Il tipo di energia meno nobile è il calore, tanto meno pregiato quanto più bassa è la temperatura della sorgente da cui è estratto. Alla fine di ogni processo naturale c'è sempre una quantità di energia pregiata trasformata in forma meno pregiata. Chiamiamo energia degradata la quantità di energia che dopo una trasformazione irreversibile non può più essere utilizzata per compiere lavoro. L'energia divenuta inutilizzabile è proporzionale alla variazione totale di entropia prodottasi a causa dell'irreversibilità del processo.Energia interna
– somma dell’energia cinetica e dell’energia potenziale possedute da un corpo, chiamata anche energia di agitazione termica, che in corrispondenza dello zero assoluto è nulla. In un sistema isolato, si conserva sempre (Primo Principio della Termodinamica).Exergia –
Grandezza fisica definita come il massimo lavoro ricavabile da un sistema quando questo scambia energia con l’esterno. Più semplicemente, energia convertibile in lavoro. È legata al rendimento di Carnot e alla dispersione termica.Il secondo principio della termodinamica
– formulato da Clausius, può essere enunciato in vari modi equivalenti. Definisce le trasformazioni che, pur non essendo in contraddizione con il primo principio, non possono realmente avvenire. Il secondo principio si occupa della direzione naturale in cui si verifica il cambiamento di distribuzione dell'energia, dà un verso preferenziale alla "freccia del tempo" perché stabilisce che i sistemi evolvono in una direzione temporale, ma non nell’altra. Sebbene la quantità totale dell'energia debba conservarsi in qualunque processo, la distribuzione dell'energia cambia in modo irreversibile. Ciò porta all’introduzione del concetto di entropia. Riformuliamo il secondo principio in termini di entropia: "in qualsiasi trasformazione termodinamica che evolva tra due stati di equilibrio, l’entropia del sistema costituito dal sistema più l’ambiente circostante può solo restare costante o aumentare."Le trasformazioni termodinamiche
– sono i processi attraverso cui i sistemi passano da uno stato termodinamico ad un altro. Se lo stato finale coincide con lo stato iniziale, la trasformazione si dice ciclica. Le trasformazioni termodinamiche sono caratterizzate dal modo di evolversi del sistema, quelle più comuni sono le isoterme (temperatura costante), le isobare (pressione costante), le isocore (volume costante), le adiabatiche (il sistema non scambia calore con l'ambiente).
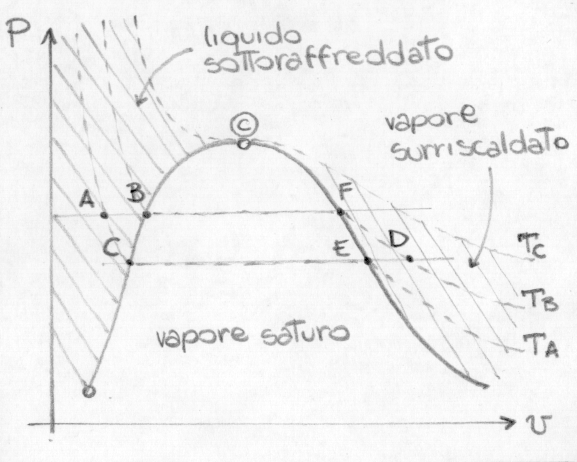
Liquido sottoraffreddato e vapore surriscaldato
– i termini non si riferiscono al valore assoluto della temperatura. È sottoraffreddato il liquido in A perché si trova a temperatura inferiore di quella del liquido saturo in B alla stessa pressione, oppure perché si trova a pressione superiore rispetto al liquido saturo in C che ha la stessa temperatura. È surriscaldato il vapore in D perché si trova a temperatura superiore di quella del vapore saturo in E alla stessa pressione, oppure perché si trova a pressione inferiore rispetto al vapore saturo in F che ha la stessa temperatura.Pozzi, serbatoi o Sorgenti di calore
– Esistono sistemi di massa e capacità termica così elevate, che possono scambiare quantità illimitate di calore mantenendo costante la temperatura. In natura non esistono sorgenti di calore, ma con buona approssimazione possiamo considerare tale l'acqua del mare. Nella pratica questa caratteristica è facilmente ottenibile portando il sistema nella fase di cambiamento di stato. In questo modo T è costante, perciò non serve integrare.Sistema universo
- Tra i sistemi isolati, quelli cioè che non possono scambiare né materia né energia con i corpi che li circondano, indicati come "ambiente circostante", chiamiamo Universo l'insieme del sistema e del suo ambiente, intendendo tutto ciò che ha interagito, più o meno direttamente, con il sistema stesso. l'Universo è sempre un sistema isolato, altrimenti dovremmo ammettere un altro sistema ed esso esterno.Titolo
– numero puro che può variare nell’intervallo di valori [0,1]. Indica, per ogni punto della campana, in che proporzione sono presenti la fase liquida e gassosa e quindi quali sono le proprietà della sostanza nel punto. Infatti le proprietà dei vapori saturi corrispondono alla somma pesata delle proprietà dei componenti.X=0 à non esiste vapore: liquido saturo à curva limite inferiore
X=0à non esiste liquido: vapore saturo secco à curva limite superiore
Trasformazioni reversibili e irreversibili –
sono reversibili le trasformazioni che avvengono in un tempo al limite infinito, in cui non sono presenti effetti dissipativi. Non esistono in natura, ma potremo con buona approssimazione considerare tali quelle in cui le coordinate termodinamiche cambiano molto lentamente e in cui sono stati ridotti al massimo gli attriti. Una trasformazione reversibile si svolge in modo tale che sia il sistema che l'ambiente circostante possono sempre essere riportati nello stato iniziale senza che nell'Universo resti traccia. Tutto ciò che avviene in un senso durante una trasformazione reversibile, accade nel senso opposto se si cambia il verso di percorrenza, ma non cambia il valore assoluto degli scambi energetici. Sono perfettamente reversibili i processi durante i quali la variazione di entropia totale (sistema + ambiente esterno) risulta nulla. La variazione di entropia tra due stati è definita da una trasformazione reversibile: se abbiamo a che fare con una trasformazione irreversibile (reale), dobbiamo considerare una qualunque trasformazione reversibile che collega i due stati: il risultato non cambia.Sono irreversibili le trasformazioni che avvengono in un tempo finito e/o nelle quali sono presenti effetti dissipativi. Una trasformazione irreversibile non è caratterizzata dal fatto che il sistema non possa essere ricondotto nello stato iniziale, ma dal fatto che ciò non possa avvenire senza che nell'ambiente circostante ne rimanga traccia. E’ possibile riportare il sistema allo stato iniziale, riducendone l’entropia, ma questa operazione è effettuabile a patto di compiere lavoro. Tutte le trasformazioni che avvengono in natura sono più o meno irreversibili. I processi in cui l'entropia aumenta sono irreversibili. Più alto è il grado di irreversibilità della trasformazione, maggiore è la variazione totale di entropia, e viceversa. L’irreversibilità è determinata dal numero di "gradi di libertà" delle particelle del sistema che si sta analizzando, cioè le possibili combinazioni di posizione e velocità in cui si possono trovare le particelle. Questo numero aumenta all’aumentare del numero di particelle prese in considerazione. E più sono i gradi di libertà, maggiore è la probabilità che un processo spontaneo sia irreversibile. Aumentando il numero di particelle, aumenta il disordine, e quindi l’irreversibilità di un determinato stato.
Appendice
Caratteristiche del vapore d’acqua saturo (dal punto triplo al punto critico).
|
T (°C) |
P (Mpa) |
v (m3/kg) |
vv |
u (kJ/kg) |
Uv |
h (kJ/kg) |
hv |
s (kJ/kgK) |
sv |
|
0,01 |
6,11 × 10-4 |
206,2 |
206,2 |
Zero |
2375,6 |
2501,6 |
2501,6 |
Zero |
9,157 |
|
20 |
2,34 × 10-3 |
57,8 |
57,8 |
83,9 |
2403,0 |
2454,3 |
2538,2 |
0,296 |
8,668 |
|
40 |
7,38 × 10-3 |
19,6 |
19,6 |
167,4 |
2430,2 |
2406,9 |
2574,4 |
0,572 |
8,258 |
|
60,1 |
0,02 |
7,65 |
7,65 |
251,4 |
2456,9 |
2358,4 |
2609,9 |
0,832 |
7,909 |
|
81,3 |
0,05 |
3,24 |
3,24 |
340,5 |
2484,0 |
2305,4 |
2646,0 |
1,091 |
7,595 |
|
100 |
0,101322 |
1,672 |
1,673 |
419,0 |
2506,5 |
2256,9 |
2676,0 |
1,307 |
7,355 |
|
151,8 |
0,50 |
0,374 |
0,375 |
639,6 |
2560,2 |
2107,4 |
2747,5 |
1,860 |
6,819 |
|
201,4 |
1,60 |
0,1225 |
0,1237 |
856,7 |
2593,8 |
1933,2 |
2791,7 |
2,344 |
6,418 |
|
250,3 |
4,00 |
0,0485 |
0,0497 |
1082,4 |
2601,3 |
1712,9 |
2800,3 |
2,797 |
6,069 |
|
300,1 |
8,60 |
0,0202 |
0,0216 |
1333,3 |
2564,9 |
1404,5 |
2750,9 |
3,256 |
5,708 |
|
349,8 |
16,50 |
0,0070 |
0,00883 |
1641,8 |
2423,1 |
898,3 |
2568,8 |
3,778 |
5,220 |
|
374,15 |
22,12 |
Zero |
0,00317 |
2308 |
2308 |
Zero |
2108 |
4,444 |
4,444 |
Caratteristiche del vapore d’acqua surriscaldato:
|
P (bar) |
1,2 |
1,4 |
1,6 |
|||||||
|
t (°C) |
T (K) |
H |
S |
V |
H |
S |
V |
H |
S |
V |
|
120 |
393,15 |
2714,4 |
7,3787 |
1490,1 |
2712,3 |
7,3033 |
1274,0 |
2710,1 |
7,2373 |
1111,9 |
|
140 |
413,15 |
2754,7 |
7,4788 |
1570,8 |
2753,0 |
7,4044 |
1343,7 |
2751,3 |
7,3395 |
1173,4 |
|
160 |
433,15 |
2794,8 |
7,5734 |
1650,5 |
2793,4 |
7,4998 |
1412,5 |
2792,0 |
7,4356 |
1234,0 |
|
180 |
453,15 |
2834,6 |
7,6634 |
1729,7 |
2833,5 |
7,5903 |
1480,7 |
2832,3 |
7,5266 |
1293,9 |
|
200 |
473,15 |
2874,4 |
7,7492 |
1808,4 |
2873,4 |
7,6765 |
1548,4 |
2872,5 |
7,6133 |
1353,4 |
|
220 |
493,15 |
2914,1 |
7,8315 |
1886,7 |
2913,3 |
7,7591 |
1615,7 |
2912,5 |
7,6962 |
1412,5 |
|
240 |
513,15 |
2953,9 |
7,9106 |
1964,7 |
2953,2 |
7,8384 |
1682,8 |
2952,5 |
7,7758 |
1471,3 |
|
260 |
533,15 |
2993,8 |
7,9869 |
2042,6 |
2993,2 |
7,9149 |
1749,7 |
2992,6 |
7,8524 |
1530,0 |
|
280 |
553,15 |
3033,8 |
8,0605 |
2120,3 |
3033,3 |
7,9887 |
1816,4 |
3032,7 |
7,9263 |
1588,5 |
|
300 |
573,15 |
3074,0 |
8,1319 |
2197,9 |
3073,5 |
8,0601 |
1883,0 |
3073,0 |
7,9979 |
1646,8 |
|
350 |
623,15 |
3175,3 |
8,3012 |
2391,5 |
3174,4 |
8,2297 |
2049,1 |
3174,5 |
8,1676 |
1792,3 |
|
400 |
673,15 |
3277,9 |
8,4597 |
2584,7 |
3277,6 |
8,3882 |
2214,9 |
3277,3 |
8,3263 |
1937,5 |
|
450 |
723,15 |
3382,1 |
8,6090 |
2777,7 |
3381,8 |
8,5376 |
2380,4 |
3381,6 |
8,4757 |
2082,4 |
|
500 |
773,15 |
3487,9 |
8,7505 |
2970,6 |
3487,7 |
8,6791 |
2545,8 |
3487,5 |
8,6173 |
2227,3 |
|
550 |
823,15 |
3595,4 |
8,8852 |
3163,4 |
3595,2 |
8,8139 |
2711,1 |
3595,0 |
8,7521 |
2371,9 |
|
600 |
873,15 |
3704,6 |
9,0140 |
3356,1 |
3704,5 |
8,9427 |
2876,4 |
3704,3 |
8,8809 |
2516,6 |
|
650 |
923,15 |
3815,5 |
9,1375 |
3548,7 |
3815,4 |
9,0662 |
3041,5 |
3815.2 |
9,0045 |
2661,1 |