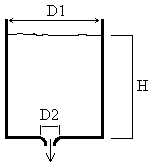
Calcolare la velocità iniziale dell’acqua e il tempo di svuotamento di un serbatoio cilindrico sul cui fondo si trova un foro circolare con i bordi smussati.

I dati del problema sono:

D₁ = (1+0,002 ×CD) m = 1,68 m (diametro del serbatoio)

D₂ = (1/25 D₁) m = 0,0672 m (diametro del foro circolare)

H = (5 + E) m = 10 m (altezza iniziale dell’acqua, dal pelo libero al fondo del serbatoio)

b = 0,5 (coefficiente della perdita di carico concentrata nel foro)

Le richieste:

w₂ = ? (velocità con cui esce l’acqua dal foro all’inizio del processo)

t = ? (tempo di svuotamento del serbatoio)

Per trovare la velocità iniziale w₂, ricorriamo all’equazione di Bernoulli per la conservazione dell’energia, considerando come sezione 1 (entrata) il pelo libero dell’acqua, come sezione 2 (uscita) il foro sul fondo. Abbiamo quindi:

(w₂ + w1) /2 + g(z₂ – z₁) + (p₂-p₁) / r_acqua + R = 0

dove z1 e z2 sono le quote delle due sezioni, g l’accelerazione di gravità e R le perdite di carico.

Notiamo che la velocità del pelo libero dell’acqua all’inizio del processo è nulla e che il processo avviene a pressione atmosferica (non essendo diversamente specificato), quindi otteniamo

(sostituendo a R la formula della perdita concentrata):

w₂/2 – gH + b × w₂²/2 = 0

da cui ricaviamo:

w₂ = [2gH / (1+ b)] = [2 × 9,81 × 10 / (1 + 0,5)] = 11,43 m/s

Notiamo ora che la velocità di svuotamento del serbatoio non si manterrà costante ma diminuirà man mano che l’acqua scende per effetto del minore peso (determinato dalla quantità ‘acqua)che si viene a creare sull’acqua in prossimità del foro. Dovrò quindi considerare per l’altezza dell’acqua durante il processo, una variabile che abbia valori compresi tra H e zero nei vari intervalli di tempo del processo stesso.

Utilizzando la relazione del tubo di Venturi, posso calcolare la velocità del pelo libero dell’acqua:

w₁A₁ = w₂A₂

dove A₁ e A₂ sono rispettivamente l’area delle sezioni 1 e 2 (in particolare, esse sono cerchi);

quindi:

w₁A₁ × p × D₁²/4 = w₂ × p × D₂²/4

da cui:

w₁ = w₂ × (D₂/D₁)²

sostituendo w_{2 troviamo la} velocità dell’acqua man mano che scende:

w1 = [2gH / (1 + b)] × (D₂ / D₁)²

possiamo considerare questo valore in termini infinitesimi di variazione dell’altezza dell’acqua (h) rispetto al tempo:

w₁ = -dh/dt (negativo perché l’acqua scende)

quindi sostituendo a w1 il suo valore avremo:

w₂ × (D₂/D₁)² = -dh/dt

da cui:

dt × w₂ × (D₂/D₁)² = -h^-0,5 × dh

integro i due membri dell’equazione sui valori totali dell’altezza (H) e del tempo (t_tot)

dt × (2g / 1,5) × (D₂ / D₁)² = - h^-0,5 dh

ttot × (2g / 1,5) × (D₂/D₁)² = h^0,5 / 0,5 (in quanto: xⁿdx = xⁿ⁺¹/(n+1)

ttot × (2g / 1,5) × (D₂/D₁)² = 2H

ttot = 2H / [ (2g/1,5) × (D₂/D₁)²] = 210 / [ (2 × 9,81) × (1/25)²] = 1093 s

Calcolare temperatura di saturazione e portata in massa del vapore prodotto in una caldaia piena d’acqua riscaldata da una resistenza.

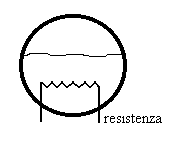
I dati in nostro possesso sono:

Q* = (1000 + EF) W = 1056 W (potenza della resistenza)

p_sat = (10 + C) bar = 13 bar (pressione del vapore saturo contenuto)

Le richieste sono:

T_sat = ?

M*_vap = ? (portata in massa del vapore prodotto in funzione del tempo)

Possiamo subito osservare che avendo già nei dati la pressione, possiamo ricavare dalle tabelle la temperatura di saturazione, che in particolare è:

T_sat = 191°C

La trasformzione in questione è una vaporizzazione (da liquido saturo a vapore secco) a pressione costante. Ci serve quindi conoscere il calore latente di vaporizzazione "r" del liquido che trovo sulle tabelle:

r = 1976 kJ/kg

Notiamo ora che Q* esprime una potenza, quindi è una grandezza che dipende da tempo, e in particolare ci esprime la quantità di calore prodotta in ogni secondo del processo.

Calcoliamo cosa succede in un secondo del nostro processo: osserviamo che la potenza di 1056 W che ho a disposizione corrisponde a 1056 J/s, quindi se considero un solo secondo del processo tale potenza sarà Q = 1056 J.

Dalla definizione sappiamo che r = Q/M, da cui:

M = r/Q

Sostituiamo i valori esprimendo r in J/g:

M = 1056/1976000 = 0,534 g , dove M indica la quantità in massa di vapore prodotto in un secondo del processo. Esprimendo quindi questa grandezza in termini di portata avremo:

M* = 0,534 g/s (portata in massa del vapore prodotto, cioè la quantità di vapore prodotta in ogni unità di tempo)

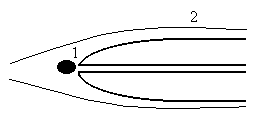
In un aereo è montato un tubo di Pitot sul musetto. Calcolare pressione differenziale e pressione di ristagno del tubo di Pitot.

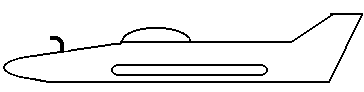
I dati in nostro possesso sono:

u = (700 + 2 × BC) km/h = 746 km/h (velocità dell’aereo)

p_atm = 0,3 + D/20 = 0,5 bar

Le richieste:

Dp = ? (pressione differenziale)

p_R= ? (pressione di ristagno)

Per prima cosa possiamo notare che nel nostro caso la pressione statica p_stat è uguale alla pressione atmosferica.

Applichiamo l’equazione di Bernoulli applicata al tubo di Pitot, considerando come punto 1 l’imbocco del tubo, come punto 2 un punto sulla superficie esterna del tubo stesso; trascuriamo inoltre le perdite di carico R visto che data la grande velocità e la piccolezza del tubo posso essere considerate ininfluenti:

(u₂² – u₁²) / 2 + g × (z₂ – z₁) + (p₂ – p₁) / r_aria + R = 0

ma siccome sappiamo che nel tubo di Pitot all’imbocco del tubo (punto 1) si crea la pressione di ristagno e la velocità del fluido è nulla, e non c’è differenza di quota (z2 – z1) perché consideriamo orizzontale l’avanzamento dell’aereo, otteniamo:

u₂²/2 = Dp/r_aria

da cui ricaviamo:

Dp = r_aria × u₂²/2

dove possiamo notare che u₂ corrisponde alla velocità dell’aereo stesso.

A questo punto dobbiamo calcolare la densità dell’aria r alla quota e alla temperatura prese in considerazione. Sappiamo che la densità è una grandezza che si può esprimere come reciproco del volume specifico del materiale stesso, quindi possiamo applicare all’aria l’equazione di stato dei gas perfetti (ricordando che l’aria è considerata un gas perfetto) per ricavare il volume specifico:

pV = MRT

riferendoci alle grandezze specifiche (e quindi dividendo per l’unità di massa) l’equazione risulta:

pv = RT

ricaviamo dalle tabelle il valore di R per l’aria:

R_aria = 287

Quindi essendo r = 1/v , avremo:

p/r = RT , da cui:

r = p/R×T

Sostituiamo i valori nell’equazione (convertendo in Pascal la pressione prima espressa in bar, per cui sarà: 0,5 bar = 500000 Pa, essendo 1 bar = 10⁵ Pa; convertiamo anche la temperatura in temperatura assoluta -in gradi Kelvin- aggiungendo 273 al valore in gradi centigradi):

r = 500000/287 × 273 = 0,6381 kg/m³

ora dobbiamo convertire la velocità dell’aereo in m/s per avere omogeneità nelle unità di misura, quindi moltiplichiamo il dato per il fattore di conversione che è: 1 km/h = 1000/3600 m/s, per cui avremo:

746 × 1000/3600 = 207,22 m/s

a questo punto sostituisco nella relazione trovata con l’equazione di Bernoulli e ricavo Dp:

Dp = 0,6381 × 207,222/2 = 13071,5 Pa

Da cui posso ricavare ora la pressione di ristagno p_R, essendo Dp = p_R – p_stat:

p_R = p_stat + Dp

avrò:

p_R = 500000 + 13071,5 = 63701,5 Pa

Determinare peso e volume di una massa di aria di assegnata pressione, temperatura ed entalpia.

I nostri dati sono:

p = (2 + D) Pa = 6 Pa (pressione)

t = (50 + EF) °C = 106°C (temperatura)

H = (120 + BC) kJ = 143 kJ (entalpia)

Partiamo dell’equazione di stato dei gas perfetti, essendo l’aria considerata tale:

pV = MRT

consideriamo tale equazione per le unità di misura specifiche (dividiamo quindi per l’unità di massa):

pv = RT

da cui ricaviamo il volume specifico:

v = RT/p

sostituiamo i valori, ricordandoci che la temperatura espressa nell’equazione di stato dei gas perfetti è in termini di temperatura assoluta, quindi in gradi Kelvin (0°C = 273 K), e che la pressione va espressa in Pascal (1 bar = 10⁵ Pa)

v = 287 × (106 + 273) / 600000 = 0,1813 m³/kg

Questo valore esprime però il volume specifico, cioè riferito all’unità di massa, e non conscendo la massa totale non posso sapere direttamente il volume totale. Per ricavare la massa ricorro all’entalpia, considerando h l’entalpia specifica ho:

H = M × h

Per definizione, h si può esprimere come:

h = c_p × t

dove cp esprime il calore specifico a pressione costante ( che nel caso dell’aria: cp = 1000, e t la temperatura espressa in gradi centigradi

avremo quindi: H = M × cp × t , da cui ricavo

M = H / (c_p × t)

Sostituendo (ed esprimendoe in Joule l’entalpia)

M = 143000 / (1000 × 106) = 1,284 kg

Possiamo quindi ricavare oraa il volume totale dal volume specifico:

V = v × M

Quindi:

V = 0,1813 × 1,284 = 0,2329 m³

Ora, sapendo che il peso è dato dal prodotto della massa per l’accelerazione di gravità g, otteniamo:

P = M × g = 1,284 × 9,81 = 12,6 N

ESERCIZIO (tratto dal tema d’esame del 29/6/01)

Determinare la perdita di carico R ed il coefficiente di perdita di carico localizzata b prodotto da un filtro antisabbia, conoscendo il diametro del condotto, la portata di acqua e la caduta di pressione prodotta.

i nostri dati quindi sono:

Dp = (0,03) bar = 0,007 bar (differenza di pressione tra i punti 1 e 2)

D = (20 + C) m = 23 mm (diametro del tubo)

Q_m = (0,3 + 0,05 × D) kg/s = 0,5 kg/s (portata del tubo)

Ci sono richieste:

R = ? (perdita di carico concentrata)

b = ? (coefficiente della perdita di carico concentrata in funzione della geometria del tubo)

Applichiamo anche in questo caso l’equazione di Bernoulli alle sezioni 1 e 2 del tubo:

(w₂ – w₁) / 2 + g × (z₂ – z₁) + (p₂ – p₁) / r + R = 0

possiamo elidere le differenze di velocità (al velocità del fluido è sempre uguale essendo uguale la sezione del tubo) e la differenza di quota (consideriamo il tubo perfettamente orizzontale), per cui ci rimane:

(P₂ – P₁) / r + R = 0

dalla definizione sappiamo che R = b × w²/2 (dove w è la velocità media del fluido) e a anche che R = Dp/r (regola della lunghezza equivalente).

Posso quindi determinare R (sapendo che la densità dell’acqua è: r = 1000 kg/m3)

R = 0,007 / 1000 = 7 kJ/kg

Possiamo ricavare b dalla relazione precedente:

b = (R × 2) / w²

Dobbiamo quindi ricavare w e per questo utilizziamo la definizione di portata (Qm):

Q_m = r × w × A

Dove A è la sezione del tubo; essendo il nostro un tubo cilindrico avremo:

Qm = r × w × p × D²/4

Da cui ricaviamo w:

w = (q_m ×4) / (r × p × D2)

sostituendo i valori:

w = (0,5 × 4) / (1000 × 3,14 × 0,0232) = 1,20 m/s

Posso quindi sostituire i valori nella relazione ottenuta per trovare b e ottengo:

b = (7 × 2) / 1,20² = 9,66

Un alettone da formula 1 dà luogo ad un valore medio della velocità dell’aria sulla sua faccia inferiore più elevato di un fattore k rispetto alla velocità della vettura (300 km/h), mentre sulla sua faccia superiore, piana, si suppone che la velocità dell’aria coincida con quella della vettura. Conoscendo la superficie dell’alettone, determinare la spinta deportante da esso prodotta.

I dati forniti sono:

u₁ = 300 km/h (velocità dell’automobile)

u₂ = k × u1 (velocità dell’aria sotto l’alettone)

k = 1,3 + 0,1 × F = 1,9

A_alettone = (0,5 + 0,5 × x E) m2 = 3 m2

Ci viene richiesta:

F_dep = ? (forza deportante)

Osserviamo che al di sotto dell’alettone si crea una pressione p2 minore della pressione p1 presente al di sopra dell’alettone stesso.

Per calcolare la forza deportante occorre conoscere la differenza di pressione sopra e sotto l’alettone. Visto che abbiamo un caso in cui abbiamo due diverse velocità e due diverse pressioni, utilizziamo l’equazione di Bernoulli:

u₁²/2 + p₁/r_aria = u₂²/2 + p₂/r_aria

in cui abbiamo trascurato le perdite di carico e la differenza di quota (essendo di norma un alettone abbastanza sottile)

da cui ricaviamo la differenza di pressioni:

p₁-p₂ = (u₂² – u₁²) / r_aria

ci occorre ora conoscere la velocità u₂. Per ottenere convertiamo in m/s la velocità u₁ in modo da ottenere omogeneità delle unità di misura nei calcoli seguenti:

u₁ = 300 × (1000 / 3600) = 83,33 m/s

u₂ = k × u1 = 1,9 × 83,33 = 158,33 m/s

posso ora calcolare la differenza di pressione che sarà (ricordando che la densità dell’aria è: r_aria = 1,2 kg/m3):

p₁-p2 = 1,2 × [(158,332 – 83,332) / 2)] = 10784 Pa

sapendo dalle definizione che la forza deportante è espressa dalla formula:

F_dep = Dp × A

Ottengo:

F_dep = 10784 × 3 = 32350 N