Bergonzini
Andrea – matr. 138770 – Lezione del 20/12/2001 – ore 16:00-18:00
Le perdite di carico nei condotti.
Perdite di carico distribuite.
Perdite di carico concentrate.
Metodo di calcolo tramite l’ uso dei coefficienti β.
Metodo di calcolo tramite l’ uso della lunghezza equivalente.
Metodi di calcolo informatici.
Premessa.
Nel processo di astrazione che si attua per operare nel campo della fisica, si cerca di risolvere i problemi del reale al fine di avere a disposizione un sistema che possa governare processi concreti, proponendosi come sostegno logico ed economico.
Nel campo della fluidodinamica si cerca di spiegare situazioni in cui sono direttamente implicati concetti di moto, deformazione e trascinamento di fluidi, diversamente dalla termodinamica classica che fa sempre riferimento all’ equilibrio dei sistemi chiusi. Per arrivare alla soluzione di questioni di fluidodinamica, e più in particolare di quelli legati alle perdite di carico, si è proceduto frequentemente con metodi induttivi, analizzando fenomeni reali per via sperimentale. Il calcolo di tali perdite, essendo una frequentissima applicazione per il dimensionamento di numerosi impianti, sta seguendo un sempre più avanzato sviluppo con modelli di calcolo specifici per ogni azienda produttrice, e programmi informatici ormai in grado di soppiantare diagrammi e tabelle. La ricerca mira quindi a fornire una esaustiva panoramica relativa alla comprensione ed al calcolo del fenomeno delle perdite di carico nei condotti tramite una breve relazione.
Elementi di fluidodinamica.
Generalità.
Per chiarire il campo di applicazione di questa scienza è bene specificare l’ oggetto che viene studiato: i fluidi. Questa categoria comprende la sostanza in stato liquido e gassoso. Nel caso in cui si presenti lo stato liquido è bene ricordare che esso determina che la sostanza assuma un volume costante ( incomprimibile con variazione max. 1%) ma non una forma fissa ( varia con il recipiente ). Nel caso gassoso invece nessuna proprietà fisica viene mantenuta, infatti forma e volume mutano caso per caso. Le grandezze fisiche utilizzate in questo ambito, e le loro unità di misura, sono le seguenti:
-
Velocità 
-
Pressione 
-
Lavoro 
-
Densità 
-
Viscosità 
-
Viscosità cinematica
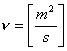
Numero di Reynolds.
Per risalire all’ origine di queste problematiche, e quindi alla loro causa, bisogna fare riferimento ad una serie di esperimenti realizzati da Osborne Reynolds (1842-1912), un celebre fisico inglese che studiò a fondo la fluidodinamica. Egli arrivò a trarre importanti conclusioni dalle sue numerose esperienze di moto dei fluidi, individuando due tipi di moto caratteristici che si possono generare all’ interno di un condotto in pressione. La sua più celebre sperimentazione consisteva nell’ immissione di un liquido tracciante colorato (con caratteristiche simili a quelle del liquido principale) all’ interno di un tubo in pressione, al fine di individuare il suo comportamento rispetto all’ altro fluido trasparente (acqua).
Figura 1. L' esperimento di Reynolds con il diverso comportamento dell' inchiostro.
Il fisico notò che variando determinati parametri del sistema considerato, l’ inchiostro che si immetteva aveva un comportamento diverso. In alcune situazioni esso usciva dal filo proseguendo in linea retta senza mischiarsi all’ acqua in pressione. In altre situazioni l’ inchiostro appena uscito dal tubicino di immissione, si liberava in diverse traiettorie casuali nella tubazione, mischiandosi di fatto col fluido trasparente. Capitava poi che in altre occasioni si avesse una situazione intermedia, con un moto ibrido non ben riconoscibile. La conclusione portò alla definizione di una grandezza espressa da un numero puro che potesse permettere di calcolare in quale situazione (tra le due sperimentate) si trovi un fluido all’ interno di un condotto in qualunque situazione.
Questo numero è detto appunto di Reynolds ed è espresso dalla seguente formula:
(1)
dove D indica il diametro della tubazione.
E utile osservare come si possa generalizzare il comportamento di un filo di inchiostro a quello di un infinitesimo filetto di acqua. Da questo si può affermare che quando il singolo filo viaggia linearmente, ogni filetto avrà un moto analogo, che non interferirà minimamente con il moto del filetto adiacente. Nel caso in cui il filo si disgrega si ha invece una divisione infinitesimale dello stesso che genera piccole traiettorie disordinate che si incrociano altre che si sono innescati negli strati vicini.
Per stabilire se ci si trova nella condizione in cui l’ inchiostro viaggiava linearmente (denominata “moto laminare”) oppure in quella in cui esso si mischiava caoticamente (“denominata moto turbolento”) basta analizzare il valore del numero di Reynolds:
Re < 2100 è moto laminare
2100< Re<4000 è moto ibrido (non idealizzabile)
Moto laminare 
Figura 2. Diagramma della velocità nel moto laminare. Figura 3. Andamento degli strati nel moto laminare.
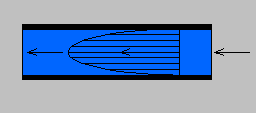
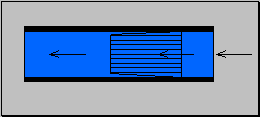Moto turbolento 
Figura 4. Diagramma della velocità nel moto turbolento. Figura 5. Andamento degli strati nel moto turbolento.
Dalla formula (1) è utile osservare che il tipo di moto che si viene ad instaurare in una tubazione non dipende soltanto dalla velocità, ma è caratterizzato anche da altre tre grandezze fisiche. Non esiste quindi una velocità di soglia oltre cui si ha un determinato tipo di moto, ma esiste, piuttosto, un insieme di circostanze tra loro collaboranti.
Teorema di Bernouilli.
Per comprendere il fenomeno delle perdite di carico è indispensabile affrontare il teorema di Bernouilli, che, tramite il principio di conservazione dell’ energia, permette di trovare delle relazioni che legano le proprietà del fluido in sezioni diverse della tubazione. Grazie ad una semplice equazione si possono quindi raffrontare due qualunque settori, eguagliando l’ energia che il fluido possiede nei due differenti istanti. Risulta quindi un uguaglianza tra due sommatorie di energie, in quanto il fluido possiede sempre tre differenti tipi di energia in qualunque posizione si trovi:
-
Energia potenziale dovuta all’ altezza geodetica z 
(2)
-
Energia potenziale dovuta alla pressione interna p 
(3)
-
Energia cinetica dovuta alla velocità c 
(4)
Con P che rappresenta il
peso del fluido.
Di conseguenza ogni punto possiederà una energia totale E pari a:
(5)
Eguagliando le energie di due punti differenti avrò:
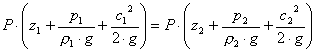(6)
Semplificando, dividendo per P, moltiplicando per g:
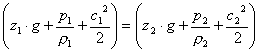(7)
Perdite di carico.
Generalità.
Al fine di ricondurre queste considerazioni all’ ambito delle perdite di carico, è bene fare una fondamentale osservazione:
se ci si trova in un regime di moto laminare ,con gli strati di scorrimento paralleli, il liquido viaggerà liberamente, mentre se i filetti tendono a mischiarsi (moto turbolento), seguirà che inevitabilmente essi dovranno vincere le forze di attrito che si generano in questo moto caotico. Queste forze negative determinano sempre, infatti, un calo di pressione e sono direttamente proporzionali alla viscosità del liquido, in quanto rappresentano i legami da sciogliere che si sono instaurati tra le particelle del fluido, o tra il fluido e le pareti del condotto. Inoltre incide sul risultato anche la scabrosità delle pareti, che invece non influenza minimamente il moto laminare. Considerato che la maggior parte della casistica odierna degli impianti è basata su moti turbolenti (eccezion fatta per alcuni movimenti di oli combustibili), risulta indispensabile affrontare adeguatamente il problema delle perdite di pressione, per dimensionare correttamente, in un secondo tempo, tubazioni, accessori e macchinari.
Trovandoci invece ad esaminare moti turbolenti ( ricordiamo Re > 4000 ) bisogna rivedere le equazioni generali della fluidodinamica, essendo esse applicate a casi ideali. Dovremo quindi riadattare il teorema di Bernouilli.
Introducendo la formula nel contesto reale dei condotti avrò:
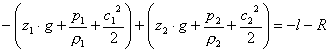(8)
dove -l è il lavoro o energia tolta o data da eventuali dispostivi meccanici d’ ausilio ( pompe o turbine in genere ) e dove –R sono le perdite di carico totali del tratto. Il segno di queste due grandezze è negativo in quanto si suppone che i dispositivi, solitamente, sottraggano energia, così come fanno le perdite di carico. Essi quindi assumerebbero già valori di per sé negativi.
Entrando nel particolare arriviamo dettagliatamente ad analizzare il valore di R, che, vedremo, è composto da due diversi tipi di perdite di carico: distribuite (o continue) e concentrate (o localizzate).
(9)
Perdite di carico distribuite.
Le perdite di carico o di pressione distribuite sono riconducibili al lavoro speso da un fluido per percorrere un determinato tratto di tubo orizzontale continuo. Questo lavoro sarà quindi direttamente proporzionale alla viscosità del fluido (per vincere le tensioni interne) e alla scabrosità delle pareti (per vincere l’ attrito). Più precisamente diremo che le perdite distribuite sono in funzione di:
(10)
dove ε è un valore di scabrezza delle superfici bagnate, D il diametro della tubazione e Re il numero di Reynolds.
In particolare il valore di ε rappresenta il dislivello medio intercorrente tra le gola e le punte estreme della scabrosità del condotto:
Figura 6. Scabrosità
ε delle pareti. N.B.: (E*=ε).
Il diametro D invece, se non si è in un caso con condotto a sezione circolare, va calcolato tramite una relazione che individua un diametro equivalente a cui ricondurre qualsiasi genere di sezione.
Tale equivalenza è data da:
(11)
dove A rappresenta l’ area della sezione generica, e 2p il perimetro costantemente bagnato dal fluido. E bene ricordare che nei nostri casi ci si riconduce sempre a condotti in pressione pieni, che hanno quindi tutto il loro perimetro a contatto col fluido. Per meglio comprendere la (11) basti pensare a questa esemplificazione di un sistema con canale aperto:
Figura 7. Passaggio da una sezione qualunque al diametro equivalente.
Per il calcolo dei valori delle cadute si fa ricorso a metodi empirici, che misurano semplicemente gli sbalzi di pressione in entrata e in uscita da una tubazione di lunghezza data.
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Per dimostrare ciò si presenta una facile esemplificazione:
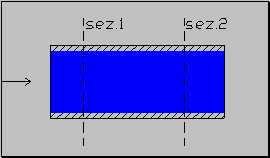
Figura 8. Condotto orizzontale regolare.
Provo ad applicare la formula di Bernouilli per capire cosa succede nelle due sezioni:
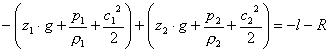(12)
Essendo 
e 
e l=0 potrò
semplificare per ottenere:
è 
(13)
con sicuramente 
.
Da ciò si otterrà facilmente la fondamentale relazione:
(14)
:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Si introduce ora la formula di uso corrente per il calcolo delle perdite di carico distribuite:
(15)
dove λ è detto fattore di attrito, e si calcola differentemente a seconda del regime di moto.
Nel caso di regime di moto laminare, λ sarà esprimibile esclusivamente in funzione del numero di Reynolds. Vale a dire:
(16)
più specificatamente, proprio nel caso di moto laminare avrò:
(17)
Quindi riconducendoci alla dicitura del tipo di (16):
(18)
con
Da questo si evince che il diametro del condotto, la natura del fluido, e la velocità del moto influiscono sul fattore di attrito λ solo nella misura in cui questi modificano il numero di Reynolds.
Inoltre le perdite di carico sono direttamente proporzionali al quadrato della velocità (se la velocità è nulla infatti non si hanno cadute) e al coefficiente λ oltre che alla geometria del condotto ( l/D ).
Nel caso di moto turbolento però bisogna effettuare una modifica nelle formule applicative, in quanto bisogna considerare che il coefficiente λ è questa volta in funzione sia del numero di Reynolds, che della scabrosità delle pareti ε (che prima non interferiva).
Più in particolare diremo che λ è dato da:
(19)
dove ε/D è definita scabrosità relativa, in quanto è rapportata al diametro del condotto.
Essendo λ espresso in funzione di due numeri puri, anch’ esso sarà tale.
Per governare questa complessa funzione si è tracciato un diagramma (detto di Moody, a coordinate doppio-logaritmiche) che riporta sulle ascisse i valori in entrata di Re, e sulle ordinate i relativi valori di λ. Per calcolare il λ desiderato basta infatti conoscere Re, salire lungo questo valore fino alla curva della funzione corrispondente al valore di scabrosità relativa che si ha nel tubo, e determinare λ come ordinata del punto d’ incontro.
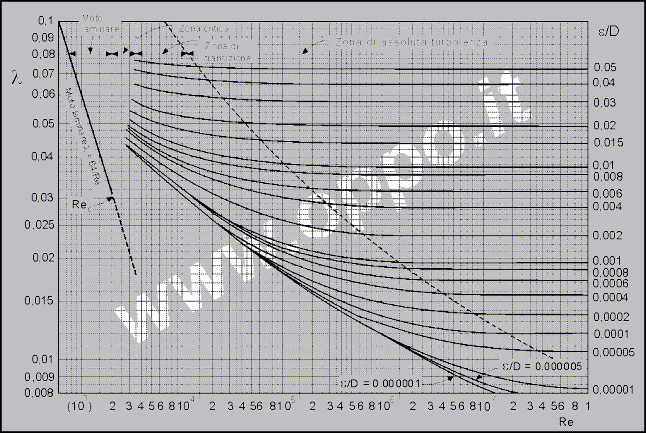
Figura 9. Diagramma
di Moody per il calcolo del fattore di attrito λ. Dal sito internet www.oppo.it/calcoli/moodys.html
*E
bene sottolineare come questo grafico adotti la dicitura di zona critica per
indicare il moto ibrido e di zona di transizione per indicare un moto non
ancora perfettamente turbolento, ma che in realtà può effettivamente
considerarsi tale.
Dal diagramma possiamo anche trovare riscontro delle differenze introdotte precedentemente tra moto laminare e turbolento per il calcolo delle perdite distribuite. Nel grafico abbiamo infatti 4 zone principali, indicate dalle frecce in alto. Esse non sono altro che le sezioni comprese tra i valori limite del numero di Reynolds riportati in coordinate logaritmiche in ascissa:
moto laminare Re < 2100
zona critica 2100 < Re < 4000
zona di transizione 4000 < Re < 10000
moto turbolento Re > 10000
Se si prendono quindi valori di Re minori di 2100 si
dovrà sempre fare riferimento all’ unica linea retta inclinata presente in
quell’ intervallo, per il calcolo di λ.
Per valori di Re in zona critica, non si può ben decifrare il comportamento dinamico del fluido infatti la linea precedente risulta tratteggiata in corrispondenza di questo intervallo.
Generalmente per valori di Re superiori a 4000 si fa riferimento alla parte più complessa del diagramma. Dopo aver infatti scelto il valore di entrata in ascissa (ovviamente > 4000) si sceglie la curva nella parte superiore del grafico che fa riferimento al valore di scabrosità relativa della tubazione utilizzata ( i valori sono riportati nella parte destra del grafico ). In questo regime di moto non si fa quindi più riferimento ad una sola funzione lineare, ma a più curve, riferite ad ogni valore tipico di ε/D.
E utile notare come per valori di Re molto alti, in regime di moto altamente turbolento, le curve del grafico tendano a diventare orizzontali. Da questo si deduce che in moti molto turbolenti, conoscendo la scabrezza del tubo, si può trovare il valore del fattore di attrito λ, anche senza conoscere l’ esatto numero di Reynolds Re.
Per determinare il valore delle perdite distribuite sarà quindi necessario conoscere la geometria della tubazione, la velocità del fluido e il valore del numero di Reynolds, sfruttando il principio della similitudine che impone uguaglianze geometriche e dinamiche per ottenere tipologie di moto analoghe.
Perdite di carico concentrate.
Nel calcolo di reti impiantistiche reali si ha sempre a che fare con una serie di percorsi che prevedono numerose discontinuità all’ interno della tubazione. E infatti necessario tenere conto di ciò che differenza il condotto da esaminare, rispetto al tragitto ideale rettilineo orizzontale ed uniforme. Le più frequenti discontinuità che si incontrano, infatti, contribuiscono a generare forti turbolenze anche in presenza di moti di fluidi con un basso valore di Re. E quindi importante studiare quali modifiche apportano tali disomogeneità di sezione all’ andamento dinamico del fluido. Considerando, come nel caso precedente, che non si hanno vere teorie che governano la materia in esame, si vuole qui elencare le modalità di calcolo derivate da differenti esperimenti.
E bene innanzitutto definire l’ oggetto che causa queste cadute: curve, valvole, rubinetti e contatori possono tutti considerarsi elementi che frappongono una discontinuità al percorso ideale di un fluido all’ interno di un condotto.
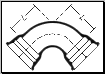
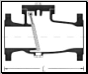
Figura 10. Esempi di discontinuità tipiche dell’ impiantistica.
Curva a 90°, strozzatura e valvola di ritegno a battente gommato.
Nel caso di curve è facile prevedere un diverso comportamento del fluido all’ uscita da queste, ma è sperimentato che una qualsiasi discontinuità rispetto alla sezione standard prima esaminata possa generare una perdita di pressione. Non seguono infatti fenomeni nuovi in queste circostanze, ma bensì si generano solamente moti altamente turbolenti che vanno quindi a determinare una forte perdita di pressione come avveniva per le perdite distribuite. La differenza sta appunto che in questo caso le perdite sono concentrate in una sezione essenzialmente puntiforme, mentre prima erano dislocate entro tutto il tracciato.
Metodo di calcolo tramite l’ uso dei coefficienti β.
Per comprendere il metodo di calcolo basta fare un semplice confronto. Se nel caso di perdite continue si aveva:
(20)
ora
per le perdite concentrate si avrà una variazione non più rispetto a Re (
che si è visto, risulta quasi ininfluente ) ma rispetto ad un nuovo
coefficiente β:
(21)
Più precisamente si avrà la formula:
(22)
Tale fattore β può altresì essere definito come un nuovo fattore di attrito. Esso varierà però solo ed esclusivamente in relazione al tipo di discontinuità che il fluido dovrà affrontare. Sempre per via sperimentale si sono determinati valori fissi di β per ogni accidentalità tipica, e si sono riportati in una tabella unica per una rapida consultazione.
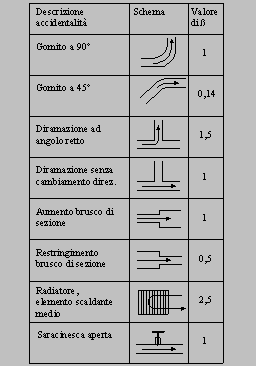
Figura 11. Tabella dei coefficienti β.
E utile osservare che, nel caso di discontinuità causate da meccanismi mobili (saracinesche, rubinetti ecc…), il coefficiente β è sempre variabile a seconda del loro grado di apertura. Nella tabella è sempre indicato il valore nel caso in cui il marchingegno sia completamente aperto, ma si può dedurre che aumentando l’ ostruzione del decorso naturale del liquido, β aumenterà fino ad assumere un valore infinitamente grande (è∞) nel caso in cui il passaggio del fluido sia impedito totalmente.
Per utilizzare questo metodo di calcolo basta quindi conoscere la velocità del fluido e il tipo di discontinuità incontrate.
Per trovare la variazione di pressione tra entrata e uscita, basta applicare la (14).
Metodo di calcolo tramite l’ uso della lunghezza equivalente.
Per velocizzare i calcoli dei progetti di reti impiantistiche si è introdotto un nuovo metodo di calcolo delle perdite concentrate che tiene conto di una importante intuizione. Una discontinuità infatti fornisce sempre una data perdita di carico che potrebbe anche essere causata ugualmente da una determinata lunghezza di tubazione tipica, visto che anche un condotto orizzontale standard fornisce cadute di pressione, seppur minori. Si procede quindi sostituendo alla discontinuità un opportuno valore di lunghezza virtuale di condotto standard come nell’ esempio:
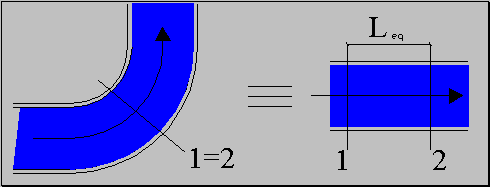
Figura 12. Schema di ragionamento per la lunghezza equivalente.
Intuitivamente visto che la lunghezza l reale del tubo comprende anche la lunghezza degli eventuali tratti discontinui (gomiti ecc..) sarà necessario andare a sommare le lunghezze equivalenti di tutte le accidentalità alla misura l reale totale. La nuova misura fittizia così ottenuta sarà così definita da:
(23)
Le lunghezze equivalenti relative
ad ogni tipo di accidentalità si trovano gabellate o descritte da appositi
diagrammi.
Questo tipo di calcolo essendo
basato su principi sperimentali non presenta una assoluta precisione, ma
bisogna appuntare che le varie aziende produttrici di condotti forniscono loro
stesse questi valori di perdite di carico, dopo aver effettuato test attendibili
sui loro prodotti.
Un esempio di tabulato riferito a
tubi in rame può essere questo:
|
Ø |
Saracinesca |
Curva piccolo raggio |
Curva grande raggio |
Diramaz. Rettil. |
Convergenza T |
|
¾” |
0,20 |
0,40 |
0,30 |
0,30 |
1,2 |
|
1 ¼” |
0,30 |
0,65 |
0,45 |
0,45 |
1,8 |
Figura 13. Tabella per lunghezze equivalenti delle discontinuità nei tubi in rame.
Un nomogramma empirico molto diffuso, che fornisce risultati per via grafica può essere simile a quello di seguito riportato.
Il procedimento di determinazione della lunghezza equivalente avviene leggendo il valore di intersezione nella scala di mezzo, dopo aver unito con una linea retta i valori scelti sulle due scale esterne.
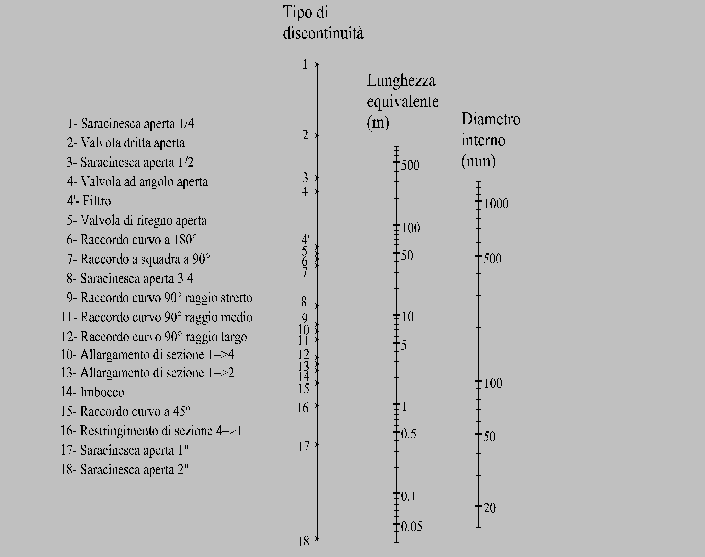
Figura 14. Nomogramma per la determinazione grafica delle lunghezze equivalenti delle più diffuse accidentalità dei condotti.
Basterà quindi andare a calcolare normalmente solo le perdite di carico distribuite tramite la (15) , in quanto ci si è ricondotti ad un caso virtuale in cui le cadute di pressione sono innescate solamente da perdite continue. L’ unica differenza rispetto alla (14) si avrà nel valore di l che sarà sostituito da l* (>l) ottenendo:
(24)
Vale
a dire che la perdita di carico totale per l’ intera tubatura è descrivibile
con la relazione:
(25)
Metodi di calcolo informatici.
Con l’ avvento dell’ informatica anche questo ramo della fisica sta seguendo la via della digitalizzazione dei calcoli al fine di permettere economia di spazi e tempi agli attuali progettisti.
Per determinare le perdite di carico, sono in circolazione numerosissimi programmi di dimensioni ridotte, che permettono di avere calcoli rapidi e personalizzati direttamente dalle aziende.
Si forniscono di seguito alcuni links utili per il download di questi programmi gratuiti:
OPPO. Calcolo perdita di carico Hazen-Williams
OPPO. Valutazione delle perdite di carico
OPPO.Tabelle Perdite di carico.
Si allega anche un semplice programma della ditta Dalmine in cui è sufficiente scegliere il tipo di calcolo e riempire i campi liberi per ottenere il risultato. E visualizzabile cliccando qui.
Esercitazioni.
Esercizio 1
Figura 15. Schema dell’ esercizio 1.
Dati:
H = 2m ; Ø = 2 cm
; l = 4 m ; 
; 
; 
; 
; 
; 
Provo ad utilizzare la formula (8) di Bernouilli per le tubazioni per capire cosa succede all’ interno del sistema. Avrò:
(26)
In questa equazione avrò:
- l=0 in quanto non ci sono dispositivi esterni che influiscono sull’ energia del moto.
- 
in quanto le due pressioni sono uguali alla pressione atmosferica
di 100.000 Pa.
- 
- 
- 
- La velocità all’ uscita che è uguale alla velocità all’ interno di tutto il condotto.
Semplificando otterrò quindi una nuova relazione da cui ricavo la velocità all’ uscita:
(27)
L’ incognita di questa equazione è però il valore del fattore di attrito λ, che, come visto nella (16), dipende dal numero di Reynolds Re, che a sua volta si calcola con la (1) in funzione di w. Non possiamo quindi applicare questa formula direttamente, ma servono dei ragionamenti. Il problema si può comunque risolvere in 2 modi:
1° MODO
Calcolo la scabrezza relativa:
Ipotizzo che all’ interno del tubo si generi un moto perfettamente turbolento. In questa situazione abbiamo infatti nel diagramma di Moody che il fattore di attrito λ rimane costante sulla curva scelta ε/D, a prescindere dal valore di Re ( che sarà comunque molto alto ).
Ricavando graficamente il fattore di attrito si avrà: λ = 0.038
Conoscendo il valore di λ si può quindi procedere al calcolo della velocità tramite la (27):
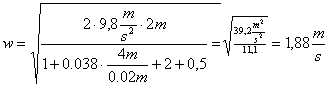
2° MODO
In questo caso si vuole procedere per iterazione, vale a dire ipotizzando una velocità plausibile e ricalcolandola fino a quando non si sarà approssimata al valore ipotizzato.
Si procede per passi:
-
Ipotizzo 
*=2,2 m/s
- Calcolo il valore di λ con la (27) ricavando:
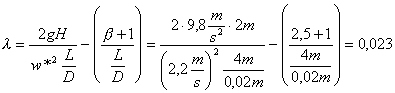(28)
- Calcolo il numero di Reynolds Re con la (1):
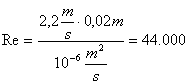
- Ricavo λ dal diagramma di Moody in funzione di Re=44.000 e ε/D=0.001. Ottengo il nuovo valore λ = 0,0247.
- Ricalcolo w con la (27):
-
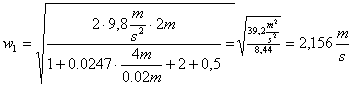
Osservo che la nuova velocità 
calcolata è diversa
da quella ipotizzata 
*.
-
Per questo proseguo l’ affinamento del calcolo
ipotizzando la nuova velocità 
. Proseguo questo procedimento fino a quando non avrò: 
.
Si riporta di seguito una tabella che schematizza l’ intero itinerario di calcoli effettuato:
|
Tentativi |
|
Re |
λ |
|
|
1° |
2,2 |
|
0,023 |
2,2 |
|
2° |
2,2 |
44.000 |
0,0247 |
2,156 |
|
3° |
2,156 |
43.000 |
0,025 |
2,156 |
Figura 16. Tabella del procedimento di iterazione.
L’ ultimo i-esimo valore di w sarà quello che effettivamente si genera all’ interno del condotto.
CONCLUSIONE
I due risultati sono diversi in quanto il primo teneva erratamente conto che il moto fosse in regime fortemente turbolento. Il numero di Reynolds calcolato nel secondo metodo più preciso smentisce questo presupposto. Il valore da considerare giusto è quindi solo il secondo:
w = 2,156 m/s
N.B.: se ci fossimo trovati in regime molto turbolento con Re>>100.000 i due risultati sarebbero stati entrambi validi e coincidenti.
La portata in volume si calcolerà poi in funzione di w come:
(29)
Se consideriamo questi calcoli applicati ad un calcolo reale
di progetto, potremmo chiederci quale sarebbe, ad esempio, il diametro da
scegliere, per avere in uscita una portata di 
.
Per risolvere il problema basta ricavare l’ area A della sezione dalla (29) o più direttamente il diametro D. Vale a dire:
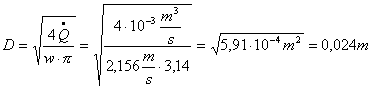
Il diametro da scegliere sarà quindi:
Ø = 0,024m = 2,4 cm
Esercizio 2
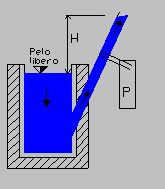
Figura 17. Funzionamento del sistema.
Dati:
H = 50m ; L = 1 Km
; Ø = 100 mm ; μ = 8,5 poise ; 
; 
Prima di tutto si convertono le unità di misura non S.I.:
μ = 8,5 poise = 0,85 Pa s
Per procedere con i calcoli si farà uso del teorema di Bernouilli nei condotti (8) che con le adeguate semplificazioni (pressioni uguali) si presenterà nella seguente forma:
(29)
Si procede calcolando la velocità in uscita (quella iniziale è nulla) da inserire poi nella (29):
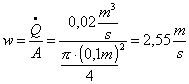
Per determinare il tipo di moto che si genera all’ interno del condotto calcolo il numero di Reynolds:
Le perdite di carico in questo caso sono solo di tipo continuo, infatti per una lunghezza di 1 Km non incidono significativamente le 2 esigue discontinuità di imbocco ed uscita. Trovandoci in regime laminare ( λ = 64/Re = 0,23 ) per la (15) avrò che le perdite di carico saranno:
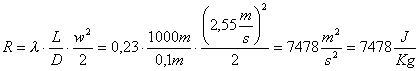
Dalla relazione (29) di Bernouilli
potrò dunque calcolare il lavoro per unità di massa (o specifico) 
della pompa:
Per calcolare la potenza che deve possedere la pompa calcoliamo:
Per trasferire il fluido nel punto finale del condotto, garantendo una portata di 20 l/s servirà installare lungo la tubazione una pompa di potenza specifica pari a 147KW.
FINE