Le perdite di carico

Argomenti trattati:

· Perdite di carico distribuite

· Fattore di attrito

· Diagramma di Moody

· Perdite di carico concentrate

· Lunghezza equivalente

Perdite di carico distribuite

In un tubo in cui scorre un fluido le perdite di carico sono equivalenti alle cadute di pressione. Le perdite di carico possono essere di due tipi differenti: distribuite e concentrate ( o localizzate ). Occupiamoci delle prime.

Le perdite di carico distribuite sono definite in questo modo perché si considerano, appunto, distribuite lungo il tubo stesso. Esse sono da imputare al fatto che il tubo che si considera non è mai ideale: la sua superficie non è perfettamente liscia ma ha una certa rugosità, il condotto ha una sua forma propria che può anche variare, e così via.

Per calcolare questo tipo di perdite si utilizza un’equazione in cui la variazione di pressione è espressa in funzione della velocità (1):

₍₁₎

(fig.1)

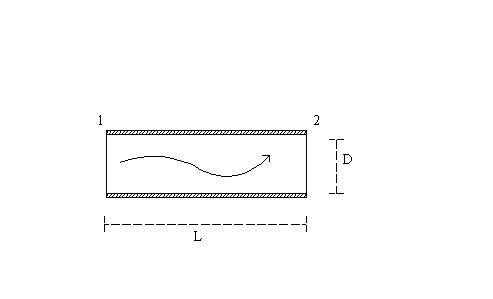
Nella relazione (1) w rappresenta la velocità media di percorrenza del fluido nel tubo, m è la viscosità del fluido, mentre L e D sono rispettivamente la lunghezza e il diametro del condotto considerato, come si osserva in figura (fig. 1). Di queste grandezze, w è misurabile attraverso gli appositi strumenti, m è tabellata e le rimanenti sono facilmente ricavabili.

Dall’equazione (1) si nota che la caduta di pressione, e quindi la perdita di carico, è inversamente proporzionale al quadrato del diametro del tubo, mentre è direttamente proporzionale alla velocità del fluido. Perciò, più il fluido scorre veloce, più energia viene dissipata e maggiore è la perdita di carico. Si può inoltre notare che le perdite di carico risultano proporzionali alla lunghezza del tubo, ed è per questo motivo che vengono dette distribuite lungo tutto il condotto.

E’ bene ricordare che la relazione (1) vale solo per i condotti a sezione circolare; per questa ragione è utile esprimere le perdite di carico in funzione del numero di Reynolds (2):

₍₂₎

La relazione (1), con gli opportuni calcoli, risulta quindi espressa in questa forma (3):

₍₃₎

dove r rappresenta la densità del fluido.

Fattore d’attrito

Nella relazione (3) il numero 64/Re prende il nome di fattore d’attrito e viene indicato con la lettera x. Il fattore d’attrito non è costante, ma varia a seconda della sezione del condotto; il valore 64/Re corrisponde al fattore d’attrito nei tubi a sezione circolare. Perciò, l’espressione (3) generalizzata e resa valida per i condotti di qualunque sezione risulta:

₍₄₎

Il fattore d’attrito non dipende solo dalla sezione del condotto e dal numero di Reynolds, ma varia anche in funzione del tipo di lavorazione del tubo, cioè della rugosità delle sue pareti. Infatti, le asperità che si trovano sulla superficie del tubo contribuiscono alle perdite di carico, ovvero al calo di pressione del fluido.

Diagramma di Moody

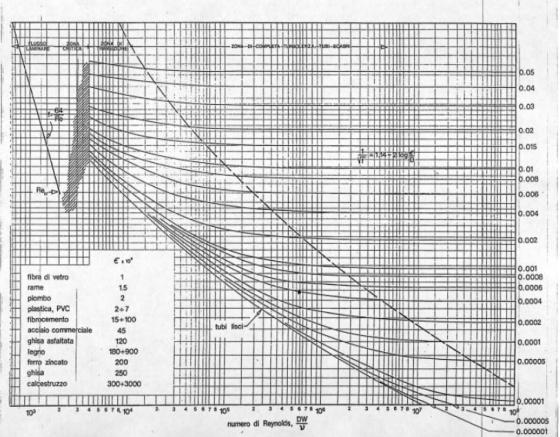
I valori del fattore d’attrito, inteso come funzione del numero di Reynolds e della rugosità ( o scabrezza ) relativa, sono tabulati, e questa funzione viene anche rappresentata graficamente attraverso un diagramma, detto diagramma di Moody (fig. 2).

Nel diagramma sono riportati in ascissa il numero di Reynolds e in ordinata il fattore d’attrito. Ad ognuna delle curve disegnate nel diagramma corrisponde un valore di rugosità relativa del condotto, indicata con il rapporto

in cui D rappresenta il diametro del tubo, mentre e rappresenta l’altezza media delle asperità presenti sulla superficie del tubo.

(Fig.2)

Il diagramma di Moody viene solitamente suddiviso in tre zone:

· la prima è definita dal regime laminare e arriva fino a Re = 2300; in questa zona la curva è una retta

· la seconda è una zona di transizione in cui non si conosce l’andamento del diagramma

· la terza è definita dal regime turbolento e inizia per Re = 4100; in questa zona, per valori abbastanza alti di rugosità relativa, la curva assume un andamento simile a quello di una retta parallela all’asse delle ascisse.

Quindi, se in un problema sono dati il numero di Reynolds e il valore di scabrezza relativa del condotto, grazie al diagramma di Moody si può facilmente ricavare il valore del fattore d’attrito cercato: basta immaginare di tracciare una riga verticale che parte dal valore di Re e arriva alla curva che rappresenta la rugosità relativa del condotto, e quindi, da quel punto, tracciare una riga orizzontale fino al valore del fattore d’attrito desiderato. Se il numero di Reynolds è un’incognita del problema si deve procedere alla risoluzione per tentativi.

Vediamo un esempio.

PROBLEMA

Si calcoli la perdita di carico di un tubo a sezione circolare avente un diametro D = 50.8 mm, una lunghezza L = 22.86 m, nel quale scorre un fluido la cui temperatura T = -12.2°C e la cui velocità media w è di 21.3 m/s. La scabrezza del condotto e è di 0.46 mm, la viscosità del fluido m è e la sua densità r è .

Risoluzione

Per calcolare la perdita di carico nel condotto si utilizza la relazione (4) e, poiché il fattore d’attrito è funzione del numero di Reynolds e della rugosità relativa, per prima cosa si trova Re:

Si può notare che, essendo il valore di Re alquanto elevato, il moto di questo fluido all’interno del condotto è fortemente turbolento.

Si può trovare ora il valore della scabrezza relativa del tubo:

Avendo trovato questi due valori, dalla lettura del diagramma di Moody si ricava facilmente il fattore d’attrito x, che risulta:

Allora, applicando la relazione (4), si ottiene che:

Quindi, la perdita di carico distribuita verificatasi tra la sezione d’ingresso e quella di uscita è pari a 4580 Pa; ciò significa che è andata persa dell’energia, dispersa dal tubo sottoforma di calore.

Perdite di carico concentrate

Un fluido che scorre in un condotto è soggetto a cadute di pressione dovute non soltanto a perdite di carico distribuite, ma anche a perdite di carico dette concentrate o localizzate. Questa denominazione deriva appunto dal fatto che esse sono localizzate in punti precisi del condotto e non sono quindi considerate distribuite lungo il tubo stesso. Ad esempio, si verificano in corrispondenza di curve, gomiti, valvole, rubinetti, restringimenti o allargamenti della sezione del tubo.

Per calcolare le perdite di carico concentrate si utilizza un’espressione coerente con quella delle perdite distribuite; a differenza di queste, però, nell’equazione delle perdite di carico concentrate scompare il termine L/D, proprio perché questo tipo di perdite non dipende dalla lunghezza del condotto. Indicando con b il fattore d’attrito, l’espressione risulta:

₍₅₎

in cui w rappresenta la velocità media di scorrimento del fluido, mentre r è la sua densità. Quando si considera il condotto in tutta la sua lunghezza, si deve tener conto di tutte le perdite di carico concentrate che si verificano lungo il tubo. L’equazione (5) viene quindi espressa con una sommatoria:

I valori di b per i casi più comuni sono riportati in una tabella (fig. 3), che affianca a ogni valore del fattore d’attrito il suo caso specifico di perdita di carico.

(Fig.3)

Da questa tabella si legge, ad esempio, che b può variare tra 0.3 e 0.5 in una curva a gomito mentre vale 2 in una diramazione a T; vale 0.5 se il condotto aumenta la sua sezione e 1.5 se si restringe; vale 0.4 in una valvola a saracinesca e 2.5 in una caldaia, e così via.

Si possono risolvere in questo modo alcuni problemi, come la determinazione di una pompa che occorre per trasportare acqua da un serbatoio posto a una quota inferiore, a un serbatoio posto più in alto; oppure la pompa che occorre per mantenere in circolazione l’acqua in un impianto di riscaldamento.

PROBLEMA

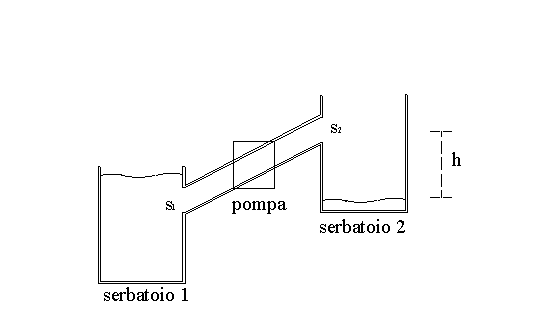
Si calcoli il salto di pressione che deve essere prodotto da una pompa per far scorrere un fluido in un tubo, di diametro D = 100 mm, di lunghezza L = 1 km e la cui portata in volume è pari a 20 l/s, e portarlo così dal serbatoio 1 al serbatoio 2, che si trova ad un’altezza H = 50 m rispetto al primo. La densità del fluido è r = 920 kg e la sua viscosità è m = 8.5 poise.

(Fig.4)

Risoluzione

Per prima cosa si scrive l’equazione di Bernoulli e se ne analizzano i termini:

perdita di perdita di perdita di

pressione pressione pressione

dovuta dovuta dovuta

all’energia all’energia all’energia

cinetica potenziale di carico

In questo caso, w₁, che è la velocità media di entrata in s₁, è nulla; p₁=p, poiché equivalgono entrambe alla pressione atmosferica; (z₂-z₁) è la differenza di altezza tra i due serbatoi, cioè H. L’equazione di Bernoulli risulta quindi semplificata:

Si calcolano, poi, i diversi termini dell’equazione. Per calcolare la velocità media w ( cioè ), si utilizza la relazione che lega quest’ultima alla portata in volume del tubo, che è nota:

Si calcola, infine, l’altro termine ignoto, R, relativo alle perdite di carico; si considerano queste ultime come perdite di carico distribuite. Inoltre, non essendo fornita la scabrezza relativa del condotto, si suppone il tubo a sezione circolare liscio. Si utilizza quindi la formula (3):

₍₃₎

Dopo aver calcolato il numero di Reynolds

lo si sostituisce nella (3):

Si può notare che, essendo il numero di Reynolds piuttosto basso, il moto del fluido all’interno del condotto è di tipo laminare.

Andando ora a sostituire nell’equazione di Bernoulli i valori trovati, si ottiene una caduta di pressione che è quella che deve essere prodotta dalla pompa per far scorrere il fluido da un serbatoio all’altro.

A questo sistema si dovrà quindi fornire una pompa da 7,3× 10⁶ Pa

Lunghezza equivalente

Quando lungo un condotto si verificano sia delle perdite di carico distribuite sia delle perdite di carico concentrate, per calcolare la perdita di carico totale, anziché sommare alle perdite di carico distribuite ogni singola perdita di carico concentrata, si può utilizzare il metodo della lunghezza equivalente. In pratica, è possibile assimilare ad ogni perdita di carico concentrata che si verifica in un punto del condotto, una perdita distribuita in un condotto dello stesso diametro e con un certo valore di lunghezza, detta appunto lunghezza equivalente.

La relazione (5), che esprimeva le perdite concentrate, si converte nella relazione (4) usata per le perdite distribuite, con la sola sostituzione della lunghezza equivalente al termine L:

Per calcolare la perdita di carico totale basterà utilizzare direttamente la formula (4) sostituendo al termine L la somma L+ L_eq, dove L_eq rappresenta la somma delle lunghezze equivalenti di tutte le accidentalità presenti nel condotto.

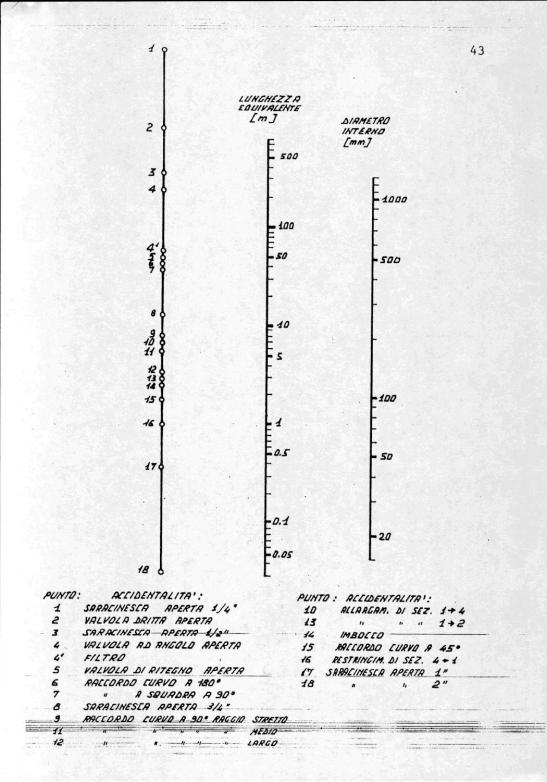
Per calcolare la lunghezza equivalente si utilizza il diagramma in figura (fig. 5):

(Fig.5)

Il diagramma è costituito da tre assi verticali paralleli: su quello di destra si leggono i valori del diametro interno della sezione del tubo in millimetri, su quello di sinistra sono riportati i valori corrispondenti alle accidentalità del tubo e su quello centrale si trova la lunghezza equivalente, espressa in metri. Conoscendo il diametro interno del tubo e il tipo di accidentalità si ricava facilmente il valore della lunghezza equivalente congiungendo con una retta i due punti sugli assi esterni del diagramma corrispondenti ai valori noti: il valore di lunghezza equivalente si trova nel punto d’intersezione di questa retta con l’asse centrale.