Sonia Valente
Matricola 139047
Lezione del 29/11/2001 14:30-16:30
Come introduzione alla mia
trattazione mi permetto di introdurre il concetto di SISTEMA FISICO: si tratta
di un elemento dotato di confine o più semplicemente posiamo considerarlo una pelle
che assemblato all'ambiente sarà destinato a formare l'universo. Questo sistema
però è da considerarsi suddiviso in due parti che si distinguono in quelli che
chiamiamo SISTEMA CHIUSO e SISTEMA APERTO i quali si distinguono, nel campo dei
fenomeni relativistici, attraverso una diversa produzione di leggi fisiche
conseguenti ai differenti tipi di approcci.
SISTEMA CHIUSO
Definiamo SISTEMA CHIUSO un
sistema reale o fittizio all'interno del quale avvengono solo scambi di lavoro
e di calore e la massa rimane costante.
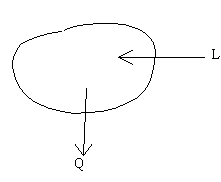
Esistono
tre semplici ma significative equazioni che mi definiscono un sistema chiuso:![]()

dove
per ![]() intendiamo
l'energia interna che si ottiene in conseguenza agli scambi energetici, Q si riferisce al calore ed L al lavoro.
intendiamo
l'energia interna che si ottiene in conseguenza agli scambi energetici, Q si riferisce al calore ed L al lavoro.
Da
notare le simbologie adottate: le lettere vengono scritte maiuscole nel casi si
adottino casi globali mentre sono minuscole durante il loro utilizzo in casi
specifici.
Lezione del 29/11/2001-14:30 16:30
SISTEMA APERTO
Possiamo
paragonare un sistema aperto ad una pelle in cui sono presenti dei buchi, che
contrariamente al sistema chiuso la massa all'interno di esso può cambiare così
come possono presentarsi scambi di lavoro (più specificatamente possiamo
parlare di lavoro di tipo tecnico, che avviene cioè attraverso dispositivi),
mentre l'unica proprietà che rimane invariata è il volume. 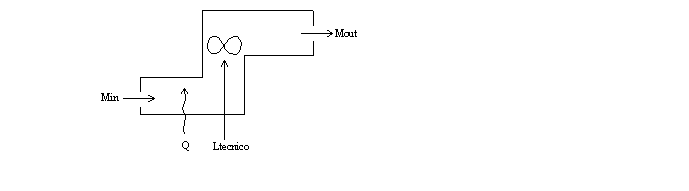
Così
come per il i sistemi chiusi i metodi di indagine termodinamica possono essere
elaborati anche per i sistemi aperti attraverso l'utilizzo di un particolare
sistema chiuso chiamato «ausiliario», che si sposta nello spazio per un certo
intervallo di tempo, che opera insieme al sistema aperto, il quale è fisso
nello spazio e nel tempo viene attraversato dal sistema chiuso ausiliario.
Chiariamo
il concetto appena espresso con questa equazione:
![]() (4)
(4)
dove è
espressa la massa del sistema aperto in una situazione all'istante ![]() , che in una fase successiva, trascorso il tempo
, che in una fase successiva, trascorso il tempo ![]() comporterà la
seguente:
comporterà la
seguente:
![]() (5)
(5)
Lezione del 29/11/2001 14:30-16:30
EQUAZIONE DI BILANCIO DELLA MASSA
Per
giungere al fine di trovare l'equazione di bilancio delle masse ricorriamo al
seguente esempio.
Consideriamo
il sistema fittizio qui sotto raffigurato in una situazione all'istante ![]() e l'altra all'istante
e l'altra all'istante
![]() . Il sistema chiuso ausiliario rappresentato, simbolicamente
con la linea blu, comprende il sistema aperto e una porzione di massa
. Il sistema chiuso ausiliario rappresentato, simbolicamente
con la linea blu, comprende il sistema aperto e una porzione di massa ![]() collocata nella
sezione d'ingresso del fluido,nel primo grafico, mentre la porzione di massa
nel secondo è collocata nella sezione di uscita del fluido. Quest'ultime non
sono relazionate tra di loro.
collocata nella
sezione d'ingresso del fluido,nel primo grafico, mentre la porzione di massa
nel secondo è collocata nella sezione di uscita del fluido. Quest'ultime non
sono relazionate tra di loro.
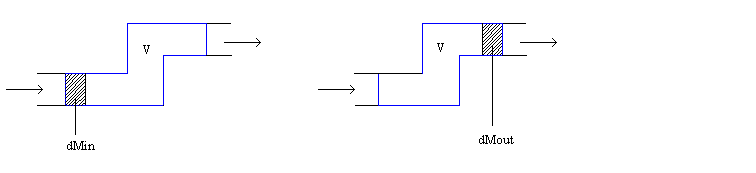 Dai seguenti schemi otteniamo l'uguaglianza:
Dai seguenti schemi otteniamo l'uguaglianza:
![]() (6)
(6)
in cui
nella prima troviamo la somma tra la massa della porzione entrante e la massa
nel sistema aperto V in relazione al
sistema chiuso ausiliario applicato nell'istante ![]() , mentre nel secondo la somma della porzione uscente e
l'energia interna in relazione al sistema chiuso nell'istante
, mentre nel secondo la somma della porzione uscente e
l'energia interna in relazione al sistema chiuso nell'istante ![]() .
.
Rapportando
l'intera equazione alla variazione di tempo otteniamo la seguente:
![]() (7)
(7)
supponendo
di sostituire il rapporto tra la porzione di massa entrante e la variazione di
tempo con la portata in massa all'entrata che incheremo con ![]() e naturalmente il rapporto tra la porzione di massa uscente e
la variazione di tempo con la portata
di massa all'uscita riconoscibile dal simbolo
e naturalmente il rapporto tra la porzione di massa uscente e
la variazione di tempo con la portata
di massa all'uscita riconoscibile dal simbolo ![]() .
.
Lezione del 29/11/2001 14:30-16:30
Ecco
allora come si presenta l'equazione aggiornata con le precedenti sostituzioni:
![]() (8)
(8)
dove
possiamo osservare che la variazione di massa contenuta in V è pari alla differenza
tra la massa entrata e quella uscita.
Se la
precedente equazione non presentasse la prima parte, ovvero la variazione di
massa contenuta in V, allora
parleremo di un equazione per un sistema stazionario. Per sistema stazionario
intendiamo un caso particolare di sistema chiuso, nel quale è presente una certa situazione di equilibrio tra massa
e lavori, (quindi parliamo di energia che non è detto che non possa entare ed
uscire).
Questo
equilibrio viene espresso così:
![]() (9)
(9)
e col
seguente esempio illustrato:
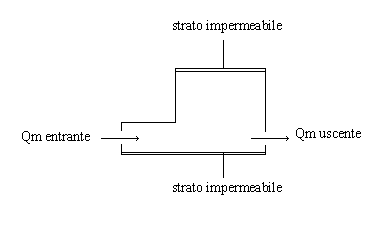
in cui
accertiamo quanto detto precedentemente:
![]() (10)
(10)
concludendo
quindi con la seguente formula:
![]() (11)
(11)
in cui
troviavo un'uguaglianza dei prodotti tra la densità, la velocità e la
superficie entranti e la densità , la velocità e la superficie uscenti.
Lezione del 29/11/2001 14:30-16:30
EQUAZIONE DI BILANCIO ENERGETICO
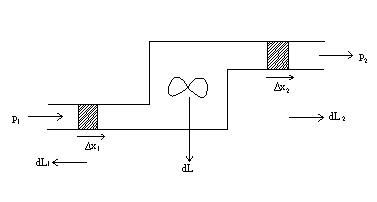
Lo schema sopra illustrato mi aiuta ad introdurre un nuovo argomento: l'utilizzo dell'equazione di bilancio energetico. Utilizziamo un sistema chiuso fittizio per ritrovare la soluzione nel sistema aperto. Come si può notare in esso avvengono scambi di calore ed energia.Gli scambi di lavoro avvengono tramite un dispositivo interno e tramite la variazione di volume, chetransita dall'entrata all'uscita.
![]() (12)
(12)
La
differenza tra l'energia totale con quella all'istante può essere uguagliata
alla differenza tra l'energia entrata sottoforma di calore e il lavoro:
![]() (13)
(13)
da cui
ricavo le seguenti:
![]() (14)
(14)
![]() (15)
(15)
da cui
posso anche togliere la seguente somma ![]() .
.
![]() (16)
(16)
Considerando
un sistema chiuso fittizio:
![]() (17)
(17)
Lezione del 29/11/2001 14:30-16:30
dove
sostituendo con le informazioni che ritroviamo nello schema sopra illustrato
ricaviamo:
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
dove ![]() rappresenta la potenza
termica scambiata,
rappresenta la potenza
termica scambiata, ![]() la potenza tecnica
scambiata e
la potenza tecnica
scambiata e ![]() l'intervallo di tempo
(il termine dell'energia potrebbe essere uguale a zero). Questa formula è ritrovabile in situazioni stazionarie
presenti in sistemi aperti con la caratteristica presenza di una sola entrata
ed una sola uscita. Ci troviamo davanti a una situazione equivalente a
l'intervallo di tempo
(il termine dell'energia potrebbe essere uguale a zero). Questa formula è ritrovabile in situazioni stazionarie
presenti in sistemi aperti con la caratteristica presenza di una sola entrata
ed una sola uscita. Ci troviamo davanti a una situazione equivalente a ![]() utilizzata per i
sistemi chiusi.
utilizzata per i
sistemi chiusi.
Ipotizzando
![]() e utilizzando
l'uguaglinza tra la differenza dell'entralpia uscente con quella entrante e la
differenza tra l'energia e il lavoro su unità di massa espressa con la seguente
e utilizzando
l'uguaglinza tra la differenza dell'entralpia uscente con quella entrante e la
differenza tra l'energia e il lavoro su unità di massa espressa con la seguente
![]() , ottengo:
, ottengo:
![]() (18)
(18)
dove
il simbolo «![]() » indica l'utilizzo delle grandezze fisiche Q ed L nell'unità di tempo.
» indica l'utilizzo delle grandezze fisiche Q ed L nell'unità di tempo.
L'unità
di misura sarà espressa in ![]() , ma più precisamente possiamo dimostrare come
, ma più precisamente possiamo dimostrare come ![]() possa essere definita
in unità di potenza:
possa essere definita
in unità di potenza:
![]()
![]() (19)
(19)
Lezione del 29/11/2001 14:30-16:30
Eserzio numero 1
Dati i seguenti: individuare:
![]()
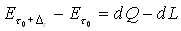
Per la
risoluzione di questo problema ricorriamo alla considerazione di un sistema chiuso
in quanto la massa del pistone è soggette a spostamento e ad un sistema aperto
nel caso consideri solo la camera d'aria.
Nel
passaggio dalla situazione iniziale a quella finale (![]() ) avviene che:
) avviene che:
![]()
![]()
Questo
esempio ci porta alla definizione di una trasformazione adiabatica in quanto
non è presente alcun scambio di calore:
![]()
![]()
![]()
![]()

Lezione del 29/11/2001 14:30-16:30
Possiamo
dare una rappresentazione grafica del passaggio da A a B caratterizzato da una
riduzione del volume e un aumento della pressione:

Abbiamo
quindi trovato la pressione all'interno della camera d'aria come richiesto dai
dati, per trovare la temperatura finale bisogna conoscere la mssa totale
essendo a conosenza del fatto che ![]() :
:
![]()
![]()
Se la
temperatura è richiesta in gradi centigradi è pari a ![]() .
.
L'ultimo
dato richiesto riguarda il lavoro necessario per gonfiare la camera d'aria:
![]()
![]()
Tenendo
conto della situazione ambientale:
![]()
![]()
Lezione del 29/11/2001 14:30-16:30
Esercizio numro 2
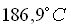
Il
problema ci pone davanti un sistema aperto provvisto di una compressione
adiabatica, molto veloce, dal quale entra aria a pressione ambientale che ad
una certa pressione esce.
![]()
ma
essendo una trasformazione adibatica, non esiste scambio di calore:
![]()
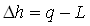
Nel grafico rappresentato lo spazio tratteggiato
rappresenta ilm lavoro tecnico presente nel sistema aperto.
![]()
![]()