Ponticelli Silvia
Matricola 138827
Lezione del 29/11/01 14.30-16.30
-SISTEMI APERTI E SISTEMI CHIUSI-
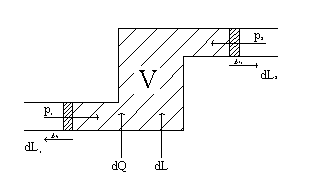
Def: si chiama SISTEMA CHIUSO un qualsiasi sistema, reale o fittizio, che non ha scambi di massa con l’esterno. Gli unici scambi permessi a questo tipo di sistema sono di calore Q e lavoro L, da cui la formula
![]() (1)
(1)
dove DU è
l’energia interna, rappresentante gli scambi energetici avvenuti:rappresenta
cioè lo stato di un sistema chiuso.

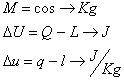 (2)
(2)
Def: si chiama SISTEMA APERTO un qualsiasi sistema la cui massa è soggetta a variazioni, così come il calore Q e il lavoro L. Ne rimane tuttavia inalterato il volume.
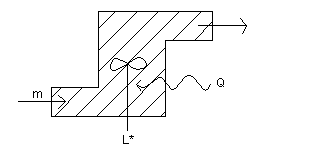
In questo tipo di sistema, m rappresenta la massa entrante e uscente e Q il calore entrante che, tramite un dispositivo, genera lavoro tecnico L*. Il lavoro tecnico è, infatti, definito come lo scambio di lavoro con dispositivi interni al sistema.
Lezione del 29/11/01-14.30-16.30
Considero ora un sistema chiuso fittizio:
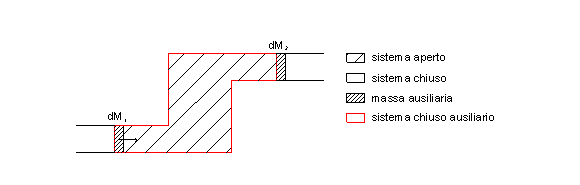 in cui
in cui ![]() rappresenta una
variazione di massa infinitesima:
rappresenta una
variazione di massa infinitesima: ![]() la massa entrante
e
la massa entrante
e ![]() la massa uscente. Non sono però relazionate in alcun
modo, infatti
la massa uscente. Non sono però relazionate in alcun
modo, infatti ![]()
![]() (3)
(3)
è
l’equazione che mi rappresenta la situazione iniziale del sistema aperto che
vado a studiare. ![]() è tutta la sua massa con l’aggiunta di quella ausiliaria
antecedente il sistema. In
è tutta la sua massa con l’aggiunta di quella ausiliaria
antecedente il sistema. In ![]() (l’istante di
partenza),
(l’istante di
partenza), ![]() entra nel sistema.
entra nel sistema.
![]() : in quest’intervallo, rappresentato dall’istante
: in quest’intervallo, rappresentato dall’istante ![]() a cui si aggiunge il
tempo
a cui si aggiunge il
tempo ![]() trascorso, la massa
trascorso, la massa
![]() entra nel
sistema ed esce dall’altra parte.
entra nel
sistema ed esce dall’altra parte.
L’equazione che per i sistemi chiusi è M=costante, si traduce, nei sistemi aperti, in questo modo:
![]() (4)
(4)
e descrive la massa contenuta nel sistema aperto V.
Dividendo
per ![]() , e operando con appositi passaggi, ottengo che la mia
equazione di partenza diventa:
, e operando con appositi passaggi, ottengo che la mia
equazione di partenza diventa:
![]() (5)
(5)
in
cui, in particolare, ![]() è la portata in massa
all’ingresso, e , al contrario,
è la portata in massa
all’ingresso, e , al contrario, ![]() la portata in massa
all’uscita.
la portata in massa
all’uscita.
Eguagliando
il primo membro a ![]() e il secondo a
e il secondo a![]() , ottengo:
, ottengo:
![]() (6)
(6)
che mi dice che la variazione di massa all’interno del sistema aperto V è pari alla differenza tra la massa entrata e quella uscita.
Lezione del 29/11/01-14.30-16.30
-SITUAZIONE DI EQUILIBRIO-
Una situazione di equilibrio all’interno di un sistema aperto, presuppone che si sia bloccata la situazione di massa totale e di energia dentro il sistema (nonostante ciò è consentito passaggio di massa).
Tradotto in un’equazione si ha:
![]() (7)
(7)

(il sistema è studiato nel caso abbia una sola entrata e una sola uscita)
Considerando:
![]() densità all’ingresso e
densità all’ingresso e ![]() densità all’uscita
densità all’uscita
![]() velocità all’ingresso e
velocità all’ingresso e ![]() velocità all’uscita
velocità all’uscita
![]() superficie all’ingresso e
superficie all’ingresso e ![]() superficie all’uscita
superficie all’uscita
Si ha che:
![]() (8)
(8)
-EQUAZIONE DEL BILANCIO ENERGETICO-
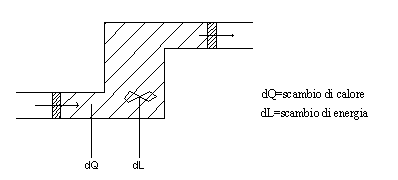
Considero un sistema chiuso fittizio, il suo bilancio energetico sarà:
Lezione del 29/11/01-14.30-16.30
![]() (9)
(9)
(si
noti l’uguaglianza con i sistemi chiusi, in cui ![]() ), l’energia totale del sistema sarà quindi data dall’energia
di V, più l’energia
), l’energia totale del sistema sarà quindi data dall’energia
di V, più l’energia ![]()
![]() (10)
(10)
in cui
![]() rappresenta l’Energia
totale ed
rappresenta l’Energia
totale ed ![]() l’energia iniziale.
l’energia iniziale.
Svolgendo l’equazione del bilancio energetico, precedente, si ha che l’energia totale sarà:
![]() (11)
(11)
in cui
![]() pressione,
pressione, ![]() energia cinetica, ma si possono trascurare,
energia cinetica, ma si possono trascurare, ![]() è, invece, l’energia
contenuta in V, all’istante
è, invece, l’energia
contenuta in V, all’istante ![]() .
.
L’energia iniziale sarà:
![]() (12)
(12)
![]() (13)
(13)
in cui
![]() è il lavoro scambiato
dalle due superfici mobili
è il lavoro scambiato
dalle due superfici mobili ![]() e
e ![]() ,
,
![]() e
e ![]() (14)
(14)
![]() (15)
(15)
Lezione del 29/11/01-14.30-16.30
Per cui, il lavoro tecnico ottenuto in funzione della precedente formula sarà:
![]() (16)
(16)
![]() (17)
(17)
dividendo
per h ottengo l’equazione che mi
descrive la variazione di energia continua in V, nel tempo ![]() .
.
![]() (18)
(18)
dove ![]() rappresenta la
potenza termica,
rappresenta la
potenza termica, ![]() la potenza tecnica, e
la potenza tecnica, e
![]() l’intervallo di tempo
(questa formula è valida in situazioni di sistemi stazionari aperti con una
sola entrata e una sola uscita).
l’intervallo di tempo
(questa formula è valida in situazioni di sistemi stazionari aperti con una
sola entrata e una sola uscita).
Ponendo
![]() e moltiplicando
nell’equazione precedente, ottengo:
e moltiplicando
nell’equazione precedente, ottengo:
![]()
![]() (19)
(19)
in cui ![]() e
e ![]() rappresentano
rispettivamente il calore totale e la potenza tecnica dati nell’unità di tempo,
rappresentano
rispettivamente il calore totale e la potenza tecnica dati nell’unità di tempo,
![]() l’energia specifica
entrante, ed
l’energia specifica
entrante, ed ![]() l’energia specifica
uscente. E si può considerare come la semplificazione dell’equazione:
l’energia specifica
uscente. E si può considerare come la semplificazione dell’equazione:
![]()
![]() (20)
(20)
[WATT:
unità di misura della potenza, il simbolo ![]() sta ad indicare che
l’unità di misura che sto trattando è considerata nel tempo: quantità/tempo].
sta ad indicare che
l’unità di misura che sto trattando è considerata nel tempo: quantità/tempo].
Lezione del 29/11/01-14.30-16.30
ESERCIZI
N°1

DATI INCOGNITE
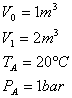
![]()
[posso considerare il sistema come se fosse chiuso]
(stato
iniziale) ![]() (Dopo la traslazione del pistone
da A a B).
(Dopo la traslazione del pistone
da A a B).
(stato
finale) ![]()
![]()
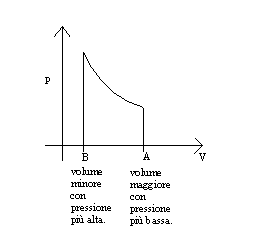

![]() [
[![]() dell’aria
dell’aria![]() ]
]
Lezione del 29/11/01-14.30-16.30
-Pressione Finale:
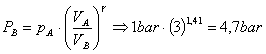 [circa 5 volte la
pressione ambientale]
[circa 5 volte la
pressione ambientale]
-Massa Totale:
![]() [
[![]() ]
]
-Temperatura Finale:
![]()
![]()
Ricordiamo che ![]() , ma in questo caso, essendo una trasformazione adiabatica
reversibile, posso eliminare il calore Q.
Mi resta da trovare il lavoro L.
, ma in questo caso, essendo una trasformazione adiabatica
reversibile, posso eliminare il calore Q.
Mi resta da trovare il lavoro L.
![]()
![]()
L’equazione rappresenta il lavoro totale (cui contribuisce la pressione atmosferica), vale a dire il lavoro dato dall’esterno per fare questo tipo di compressione. Il segno negativo è una convenzione che sta ad indicare il lavoro esterno.

In particolare, la parte del lavoro totale fornita dalla pressione atmosferica esterna, è data dalla formula:
![]()
Il lavoro netto, invece, è:
![]()
![]()
Lezione del 29/11/01-14.30-16.30
N°2
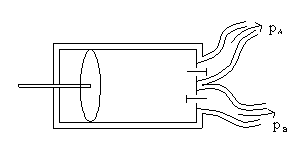
(questo sistema va considerato aperto, poiché ha due aperture che consentono scambio di materia con l’esterno).
![]() (
(![]() in quanto si tratta di una trasformazione adiabatica)
in quanto si tratta di una trasformazione adiabatica)
![]()
dove ![]() e
e ![]() rappresentano,
rispettivamente, la temperatura d’uscita e la temperatura d’entrata.
rappresentano,
rispettivamente, la temperatura d’uscita e la temperatura d’entrata.
Svolgendo l’equazione ottengo -L, il lavoro tecnico che occorre per comprimere il fluido.
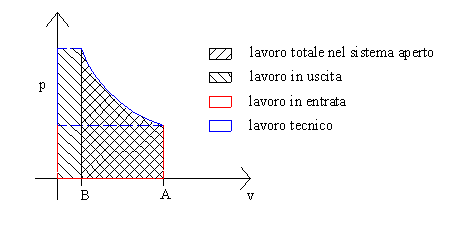
Nel sistema aperto interessa solo il lavoro tecnico:
![]()
![]()