Zanettini Viola,
matricola 134275, lezione 11-01-2001, ore10.30-12.30
ESERCIZIO
Determinare il dimensionamento di una pompa che eroga acqua in un autoclave. Il gas presente nell’autoclave è compresso in modo che l’acqua vi affluisca in pressione maggiore di quella atmosferica.
L’autoclave è utile in casi di emergenza, come ad
esempio per spegnere incendi; infatti il fluido esce spontaneamente senza
bisogno di corrente elettrica.
Questo dispositivo però viene comunemente usato per impianti di riscaldamento, in particolare per edifici di altezza superiore a 30 metri. Infatti, in un circuito chiuso, come può esserlo quello di un impianto di riscaldamento condominiale, con l'aumentare della temperatura, il volume dell'acqua diminuisce (e di conseguenza anche la pressione dell'aria);dunque non sarebbe sufficiente la sola forza di una pompa.Si correrebbe così il rischio di non riuscire a rifornire i piani più alti di acqua calda. Ora, essendo stata dimensionata per mantenere costante la pressione dell'aria nel secondo serbatoio, l'autoclave appena nota una diminuzione di quest'ultima, aziona la pompa e ristabilisce così il volume di acqua e la pressione iniziale.
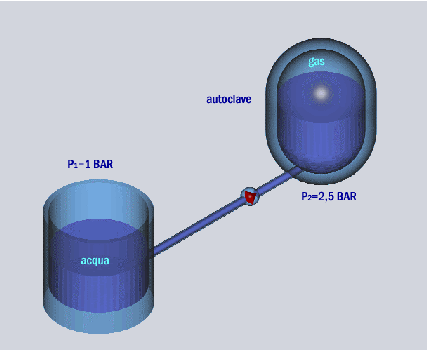
Il gas nell’ autoclave ha una pressione P2= 2,5 BAR
Il fluido deve affluire attraverso il tubo con una portata
di
![]() = 3 Kg/s (*)
= 3 Kg/s (*)
Dove
ricordiamo che la portata in massa è la quantità d’acqua che attraversa la
superficie ![]() nel tempo
nel tempo![]()
Il tubo ha una sezione D = 0,05 m
e una lunghezza L = 8 m
Data la
lunghezza del tubo bisogna considerare tutte le fonti di perdita di carico. Il
tubo è d’acciaio, con scabrezza relativa: ![]()
I tubi più lisci
sono quelli in acciaio inox, in plastica…
La portata dovrà essere di almeno 1,5 BAR per poter vincere la differenza di pressione; in realtà sarà ancora maggiore perché bisogna considerare le perdite di carico R accidentali.
Equazione di Bernoulli:
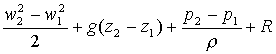
![]()
La scelta delle sezioni non è banale. Per comodità sceglieremo le sezioni ai peli liberi, in quanto essendo le più vaste la velocità è trascurabile. In questo modo possiamo eliminare il primo termine dell’equazione e riscriverla tenendo conto che l’acqua è un fluido incomprimibile.
Anche
il dislivello è nullo quindi possiamo eliminare anche il secondo termine.


![]()
![]()
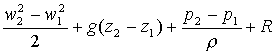
![]()
Rimane che:
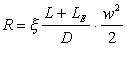
Dove LE = accidentalità di sbocco ( LE1) e di imbocco(LE2)
Ricaviamo ora il Numero di Reynolds:
![]() dove
dove ![]() = viscosità cinematica
= viscosità cinematica ![]()
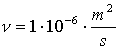
Sapendo che
la portata è ![]() =
=![]() ricaviamo la velocità
ricaviamo la velocità
![]()
L’area della
sezione del tubo è 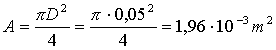
Sostituendo trovo la velocità
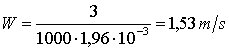
Possiamo allora ricavare il Numero di Reynolds
![]()
Se il numero
di Reynolds è maggiore di 2300, allora il moto è turbolento, se è
inferiore è laminare. Nel nostro caso il numero trovato è maggiore del
valore limite 2300, quindi il moto è turbolento. Passiamo ora alla valutazione del
fattore accidentalità che in questo caso, ricordiamo, non è banale, in quanto
il fattore di attrito ξ è funzione del Numero di Reynolds
ξ = ![]() . Per fare ciò dobbiamo controllare sul diagramma di Moody.
. Per fare ciò dobbiamo controllare sul diagramma di Moody.
DIAGRAMMA DI MOODY
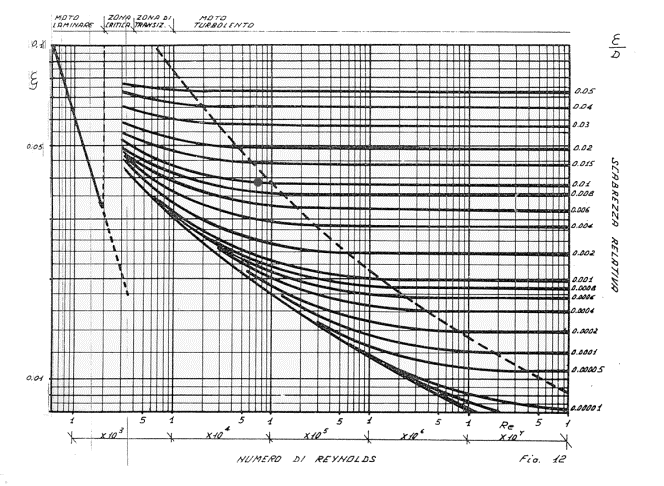
In ascissa abbiamo il numero di Reynolds in scala logaritmica.
In ordinata la scabrezza relativa.
Stimiamo
0,0385 il valore del coefficiente di attrito ![]() .
.
Ora bisogna valutare le lunghezze equivalenti utilizzando il Nomogramma:
Lunghezza equivalente
di sbocco ![]()
Lunghezza
equivalente di imbocco ![]()
NOMOGRAMMA

Collegando l’ordinata del diametro interno 50 mm con il valore delle accidentalità di imbocco (14) e di allargamento di sezione (10) dell’ordinata di sinistra trovo rispettivamente i valori delle lunghezze equivalenti.
![]()
Possiamo ora calcolare le perdite di carico totali:
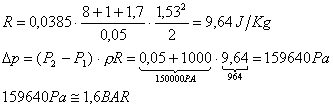
Si può osservare che quasi tutta l’energia elettrica è stata convertita in energia meccanica dall’autoclave;questo perché l’acqua è un fluido poco viscoso e il diametro del tubo è molto piccolo.
ESERCIZIO
Dato un serbatoio pieno d’acqua collegato ad un tubo, che ipotizziamo liscio, dobbiamo calcolare quanto tempo viene impiegato perché il serbatoio si svuoti.
Sappiamo che:
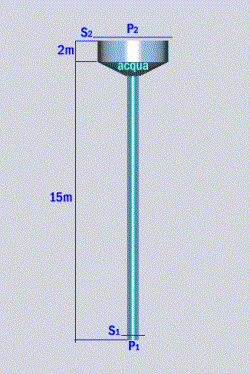
Ltot =17 m
D = 0,1 m
![]()
Essendo il
dislivello medio ![]() ,quindi non trascurabile, la velocità del fluido non sarà
costante.
,quindi non trascurabile, la velocità del fluido non sarà
costante.
Dalla portata in volume (dove il volume del serbatoio è espresso in funzione del tempo) ricavo che:
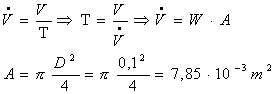
Possiamo vedere che la vera incognita è la velocità e per determinarla ricorro all’equazione di Bernoulli.
![]()
![]()
![]()
![]()
![]()
Importante è la scelta delle sezioni:
S1= pelo libero (dove la velocità è nulla)
S2= sbocco (dove la velocità non è trascurabile)
![]()
Nel nostro caso la differenza di quota è negativa perché la seconda quota è posta più in basso della prima quota. Anche il termine delle pressioni sparisce in quanto la P1 coincide con la pressione atmosferica, e, contrariamente alla nostra percezione, anche la P2 ha la stessa pressione dell’aria. La pressione che avvertiamo aprendo un rubinetto in realtà è la quantità di moto causata dalla velocità.
Avendo uguale pressione P1 e P2 posso eliminarle dall’equazione.
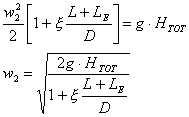
se il fluido
è inviscido e i fenomeni di attrito trascurabili: ![]()
![]() Velocità
Torricelliana (rappresenta un corpo lasciato cadere con moto uniformemente
accelerato, quindi se non ci fossero fenomeni di attrito il corpo
raggiungerebbe la stessa velocità di un grave lasciato cadere; ma i fluidi sono
viscosi e presentano fenomeni dissipativi che rendono la loro velocità più
bassa)
Velocità
Torricelliana (rappresenta un corpo lasciato cadere con moto uniformemente
accelerato, quindi se non ci fossero fenomeni di attrito il corpo
raggiungerebbe la stessa velocità di un grave lasciato cadere; ma i fluidi sono
viscosi e presentano fenomeni dissipativi che rendono la loro velocità più
bassa)
Il fattore di
attrito è funzione del numero di Reynolds e della scabrezza relativa ![]()
Conoscendo la scabrezza relativa devo determinare il numero di Reynolds
![]()
Dobbiamo abbozzare un ipotetico valore della velocità. Dato che la velocità di Torricelli costituisce il tetto limite, prendiamo la sua metà:
![]()
Probabilmente
il valore scelto è sbagliato, ma dopo alcuni loop i valori si uniformeranno. ![]()
Questo valore è molto alto, ma controllo lo stesso il fattore d’attrito.
Mi riferisco ora al DIAGRAMMA DI MOODY
Il fattore di
attrito risulta:![]()
Calcolo la nuova velocità tenendo presente che in questo caso i fenomeni di attrito non sono trascurabili. Cerco prima la lunghezza equivalente sul Nomogramma:
LE = 2,1
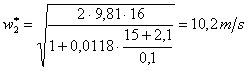
Facciamo ora un secondo “giro”: calcolo un nuovo valore di Reynolds
![]()
Sul diagramma di Moody trovo una nuova stima del fattore di attrito:
![]()
Ricavo un nuovo valore della velocità:
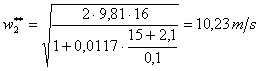
Posso a questo punto fermarmi perché i valori sono pressoché uniformi.
Trovo allora la portata in volume:
![]()
![]()
Il tempo impiegato perché il serbatoio si svuoti è poco più di un minuto. Se voglio che si svuoti più rapidamente devo allungare il tubo affinché le lunghezze equivalenti risultino nulle.
ESERCIZIO
Dimensionare la tubazione collegata ad un serbatoio contenente acqua.
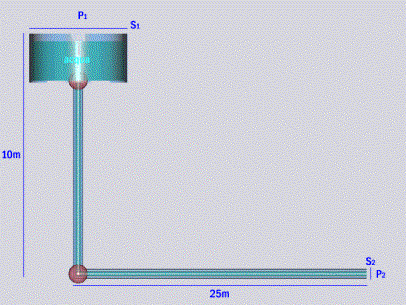
Fluido: acqua
Portata in
massa: ![]()
TABELLA DEI DIAMETRI NORMALIZZATI DEI TUBI
ISO 7/1 - UNI 338 - BS 21 - DIN 2999.
|
Diametro nominale G |
Diametro esterno filettatura |
PASSO |
Altezza filetto |
Lunghezza utile filettatura cilindrica |
|
|
N° fil/1" |
mm |
||||
|
3/8" |
16,66 |
19 |
1,337 |
0,857 |
11,4 |
|
½" |
20,95 |
14 |
1,814 |
1,162 |
15,0 |
|
3/4" |
26,44 |
14 |
1,814 |
1,162 |
16,3 |
|
1" |
33,25 |
11 |
2,309 |
1,479 |
19,1 |
|
1¼" |
41,91 |
11 |
2,309 |
1,479 |
21,4 |
|
1½" |
47,80 |
11 |
2,309 |
1,479 |
21,4 |
|
2" |
59,61 |
11 |
2,309 |
1,479 |
25,7 |
|
2¼" |
65,71 |
11 |
2,309 |
1,479 |
- |
|
2½" |
75,18 |
11 |
2,309 |
1,479 |
30,2 |
|
2 ¾" |
81,53 |
11 |
2,309 |
1,479 |
- |
|
3" |
87,88 |
11 |
2,309 |
1,479 |
33,3 |
|
4" |
113,03 |
11 |
2,309 |
1,479 |
39,3 |
|
5" |
138,43 |
11 |
2,309 |
1,479 |
43,6 |
|
6" |
163,83 |
11 |
2,309 |
1,479 |
43,6 |
Bisogna procedere per tentativi: considero primamente un diametro di 1 pollice
![]()
Ricavo l’area del diametro del tubo di passaggio:
![]()
Ricavo la velocità del fluido nell’attraversare l’area A:
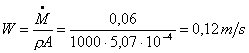
Ricorro all’equazione di Bernoulli:
![]()
![]()
![]()
![]()
Posso eliminare primamente la velocità dell’acqua al pelo libero dacché è pressoché nulla, nonché la differenza di pressione che, per i motivi esposti nell’esercizio precedente, è inesistente.
Passo ora alla scelta astuta delle sezioni:
S1 = al pelo libero
S2 = allo sbocco
L’equazione di Bernoulli diventa dunque:
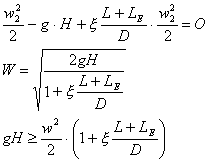
Controllo ora
il fattore di attrito ![]() nel diagramma di
Moody e le lunghezze equivalenti nel Nomogramma:
nel diagramma di
Moody e le lunghezze equivalenti nel Nomogramma:
![]()
Valore che supera di poco il limite tra moto turbolento e laminare.
![]()
Cerco ora le lunghezze equivalenti:
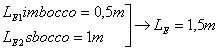
Sostituisco nell’equazione di Bernoulli:
![]()
![]()
La disequazione è verificata ma il tubo è troppo grosso; considereremo il valore esatto e l’esercizio risolto solo quando il rapporto tra le velocità sarà di 2,3 o massimo 5. In altre parole i due termini della disuguaglianza devono approssimarsi.
Scelgo un
nuovo valore di diametro: ![]()
Calcolo la
nuova area di sezione:![]()
Calcolo la
nuova velocità: ![]()
Il nuovo
valore di Reynolds: ![]() (moto turbolento)
(moto turbolento)
Guardo il
diagramma di Moody e trovo un coefficiente di attrito: ![]() ,quindi posso considerare il tubo liscio.
,quindi posso considerare il tubo liscio.
Riscrivo ora la disuguaglianza:
![]()
![]()
Il rapporto è
ancora troppo grande: ![]()
Scelgo un
diametro più piccolo: ![]() Il valore più
piccolo trovato
Il valore più
piccolo trovato
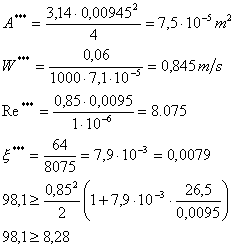
Ma il
rapporto è ancora troppo grande:![]()
Probabilmente
se il rapporto deve essere almeno 5, il diametro sarà ![]() circa, ovvero
circa, ovvero ![]() !!
!!