STEFANO MOFFA
133647
21/12/2000 ore 16.30 - 18.30
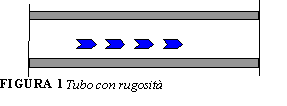
Perdite di carico DISTRIBUITE
Indichiamo con R le perdite di carico; R si divide in:

Le prime sono dovute a rugosità o irregolarità della superficie del tubo. All’aumentare della lunghezza dell’impianto, R aumenta.
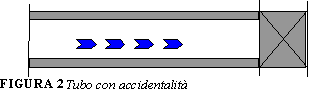
Le seconde si hanno quando nell’impianto si incontrano valvole, rubinetti, curve, ecc. In questo caso la perdita è concentrata per esempio in una curva.
La perdita di carico è un calo di pressione e per calcolarla si può utilizzare l’equazione che esprime la velocità in funzione della variazione di pressione.

![]()
se si considera il raggio del tubo
![]()
se si considera il diametro.
Dove (w) indica la velocità media
(L) la lunghezza del tubo
(m ) la viscosità (tabulata).
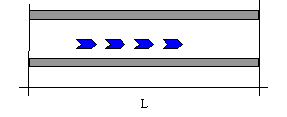
La perdita di carico è quindi direttamente proporzionale alla viscosità e alla velocità del fluido e alla lunghezza del tubo ed è inversamente proporzionale al quadrato del raggio della sezione. Ad ogni metro di tubo corrisponde quindi una certa perdita di carico; inoltre, più il fluido scorre veloce, più energia viene dissipata.
Dato che le perdite di carico risultano proporzionali alla lunghezza del condotto, si considerano distribuite lungo il condotto stesso e per questo vengono definite perdite distribuite.
Possiamo esprimere D p in funzione del numero di Reynolds.
Nel caso di condotte a sezione circolare:
![]()
dove
![]()
è definito il fattore di attrito di condotte circolari.
Nel caso di condotte non circolari si usa la formula più generale:
![]()
Il fattore di attrito varia a seconda della forma della sezione del tubo. Esso varia anche a seconda della lavorazione del tubo: queste formule valgono per tubi lisci; se il tubo non fosse liscio anche le asperità della sua superficie contribuirebbero alle perdite di carico.
Se non conosco x utilizzo il diagramma di Moody, dove ε indica l’altezza media delle asperità e d indica il diametro del tubo.
Introduco il valore ε/d di scabrezza relativa e per ognuno di questi ho una curva sul grafico.
Conosco anche Re, dunque una volta individuata l’intersezione delle due curve vado a leggere il valore di ξ corrispondente sull’asse delle ascisse.
Esercizio:
T = -12,2°C
w = 21,3 m/s
D = 50,8 mm
L = 22,86 m
ε = 0,046 mm
(rugosità della superficie)μ = 8,
6·10-6 Pa·sUsiamo la formula più generica, perché anche se la condotta è circolare, devo considerare la rugosità della superficie.
Per prima cosa calcolo Re:
![]()
(Moto fortemente turbolento).
![]()
![]()
Quindi possiamo dire che il fattore di attrito dipende prevalentemente da due fattori:
I valori del fattore di attrito ξ sono rappresentati tramite un diagramma, realizzato tramite scala doppio logaritmica, le cui ascisse riportano il numero di Reynolds Re e le ordinate il fattore di attrito ξ.
Il diagramma si divide in tre zone distinte:

FIGURA 4
Diagramma di MoodyBisogna ricordare che il fattore di attrito è noto solo se è noto il numero di Reynolds.
Causa di caduta di pressione nei condotti idraulici sono anche le perdite di carico concentrate o localizzate, esse sono dovute ad ostacoli come, ad esempio, curve, gomiti, valvole, brusche variazioni di pressione che il fluido può incontrare mentre scorre all’interno del tubo, restringimenti bruschi del tubo.
Si può scrivere quindi che:
R à Δp = Δperdite distribuite + Δperdite concentrate
La formula delle perdite di carico concentrate è simile a quella delle perdite di carico distribuite, ma a differenza di queste ultime non dipendono dalla lunghezza del tubo (scompare il termine L/D), in quanto sono localizzate in un punto preciso. Quindi se indichiamo con β il fattore di attrito, l’espressione assume la forma:
![]()
in cui w e ρ sono rispettivamente la velocità media e la densità del fluido. Bisogna notare però che se il diametro del tubo è costante, anche la velocità rimane costante; se però il diametro varia la velocità in uscita sarà diversa dalla velocità in entrata. Infatti se la sezione si allarga la velocità diminuisce, viceversa se il diametro del tubo diminuisce, la velocità aumenta. Questo vale però se la densità del fluido ρ rimane costante, poiché al variare della pressione potrebbe variare anche il volume specifico del fluido e quindi anche la sua densità. Può essere quindi ragionevole considerare ρ costante.
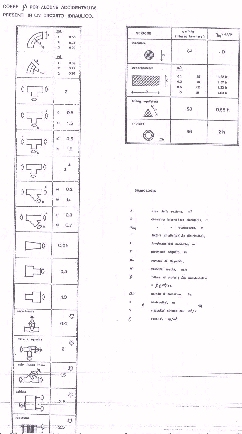
FIGURA 5
Coeff. β per alcune accidentalità
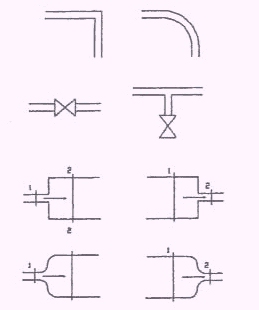
FIGURA 6
Alcuni esempi diperdite di carico concentrate
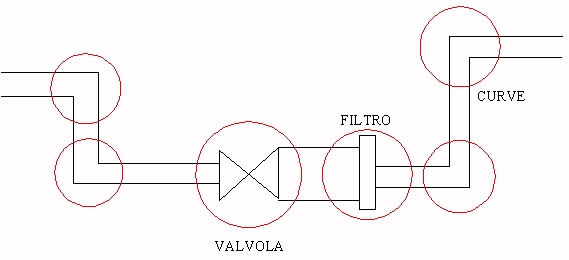
FIGURA 7
Esempio di sistema con 6 perdite di carico
In un sistema con n perdite di carico concentrate, la perdita di carico totale sarà la somma delle singole perdite:
![]()
![]()
Per passare dalla prima alla seconda formula esiste una tabella (nomogramma), che ha tre colonne:
Se conosco due punti, che stanno sulle due colonne esterne, e li unisco, intercetto su quella centrale la lunghezza equivalente che mi da una stessa perdita di carico.
Per calcolare la perdita di carico totale, anziché sommare alle perdite di carico distribuite le perdite di carico concentrate, esiste un metodo alternativo, il quale consiste nell’utilizzare direttamente la formula delle perdite di carico, con la sola accortezza di maggiorare la lunghezza del condotto sostituendo L con L+LEQ, dove LEQ è la somma delle lunghezze equivalenti di tutte le accidentalità.
Per determinare una lunghezza equivalente si usa il seguente nomogramma:

FIGURA 8
NomogrammaSulla colonna di destra sono riportati i valori del diametro interno della sezione del tubo in millimetri, su quella di sinistra i valori corrispondenti delle accidentalità del tubo e su quella centrale i valori della lunghezza equivalente in metri. Quindi se si conosce il diametro interno del tubo e il tipo di accidentalità si può ricavare il valore della lunghezza equivalente semplicemente congiungendo con una retta i due punti sulle colonne esterne corrispondenti ai valori noti: la lunghezza equivalente è pari al valore in metri corrispondente al punto in cui tale retta interseca l’asse centrale.
Esercizio
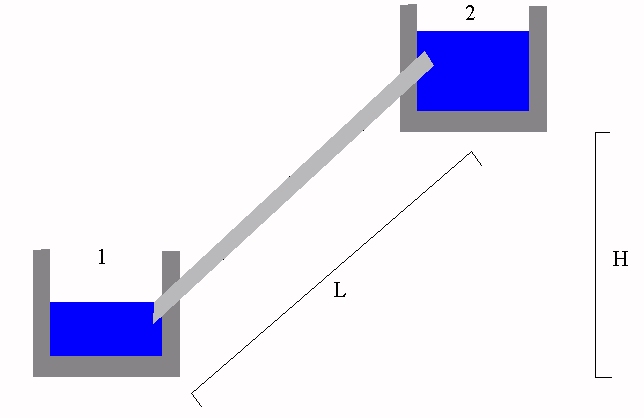
H = 50 m
D = 100 mm
L = 1 km
V = 20 l/s (portata) nel tubo passano 20 litri al secondo
ρ = 920 kg/m
3μ = 8,5 Poise
ε/D = 0 (tubo liscio)
Utilizzo l’equazione di Bernoulli:
![]()
![]()
V = w·A (dove A indica la sezione del tubo)
![]()
Devo calcolare la perdita di carico distribuita R, tenendo conto che la superficie non è scabra.
![]()
![]()
![]()
![]()
I tre termini sommati corrispondono a:
energia CINETICA + energia POTENZIALE + PERDITE DI CARICO
Nel bilancio la perdita di carico ha perso maggiore: la caduta di pressione è dovuta quasi interamente ad essa, mentre il primo termine è trascurabile.