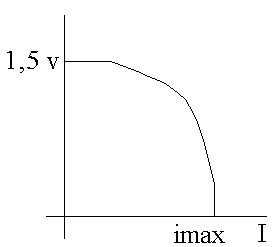
Filippini marco - matr.133583 - Lezione del 12/01/01 - ora 8:30-10:30
Moto dei fluidi
Nel moto dei fluidi si hanno due categorie:
L'idraulica studia le leggi dell'equilibrio e del moto dei liquidi in genere, dell'acqua in particolare, con la stessa densità. L'equazione di Bernoulli ci permette di calcolare la prevalenza, in una condizione di moto a volume costante.
W2²-W1² / 2 + g(Z2-Z1) + P1-P2 / ρ + R = -l = Δp / ρ
(1)
Con essa possiamo esprimere la prestazione della pompa come salto di pressione tra l'ingresso e l'uscita. Chiaramente esiste un rapporto tra la prevalenza della pompa e la propria portata.
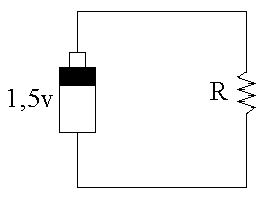
Per esemplificare il rapporto tra la prevalenza, o prestazione, della pompa e la portata, in fig.(1) è rappresento un circuito con una pila ed una resistenza e nel grafico a fianco è rappresentata la corrente massima (imax) che la pila può erogare.
fig.(1)
Quindi nel caso della pompa fig.(2) la curva caratteristica è uguale alla precedente e rappresenta la massa circolante massima, inoltre la potenza erogatrice è direttamente proporzionale alla dimensione fisica della macchina.
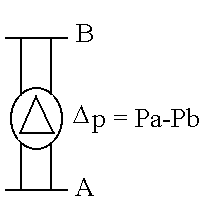
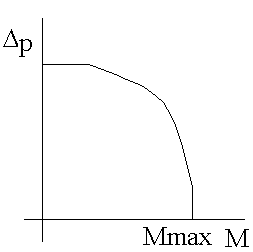
fig.(2)
Esempio:
In un aula dal volume V = 1000 m³ deve essere cambiata l'aria interna due volte all'ora. Quindi la portata della nostra pompa dovrà essere di 2000 m³/h. E' necessario dimensionare la portata in massa della pompa.
V = 2 ricambi/h
V = 2000 m³/h
V = 1/ρ = V/M = R·T / P = 0,87 m³/Kg {volume specifico dell'aria}
M =V · 1/v = V·ρ = 2000·1,18 = 2360 Kg/h = 0,65 Kg/s

fig.(3)
In fig.(3) è rappresentato il grafico in cui sono indicati i valori progettuali di Δp e Mp, che servono a dimensionare la pompa. E' necessario tenere un margine di sicurezza rispetto ai calcoli puri, per cui si deve introdurre un coefficiente di sicurezza che vada ad incrementare le prestazioni necessarie della pompa.
La portata è un dato essenziale perché ci permette di stabilire la potenza della pompa che dovremo utilizzare, ma questa portata che avremo calcolato non dovrà mai essere quella massima della pompa. E' necessario che la prevalenza a vuoto sia di qualche bar in più perché:
Problema del tiraggio dei camini
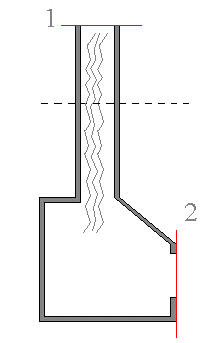
fig.(4)
Il problema del tiraggio di camini è un caso particolare, infatti apparentemente sembrerebbe un moto a densità variabile visto che la densità esterna dell'aria è diversa da quella interna dei fumi, ma è da considerarsi la coppia di sezioni 1 e 2 tra cui la densità non varia.
ρF < ρA
Accesa la fiamma i fumi salgono ed escono, il moto che si crea all'interno alla cappa è isotermico. Poiché non ci sono grandi differenze di altezza e di pressione i fumi salgono perché la loro densità è minore della densità dell'aria fuori.
Esercizio:
Dimensionare una pompa che deve collegare due serbatoi. Il fluido contenuto nei due serbatoi è olio per motori d'aereo.
H = Z2-Z1 = 50 m {differenza di quota a peli dell'acqua}
ρ = 0,92 gr/m³ = 920 Kg/m³
d =100 mm = 0,1 m {tubo circolare}
L = 1 Km = 1000 m
μ {coeff. di viscosità o viscosità dinamica} = 8,5 Poise→8,5·10ˉ5 Ns/m²
V = 20 l/s
Δp = ? P = ?
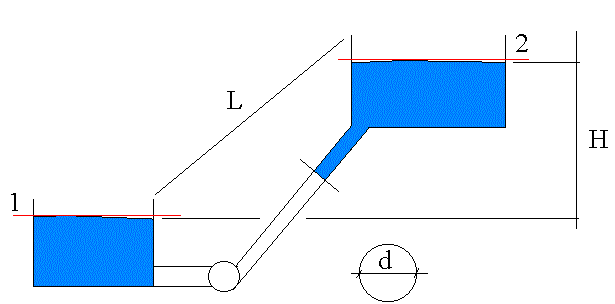
fig.(5)
In questo caso la coppia di sezioni 1 e 2 verrà presa ai peli dell'acqua per favorire il procedimento durante la risoluzione del problema.
Iniziamo considerando l'equazione di Bernoulli (1):
W2²-W1² / 2 + g(Z2-Z1) + P1-P2 / ρ + R = -l = Δp / ρ
Dall'equazione si nota che essendo la differenza di velocità, al pelo dell'acqua, costante e la differenza di pressione, essendoci solamente un dislivello di 50m, pari a 0, l'equazione viene semplificata.
g(Z2-Z1) + R = -l = Δp / ρ
A questo punto dovremo solamente andare a calcolare le perdite di carico (R). Essendo le perdite di carico distribuite maggiori di quelle concentrate queste ultime sono sottovalutabili.
R = Rd + Rc → (Rd > Rc) = ξ L/D · W²/2
(2)
Sapendo che il fattore d'attrito ξ è funzione del numero di Reinolds dovremo prima calcolare esso.
ξ(Re) → Re = W·D/μ
(3)
Non conoscendo la velocità con cui il fluido scorre nel tubo (W) dovremo calcolarla, conoscendo il diametro del tubo (D), quindi l'area, e la portata (V).
A
= π D²/4 = 3,14 · 0,1²/4 = 7,85·10ˉ³ m²
V = W·A
(4)
W = V/A = 20·10ˉ³ / 7,85·10ˉ³ = 2,55 m/s
Re = W·D/μ = 2,55·0,1/8,5·10ֿ5 = 276 ← laminare
Il moto del fluido è laminare, quindi riconducibile ad una retta, perché sappiamo, dal diagramma di Moody, che se il numero di Reinolds è inferiore a 2300 il moto è laminare altrimenti superiore a 4100 è turbolento.
A questo punto procediamo con il diagramma di Moody, ricavando ξ
ξ
= 64/Re
ξ = 64/276 = 0,232
Ora andremo a ricavare le perdite di carico (R) utilizzando i dati ricavati.
R = 0,232 · 1000/0,1 · 2,55²/2 = 7539 J/Kg
Δp = ρ·l =920·8030 = 7˙387˙600 Pa = 73,9 BAR
Abbiamo cosi ricavato la prevalenza (Δp), cioè la caduta di pressione che deve fornire la pompa per far scorrere il fluido da un serbatoio all'altro, ora dovremo andare a dimensionare la potenza.
M
= ρ · V = ρ · W · A = 920 · 20·10ˉ³ = 18,4 Kg/s
P = 8030 · 18,4 = 147˙752 W = 147 Kw
η
{rendimento} = 0,70 = Pout/Pin
Pin = Pout/η =147/0,7 = 211˙074 W = 211 Kw