Esercizi di riepilogo in preparazione all’esame

 

Il moto esterno è una parte della fluidodinamica che studia il moto dei fluidi attorno ai corpi in modo indifferente sia nel caso in cui l’oggetto sia fermo e il fluido si muova che viceversa.

Problemi tipici sullo studio del moto esterno possono riguardare:

- il dimensionamento di tralicci, affinché possano sopportare le forze che il vento esercita su di essi;

-il calcolo della velocità di caduta di un oggetto all’interno di un fluido.

 

Esercizio 1

Determinare lo sforzo risultante esercitato dal vento sulla base di un camino, sapendo che quest’ultimo è investito perpendicolarmente dal vento, il quale soffia a una velocità di 100 km/h.

Sarà doveroso da parte del “bravo architetto” dimensionare la fondazione, affinché sopporti le tre forze che agiscono su di essa, quali la forza peso, la forza di trascinamento e la forza di rotazione.

 

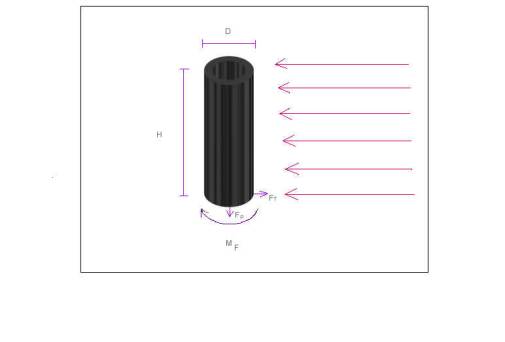
H = altezza del camino = 15 m

D = diametro del camino = 1 m

u¥ = velocità del vento = 100 km/h

FT = forza di trascinamento = ?

MF = momento flettente = ?

 

Trovata la velocità del vento in m/s come è espressa nel Sistema internazionale (S.I.) :

u¥ = 100*1000/3600 = 27,8 m/s

si ricava, ricordando la legge di Bernoulli, che la forza di trascinamento è uguale a:

FT = CR*1/2*u2¥*rARIA*AF  (la formula è stata adattata ai nostri dati)

 

Nota :

-FT rappresenta la forza applicata nel centro di spinta, posto nel baricentro ( punto in cui può pensarsi applicato il peso del corpo; in tutti i corpi aventi un centro di simmetria il baricentro coincide con esso ) del cilindro a una distanza H/2 dal suolo.

-CR rappresenta il coefficiente di resistenza e determina la forza di attrito, che si oppone al moto relativo del fluido/oggetto; tale forza è anche detta forza resistente. Il CR dipende dalla scabrezza del corpo e dal numero di Reynolds (Re) .

-u¥ rappresenta la velocità del fluido che scorre con un profilo di velocità piatto.

-rARIA rappresenta la densità dell’aria; ricordando che:

PV = nRT (legge generale dei gas ideali) dove:

P rappresenta la pressione atmosferica (1 atm è circa uguale a 105 Pascal e 1 Pa = 1 N/m2);

V rappresenta il volume espresso in m3;

n rappresenta il numero delle moli espresso in mol = g/uma; si ha che n = massa/PM e considerando che l’aria è un miscuglio di vari gas, costituito soprattutto da azoto e ossigeno che ne rappresentano il 90 % PM, risulta costituito da 28 uma corrispondenti all’azoto a cui si somma 1 uma corrispondente all’ossigeno, all’argon e a gas rari;

T rappresenta la temperatura espressa in K; poiché la temperatura ambiente è di 20°C si deduce che la temperatura in Kelivin sia pari a 293 K (20 + 273 = 293);

si ha che:

R =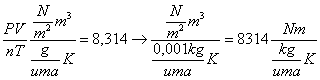

quindi si ottiene che:

rARIA = massa/Volume =  =

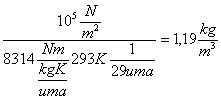
-AF rappresenta l’area frontale, che è una grandezza caratteristica, cioè è la dimensione di una parte di zona presa come riferimento per tutte le altre; l’AF è quella superficie presa come riferimento durante le prove. Determinata l’area frontale, i valori di forza e di pressione sono riferiti ad essa.

CR dipende quindi da Re, che per definizione risulta essere:

Re =

In cui:

-         u = velocità

-         D = diametro

-         r = densità

-         h = viscosità dinamica

Sapendo che =n, che rappresenta la viscosità cinematica del fluido, si ha che:

Re =

Il passaggio da moto laminare a moto turbolento avviene ad un valore di Re circa uguale a 3000, anche se realisticamente si ha il moto laminare per Re < 2300 e il moto turbolento per Re > 4100; all’interno di questo intervallo non è possibile determinare il comportamento del sistema; Re è un numero puro e non dipende dalle grandezze utilizzate.

Secondo i dati del nostro esercizio si ha:

Re = 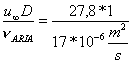= 1635000

In base al valore di Re trovato posso determinare il valore di CR consultando il seguente diagramma:

           

 

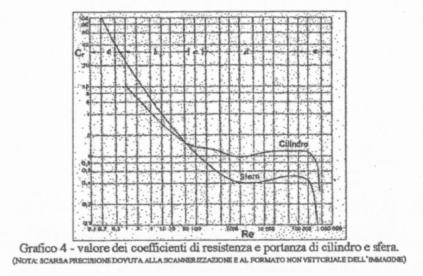
Þ CR = 0,15

Quindi, sostituendo nella formula della FT i valori numerici trovati si ha:

FT = 0,15*1/2*(27,8)2*1,19*1*15 = 1034,6 N

Infine, ricordando che ®  M=F*b*sen a , in cui F è la forza di trascinamento, b è uguale ad H/2 (il momento ribaltante è calcolato rispetto alla base) e a è uguale a 90°, si ha:

MF = FT*H/2 = 1034,6*15/2 = 7760 Nm

 

Esercizio 2

Determinare la risultante complessiva degli sforzi esercitati dal vento sulla base dei pali di una linea telefonica, ipotizzando che esso soffi perpendicolarmente rispetto alla superficie verticale dei pali; questi ultimi sono alti 10 m e distano l’uno dall’altro 50m, la velocità del vento è di 10 m/s.

 

 

 

 

 

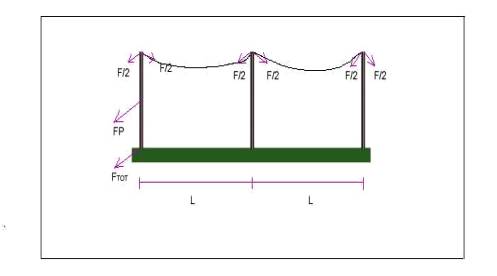
d = diametro cavo telefonico = 20 mm

D = diametro pali di sostegno = 100 mm

H = altezza pali di sostegno = 10 m

L = distanza tra un palo di sostegno e l’altro = 50 m

u¥ = velocità del vento = 10 m/s

FF = forza applicata dal filo al palo = ?

FTOT = forza complessiva alla base del palo = ?

 

La risultante degli sforzi alla base di un palo è data da tre componenti:

-         la forza che agisce sul filo alla destra del palo;

-         la forza che agisce sul filo alla sinistra del palo;

-         la forza che agisce sul palo stesso.

Ogni palo sopporta una forza dovuta a una quantità di filo L; la forza che agisce sul filo è intesa come forza di trascinamento e risulta quindi essere:

FFILO = CR FILO*1/2*rARIA*u¥2*AF

Si applica questa relazione ad un tratto di filo lungo L (L/2 a destra e L/2 a sinistra) e che ha quindi una AF = L*D. Per trovare il valore di FF si deve determinare il valore di CR, che è in funzione del numero di Reynolds, quindi:

ReF =

Da cui consegue, consultando il diagramma dell’esercizio precedente, il valore di CR:

CR = 1,2

Þ FF = 1,2*1/2*1,19*102*0,02*50 = 71,4 N

Si procede allo stesso modo per determinare il valore della forza che agisce sul palo stesso;si determina il valore di Re:

Re =

Da cui si ottiene:

CR PALO = 1,2

Quindi FPALO = CR P*1/2*rARIA*u¥2*AF = 1,2*1/2*1,19*102*0,1*10 = = 71,4 N

Si scopre dunque che FP FF sono identiche. La risultante complessiva degli sforzi esercitati sulla base dei pali si ottiene sommando le forze che agiscono sui filo a quella che agisce sul palo stesso:

FTOT = FF +FP = 71,4 + 71,4 = 142,8 N

Di conseguenza il momento flettente complessivo sarà uguale alla somma dei momenti riferiti a FP FF, cioè:

MTOT = MF + MP = FF*H + FP*H/2 (poiché è applicata nel baricentro del filo) = 71,4*10 + 71,4*10/2 = 1071 Nm

L’esercizio non presenta particolari difficoltà se non quella di determinare con precisione il CR in funzione di Re consultando il diagramma.

Esercizio 3

In questo esercizio si deve calcolare la velocità (u) a cui si stabilizza una goccia d’acqua mentre cade attraverso un fluido in questo caso costituito dall’aria.

D = diametro sfera = 1 mm

rSFERA = densità sfera = 1000 kg/m3

rARIA = densità aria = 1,19 kg/m3

CR = coefficiente di resistenza = ?

u = velocità di caduta = ?

Sottoposta ad azioni meccaniche la sfera tenderebbe a schiacciarsi e a diventare piatta, ma in questo ambito essa viene supposta sferica.

La sfera è sottoposta ad una forza peso applicata nel suo baricentro, che la spinge verso il basso e ad una forza di attrito viscoso rappresentante la resistenza che l’aria oppone alla caduta libera della goccia.

 

 

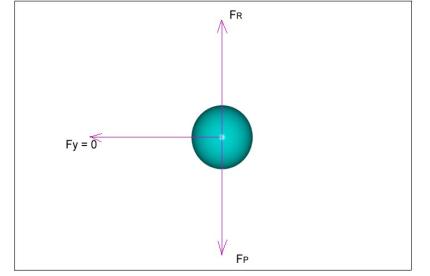
FP = forza peso = m*g (accelerazione di gravità)

FR = forza di attrito =CR*1/2*u2*rARIA*AF

Per i primi 100 m la FR è trascurabile, poi aumenta in quanto la resistenza dell’aria è in funzione della velocità di caduta al quadrato.

Nell’istante in cui la FR eguaglia il peso della sfera per il primo principio della dinamica (per il quale se un corpo era in quiete, resta tale; se era in moto permane di moto rettilineo uniforme)il moto della goccia diventa rettilineo uniforme, cioè essa continua la caduta libera ad con una velocità costante. E’ in questo ambito che si svolge l’esercizio.

FP = FR

m*g = CR*1/2*u2*rARIA*AF

Il valore della velocità di caduta si ottiene trovando i valori di volume e area frontale della sfera:

m = VSFERA*rSFERA = 1/6pD3*rSFERA*AF (pD2/4)

Þ g*1/6 pD3*rSFERA = CR*1/2*u2*rARIA*(pD2/4)

u =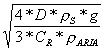

Si nota quindi che la velocità di caduta cresce con la radica quadrata del diametro in modo non lineare, ma si può comunque dedurre che un corpo grosso cade più velocemente di uno piccolo.

Per trovare il valore della velocità devo calcolare il CR, che però si ottiene calcolando Re:

Re =

Ma Re è in funzione della velocità, che è ciò che stiamo cercando, perciò è necessario procedere per via iterativa.

Allora si prende una velocità di prova per utilizzare una prima volta il diagramma in cui sono contenuti i valori del CR in funzione di Re.

Purtroppo in questo caso non abbiamo dei limiti per i valori di prova, quindi diamo casualmente a u un valore.

u’ = 10 m/s

Re’ =  =

Dal grafico ricavo il valore di CR ® 0,55

u = 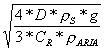 = = 4,47 m/s

Si continua per tentativi fino a quando il valore della velocità si discosta da quello precedentemente calcolato di una quantità inferiore alla tolleranza richiesta(15%).

u’’ = 5 m/s

Re’’ = 294 ® CR = 0,70

u =  3,96 m7s

u’’’ = 4 m/s

Re’’’ =  235 ® CR = 0,75

u =  3,83 m/s

Il valore deve essere intorno al 3,7 m/s, quindi 3,83 è entro i limiti di tolleranza (3,83*15/100).

Per la sfera il grafico può fornire valori uguali del CR per diversi numeri di Reynolds, da ciò il calcolo può risultare leggermente impreciso.

 

Esercizio 4

Dal manuale dell’ingegnere apprendiamo che secondo le normative Enel:

-         se il vento soffia con una velocità (u¥) pari a 65 km/h

Þ la pressione di trascinamento (PT) è uguale a 18 kgFORZA/m2

-         se, invece, il vento soffia con una u¥ pari a 130 km/h

Þ la PT è uguale a 72 kgFORZA/m2

Dunque:

u’¥ = 65 km/h

P’T = 18 kgF/m2

u’’¥ = 130 km/h

P’’T = 72 kgF/m2

Tenendo presenti queste premesse si consideri un filo conduttore avente queste caratteristiche:

 

 

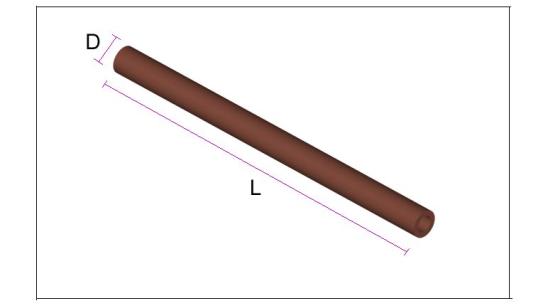
L = lunghezza filo = 1 m

D = diametro filo = 10 mm = 0,01 m

Dopo aver espresso la velocità del vento in m/s come richiesto dal sistema internazionale (S.I.):

u’¥ = 65*1000/3600 = 18 m/s

u’’¥ = 130*1000/3600 = 36 m/s

Si intende verificare i valori dati dal manuale riguardo a P’T e a P’’T quindi si ricalcolando le due pressioni; la formula che esprime la pressione di trascinamento è:

PT = F/S = = CR*1/2*rFILO*u2¥*AFILO

Per determinare le due pressioni si devono calcolare i rispettivi numeri di Reynolds al fine di trovare C’R C’’R; allora.

Re’ =  = 10621

Da cui ® C’R = 1,15

Þ P’T = 1,15*1/2*(18)2*1,19 = 221,7 Pa @ 22,6 kgF/m2

si procede allo stesso modo per P’’T:

Re’ =  = 21176

Da cui ® C’’R = 1,2

Þ P’’T = 1,2*1/2*(36)2*1,19 = 925 Pa @ 94 kgF/m2

Le pressioni di trascinamento ricalcolate non coincidono con quelle fornite dal manuale dell’ingegnere, poiché al variare del diametro del filo varia anche il numero di Reynolds, che modifica a sua volta la pressione di trascinamento; d’altra parte chi ha mai detto che la fisica è una scienza esatta ?!

 

Esercizio 5

Riguardo alla spinta che il vento esercita sulla facciata di una casa esiste una tabella presa dal manuale dell’ingegnere in cui vi sono i valori della pressione di trascinamento in kgFORZA:

                  h                                                    PT

         tra 0 e 10 m                                    50 kgFORZA/m2

       tra 10 e 50 m                                   100 kgFORZA/m2

       tra 50 e 100 m                              150 ¸240 kgFORZA/m2

           > 100 m                                       240 kgFORZA/m2

Alla base dell’edificio la pressione è molto bassa; sarà, invece, massima ai vertici dell’edificio.

Se la velocità del vento (u¥) è pari a 60 km/h e il palazzo è alto 10 m, determinare il valore del coefficiente di resistenza, che mi viene fornito da una pressione di trascinamento pari a 50 kgFORZA/m2.

H = altezza palazzo = 10 m

L = larghezza palazzo = 1 m

u¥ = 60 km/h

 

 

 

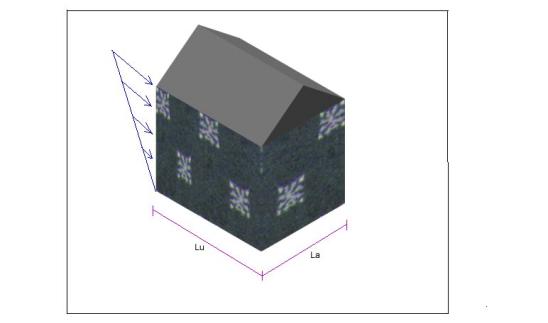
Ricordando la formula della forza di trascinamento si ha:

FT = CR*1/2*u2¥*rF *AF

In cui AF = 10*1 = 10 m2

Ma si ha anche che:

FT = PT*AF = 50*9,81*10 = 4905 N

Da qui si ottiene infine CR, che è:

CR =

Poiché il valore di CR >1 si nota che si è tenuto conto nel costruire l’edificio della variabilità spaziale (da punto a punto) e temporale (nello scorrere del tempo) del fenomeno, il CR cioè è già stato maggiorato rispetto al suo valore teorico:

componente aerodinamica + coefficiente di sicurezza = CR = 2,95

Non è, infatti sicuro assumere il coefficiente di una casa uguale a 1, poiché occorrono valori che tutelino l’edificio.

 

I vortici di von Karman

Quando un corpo cilindrico e simmetrico viene investito dal vento o da un altro fluido si creano fenomeni vorticosi il più delle volte instabili, simili a quelli che si creano quando un fluido scorre con moto laminare all’interno di un tubo o quando si verifica il passaggio dal moto laminare a quello turbolento.

I vortici di von karman sono noti soprattutto perché sono legati ai problemi di risonanza strutturale, che si verificano per determinate frequenze; i problemi consistono nel fatto che per particolari valori di queste frequenze il fluido si propaga con moto oscillatorio e ciò può procurare non pochi problemi alle strutture, basti ricordare il crollo del ponte sul fiume Potomac o i recenti problemi di risonanza dati dal vento e dal passaggio di persone al Millenium Bridge, a causa dei quali è al momento chiuso.

Un importante accorgimento per evitare le risonanze consiste nel porre corde arrotolate lungo i piedritti del ponte: l’effetto spirale impedisce lo sviluppo del vortice!