Fluidodinamica - Esercizi-
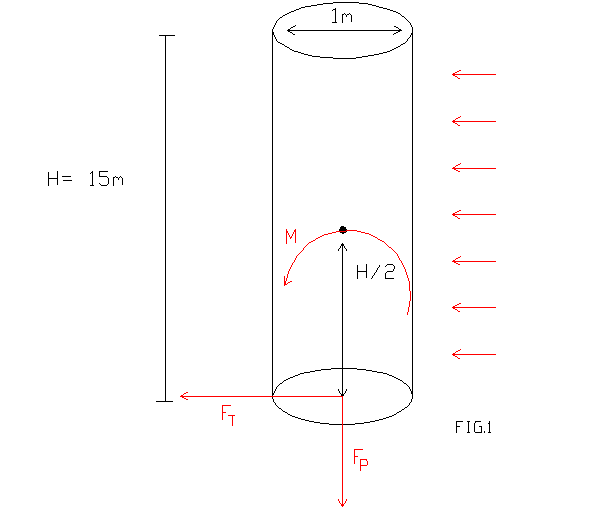
ESERCIZIO 1 : Spinta del vento su un camino
Determinare la risultante complessiva degli sforzi ed il momento flettente, dovuti alla spinta del vento su un camino cilindrico alto 15 m e con diametro 1m. Il vento ha una velocità di 100 km/h e la sua direzione è perpendicolare al camino.
Dati:
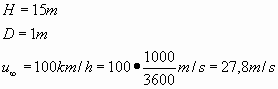
La formula della forza di trascinamento è :
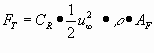(1)
Dove : 
coefficiente di resistenza (caratteristico delle varie forme geometriche)
velocità del vento
densita’ del fluido (aria)
area frontale
Il coefficiente 
si ricava dal diagramma se si conosce il numero di Reynolds:
=
(2)
Nel nostro caso 
e la viscosità cinematica dell’aria si trova nelle tabelle,
pertanto:
e ad esso corrisponde il valore di 
.
La densità dell’aria 
si ricava dall’equazione dei gas perfetti. La massa molare dell’aria è 29 kg/kmol e, in condizioni normali di pressione e temperatura, abbiamo:
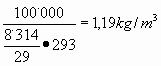(3)
L’area frontale 
è l’area del rettangolo di dimensioni H e D.
La forza di trascinamento è quindi:
Il momento flettente, che tende a ribaltare il camino, si applica nel baricentro ed è dato da:
(4)
ESERCIZIO 2
In una linea elettrica i diametri dei pali e dei fili sono rispettivamente 
e 
I pali distano tra loro 50
e sono alti 10.
Il vento soffia in direzione ortogonale alla linea con una velocita’ di 10 
.
Determinare la forza di trascinamento del filo sul palo, quella complessiva alla base del palo ed il momento flettente totale.
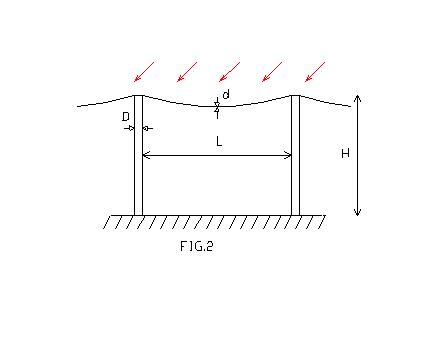
Dati:
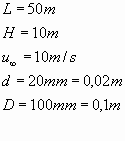
Ogni palo deve sopportare una forza dovuta ad un tratto di filo di lunghezza L ( L/2 a destra e L/2 a sinistra ). Lo sforzo totale è la somma della forza agente sul filo e di quella agente sul palo. La forza di trascinamento è data dalla formula:
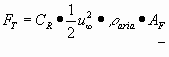
Calcolo il numero di Reynolds per il filo:
e dal diagramma ricavo 
Faccio lo stesso per il palo:
e dal diagramma ricavo 
Area frontale del filo
Area frontale del palo
(calcolata nell’ESERCIZIO1)
Calcolo le forze di trascinamento :
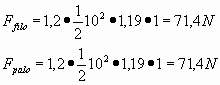
La forza complessiva è quindi :
Il momento flettente totale è dato dalla somma del momento flettente esercitato dal filo (braccio 
) e di quello esercitato dal palo ( braccio 
)
ESERCIZIO 3 : Goccia che cade
Una goccia di pioggia di forma sferica, avente diametro 
e densità 
, cade nell’aria senza deformarsi .Conoscendo la densità dell’aria 
calcolare la velocità di caduta della goccia.
Sulla goccia agiscono :.
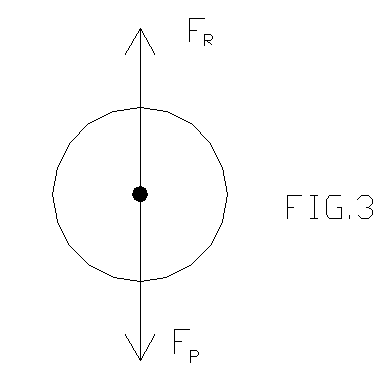
-la forza peso 
diretta verso il basso (5)
-la forza resistente di attrito 
diretta verso l’alto
La velocità di caduta è uniforme quando le due forze sono uguali:
(6)
è il volume della goccia e 
la sua area frontale che, in funzione del diametro D, sono:
e 
(7)
Sostituendo si ottiene
(8)
Dopo aver semplificato ricaviamo la velocità 
(9)
si ricava dal numero di Reynolds
Poichè anche 
dipende dalla velocità devo procedere per tentativi ipotizzando valori di velocità.
1° tentativo:
Ipotizzo 
Avrò 
e 
(10)
Calcolo la velocità 
sostituendo a 
il valore 
trovato e ottengo
(11)
che risulta essere meno della metà del valore ipotizzato.
2° tentativo:
Ipotizzo 
Avrò 
3° tentativo:
Ipotizzo 
Avrò 
Procedo finchè il valore di velocità si discosta da quello calcolato in precedenza di una quantità minore della tolleranza richiesta.
Se la tolleranza fosse del 15% il risultato finale può essere 
.
ESERCIZIO 4 : Norme per un filo elettrico
I dati suggeriti dalla normativa Enel per i cavi elettrici (riferiti alla sezione frontale) sono:
1) 
(velocità del vento)
(pressione di trascinamento)
2) 
Verifichiamoli:
Supponiamo di avere un filo di diametro 
e lungo 
.
La pressione di trascinamento è data da :
(12)
Calcoliamo il numero di Reynolds per i 2 casi:
La viscosità cinematica dell’aria si trova nelle tabelle 
D=
Nel caso 1) 
nel diagramma trovo 
Nel caso 2) 
nel diagramma trovo 
La pressione di trascinamento è:
con 
Nel caso 1) 
Nel caso 2) 
Si trovano valori superiori a quelli stabiliti dall’Enel.
ESERCIZIO 5: Spinta del vento su una facciata di un edificio
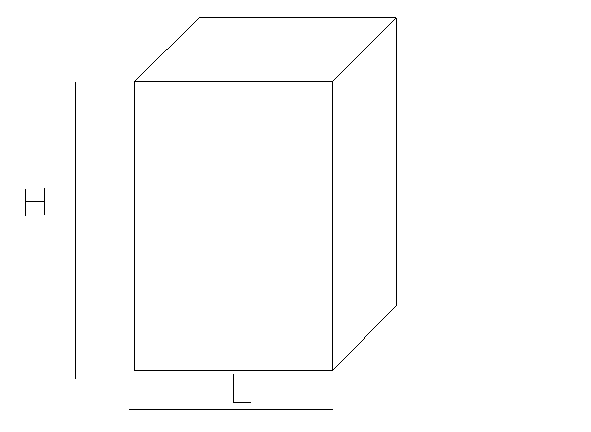Dato un vento che soffia ad una velocità 
ed un palazzo alto 
, vogliamo determinare il valore di 
che è stato utilizzato per ricavare il valore 
riportato nella tabella 1.
Dati:
Esistono norme in funzione dell’altezza dal suolo: ( Tabella 1 )
|
Altezza |
Pressione |
|
0 |
50 |
|
10 |
100 |
|
50 |
150 |
|
> 100 |
240 |
La forza di trascinamento può essere calcolata in 2 modi:
(13)
(14)
Uguagliando le due espressioni si ottiene
(15)
Da cui si ricava la seguente espressione per :
(16)
Nel nostro caso:
Il valore è maggiore rispetto al valore teorico.
VORTICI DI VON KARMAN
I vortici di Von Karman sono un fenomeno di instabilità fluidodinamica molto pericoloso per le strutture snelle.
Nelle strutture simmetriche il vento provoca vortici sfalsati aventi una determinata frequenza di oscillazione.
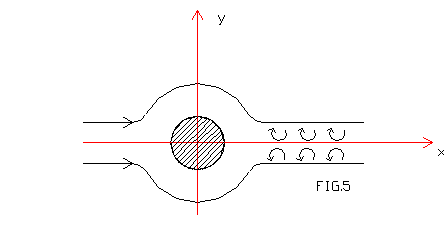
Come un diapason, ogni struttura ha la sua frequenza di risonanza.
Esiste una frequenza di eccitazione legata a 
.Se le due frequenze coincidono ne deriva un’oscillazione che fa vibrare sempre di piu’ la struttura fino a provocarne il crollo.
L’effetto finale può essere 100 volte superiore a quello supposto.
Due casi famosi sono:
-il Ponte sul fiume Potomac, una struttura metallica molto snella degli anni ’30, che è crollato a causa di una tempesta di vento.
-Il Millenium Bridge a Londra, ponte pedonale che ha manifestato esempi di risonanza sia dovuti al vento che al calpestio delle persone.
Per rompere i vortici di Von Karman si avvolgono a spirale dei lamierini metallici alla struttura. Lo stesso accorgimento è adottato nelle antenne delle automobili. Eliminando questi vortici si elimina anche il fischio che essi provocano.
Il Ponte di Brooklyn non presenta questo tipo di inconveniente perchè sia la funicolare che i tiranti sono delle corde arrotolate.
10 
