Applicazioni
ai concetti di coefficiente economico e di coefficiente economico della
macchina di Carnot.
L’energia prodotta da un
combustibile (ad esempio il metano, il carbone, il gasolio) durante il processo
di combustione, viene quantificata attraverso il potere calorifico.
Si supponga di disporre
di una quantità pari a 1kg di un combustibile qualunque.
Esso reagirà nel processo
di combustione, che nient’altro è se non un processo di combinazione chimica
delle sostanze ossidabili di cui è fatto il materiale con l’ossigeno contenuto
nell’aria, con N kg di ossigeno (con N>1 dipendente dalle reazioni chimiche
che devono avvenire e dalla composizione chimica del materiale).
Quindi la reazione
chimica alla base del processo di combustione sopra descritto è la seguente:
Mcomb = 1kg M+N+1kg di prodotti di combustione CO2
MN2 = M kg ↓ N2
Nella massa totale di fumi
prodotti dalla reazione, compare una certa quantità d’azoto pari a M kg dovuta al fatto che il processo di combustione
non avviene con l’ossigeno puro, ma con l’aria.
Affinchè la combustione
avvenga in modo esatto e soddisfacente, dobbiamo far si che ogni molecola
di ossigeno dell’aria venga impiegata nella reazione con il combustibile,
ottenendo così il rapporto esatto tra la massa del combustibile e la massa del
comburente, che è l’aria (rapporto
stechiometrico di masse).
rapporto stechiometrico di masse : 
Considero ora un
recipiente rettangolare posto in un ambiente isolato dal punto di vista termico
contenente una quantità pari ad 1kg di combustibile e tutta l’aria di cui il
combustibile ha bisogno perché la combustione avvenga con il rapporto
stechiometrico di masse esatto.
Sia l’aria che il
combustibile sono a temperatura ambiente.
Il valore della
temperatura adiabatica varia da combustibile a combustibile e quindi non è un
valore generalizzabile.
Sottraendo al nostro
recipiente energia sotto forma di calore ΔQ
ΔQ = Cv · Mf
· (T1-T2)
Dove Cv
esprime il calore specifico a volume costante
Mf
la massa complessiva dei fumi
T1 la temperatura adiabatica
T2 energia sottratta sotto forma di calore
i
fumi si raffreddano e quindi anche il loro potere calorifico diminuisce, ma in
modo non proporzionale alla sottrazione di calore.
Tracciando un grafico in
cui in ascissa si esprime la quantità di calore che sottraiamo volta per
volta al sistema una volta avvenuta la
combustione, e in ordinata la variazione di temperatura del sistema stesso
conseguente a tale processo, supponendo il volume specifico costante, si
ottiene una curva (resa graficamente con una retta per agevolarne la lettura)
decrescente con la temperatura che riduce però visibilmente la sua pendenza in
prossimità di una particolare temperatura, detta temperatura di rugiada, dell’ordine di circa 50°C.
A tale temperatura infatti succede un passaggio molto importante del processo di combustione: il vapore acqueo prodotto dalla reazione si condensa liberando una grande quantità di energia convertita in calore (calore latente di vaporizzazione).
In tal modo riesco a
sottrarre una percentuale di calore considerevole senza avere una grossa
riduzione di temperatura.
Incontrato questo valore
in ordinata, la curva descritta nel grafico non decresce più linearmente, ma si
assesta dolcemente fino alla linea di quota della temperatura ambiente di 20°C.
Questa è la cosiddetta curva di raffreddamento dei fumi.
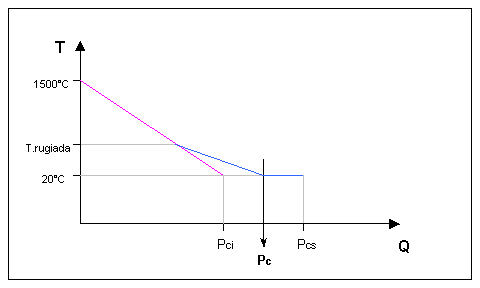
Fig.1: Grafico
temperatura fumi – calore ceduto ( P = 1 atm).
Una
prima considerazione che si può fare è che non essendo costante l’energia,
sotto forma di calore, rilasciata dai
fumi, neanche il potere calorifico sarà costante.
Nel grafico il potere calorifico è
determinato dall’intersezione della curva di raffreddamento dei fumi con la
linea di pendenza minore propria della temperatura di rugiada.
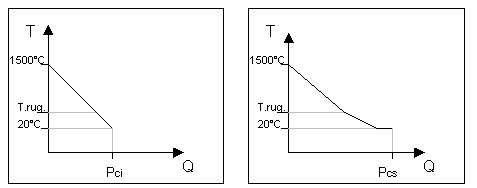
Fig.2:
Grafico del potere calorifico inferiore e superiore.
Siccome poi a momenti diversi di combustione, corrispondono diverse quantità di vapore acque contenute in esso, sono stati definiti due ulteriori varianti del potere calorifico:
–)
il potere calorifico inferiore (Pci) definito come la
quantità di calore che si ottiene ipotizzando che il vapore acqueo non
condensi, quindi proseguendo quella retta che avrei avuto se non si fosse
verificato il fenomeno di rugiada;
–)
il potere calorifico superiore (Pcs) definito come la
quantità di calore che si ottiene facendo condensare completamente il vapore
acqueo.
Allora calcolando 1
BTU/lb = 2,33 kJ/kg
Ora possiamo subito
calcolare la potenza termica Q1 sviluppata dalla caldaia:
Q1 = 
= 32.620.000 kJ/h =
= 9061 kJ/h
Conoscendo il rendimento
della macchina ed avendo le temperature di margine, siamo in grado di calcolare
il coefficiente economico della macchina di Carnot:
εc = 1-
= 0,21 ← basso coefficiente economico di
Carnot
Il rendimento reale della
nostra macchina sarà ora facile da trovare, sapendo il rendimento
termodinamico. Infatti
ε = 
= 0,21 · 0,25 = 0,054 = 
La Potenza necessaria per
mettere in moto la locomotiva è quindi pari a:
L = 
= 0,054 
= 489 kw
Tale potenza è esatta se
consideriamo l'attrito dell'aria e delle rotaie già compresi nel rendimento
termodinamico oppure trascurabili.
Sapendo che :
L = 
=
= 
=1,79 km
L'altezza che la
locomotiva percorre in un'ora è:
H = 
= 
= 1,79 km
Sapendo che la locomotiva percorre in
un'ora il tratto di strada l =80 km, l'angolo θ di pendenza della salita
che la macchina deve sostenere è facilmente determinabile tramite le relazioni
trigonometriche:
θ = arcsen 
= arcsen
= 0,022378
rad = 1,282°
2) Si supponga di dover riscaldare un'abitazione alla
temperatura di 20°C, quando all'esterno la temperatura è di -5°C. Sapendo che
la potenza necessaria a mantenere tale temperatura interna è di 1kw, studiare
le possibili strutture affinchè vengano rispettate le condizioni suddette.
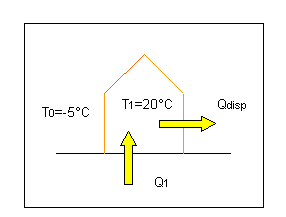
Fig.5: Casa da riscaldare secondo le temperature di progetto.
L'involucro della casa tende a disperdere una
certa potenza termica; dunque per garantire che la temperatura interna della
casa rimanga di 20°C, dobbiamo apportare una quantità di calore Q1 uguale a quella che l'abitazione consuma e
cioè 1kw, creando un flusso di calore continuo.
Esistono due modi per
fornire questo 1kw alla mia abitazione:
A) tramite resistenza elettrica;
B) tramite pompa di calore.
Quale delle due soluzioni
è la più proficua in termini di lavoro minimo?
Caso
A): Resistenza elettrica
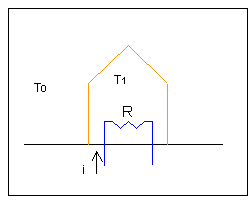
Fig.6: Schema del
problema.
Consiste nell'applicare
un generatore di corrente elettrica.
Il calore da fornire alla
casa è uguale alla potenza elettrica.
Q1 = 
= 1kw
Caso B): Pompa di calore.
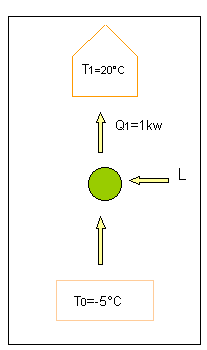
Fig.7:
Schema del problema.
Consiste nel prelevare
calore dall'ambiente esterno che ha la temperatura T0 pari a -5°C
per dare alla casa il calore Q1.
Conoscendo la temperatura interna e quella esterna
della casa, allora la mia pompa di calore è una macchina reversibile che lavora
con il coefficiente di Carnot.
εc = 
= 1-
= 0,085324 kw
Questo coefficiente
economico esprime il rapporto tra lavoro e calore specifico, ma il calore Q1 deve essere 100 kw quindi
la potenza elettrica impegnata deve essere 100 kw.
ηpompacalore = COP
= 
= 11,7
Il COP (coefficiente di
prestazione) indica il rapporto tra energia ottenuta e l'energia spesa ed è
calcolabile solo nelle pompe di calore.
Se volessi dare
all'ambiente esterno un valore di -10°C, per avere un dispositivo vantaggioso
in termini di lavoro minimo, dovrò considerare la temperatura della batteria
della pompa di calore più elevata di quella del precedente sistema: quindi la
mia macchina non lavorerà più tra -5°C e 20°C, ma tra -10°C e 40°C.
In condizioni reali di riscaldamento dunque:
εc
= 1 -
= 0,16 kw
Quindi la potenza è L = 160 w. Infine se considero la mia
pompa una macchina perfettamente reversibile avrò:
COP = 
= 6,2
In conclusione usando 20
w elettrici possiamo trovare una potenza elettrica di 5 watt che tutto sommato
è un ottimo risultato.
Un'ulteriore possibilità
di riscaldamento per la mia abitazione
potrebbe essere quella che mi porta ad utilizzare un sistema combinato
centrale termica - pompa di calore.
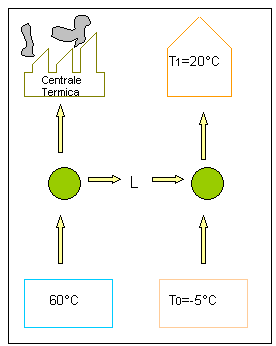
Fig.8: Schema del
problema.
Nella centrale termica si
brucia del gas per raggiungere la temperatura di 500°C con una potenza pari a
0,2 kw per un certo processo di produzione. La macchina della centrale lavora
tra le due temperature di 500°C e 60°C.
Il lavoro prodotto dalla
centrale può essere utilizzato da una pompa di calore la cui potenza è di 1kw;
il calore del serbatoio a 60°C può servire per produrre altra energia. Al posto
di bruciare gas direttamente nella casa con grosse perdite di calore, con il
passaggio intermedio a 60°C si cerca di sfruttare al meglio tutta l'energia
conseguente alla combustione del gas.
Vediamo ora se tale
struttura può essere vantaggiosa in termini di lavoro energetico.
Considerando il
rendimento reale della macchina e sapendo che L = 0,2 kw quanto calore devo usare per produrre questi 0,2 kw?
Per il Teorema di Carnot
so che:
εc = 1-
= 0,65 kw
Se la macchina del primo
sistema ha prodotto un lavoro pari a 0,2 kw questo è uguale a 0,05 volte la
potenza primaria Qp che io ho sottratto alla sorgente di calore.
Quindi :
L = 0,2 kw = 0,65
=
= 0,30 kw
Rispetto a bruciare il
gas direttamente nell'abitazione, se lo brucio in centrale, produco energia
elettrica e la utilizzo tramite pompa di calore, per scaldare la casa
risparmierò 2/3 del combustibile usato in precedenza .
Un esempio famoso di come
questo sistema sia vantaggioso, è dato dalla città di Brescia.
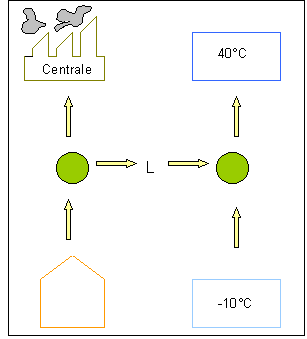
Fig.9: Schema del
problema.
Qui trattandosi di una
macchina reversibile posso calcolare il coefficiente economico della macchina
di Carnot:
εc
= 1- 
kw
Bruciando 1 kw di gasolio in centrale ne utilizzo 0,46
kw per riscaldare le case, 0,54 kw per la pompa di calore. L'efficienza di tale
riscaldamento è espressa dal CUC
definito come il rapporto tra energia ottenuta e quella spesa:
CUC
=
kw → Valore un
po’ ingigantito rispetto la reltà perché
il CUC teorico massimo è 2.
Otterrò dunque 3,2 kJ
bruciando 1 kJ. La soluzione combinata attuata a Brescia, rappresenta per tanto
un'alternativa più che valida.