Marco Tapinelli matr.110731
Lezione del 6/12/99
ore 16:30-18:30
Analisi in frequenza
Indice:
1-Spettro di un segnale
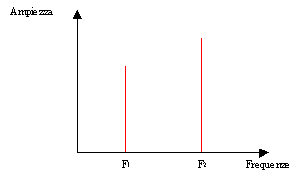
Fino ad ora abbiamo utilizzato una sola modalità di rappresentazione di un segnale sonoro vale a dire quella nel dominio del tempo; è di notevole interesse però anche il contenuto energetico delle varie frequenze che lo compongono. Quest’ultima analisi si può ottenere tramite lo "spettro del suono", in pratica una rappresentazione grafica su diagramma cartesiano, avente in ascisse le frequenze e in ordinate le ampiezze.
Per operare l’analisi in frequenza occorre partire dalla forma d’onda del segnale, molto probabilmente di tipo elettrico perché prelevata da un microfono, e operare una conversione.
E’ importante notare che tutte le tecniche di conversione sono imperfette, in altre parole non esistono strumenti di misura o tecniche matematiche che permettono di riprodurre con precisione i fenomeni d’analisi in frequenza che avvengono nel nostro orecchio.

Figura 1 - Spettro di un segnale composto da due diverse frequenze -
Per operare la conversione occorre distinguere due casi:
Nel primo caso ci si riferisce a segnali sempre uguali a se stessi di cui possiamo quindi analizzare le frequenze una alla volta e mettere insieme i risultati: perciò l’analisi frequenziale è tanto semplice che i sistemi di conversione eguagliano e a volte superano, la percezione umana. Un motore elettrico, una volta avviato a velocità costante, è un esempio di sorgente di segnale stazionario.
Nel secondo caso invece, si prendono in considerazione segnali che variano in maniera non prevedibile nel tempo e quindi l'analisi non riesce ad eguagliare le capacità umane.
2-Analisi segnali stazionari
Analizziamo le tecniche di conversione per i segnali stazionari. Il primo metodo (anni '60) fu quello del "Banco di filtri": si dispone di una serie di filtri passa-banda (tipicamente 10 filtri d’ottava), attraverso un selettore si varia il percorso del segnale elettrico in modo che entri in uno dei filtri e all’uscita di quest’ultimo si va ad un misuratore, solitamente un voltmetro a lancetta.
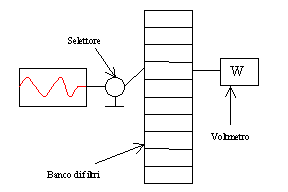
Figura 2 – Banco di filtri -
Tramite quest’attrezzo si misura l’intensità di ciascuna frequenza che poi è riportata sul diagramma spettrale.
Un filtro d’ottava è un bassa-banda, in altre parole, un dispositivo passivo che lascia passare inalterate le frequenze contenute in un certo intervallo mentre blocca quelle che si trovano al di fuori di questo.
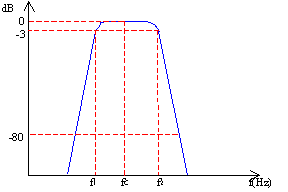
Figura 3 - Risposta del filtro d’ottava –
In un filtro di questo tipo si individuano due caratteristiche principali:
): vale a dire la distanza dei punti situati ad un guadagno di –3dB rispetto a quello di centro banda cioè fra le due frequenze di taglio:
![]()
![]() (1
(1
In un filtro ideale la pendenza dei fianchi è di 90° mentre in quelli reali è minore, per fare in modo che la misura sia più precisa possibile, la pendenza deve essere compresa in maschere d’accettabilità previste dalle norme IEC (International Eletrotechnical Commission) più precisamente dalla norma : IEC 1260:1995-08 oppure CEI EN 61260.
3-Analisi di segnali transienti
Lo studio di un segnale transiente è effettuato anch'esso con l’utilizzo di un banco di filtri, ma ora il segnale è mandato contemporaneamente a tutti i filtri e le loro uscite sono misurate da un numero di voltmetri pari a quello dei filtri.
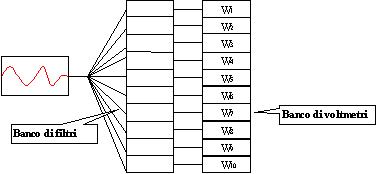
Figura 4 – Analizzatore di segnali transienti
Con un oggetto di questo tipo misuriamo l’ampiezza di tutte le frequenze simultaneamente, da questo il nome "analizzatore in tempo reale" o RTA (Real Time Analaised).I filtri ad ottave hanno una larghezza di banda abbastanza elevata (il rapporto tra frequenze di taglio inferiore e superiore è di ½), quindi esiste l’esigenza di utilizzare filtri a banda più stretta, vale a dire a frazione d’ottava, mantenendo però il concetto di proporzionalità tra ampiezza di banda e frequenza di centro banda, infatti nei filtri d’ottava per ogni banda si dovrà avere
![]() (2
(2
Nei filtri a 1000 Hz ![]() (3
(3
Nei filtri a 500 Hz ![]() (4
(4
Il secondo filtro ha una fC più bassa ma è anche più "stretto".
I filtri che hanno questo rapporto costante sono chiamati FILTRI AD AMPIEZZA PERCENTUALE COSTANTE: attraverso questa caratteristica si fa in modo che la frequenza f2 di ogni filtro diventi la frequenza f1 del filtro successivo, in modo da coprire completamente tutto l’intervallo di frequenza interessato. Per esempio, avendo una sinusoide che varia la sua frequenza fino a coprire tutto il campo coperto dai filtri, si avrà un’eccitazione di questi ultimi in successione, mentre l’energia totale del banco rimarrà costante in ogni istante non essendo presenti buchi tra filtro e filtro o rilevanti sovrapposizioni.
Le curve di risposta dei filtri s’incontrano in punti caratterizzati da un guadagno di –3dB vale a dire che l’energia si distribuisce metà in un filtro e metà in quello successivo.
I filtri più utilizzati sono:
Prendiamo in esame, per esempio, i filtri da 1/3 l’ottava: così facendo l’ottava dei 1000 Hz sarà coperta da tre filtri aventi le seguenti frequenze di taglio: 800 Hz, 1000 Hz, 1250 Hz. Infatti :
Sappiamo che ![]() Hz e
Hz e ![]() Hz (5
Hz (5
La prima condizione è:
![]() (6
(6
Deve essere soddisfatta la condizione 2, quindi:
![]() (7
(7
Ora definiamo:
![]() (8
(8
Per la definizione d'ottava:
![]() quindi
quindi ![]() (9
(9
Se partiamo da ![]() Hz :
Hz :
![]() Hz
Hz
![]() Hz (10
Hz (10
![]() Hz
Hz
Conoscendo le frequenze di taglio:
![]()
Per la condizione 7 si avrà:
![]() Hz e
Hz e ![]() Hz (11
Hz (11
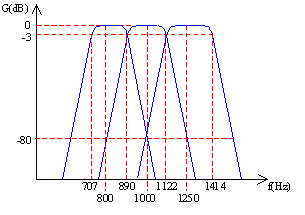
Figura 5 – Tre filtri da 1/3 l’ottava -
Un suono ad una sola frequenza pari ad una delle frequenze di taglio da luogo ad uno spettro contenente il segnale non in una sola banda ma in due, ciò dimostra che la selettività non è mai completa
4-Analisi in banda stretta
Esiste una seconda metodologia d’analisi del suono, resa possibile dall’avvento dei computers, chiamata "analisi in banda stretta" o "analisi di Fourier"; lo spettro del segnale si costruisce attraverso un’operazione matematica detta Trasformata discreta di Fourier (Discrete Fourier Transport – DFT). Un’analisi di questo tipo è possibile solo con l’uso di calcolatori e oltre all’ipotesi di stazionarietà del segnale, richiede anche la periodicità, quindi non può essere utilizzata per segnali che variano in modo imprevedibile come la voce umana.
La base matematica su cui si appoggia l’analisi di Fourier è il TEOREMA DI FOURIER:
"un suono complesso, ma periodico, è sempre rappresentabile dalla sovrapposizione di un infinito numero d’onde sinusoidali ciascuna dotata d’opportuna ampiezza e fase."
Un suono periodico che chiameremo P(t), in quanto proveniente da un microfono e quindi proporzionale alla pressione, potrà essere espresso con la seguente formula:
![]()
![]() (12
(12
Ovviamente nella realtà non possiamo calcolare un numero infinito di sinusoidi e le tecniche d’elaborazione matematica rendono facile il calcolo delle ampiezze e delle fasi per rappresentare il suono solo se le frequenze variano con una legge logica, quindi la regola utilizzata è quella di avere un numero finito di componenti frequenziali equidistanti tra loro.
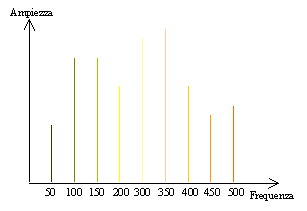
Figura 6 - Spettro di un segnale -
Lo spettro in figura non è stato ricavato dal teorema di Fourier, ma da un suo derivato ottenuto operando delle discretizzazioni(da questo il nome Trasformata discreta di Fourier). Ora però non siamo più in grado di variare a nostro piacimento ampiezze e frequenze in quanto sono legate a regole matematiche. Un’analisi di questo tipo mi dà un’altra informazione oltre l’ampiezza, vale a dire la fase, che normalmente viene erroneamente ignorata: senza di essa infatti non siamo in grado di ricostruire il segnale di partenza. Non è importante la fase assoluta ma quella relativa: infatti variando quest’ultima, si arriva ad un segnale completamente differente da quello iniziale; quest’artificio è utilizzato per rendere le trasmissioni incomprensibili: la sorgente del segnale varia la fase di ogni componente spettrale attraverso un algoritmo pseudocasuale da questo segnale distorto potrà risalire a quello originale solo chi possiede l’algoritmo decriptatore.
La rappresentazione dello spettro di un suono può variare notevolmente a causa delle varie modalità di rappresentazione. La rappresentazione a bande percentuali si presta ad essere disegnata con asse delle frequenze logaritmico, perché così facendo tutte le bande a 1/3 d’ottava risultano della stessa ampiezza, mentre l’analisi in banda stretta è ragionevole rappresentarla con l’asse delle frequenze lineare.
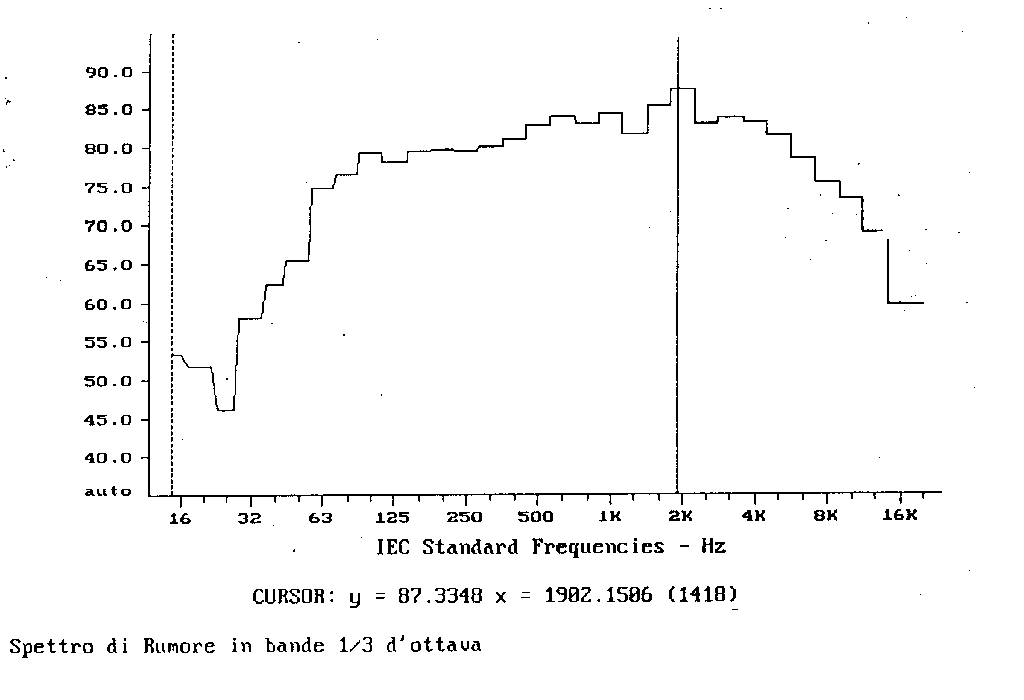
Figura 7 - Spettro in terzi d'ottava con scala delle frequenze logaritmica -
In figura 7 è rappresentato lo spettro di un segnale ottenuto tramite un banco di filtri da 1/3 d’ottava (ogni segmento orizzontale rappresenta una banda ampia 1/3 d’ottava) con l’asse delle frequenze logaritmico, secondo la spaziatura standard IEC.
A prima vista si potrebbe dedurre che il segnale è ricco d’alte frequenze e che il picco massimo si trova a 1902 Hz.
Passiamo ora all’analisi in banda stretta mantenendo però inalterata l’asse delle frequenze:
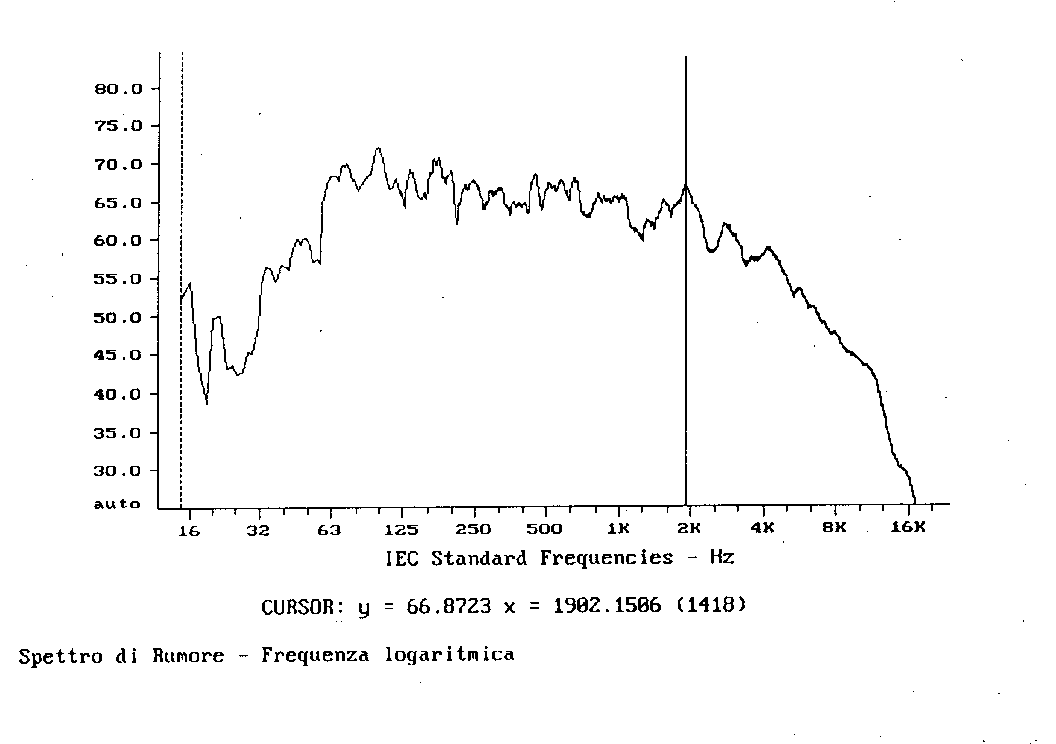
Figura 8 - Spettro in banda stretta con scala delle frequenze logaritmica -
In questo spettro vediamo che alla frequenza di 1902,1 Hz non è più presente il picco massimo, infatti il suo valore è sceso da 87,3 dB a 66,8 dB!
Il motivo di queste differenze e che nel primo caso, l’ampiezza di banda dei filtri aumenta proporzionatamente con la frequenza, vale a dire che finestre di terzi d’ottava a basse frequenze catturano una finestra di bande strette più piccola che non quelle ad alte frequenze. Questa caratteristica si nota ancora meglio se visualizziamo lo spettro in terzi d’ottava con l’asse delle frequenze lineare.
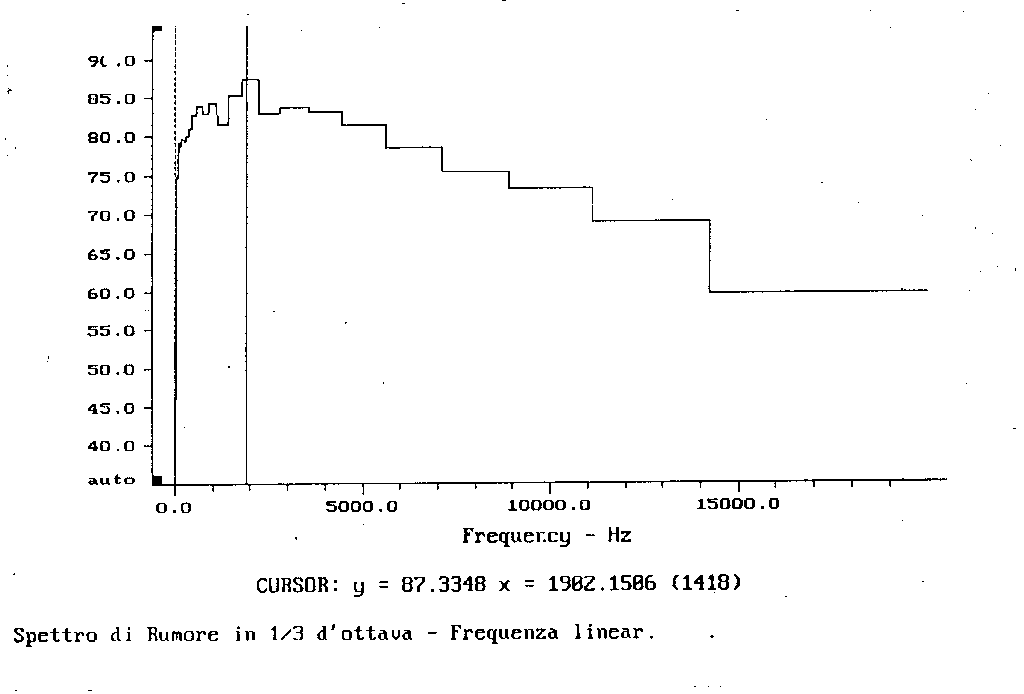
Figura 9 - Spettro in terzi d'ottava con scala delle frequenze lineare -
Ora vediamo lo spettro dello stesso segnale disegnato tramite l’analisi in bande strette:
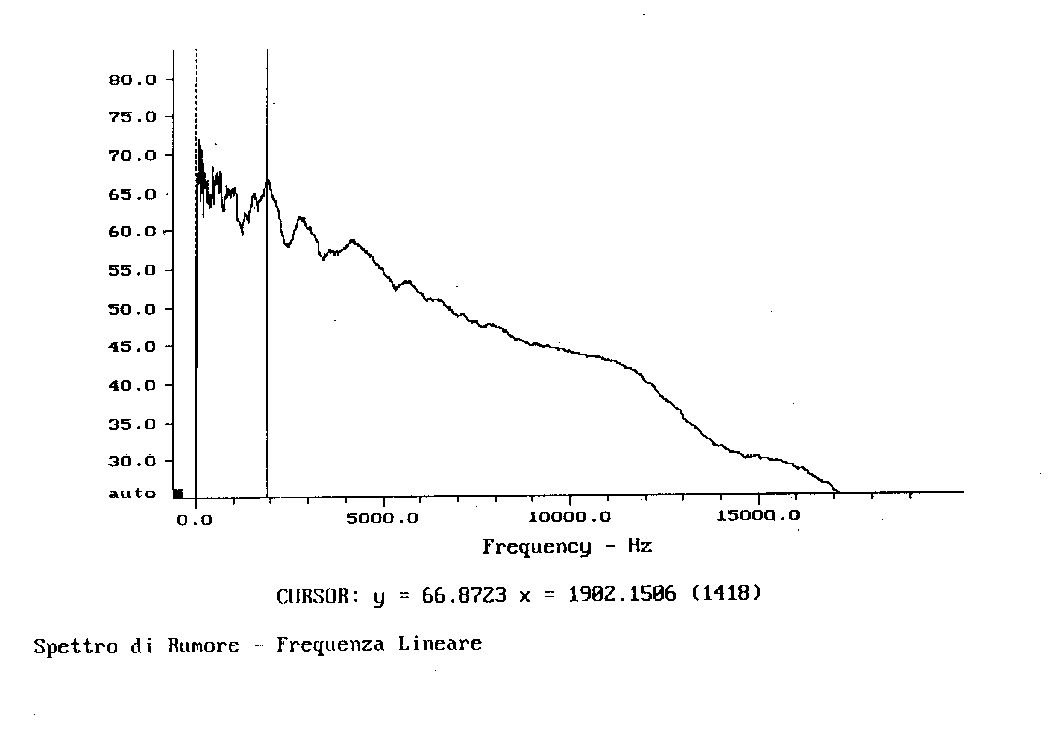
Figura 10 - Spettro in banda stretta con scala delle frequenze lineare -
E’ importante notare che per quanto riguarda l’udito la rappresnetazione che più ci si avvicina è quella a terzi d’ottava logaritmica, in quanto il nostro sistema sensoriale ha larghezze di banda che variano approssimativamente in maniera logaritmica. Un altro motivo per cui è preferibile l’analisi a banda percentuale costante è che per rappresentarla occorrono solamente 30 valori, mentre in quella a banda stretta ne servono decine di migliaia, questo però da luogo ad una perdita di informazione, infatti vengono scartati completamente i valori di fase e maggiorparte di quelli d’ampiezza, impedendoci di ritornare al suono di partenza, cosa che invece riusciamo a fare facilmente attraverso l’analisi in banda stretta applicando l’antitrasformata di Fourier.
5-Campionamento
Per campionamento di un suono s’intende l’individuazione di un intervallo di tempo DT e il successivo prelevamento dei valori del segnale in istanti multipli di DT.
Il periodo di campionamento più utilizzato è DT=22,676 ms da cui deriva una frequenza di campionamento fc= 44100 Hz; se campioniamo quindi un segnale con periodo pari ad un secondo, estrapoleremo ben 44100 valori/secondo, se in fine lo sottoponiamo ad un’operazione di DFT, produrremo un numero di componenti frequenziali pari alla metà del numero di valori campionati +1 (il +1 indica la componente continua o valore medio del segnale).
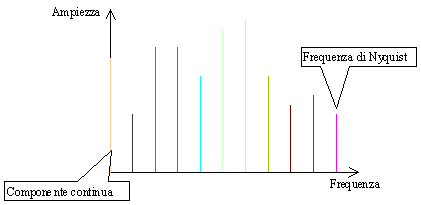
Figura 11
La frequenza massima è detta "frequenza di Nyquist" e corrisponde alla metà della frequenza di campionamento(fC). La risoluzione del campionamento è definita in questo modo:
![]() (13
(13
Il valore minimo della frequenza di campionamento è definita dal:
TEOREMA DI SHANNON
"La frequenza di campionamento deve essere maggiore o uguale al doppio della frequenza massima contenuta nel segnale". Se non rispetto questo teorema le componenti di suono a frequenza più elevate saranno sottocampionate e appariranno a frequenze più basse(fenomeno chiamato ALIASING).
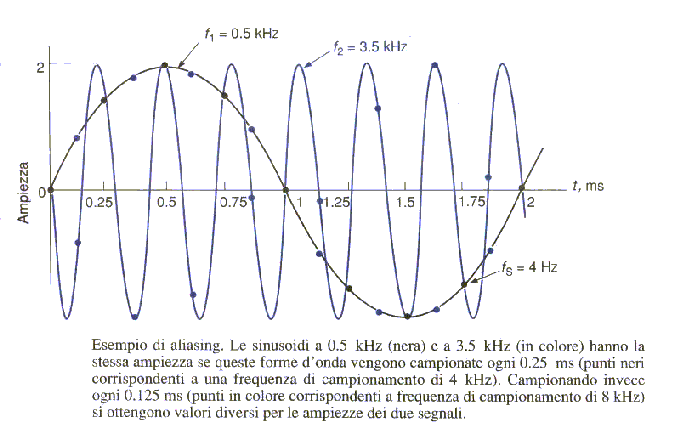
Figura 12 - Segnale sottocampiomato -
Più aumentiamo la frequenza di campionamento, maggiore sarà il numero di valori nell’unità di tempo e quindi minore sarà l’errore che commetterò; per questo motivo in pochi anni le frequenze di campionamento sono aumentate notevolmente:
|
Dispositivo |
Frequenza di campionamento ( Hz ) |
|
CD – Compact Disc |
44100 |
|
DAT – Digital Audio Tape |
48000 |
|
DVD – Digital Video Disc |
96000 |
|
DVD Audio |
192000 |
L’utilità di frequenze di campionamento così elevate( 192 KHz , 96 KHz ) è discutibile almeno per quanto riguarda l'utilizzo acustico, perché il nostro sistema uditivo non è così sensibile.
Un sistema di campionamento classico è fatto così:
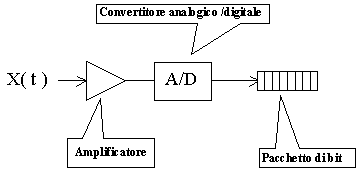
Figura 13 - Campionatore -
Il segnale analogico viene mandato ad un convertitore analogico/digitale che campiona il segnale e lo trasforma in parole di n bit. Il campionamento attraverso un A/D provoca un’ulteriore perdita d’informazione: infatti, sul segnale si opera un’altra discretizzazione oltre a quella nel tempo, vale a dire quella d'ampiezza. Per codificare gli infiniti valori possibili di un segnale analogico bisognerebbe avere a disposizione un numero infinito di bit. Questo, ovviamente, non è possibile e quindi si limita la lunghezza delle parole di bit e di conseguenza il numero dei livelli d’ampiezza assumibili dai campioni.
Una caratteristica che deve essere garantita nel campionamento, è un alto rapporto SEGNALE-RUMORE (S/N), che è controllabile attraverso il numero di bit utilizzati.
Storicamente parlando, si è partiti da sistemi a 16 bit come il CD (65536 diversi valori di ampiezza), si è poi passati da sistemi di fascia media come DAT o DVD che hanno dai 20 a 24 bit fino ad arrivare ai sistemi più moderni vale a dire i DVD-A a 24 bit che garantisce un rapporto S/N di circa 160 dB.
6-Filtri numerici
Avendo a disposizione un circuito campionatore come quello in figura 13 (per esempio una scheda audio da PC), per emulare la risposta di un filtro d’ottava o a frazioni di quest’ultima utilizzeremo un FILTRO NUMERICO.
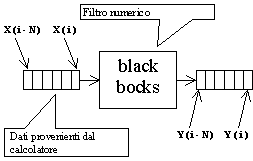
Figura 14 - Filtro numerico -
I dati in ingresso vengono elaborati da una formula matematica che produce in uscita dei nuovi valori:
![]() (14
(14
questa è la risposta di una struttura chiamata FIR vale a dire un filtro a risposta all’impulso finita; viene detta "RISPOSTA ALL’IMPULSO" o "FUNZIONE DI TRASFERIMENTO" la risposta del sistema alla "SEQUENZA DI DIRAC" o "IMPULSO DI DIRAC"
![]()
Figura 15 - Funzione di trasferimento
![]()
Figura 16 - Sequenza di Dirac
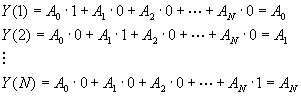 (15
(15
Questo filtro viene detto FIR in quanto sotto l’eccitazione dell’impulso di Dirac ha una risposta formata solamente da un numero limitato di campioni non nulli. Questo tipo di filtro è "poco potente", ma è STABILE, cioè non si mette mai ad oscillare e attraverso di esso riusciamo ad applicare qualunque tipo di filtraggio al segnale purché N sia sufficientemente grande.
Attraverso strutture di tipo FIR, tarando opportunamente i coefficienti A0,A1,…….,AN, si riesce ad emulare la risposta a filtri d’ottava o di 1/3 d’ottava rimanendo entro le tolleranze fissate dal IEC.
I filtri numerici più utilizzati sono quelli di tipo IIR o FILTRI RICORSIVI che utilizzano una struttura un po’ più complessa di quelli visti fino ad ora, in quanto l’uscita dipende anche dalla storia del filtro:
![]()
![]() (16
(16
solitamente con ![]()
Strutture di questo tipo hanno una risposta all’impulso infinita, vale a dire che eccitando il filtro con una sequenza di Dirac l’uscita non andrà mai a zero, anche se però vi tenderà e quindi ai fini pratici si potrà utilizzare come un FIR. Con una struttura di tipo IIR occorre fare molta attenzione all’instabilità che si potrebbe verificare qualora i coefficienti Bi fossero molto grandi, in quanto questo comporterebbe l’autoalimentazione del filtro con segnali sempre più forti.
I filtri di questo tipo sono i più utilizzati perché con un ridotto numero di campioni produce un filtraggio migliore di quelli prodotti dai FIR; tarando opportunamente i coefficienti Ai e Bi, otterremo un filtro stabile che soddisfa le maschere di tolleranza previste dalla IEC.
7 - Analisi di un segnale campionato
Focalizziamo l'attenzione sull'analisi di segnali transienti.
L'analisi di questo tipo di suono non è un problema per i dispositivi analogici tipo l’analizzatore di segnali transienti in figura 4, fermo restando che si riesca a memorizzare i dati abbastanza velocemente. Visualizzando tutti i valori ricavati otterremo un MULTISPETTRO, cioè un insieme di spettri nel tempo.
La trasformata di Fourier non si presterebbe allo studio di suoni transienti: infatti non è detto che questi ultimi siano periodici. Vedremo però che utilizzando qualche artifizio questo diventa possibile.
Un problema da risolvere è quello della continuità del segnale: infatti, analizzando una porzione di segnale formato da N campioni, può capitare che i valori d’inizio e di fine finestra non coincidano. Prendiamo per esempio una sinusoide e analizziamone una porzione differente dal suo periodo:
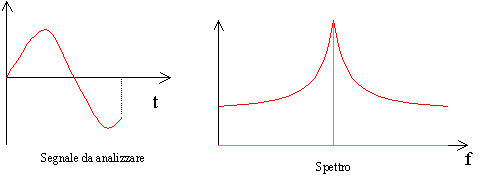
Figura 17
Lo spettro risultante è la campana di colore rosso, mentre ci aspettavamo un’unica riga verticale (in azzurro), questo succede perché la trasformata suppone periodico il segnale e quindi vengono a formarsi dei gradini aventi un contenuto frequenziale molto elevato: questo fatto è detto FENOMENO DI LEAKING.
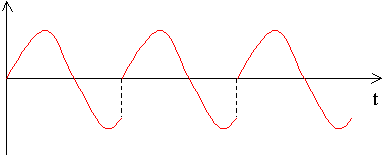
Figura 18
La scelta del numero di punti da studiare (quindi la porzione di segnale) non è libera in quanto il calcolo della trasformata ristretta di Fourier è molto rapido solo se il numero di valori da studiare è multiplo di due: quindi, per fare in modo che il segnale sia continuo, lo si forza ad andare a zero applicando una sorta di filtro di copertura, vale a dire si moltiplica ogni valore campionato per una funzione detta window (finestra) di durata pari al segmento di segnale da studiare (N valori campionati):
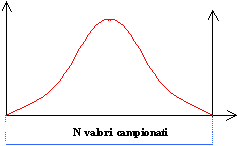
Figura 19 - Window -
Se moltiplichiamo ogni periodo del segnale di figura 18 per questa funzione, i suoi estremi sono forzati a zero mentre i valori dei punti al centro della finestra mantengono il loro valore iniziale. Questa operazione ha però un inconveniente, cioè quello che i valori campionati vengono presi in considerazione con pesi diversi; per ovviare a questa imperfezione si fa scorrere la finestra non di N campioni, ma di N/2: così facendo ogni punto sarà elaborato con una somma dei pesi sempre pari a 1.
Esistono vari tipi di finestre indicate qui sotto:
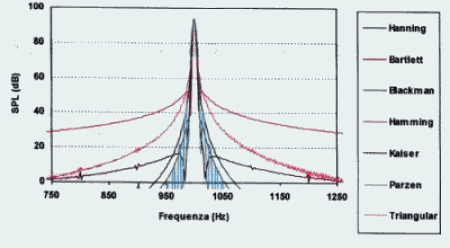
Figura 20 - Spettro di un segnale sinusoidale sottoposto a varie funzioni -
Quella più conveniente sembrerebbe la Hanning, in quando da luogo ad uno spettro abbastanza stretto e senza bande laterali "strane" come è invece succede per la Hamming(due bande laterali).
La funzione di tipo Hanning consiste in un "coseno quadro rialzato":
![]()
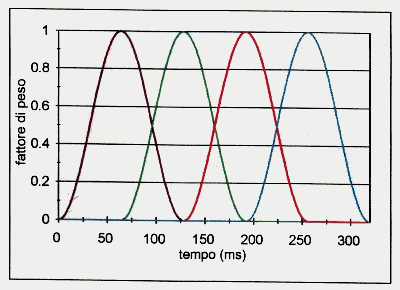
Figura 21 - Hanning traslato di N/2 -
Quando si utilizzavano campionatori da 10 o 12 bit bande laterali da -70 dB non davano fastidio, mentre ora con convertitori a 24 bit e un rapporto segnale-rumore di 120![]() 130 dB questi lobi laterali non sono accettabili.
130 dB questi lobi laterali non sono accettabili.
Con questa tecnica si ottengono due tipi di multispettro:
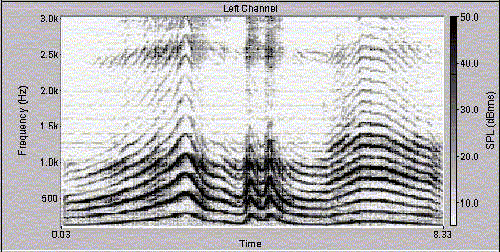
Figura 22 - Sonogramma -
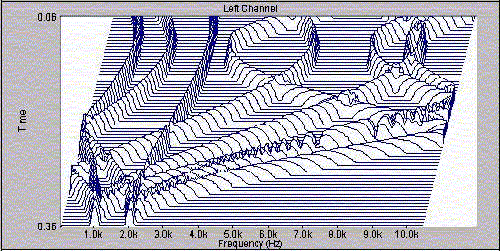
Figura 23 - Multispettro di tipo Waterfall -