Clara PATINI matr. n. 119156 – Lezione del 09.11.99 ore 16.30 – 18.30
LE PERDITE DI CARICO
Argomenti trattati nella lezione:
In un tubo in cui scorre un fluido le perdite di carico corrispondono alle perdite di pressione: per calcolarle si può utilizzare l’equazione che esprime la velocità in funzione della variazione di pressione (1).
![]()
(1)
in cui w e m sono rispettivamente la velocità media e la viscosità del fluido, L ed R la lunghezza del condotto e il raggio della sua sezione.
La perdita di carico è quindi direttamente proporzionale alla viscosità e alla velocità del fluido e alla lunghezza del tubo ed è inversamente proporzionale al quadrato del raggio della sezione. Ad ogni metro di tubo corrisponde quindi una certa perdita di carico; inoltre, più il fluido scorre veloce, più energia viene dissipata.
Poiché le perdite di carico risultano proporzionali alla lunghezza del condotto, si considerano distribuite lungo il condotto stesso e per questo vengono definite perdite distribuite.
La perdita di carico può anche essere espressa in funzione del numero di Reynolds, la cui espressione è
![]()
in cui r è la densità del fluido e D il diametro della sezione del tubo.
Si consideri infatti la relazione (1): moltiplicandola e dividendola per la velocità media w, per la densità r e sostituendo il raggio R con il diametro D, si ottiene:
![]()
(2)
L/D è un rapporto adimensionale e w2 /D è l’energia cinetica a meno del fattore a.
Il numero puro 64/Re prende il nome di fattore di attrito e viene indicato, a seconda dei testi, con le lettere f, x o l. Tali differenze nella nomenclatura dipendono dal fatto che il moto dei fluidi è un argomento al confine tra tre settori scientifici diversi: la fisica tecnica (disciplina appartenente alle scienze termiche), l’idraulica (disciplina appartenente all’ingegneria civile) e l’aerodinamica (disciplina appartenente all’ingegneria meccanica e aeronautica).
A volte, nella termofluidodinamica, viene usato anche un altro fattore, Cf, pari a
![]()
In questa trattazione, seguendo la scuola tradizionale della fisica tecnica, si utilizzerà il fattore di attrito e lo si indicherà con la lettera x. L’espressione della perdita di carico risulta allora
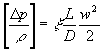
(3)
Tale espressione non ha però validità generale: è esatta solo nel caso particolare di regime laminare completamente sviluppato, con tubo di sezione circolare e superficie liscia, quando cioè è valida la soluzione parabolica di Poiseuille. Il fattore di attrito non è una costante: in tutti gli altri casi x assume un valore diverso da 64/Re.. Il fattore di attrito è definito come quel numero puro che rende vera la relazione (3) e il suo valore, che viene ricavato sperimentalmente, dipende principalmente da tre fattori:
I valori del fattore di attrito inteso come funzione del numero di Reynolds e della rugosità relativa sono tabulati. Questa funzione viene anche rappresentata graficamente tramite un diagramma. Tale diagramma venne realizzato pressoché contemporaneamente da studiosi di fluidodinamica, di idraulica e di aerodinamica ed è conosciuto come diagramma di Moody (fig. 1) o, in idraulica, arpa di Nikuradse, per la forma caratteristica.
Il diagramma, che è realizzato in scala doppio logaritmica, riporta in ascissa il numero di Reynolds e in ordinata il fattore di attrito.
Nelle ipotesi di regime laminare completamente sviluppato con tubo di sezione circolare e superficie liscia la curva è un’iperbole equilatera.
Nel caso generale si suddivide il diagramma in tre zone distinte.
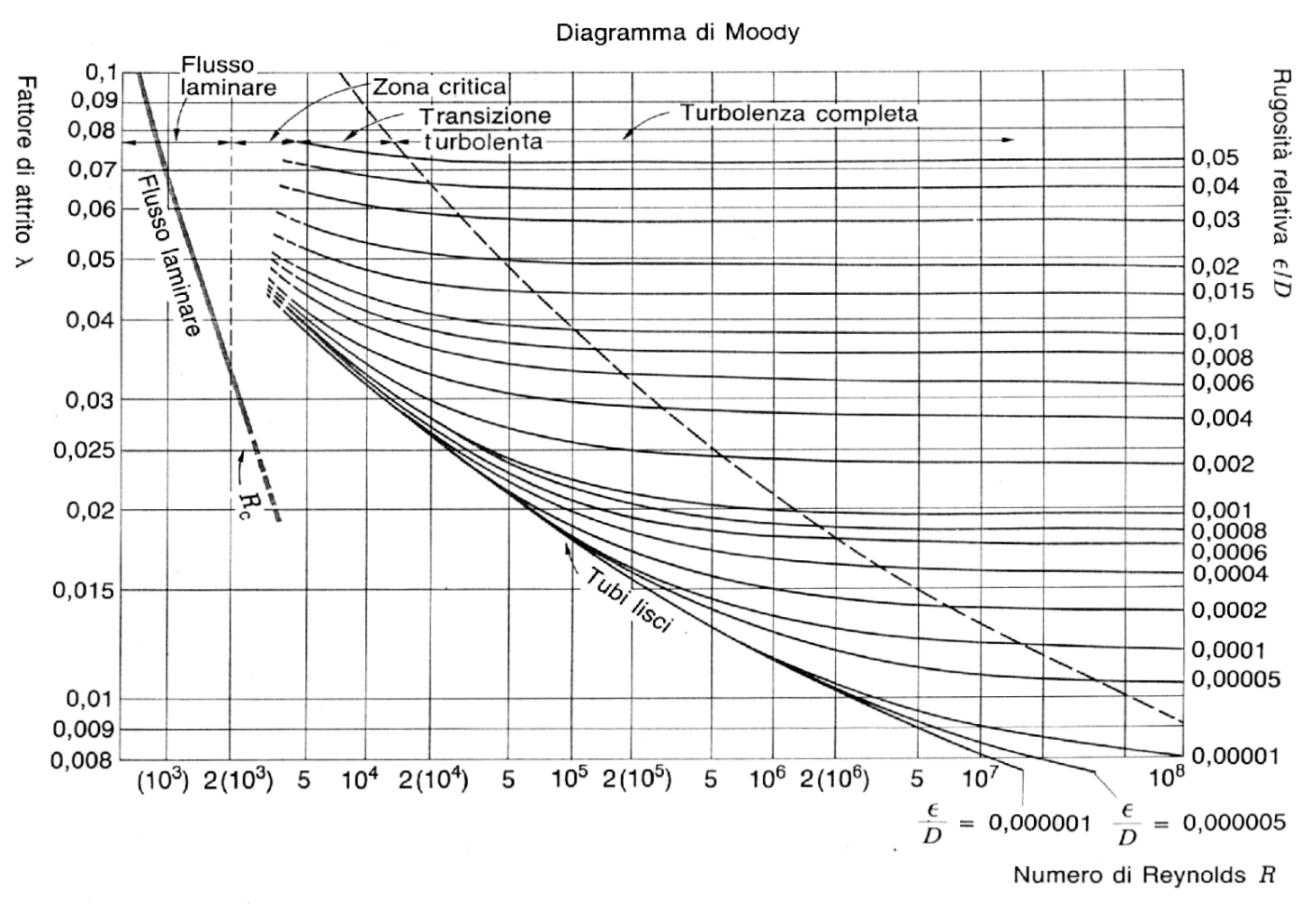
(fig. 1)
|
materiale |
e (mm) |
|
acciaio chiodato |
0.0 – 9.0 |
|
cemento |
0.3 – 3.0 |
|
doghe in legno |
0.19 – 0.9 |
|
fusione in ferro |
0.25 |
|
ferro zincato |
0.15 |
|
ferro asfaltato |
0.12 |
|
acciaio commerciale |
0.046 |
(tab. 1)
Al diagramma di Moody viene generalmente allegata una tabella (tab. 1) che riporta i valori della scabrezza per i materiali con cui tipicamente si realizzano i tubi per il trasporto dell’acqua.
Ad eccezione del tratto in cui la curva assume l’andamento simile a quello di una retta orizzontale, in cui vale la relazione
![]()
(4)
il diagramma di Moody non consente di risolvere i problemi in forma chiusa. Il fattore di attrito infatti è noto solo se è noto il numero di Reynolds. Ma se il numero di Reynolds è un’incognita, cioè il problema è a velocità non assegnata, si deve procedere nella risoluzione per tentativi. Si ipotizza una velocità, che viene detta di tentativo, si determina mediante il diagramma di Moody il fattore di attrito corrispondente e si ricava in funzione di esso, mediante l’equazione (3), una nuova velocità, sicuramente diversa da quella di tentativo. A partire dalla nuova velocità si ripetono le stesse operazione iterativamente finché il risultato non si stabilizza.
I risultati ottenuti vengono utilizzati nella pratica per risolvere diversi tipi di problemi.
PROBLEMA
Si calcoli la perdita di carico di un tubo di sezione circolare avente un diametro interno D di 2 in, una lunghezza L di 75 ft, nel quale scorre ammoniaca (NH3) satura alla temperatura T di 10 °F e con una velocità media w di 70 ft.s-1. La scabrezza e del condotto sia pari a 0.00015 ft, la viscosità dell’ammoniaca m 5.78 10-6 lb.ft-1s-1 e la sua densità r 0.137 lb.ft3.
Soluzione
Convertendo i dati nel sistema internazionale, considerando che
1 in = 2.540 × 10-2 m
1 ft = 0.3048 m
1 lb = 0.4536 kg
1 lb.ft-3 = 16.02 kg.m-3
e che la relazione tra le scale Celsius (C) e Fahrenheit (F) è
TF = 9/5 TC + 32
si ottengono i seguenti dati:
D = 50.8 mm
L = 22.86 m
T = -12.2 °C
w = 21.3 m.s-1
e
= 0.046 mmm = 8.6 × 10-6
kg.m-1× s-1 = 8.6 × 10-6 Pa× sr
= 2.19 kg.m-3Per calcolare la perdita di carico nel tubo si usa la relazione (3):
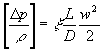
Il valore del coefficiente di attrito x è funzione del numero di Reynolds Re e della rugosità relativa e/D.
![]()
Tale valore di Re è piuttosto elevato e pertanto il regime sarà fortemente turbolento.
![]()
Con questi valori si può leggere sul diagramma di Moody che il fattore di attrito x è:
x =
0.0205Dalla (3) si ricava allora che
![]()
Nell’esercizio precedente la perdita di carico è stata espressa in Pascal poiché sono state usate le unità di misura del sistema internazionale. Ma in idraulica tradizionalmente le perdite di carico vengono espresse in metri di colonna d’acqua. Infatti tale scienza definisce il carico come la grandezza fisica che esprime, in metri di colonna d’acqua, la pressione esercitata dall’acqua stessa.
Per convertire i metri di colonna d’acqua in Pascal, e cioè per passare da una misura lineare in altezza alla corrispondente misura di pressione, si utilizza la legge di Stevino. Secondo tale legge, che regola la statica dei fluidi e cioè è valida se il fluido è in equilibrio, se si considera la pressione agente sul pelo libero nulla, la pressione a una quota generica del fluido x è p = r× g× x, in cui g è l’accelerazione di gravità.
Se si considera l’acqua, che ha una densità r di 1000 kg.m-3, approssimando l’accelerazione di gravità g a 10 m.s-2 (vale 9.81 m.s-2), si ottiene la relazione 1 bar = 10 m, che è assolutamente scorretta in termini dimensionali, ma in idraulica viene assunta come equivalenza.
Non si deve però cadere nell’errore di considerare carico e pressione equivalenti quando il fluido è in moto. Si esamini infatti il seguente problema.
PROBLEMA
Dato un serbatoio aperto, contenente acqua, dotato nella base di un tubo da cui l’acqua fuoriesce, si determini la pressione nel punto in cui il tubo termina, considerando che questo si trova ad una distanza H di 20 metri dal pelo libero dell’acqua.
Soluzione
Sia 1 un punto sul pelo libero dell'acqua e 2 il punto in cui il tubo termina. Poiché l’acqua è in moto non si può applicare la legge di Stevino e concludere che la pressione in 2 è
p2 = r× g× H = 2 bar.
Nonostante il dislivello, la pressione in 2 è uguale alla pressione in 1: la differenza di pressione è nulla perché è stata assorbita dalle perdite di carico.
Bisogna quindi semplicemente concludere che la pressione in 2 è, come in 1, la pressione atmosferica, che in idraulica, aerodinamica e fluidodinamica si assume pari a zero. Quindi
p1 = 0, p2 = 0.
In realtà la pressione atmosferica è pari a 1 bar, ma queste scienze, basandosi sul fatto che è sempre presente, la considerano inesistente, cioè nulla, e riportano ad essa le altre pressioni che per questo vengono dette relative. I manometri sono volutamente tarati perché la misura della pressione atmosferica sia zero. Tale ragionamento non è però pienamente giustificabile in quanto la pressione atmosferica non è una costante fisica, ma varia, ad esempio al variare dell’altitudine (in montagna la pressione atmosferica è significativamente più bassa di quella che si ha al livello del mare).
Le perdite di carico distribuite non sono le uniche cause di cadute di pressione nei condotti idraulici. Esistono infatti anche le perdite di carico dette concentrate o localizzate. Esse sono dovute agli ostacoli come, ad esempio curve, gomiti, valvole, brusche variazioni di pressione, che il fluido può incontrare mentre scorre all’interno del tubo. La figura seguente (fig. 2) mostra alcune tipiche cause di perdite di carico concentrate.
Sono schematizzati uno spigolo vivo ed una curva ben raccordata (che danno una perdita di carico diversa), un rubinetto (la perdita di carico dipende da quanto il rubinetto è aperto ed è comunque non nulla anche se questo è completamente aperto), una diramazione che termina con un rubinetto (c’è perdita di carico anche se il rubinetto è chiuso), un tubo la cui sezione si allarga in un caso e si restringe nell’altro in modo brusco e dolce.
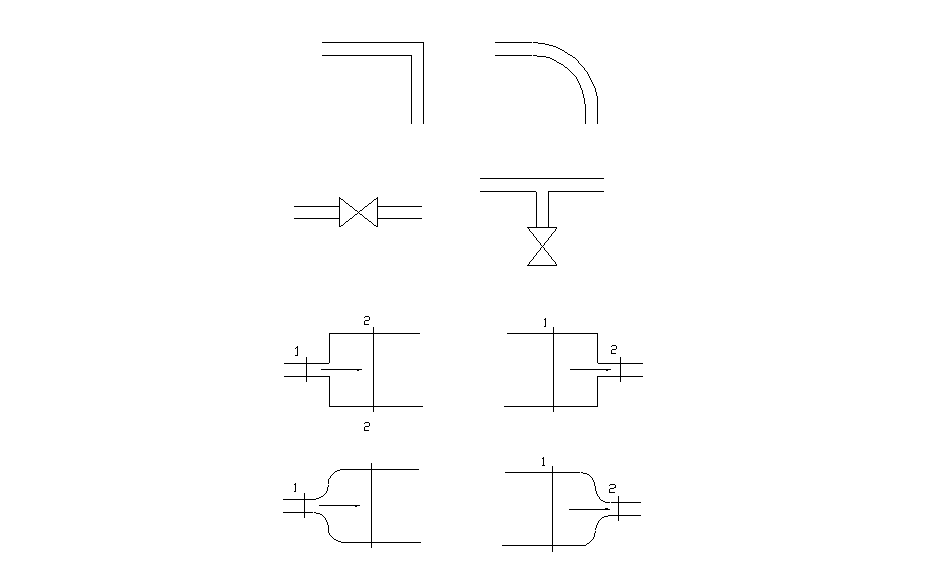
(fig. 2)
Le perdite di carico concentrate hanno un’espressione coerente con quella delle perdite di carico distribuite. Ma a differenza di queste ultime, le perdite di carico concentrate non dipendono dalla lunghezza del tubo (scompare il termine L/D), in quanto sono localizzate (concentrate) in un ben determinato punto. Indicando con b il fattore di attrito, l’espressione delle perdite di carico concentrate è:
![]()
(5)
in cui w e r sono rispettivamente la velocità media e la densità del fluido. E’ necessario però prestare attenzione alla velocità che si considera. Infatti se la sezione del tubo ha diametro costante anche la velocità è costante, ma se il diametro varia, come negli ultimi casi della figura 2, la velocità in ingresso w1 è diversa da quella in uscita w2. Per l’equazione di continuità introdotta nello studio dei sistemi aperti in regime stazionario la portata in massa che entra nella sezione 1 è uguale alla portata in massa che esce dalla sezione 2, e cioè
![]()
Ma poiché questa relazione si può scrivere anche nella forma
r
w1 S1 = r w2 S2dove S è la sezione del tubo, si deduce subito che se la sezione si allarga la velocità diminuisce, mentre se la sezione si restringe la velocità aumenta.
Tutto ciò è valido se si ipotizza la densità r del fluido costante. Infatti la relazione di proporzionalità diretta tra velocità del fluido e sezione del tubo può non essere valida se si considera che al variare della pressione può variare anche il volume specifico del fluido e quindi la sua densità. Considerare r costante è nella maggior pare dei casi un’approssimazione ragionevole (per esempio si può considerare costante la densità dell’aria che circola nei tubi di un impianto di ventilazione, in cui la variazione di pressione complessiva è trascurabile rispetto la pressione atmosferica, mentre non si può considerare costante la densità di un gas che, passando attraverso un ugello, viene portato dalla pressione di 1 bar a quella di 50 bar).
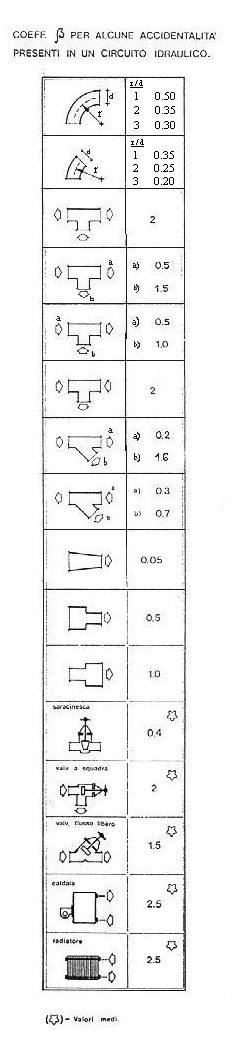
(fig. 3)
I valori del fattore di attrito b per i casi più comuni sono riportati in tabelle. Nella tabella di figura 3 si può ad esempio leggere che b può variare tra 0.3 e 0.5 in una curva a gomito ben raccordata, vale 2 per una diramazione a T, 0.5 se il tubo si allarga e 1.5 se il tubo si restringe (diversamente da quanto si potrebbe pensare si ha una perdita maggiore allargando il tubo piuttosto che strozzandolo), vale 0.4 per una valvola a saracinesca, 2 per una valvola a squadra aperta, 2.5 per una caldaia. Si può così ad esempio determinare la pompa che occorre per mantenere in circolazione l’acqua in un impianto di riscaldamento. Infatti la somma delle perdite di carico distribuite e concentrate in tutto l’impianto deve essere bilanciata dal salto di pressione prodotto dalla pompa: in un impianto di 300-500 metri in cui le perdite di carico sono pari a 4.5 bar sarà necessaria una pompa da 5 bar.
L’espressione delle perdite di carico distribuite (3) non è corretta se si considerano tubi di sezione non circolare. Se la sezione del tubo non è circolare nella relazione (3) si deve sostituire il diametro D con il cosiddetto diametro idraulico equivalente (DEQ), che viene definito
![]()
con A e p pari rispettivamente all’area ed al perimetro della sezione.
Nel caso di tubo a sezione circolare di diametro D si ha
![]()
![]()
e quindi, come deve essere,
![]() .
.
Ma nel caso di tubo a sezione quadrata di lato l si ha
![]()
![]()
e quindi
![]() .
.
Ma il calcolo del diametro equivalente non è sempre così semplice. Esistono per questo tabelle (tab. 2) che riportano il valore del diametro equivalente di tubi con sezione particolare. La tabella 2 riporta inoltre il numero da sostituire a 64 nell’espressione per il calcolo del fattore di attrito x=64/Re a seconda della forma della sezione del tubo. Il fattore di attrito ad esempio è x=57/Re per un tubo di sezione quadrata (è un valore non molto diverso da x=64/Re, se si considera che gli errori che si commettono in questo regime di moto dei fluidi sono normalmente del 30%) , x=53/Re per un tubo di sezione triangolare, x=96/Re per un tubo di sezione anulare.
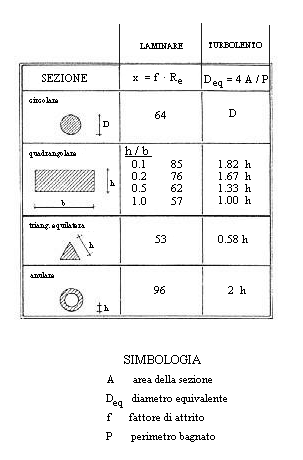
(tab. 2)
Per calcolare la perdita di carico totale, anziché sommare alle perdite di carico distribuite le perdite di carico concentrate, si può procedere con un metodo alternativo. Questo consiste nell’utilizzare direttamente la formula (3), con la sola accortezza di maggiorare la lunghezza del condotto sostituendo L con L+LEQ , dove LEQ è la somma delle lunghezze equivalenti di tutte le accidentalità.
Per determinare una lunghezza equivalente si usa un nomogramma (fig. 4).
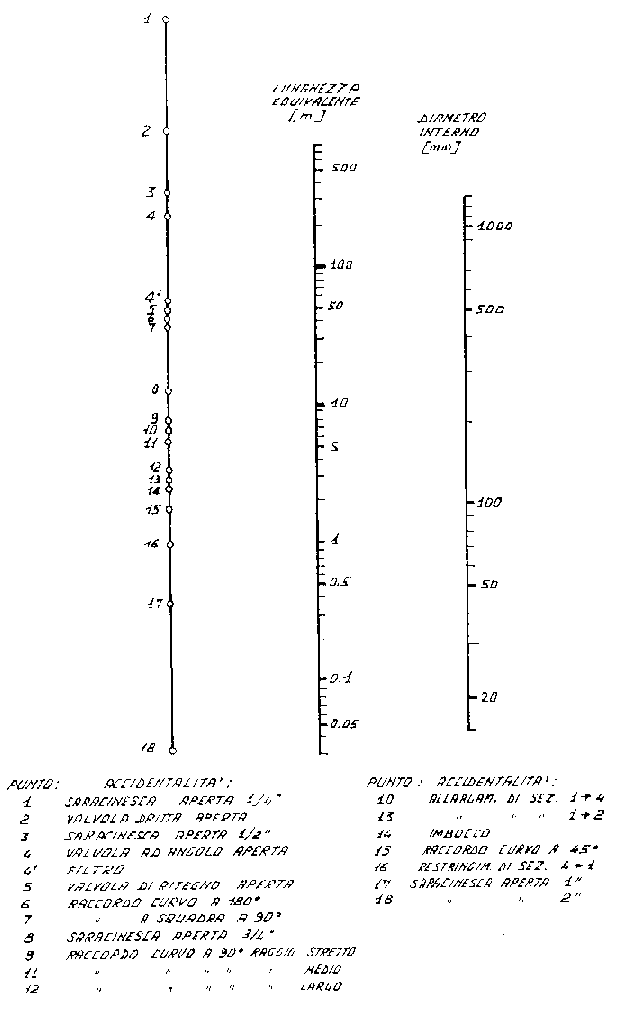
(fig. 4)
Tale diagramma è costituito da tre assi verticali paralleli: su quello a destra vengono riportati i valori del diametro interno della sezione del tubo in millimetri, su quello a sinistra valori corrispondenti alle accidentalità del tubo e su quello centrale i valori della lunghezza equivalente in metri. Conoscendo il diametro interno del tubo e il tipo di accidentalità si può ricavare il valore della lunghezza equivalente semplicemente congiungendo con una retta i due punti sugli assi esterni corrispondenti ai valori noti: la lunghezza equivalente è pari al valore in metri corrispondente al punto in cui tale retta interseca l’asse centrale.
Per esempio la lunghezza equivalente di un tubo avente diametro interno pari a 100 mm con una valvola ad angolo aperta (corrisponde al punto 4) è circa 20 m, mentre la lunghezza equivalente di un tubo dello stesso diametro interno che ha un restringimento di sezione da 4 ad 1 (punto 16) è poco più di 1 m.