
ANALISI IN FREQUENZA
Lo scopo dell’analisi in frequenza è quello di definire il contenuto di un suono complesso, che contiene quindi componenti a diverse frequenze, anche variabili istante per istante.
Ricordando che il campo sonoro udibile umano va da 20 Hz a 20 kHz (circa) ma che l’orecchio non percepisce tutte le frequenze allo stesso modo, si capisce come mai in molte applicazioni tecniche che vanno dalla registrazione e riproduzione della musica, all’analisi del rumore prodotto da macchinari, allo studio della risposta sonora di ambienti, ecc. si è interessati a valutare non tanto il livello sonoro complessivo, cioè l’energia totale del suono, bensì la sua distribuzione alle varie frequenze.
Per effettuare l’analisi in frequenza si tratta quindi di partire da una rappresentazione del suono nel dominio del tempo, la forma d’onda, ed arrivare a definire lo spettro, cioè un diagramma cartesiano che riporta sull’asse delle ascisse le frequenze in Hz e su quello delle ordinate i corrispondenti livelli in db (fig. 1). La forma d’onda è in sostanza un grafico che visualizza l’andamento di un segnale elettrico generato da un microfono, il quale si basa di solito sulla variazione della pressione nel mezzo in cui è "immerso".

Figura 1
Uno stesso segnale si può comunque rappresentare con spettri di diverso tipo.
Bisogna precisare che le conversioni dal dominio del tempo nello spettro sono sempre imprecise: non esiste, a tutt’oggi, un’apparecchiatura in grado di riprodurre fedelmente i fenomeni di analisi in frequenza che avvengono nel nostro orecchio, che rimane quindi un apparato migliore di qualunque macchinario realizzato finora. L’analisi in frequenza dà perciò spazio ad applicazioni di elaborazione di segnali uditivi ancora da scoprire.
Se il segnale è stazionario (costante nel tempo) l’analisi in frequenza è facile da realizzare: si può analizzare una frequenza alla volta e non si presentano problemi. Lo studio verrà allora diviso in due parti: una dedicata all’analisi dei segnali stazionari e una a quella dei transienti. E’ in quest’ultimo caso che la "macchina" non riesce ad eguagliare l’orecchio umano: ciò spiega come mai i programmi di riconoscimento vocale siano poco efficienti (la voce umana è ovviamente transiente).
Segnali stazionari
Filtri d’ottava
Un primo metodo usato per l’analisi in frequenza dei segnali stazionari si serve di un "banco" di filtri passa – banda (come i filtri d’ottava), cioè di una serie di dispositivi ciascuno dei quali lascia passare solo un determinato campo di frequenze, reiettando le componenti del suono a frequenze maggiori e minori. Collegando uno strumento di misura all’uscita di ogni filtro è possibile misurare il livello di segnale che compete al particolare intervallo di frequenze (fig. 2).
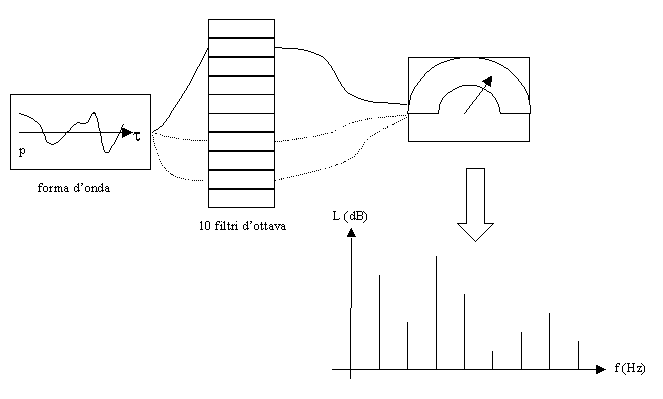
Figura 2
In un grafico in funzione della frequenza un filtro passa - banda si può rappresentare con una zona in cui il guadagno è pressoché costante e pari a 0 db (banda efficace, D f) e con due zone, ai lati della prima, in cui il guadagno decresce fino a valori trascurabili (fig. 3). La banda efficace è compresa tra f1 e f2, che sono le frequenze di taglio, poste a metà energia rispetto alla banda passante; per definizione G(f1) = G(f2) = -3 db. fc è la frequenza di centro banda, tale che G(fc) = 0 db.
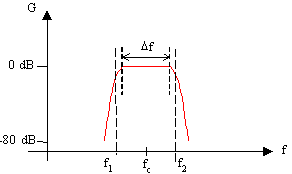
Figura 3
Bisogna notare che un filtro ideale dovrebbe avere la curva del guadagno fatta come un impulso rettangolare (in frequenza), ma finché il dispositivo è realizzato con componenti passivi i fronti di salita e di discesa non potranno mai essere verticali.
Ad es., se un filtro ha f1 = 707 Hz e f2 = 1414 Hz qualsiasi suono al di fuori di questo intervallo di frequenze non dovrebbe passare, ma in realtà queste componenti, anche se attenuate, si ritrovano ugualmente in uscita. La pendenza dei fronti di salita e discesa della caratteristica deve comunque essere contenuta all’interno di una tolleranza definita dall’IEC, un’organizzazione che si occupa della definizione degli standard per le misure acustiche.
Gli strumenti utilizzati per la lettura dei livelli sono in genere fonometri palmari con frequenze selezionabili successivamente: ad ogni scelta della frequenza si legge il valore indicato dallo strumento e lo si memorizza; al termine del procedimento si è in grado di definire lo spettro del segnale. Il suono deve ovviamente essere stazionario, altrimenti i livelli varierebbero nel tempo e la misura fatta in questo modo non avrebbe senso.
Per rendere il rilevamento sempre istantaneo è necessario un banco di voltmetri, che indica in tempo reale il segnale di uscita in forma analogica. Un dispositivo del genere è detto R.T.A. (Real Time Analyzer, analizzatore in tempo reale).
Un'ottava è definita come un intervallo di frequenze in cui il limite inferiore (f1) e quello superiore (f2) verificano le relazioni:
![]() (0)
(0)
Per coprire l’intero campo delle frequenze udibili ci vogliono 10 filtri d’ottava, ciascuno dei quali ha una frequenza di centro banda doppia di quella del filtro precedente (il tutto è disciplinato da norme I.S.O.):
fc1 |
fc2 |
fc3 |
fc4 |
fc5 |
fc6 |
fc7 |
fc8 |
fc9 |
fc10 |
31,5 Hz |
63 Hz |
125 Hz |
250 Hz |
500 Hz |
1 kHz |
2 kHz |
4 kHz |
8 kHz |
16 kHz |
Tabella 1
In molte applicazioni la suddivisione dell’asse delle frequenze in bande d’ottava risulta piuttosto grossolana, e vi è la necessità di usare filtri a banda più stretta (a frazione d’ottava), che mantengono però sempre la proporzione tra la larghezza di banda e la frequenza di centro banda:
![]() (1)
(1)
Per i filtri d'ottava la costante è pari a
![]() (2)
(2)
In questo modo f2 di un filtro è sempre uguale a f1 del successivo. Questi tipi di filtri sono detti ad apertura percentuale costante. Uno dei motivi che sta alla base dell’adozione di questo metodo è che il sistema uditivo umano risponde agli stimoli più secondo lo schema dell’apertura percentuale costante che secondo quello dell’apertura costante.
Ad es., per verificare la (1) deve essere:
Esistono quindi diversi tipi di filtri, a seconda del numero di parti in cui viene divisa ogni banda:
La scala dei terzi d’ottava è la più usata. E’ formata da 30 bande da 1/3 d’ottava ciascuna.
Esempio
Consideriamo il caso di un filtro in terzi d’ottava, e vediamo come risulta la suddivisione della banda d’ottava che ha fc=1000 Hz. Devo in pratica trovare fc1, fc2, fc3, f1, f2, f3 e f4, cioè le tre frequenze di centro banda e gli estremi di ogni banda (fig. 4).
Troviamo intanto la frequenza di taglio inferiore della banda d’ottava:
![]() (3)
(3)
Si ha anche che
![]() (4)
(4)
Le condizioni da verificare sono:
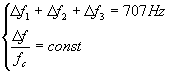 (5)
(5)
Ora definisco il rapporto tra due frequenze di centro banda consecutive:
![]() , con i=1,2,3. (6)
, con i=1,2,3. (6)
Elevando K al cubo (perché voglio bande da 1/3 d’ottava) ottengo tutta l’ottava, quindi un raddoppio della frequenza:
![]() (7)
(7)
Ricavo K:
![]() (8)
(8)
Considerando che la (6) vale anche per le freq. di taglio posso allora trovare:
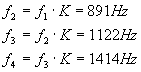 (9)
(9)
e anche:
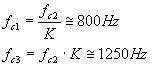 (10)
(10)
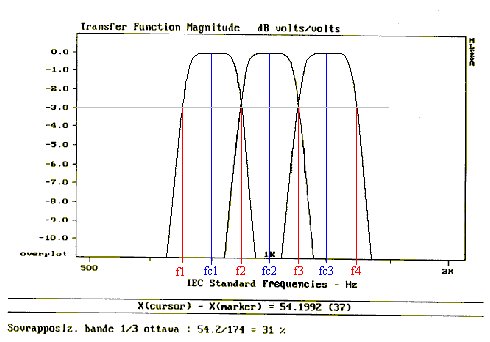
Figura 4
Dal grafico si vede che se la frequenza di un suono puro cade nella zona in cui due bande da 1/3 d’ottava si sovrappongono allora lo spettro ha energia in due diversi intervalli di frequenze. Questo fenomeno non è raro, perché la sovrapposizione è circa del 30%.
Osservazione
E’ importante osservare che uno spettro, a seconda della tecnica utilizzata per ricavarlo e del tipo di visualizzazione impiegato, può cambiare anche notevolmente d’aspetto. Se prendiamo ad esempio uno spettro in bande di 1/3 d’ottava con asse delle frequenze in scala lineare (fig. 5) e lo confrontiamo con uno in scala logaritmica (fig. 6), vediamo che il primo comprime in un breve intervallo di frequenze una notevole quantità di informazioni.
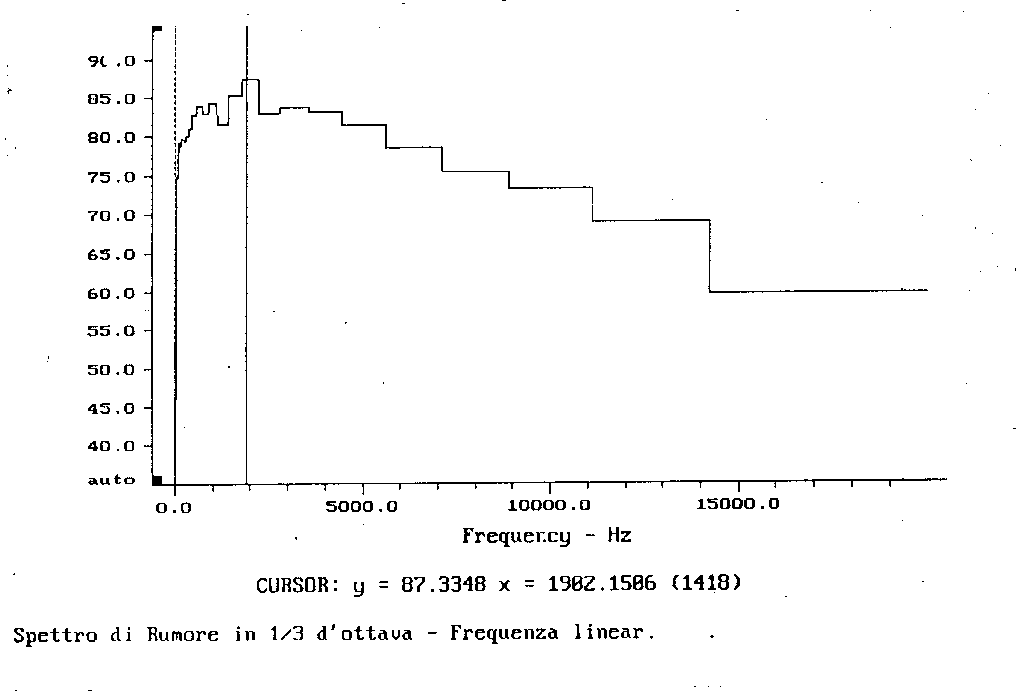
Figura 5
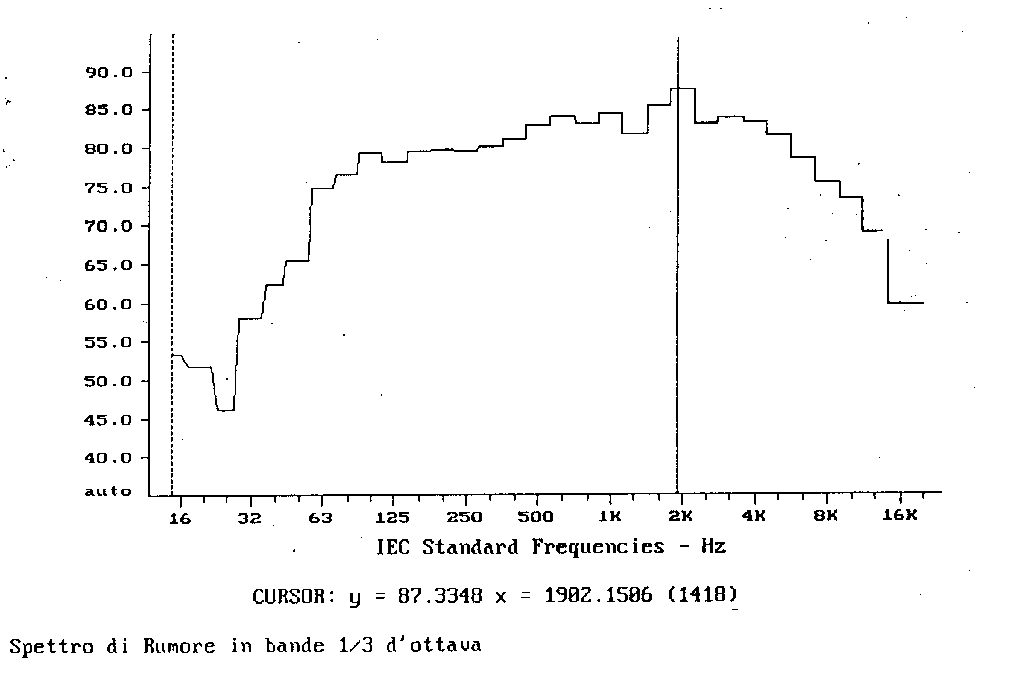
Figura 6
Le prossime due figure, che si riferiscono allo stesso suono dei due grafici precedenti, oltre a fornire un’ulteriore prova di quanto detto sopra, evidenziano anche un altro fenomeno. In fig. 7 è riportato lo spettro in banda stretta in scala logaritmica, in fig. 8 in scala lineare (sempre dell’asse delle ascisse).
Notando che la posizione del cursore è sempre la stessa (1902,15 Hz circa), leggendo il valore corrispondente (~66,9 db) e confrontandolo con quello in fig. 5 e fig. 6 (~87,3 db) ci si rende conto che il livello negli spettri in bande di 1/3 d’ottava è molto superiore a quello negli spettri in banda stretta.
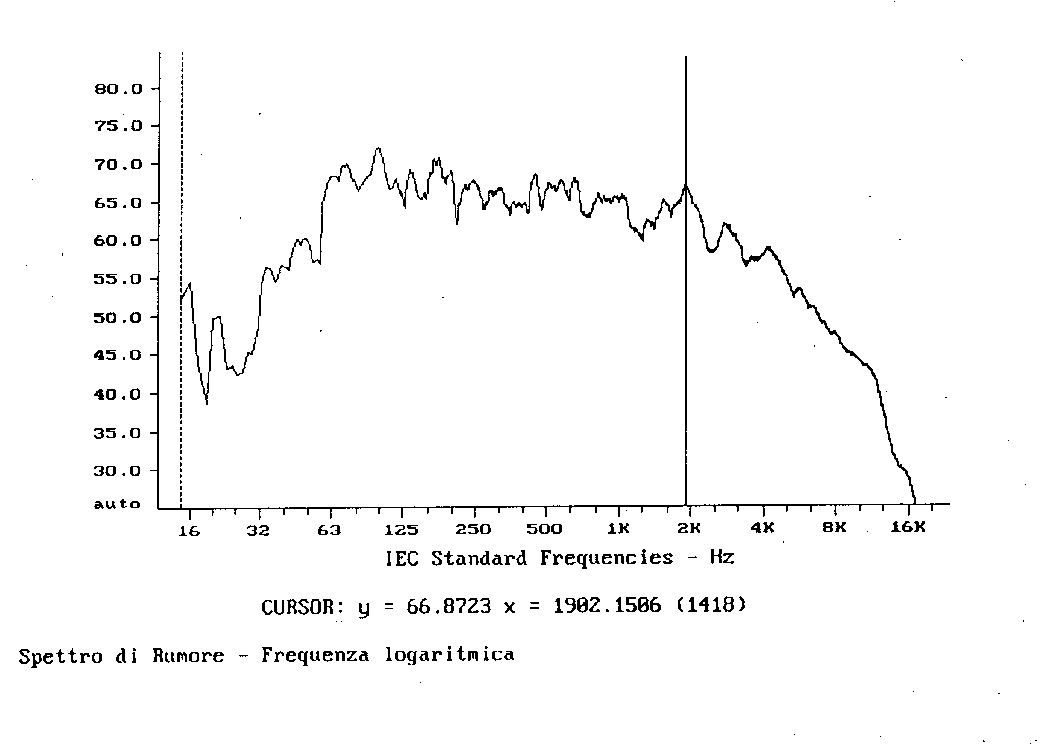
Figura 7
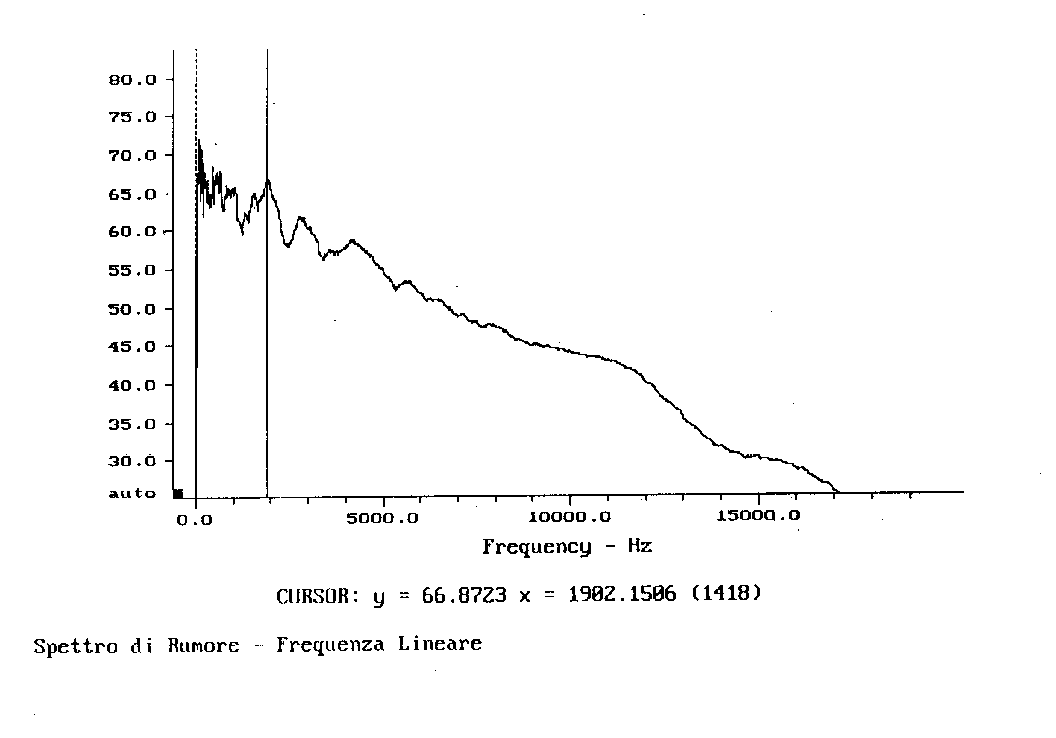
Figura 8
Questo comportamento si può spiegare col fatto che le bande da 1/3 d’ottava sono molto più larghe, ovviamente, di quelle "strette", e quindi possono catturare al loro interno delle zone di frequenze con energia mediamente elevata anche se il picco massimo non è compreso.
Nonostante la precisione degli ultimi due spettri, in ogni caso, il nostro udito rimane meglio rappresentato dal grafico di fig. 6.
Analisi in banda stretta
Un altro metodo per definire lo spettro di un segnale è l’analisi in banda stretta (o di Fourier). Matematicamente è richiesto l’utilizzo della D.F.T. (Discrete Fourier Transformat), che si calcola ormai unicamente per via digitale con l’ausilio del computer.
In questo caso sono però necessarie due ipotesi, non una sola:
Da ciò segue che non è possibile usare l’analisi di Fourier per la voce umana; si può invece per le macchine rotanti, ad es., perché il suono che emettono, anche se complesso, è periodico.
La base matematica che giustifica l’analisi di Fourier è il
Teorema di Fourier
Il teorema di Fourier stabilisce che qualunque suono periodico (anche complesso) è sempre rappresentabile mediante un opportuno numero d’onde (sinusoidi) di determinate ampiezze, frequenze e fasi:
![]() (11)
(11)
Nella pratica però non è possibile usare infinite sinusoidi, anzi, le frequenze che compaiono all’interno della (11) in
![]() (12)
(12)
devono seguire una legge matematica ben precisa; in genere sono equispaziate (fig. 9).
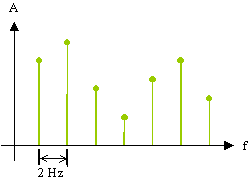
Figura 9
Questa non è più un’analisi di Fourier fatta secondo il teorema, ma è un’analisi discreta in relazione ad una legge matematica inderogabile.
Campionamento
Si definisce campionamento di un segnale continuo il considerare, dello stesso segnale, soltanto determinati valori, presi nel tempo con una frequenza di campionamento fc. In questo modo invece di avere un’onda continua ho N campioni equispaziati di 1/fc.
Ad es., se un segnale con periodo T = 1 s è campionato a fc = 44100 Hz (uno dei valori più comuni), sullo spettro ci saranno 22051 righe: la prima, a 0 Hz, rappresenta la componente continua, l’ultima sarà alla freq. massima di 22050 Hz. Questo valore è detto frequenza di Nyquist ed è definito come la metà della frequenza di campionamento:
![]() (13)
(13)
Ho in pratica una risoluzione di 1Hz. La risoluzione D f è definita come il rapporto tra la frequenza di campionamento e il n° dei campioni
![]() (14)
(14)
ed è uguale alla spaziatura tra le righe dello spettro (fig. 10).
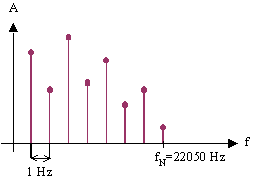
Figura 10
L’analisi di Fourier fornisce, oltre all’informazione d’ampiezza, anche quella di fase, che è necessaria per ricostruire il segnale originario: se non la considerassi avrei una distorsione di fase, e il segnale risulterebbe incomprensibile.
Sistemi a segnale campionato
I sistemi a segnale campionato (computer, DSP, ...) si utilizzano per fare l’analisi in bande di 1/3 d’ottava. Si possono applicare anche a segnali non periodici, e sono anche più simili, come modo di operare, al sistema uditivo umano.
Si parte da un segnale campionato, che conosco quindi ad intervalli di tempo D t .
Bisogna innanzi tutto introdurre una regola fondamentale riguardo al campionamento, il
Teorema di Shannon
Il teorema di Shannon afferma che la frequenza di campionamento di un segnale deve essere
![]() (15)
(15)
dove fMAX è la frequenza massima contenuta nel segnale.
Se la relazione (15) non è rispettata, le componenti del suono a frequenza maggiore vengono sottocampionate e quindi appaiono come elementi a frequenze basse. Campionando una sinusoide che aumenta di frequenza, ad es., superata la frequenza di Nyquist il tono che si sente non sale più di frequenza, al contrario si abbassa. Questo fenomeno è detto aliasing (vedi fig. 11).
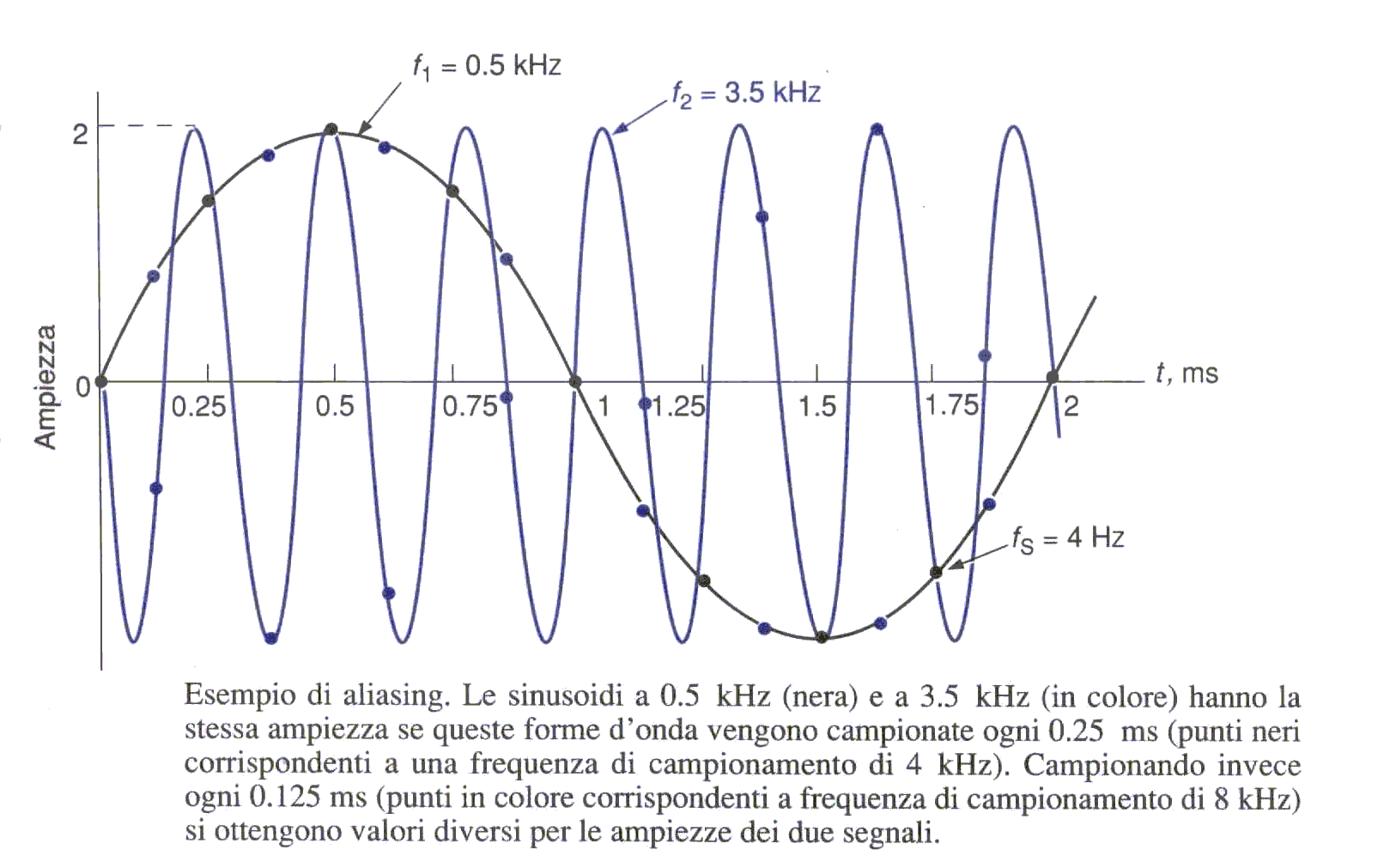
Figura 11
E’ ovvio che campionando un segnale a 44100 Hz ciò non si nota più, perché la frequenza di Nyquist è 22050 Hz che è fuori del campo uditivo. Siccome i microfoni da misura e la strumentazione acustica vengono in genere costruiti con una banda passante fino a 20-22 kHz, la frequenza di campionamento deve essere maggiore o uguale a 44 kHz. Comunque, tanto maggiore è, meglio è, perché avrò più informazioni e commetterò meno errori.
Negli ultimi anni, infatti, si è avuto un continuo aumento delle frequenze di campionamento:
Per applicazioni musicali non è così importante avere una frequenza di campionamento molto elevata; sono fattori critici invece la stabilità e il rapporto segnale – rumore, che dipende dal numero di bit utilizzati per la memorizzazione dei dati. Tradizionalmente i sistemi più "antichi" sono a 16 bit (ad es. i CD o le schede audio di computer più vecchi), si è passati poi a sistemi di fascia media (come i DAT e i DVD) che usano 20 ~ 24 bit di risoluzione. Lo stato dell’arte è attualmente costituito da sistemi a 192 kHz e 24 bit. Andare oltre con la risoluzione non ha molto senso in quanto già con 24 bit si ha un rapporto segnale – rumore molto elevato, di quasi 196 db.
Uno schema d’esempio di sistemi di elaborazione digitale dei segnali è in fig. 12, dove con A/D si è indicato il convertitore analogico – digitale e con D/A il blocco che effettua l’operazione contraria.

Figura 12
Un es. di applicazione in cui la frequenza di campionamento elevata è indispensabile è la teoria dei modelli: in un modello in scala 1:10 le frequenze sono dieci volte quelle nel mondo reale.
Ora la domanda è: come si può emulare la risposta di un filtro passa – banda tramite un apparato digitale?
Serve un filtro numerico, cioè un sistema che opera sui campioni del segnale tramite una formula matematica (fig. 13).

Figura 13
Bisogna in pratica vedere come si ottiene y(i) partendo da x(i). La forma generale del filtraggio digitale dice:
![]() (16)
(16)
La (16) è la struttura di un filtro FIR (Fined Impulse Response, a risposta impulsiva finita); la risposta all’impulso è la successione dei coefficienti A0, A1,... , AN. Questi rappresentano anche la funzione di trasferimento del filtro, anch’essa campionata alla frequenza fc. La risposta all’impulso è definita come la risposta del sistema quando l’ingresso è costituito dalla particolare stringa di numeri detta sequenza di Dirac, o delta di Dirac, che consiste nel valore "1" seguito da tanti "0", e risulta essere la sequenza dei coefficienti A0, A1,... , AN.
Il filtro ha una risposta all’impulso finita (nel tempo) perché se eccitato con una delta di Dirac l’uscita fornisce N campioni non nulli e poi degli zeri.
Questo filtro non è molto potente ma è sicuramente stabile, cioè non oscilla, ed è in grado di applicare qualsiasi filtraggio al segnale. Utilizzando una struttura di tipo FIR è quindi possibile calcolare i coefficienti del filtro in modo che lo stesso emuli la risposta in frequenza di un filtro d’ottava o di 1/3 d’ottava all’interno delle tolleranze prescritte dalle norme IEC.
Un altro metodo operativo si serve del cosiddetto filtro ricorsivo, una struttura più complessa in cui la risposta in un certo istante dipende non solo dall’ingresso in quello stesso istante ma anche dai valori d’uscita precedenti.
Formalmente:
![]() (17)
(17)
In genere M < N. Il filtro è detto "ricorsivo" perché i dati prodotti in uscita sono usati anche come parte dell’ingresso.
In questo caso si ha una risposta all’impulso infinita in quanto, una volta eccitato, elaborando la stessa uscita che fornisce continua ad emettere dei dati; per questo è detto filtro IIR (Infinite Impulse Response, a risposta impulsiva infinita).
L’ampiezza dell’uscita comunque, anche se è sempre ¹ 0, tenderà asintoticamente a tale valore, e quindi ai fini pratici si può comportare come un filtro FIR, purché non sia instabile (ciò può accadere se i coefficienti B sono troppo grandi).
E’ un filtro più efficiente di quello FIR, perché con un numero ridotto di campioni (e quindi di calcoli) fornisce un’uscita migliore. Gli analizzatori di spettro digitali infatti utilizzano filtri IIR che con i coefficienti opportunamente calcolati forniscono uscite stabili e risposte in frequenza all’interno delle tolleranze dettate dalle norme in vigore.
Segnali non stazionari
L’analisi di segnali non stazionari non è in realtà un problema per i sistemi basati su filtri analogici in tempo reale: l’unico accorgimento è quello di "catturare" e memorizzare i dati al volo, e se ciò viene effettuato in maniera sufficientemente rapida si ottiene quello che si chiama un multispettro, cioè una serie di spettri nel tempo. Si ottiene campionando i valori istantanei dello spettro ogni un certo numero di ms.
Esempi di multispettri sono rappresentati nelle fig. 14 e 15, che rappresentano entrambe il sorvolo di un aereo. Si vede che sono possibili diversi tipi di visualizzazione; in ciascuna delle due figure il grafico in 2 dimensioni è detto sonogramma, e riporta il livello in db variando il grado di "nero", mentre il grafico sottostante è una raffigurazione del tipo waterfall (cascata).
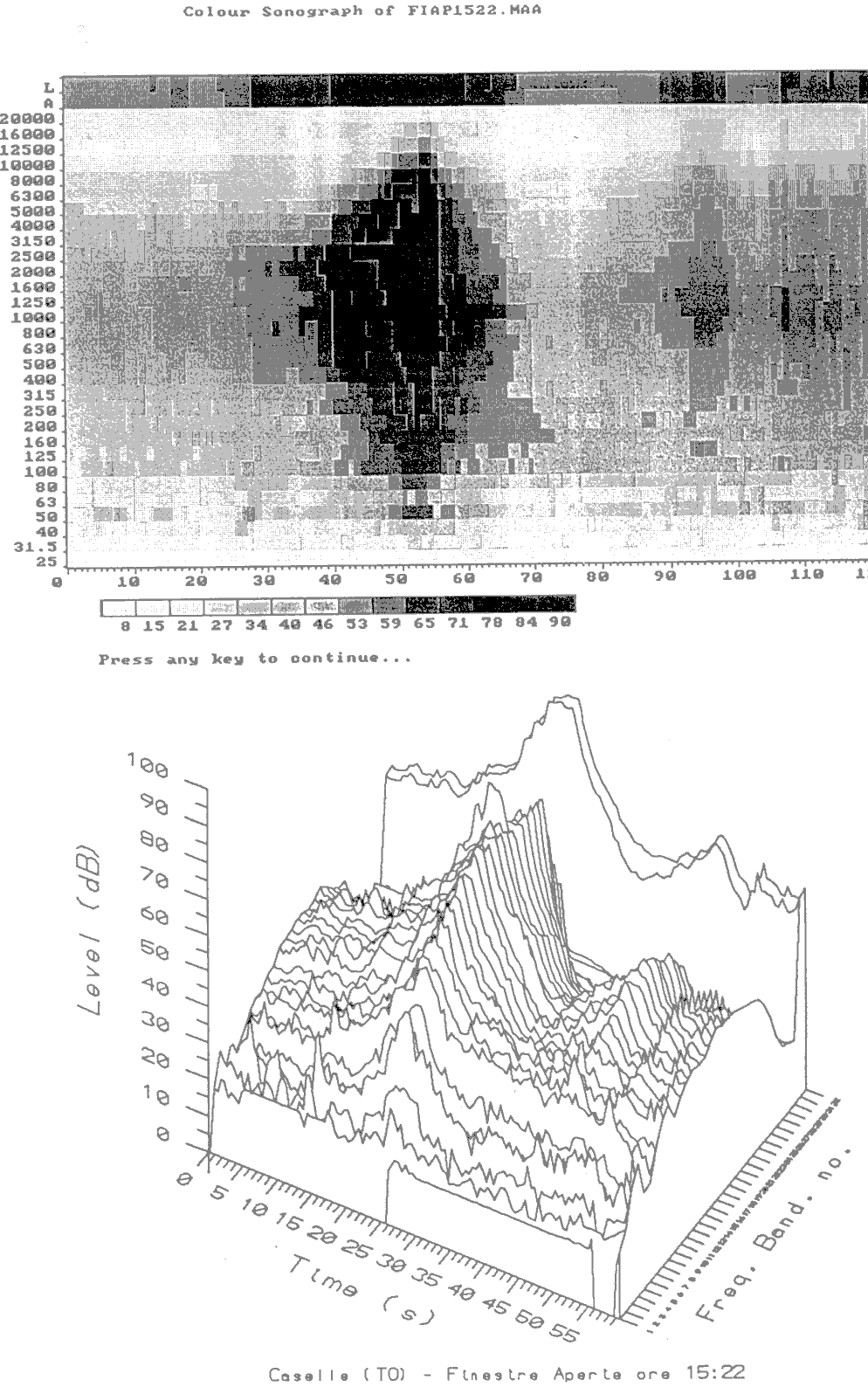
Figura 14
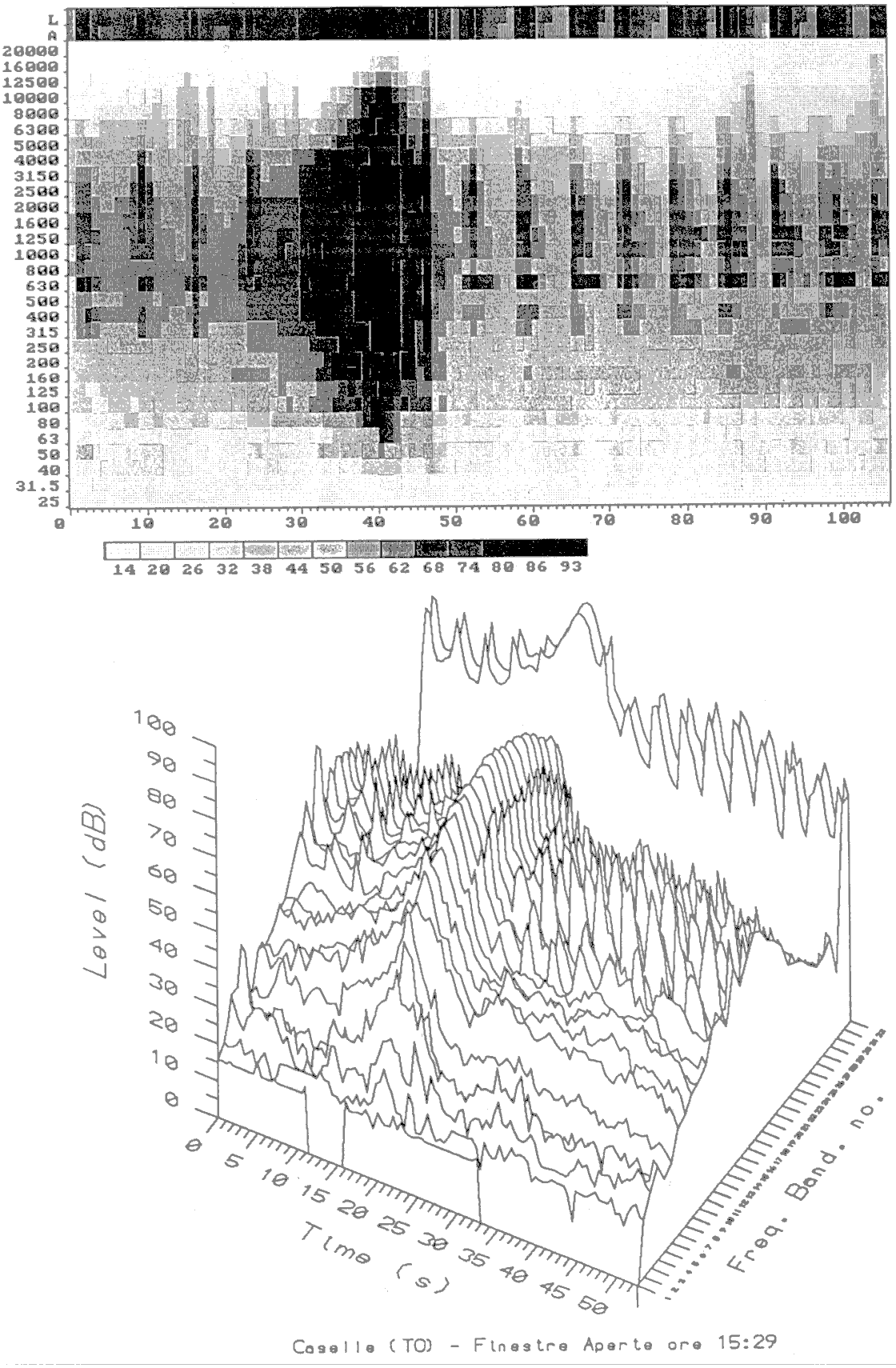
Figura 15
Usando un’analisi in bande percentuali costanti non ci sono quindi grosse difficoltà.
E se si volesse usare un’analisi di Fourier? In teoria non si può fare, ma in pratica questo succede, spesso perché non si ha a disposizione niente di meglio. Ci sono però dei problemi, in quanto il suono non è periodico: al termine della finestra del segnale campionato questo non assume lo stesso valore che aveva all’inizio della finestra, e quindi non è continuo con la finestra successiva. Nel caso di un segnale periodico potrebbe inoltre capitare che la finestra di campionamento non coincida con il periodo del segnale stesso a causa del numero di punti di campionamento, che deve essere una potenza di 2 affinché il calcolo della trasformata discreta di Fourier sia veloce.
Posso allora pensare di creare una "giunzione" matematica tra i due diversi valori ed effettuare poi l’analisi di Fourier, ma così facendo lo spettro che calcolo è diverso da quello vero che mi potrei aspettare o che voglio. Per una sinusoide, ad es., accade come in figura 16, dove lo spettro, invece di avere energia solo alla frequenza dell’onda stessa, si abbassa e si allarga e presenta energia lungo gran parte dell’asse delle frequenze; questo perché ho in sostanza introdotto un gradino nel giuntare due finestre di campionamento successive. Questo fenomeno è detto lickage.
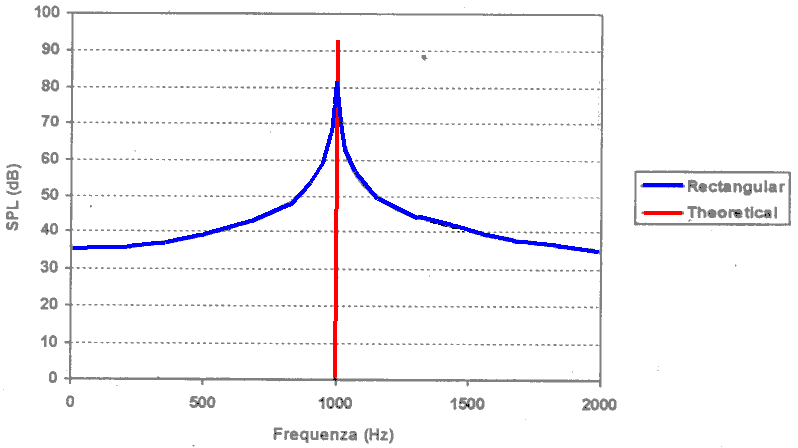
Figura 16
In genere per ovviare a questo problema si forza il segnale ad andare a zero agli estremi della finestra, applicando una sorta di filtro di copertura; in pratica si moltiplicano tutti i punti campionati per una window che annulla il segnale agli estremi. Queste finestre vengono moltiplicate per il segnale in intervalli che si sovrappongono, cioè ad ogni passo si sposta ("shifta") la finestra verso il basso non di N campioni, ma di N/2, in modo che nessuna parte dell’onda venga completamente annullata e per questo tralasciata dall’analisi (fig. 17).
Esistono varie di queste funzioni che servono per modificare il segnale prima di effettuare l’analisi di Fourier. In fig. 18 ne sono riportate alcune nel dominio della frequenza.
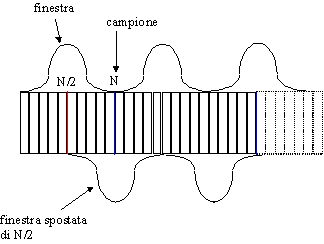
Figura 17
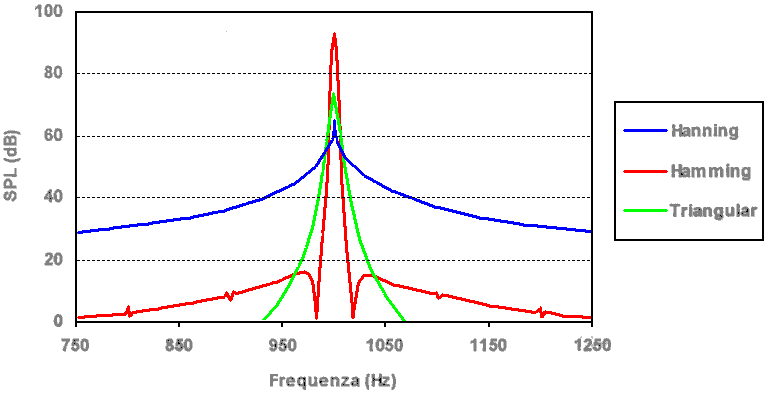
Figura 18