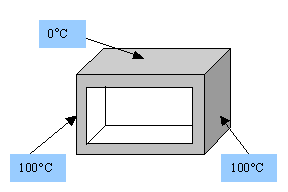
Esercizio 1: Convezione naturale all’interno di un condotto
E’ dato un condotto a sezione rettangolare contenente dell’aria ferma, si vuole determinare il valore della temperatura Ti alla quale si porterà il fluido presente all’interno del condotto:

Figura 1
Le pareti che limitano il condotto si trovano in condizioni differenti:
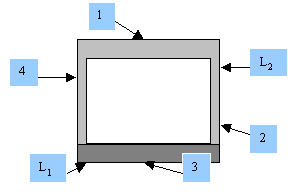
Figura 2
|
L1=2m |
L2=1.5m |
T2=T4=100°C |
T1=0°C |
La superficie inferiore (3) è termicamente isolata, si interpreta come una "faccia" adiabatica, cioè non da luogo ad alcuno scambio di calore.
Descrizione del fenomeno
L’aria al contatto con le pareti laterali si scalda e sale fino al soffitto dove si raffredda e ridiscende. Questo fenomeno si verifica vicino ad entrambe le pareti, perciò si ipotizzano dei percorsi preferenziali per l’aria che si possono individuare nelle vicinanze delle pareti laterali per la salita e centrali per la discesa. Si instaura un moto convettivo naturale che coinvolge tutto il fluido presente all’interno del condotto e che quindi si porterà ad un determinato valore di temperatura Ti, che rappresenta la temperatura media dell’aria. Intuire come avviene il moto del fluido in convezione naturale è molto importante perché fa capire dove avviene il massimo scambio termico e dove, eventualmente, non se ne verifica, come ad esempio nelle vicinanze della parete inferiore.
Soluzione
Per risolvere l’esercizio risulta comodo l’utilizzo di una rete elettrica equivalente che rappresenti i flussi di calore che le tre pareti scambiano con il fluido presente nel condotto. A tale proposito vengono utilizzati tre rami associati ai tre percorsi preferenziali dell’aria a cui corrispondono le resistenze elettriche presenti in figura:
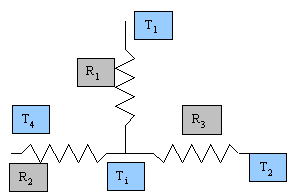
Figura 3
Con i valori delle resistenze termiche che sono:
|
|
|
|
Poiché T2 e T4 sono maggiori di T1 il flusso sarà entrante in direzione del nodo centrale. Il problema risulta indipendente dalla terza dimensione perché il condotto si sviluppa in orizzontale e qualsiasi tratto si troverà ad essere sempre nella medesima situazione, perciò assumiamo un valore che risulti comodo per svolgere i conti pari a 1m. Le resistenze termiche dovute alla convezione sono date dalla seguente espressione:
![]()
Dove h rappresenta il coefficiente di convezione, L la larghezza del condotto e z la sua lunghezza che come detto precedentemente risulta ininfluente ai fini del calcolo della Ti e che perciò è stata assunta pari a 1m.
Il problema dello scambio termico presenta una completa simmetria rispetto al centro del condotto, cioè rispetto al ramo 1 del circuito equivalente, che quindi può essere semplificato:
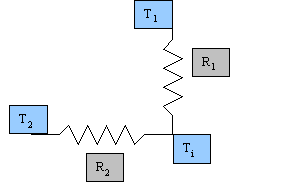
Figura 4
Il parallelismo tra problema termico e circuito elettrico risulta evidente: le correnti nei rami rappresentano i flussi di calore scambiati e i potenziali ai nodi le temperature delle pareti. Con questa semplificazione si è ottenuto un partitore di tensione, da cui è facile ottenere il valore di potenziale del punto intermedio, che rappresenta l’incognita dell’esercizio, cioè proprio la temperatura media dell’aria Ti. Come primo passo si ricava il flusso totale, che è anche uguale allo scambio termico lungo la prima resistenza, perciò:
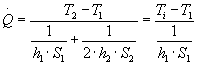
Da cui si ottiene l’espressione della temperatura incognita:
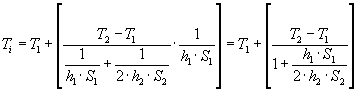
Il vero problema ora è di determinare i coefficienti di convezione h1 e h2, cioè di determinare i numeri di Nusselt, ma essendo questa una convezione naturale all’interno delle espressioni dei numeri di Nusselt si avranno i numeri di Grashof e all’interno delle espressioni di questi ultimi si avrà la temperatura Ti che è l’incognita. Questi problemi, come si è già osservato, si risolvono partendo da un congruo valore di tentativo, quindi per prima cosa è necessario assumere un ragionevole valore di tentativo della temperatura dell’aria presente all’interno del condotto che indicheremo con:
Ti*=60°C
La lunghezza caratteristica L si considera unitaria essendo irrilevante ai fini del problema; il valore di n , cioè della viscosità cinematica dell’aria si ottiene dalle tabelle, cercandone il valore a 60°C:
n =1.89 10-5 m2/s
Il valore del coefficiente di dilatazione termica b in questo caso, essendo l’aria un gas perfetto, è dato da:
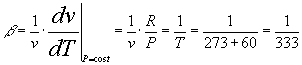
Con il valore di tentativo della temperatura e questi parametri possiamo calcolare il numero di Grashof nel caso della faccia superiore:
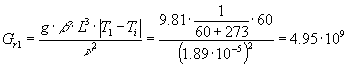
Per l’aria il valore del numero di Prandtl è sempre 0.71, perciò dal numero di Grashof è possibile calcolare subito il numero di Rayleigh:
![]()
Essendo questo valore maggiore di 109 concludo che il moto è turbolento, perciò dalle tabelle che indicano la formula di scambio termico in funzione del regime di moto si ottiene:
C=0.14 b=0.333
Che sostituiti nella formula generale determinano l’espressione per il calcolo del numero di Nusselt:
![]()
Da questa espressione si può ricavare il valore del coefficiente di convezione:
![]()
Dove il valore di l dell’aria è dipendente dalla temperatura e il cui valore si ricava dalle tabelle per la temperatura di 60°C.
Gli stessi calcoli vanno ripetuti per la seconda superficie, quella verticale:
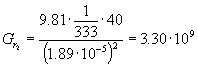
Dato il numero di Grashof si ricava quello di Rayleigh:
![]()
Da cui si deduce che anche su questa parete il moto risulta essere turbolento e dalle tabelle si ottengono i seguenti valori dei coefficienti:
C=0.13 b=0.333
L’espressione del secondo numero di Nusselt risulta perciò:
![]()
Da cui si ricava il secondo coefficiente di convezione:
![]()
Avendo trovato entrambi i valori dei coefficienti di convezione si può calcolare il valore della temperatura media dell’aria:
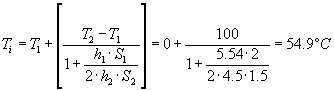
Il valore di tentativo non era esattamente quello corretto, perché un errore di cinque gradi non è enorme, però non è neanche trascurabile, è necessario ripetere i calcoli considerando un nuovo valore di tentativo, che si assume pari a 55°C, per cui:
![]()
Così come b anche i valori di l e n saranno differenti perché dipendenti dalla temperatura, si ottengono i seguenti risultati:
![]()
Da cui:
![]()
Che determina ancora un moto turbolento sulla superficie orizzontale, con il seguente numero di Nusselt:
![]()
Con il seguente coefficiente di convezione:
![]()
Stessi identici ragionamenti per la superficie verticale:
![]()
![]()
![]()
Cioè moto turbolento con:
![]()
Con il valore della temperatura media pari a:
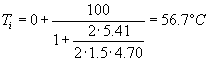
Volendo si può fare un’altra iterazione, ma è inutile cercare una precisione eccessiva, una iterazione è sempre consigliata ma se ci si accorge che il dato non si modifica più di tanto allora si può terminare l’esercizio, perché non si può sapere quanto, numericamente, cambiare i dati in ingresso produce variazioni sull’uscita.
Esercizio 2: Isolamento di una tubazione
E’ dato un tubo d’acciaio all’interno del quale scorre dell’acqua refrigerata con una copertura di isolante, il cui spessore deve essere dimensionato in modo tale che non si formi della condensa sulla superficie del tubo, perché le goccioline di acqua cadrebbero rovinando ciò che si trova sotto, oltre che arrugginire il tubo stesso.
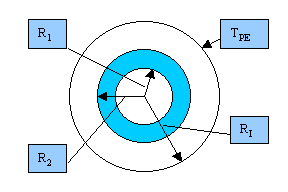
Figura 5
|
R1=13mm |
R2=17mm |
tacqua=5°C |
j ¥ =0.5 |
|
t¥ =20°C |
w=1m/s |
TPE>10°C |
RI= ? |
In questo esercizio non si assume la temperatura del fluido ad una certa distanza dalle pareti, ma la temperatura media del film, cioè la media aritmetica tra la temperatura del fluido lontano dalla parete e la temperatura di parete stessa. A questo valore di temperatura si fanno riferimento tutte le proprietà del fluido, perché è ovvio che la temperatura del fluido che sta scambiando calore non rimane ad un valore fisso, ma varia anche in relazione al punto dove si va a considerare, e quindi anche le proprietà assumono dei valori intermedi tra quelle della temperatura T¥ e T1.
Un dato fondamentale è il grado igrometrico dell’aria che si trova nell’ambiente, perché grazie a quest’ultimo e alla temperatura, è possibile trovare lungo un raffreddamento a titolo costante (perché è questo che accade nelle vicinanze del tubo), la temperatura alla quale si verifica condensa sul tubo:
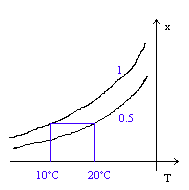
Figura 6
La temperatura alla quale si forma la condensa è detta temperatura di rugiada e vale:
Tr=10°C
Perciò se l’aria si troverà a contatto con una superficie che si trova ad una temperatura maggiore di 10°C allora non si avrà condensa, altrimenti se la superficie esterna del tubo si troverà ad una temperatura inferiore ai 10°C si coprirà di goccioline. Il raggio dell’isolante deve perciò essere tale da fare in modo che la temperatura della parete esterna sia maggiore della temperatura di rugiada, non deve ovviamente essere neanche esagerato perché potrei avere una temperatura superiore a quella minima richiesta, ma con uno spreco di materiale isolante, cioè non c’è nessun bisogno che la temperatura sia molto maggiore di quella di rugiada, è sufficiente che sia appena superiore, in modo da risparmiare anche sui costi di fabbricazione.
Consideriamo sempre il problema in termini di circuito elettrico equivalente, costituito da quattro resistenze termiche, che rappresentano la convezione dentro al tubo, la conduzione nella parete d’acciaio, la conduzione nello strato isolante e la convezione nell’ambiente esterno:
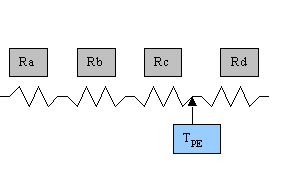
Figura 7
|
|
|
|
|
|
In realtà sappiamo che la resistenza termica nella parete di acciaio è trascurabile, però ai fini dell’esercizio è utile considerarla. Il coefficiente di convezione esterno è indicato come hTOT perché è possibile avere anche la presenza di una quota di irraggiamento. La dimensione longitudinale del tubo è irrilevante ai fini della soluzione perciò possiamo assumere un valore unitario; tale dimensione non coincide con la lunghezza caratteristica che in questo caso è rappresentata dal diametro del tubo.
Cominciamo dunque con il calcolo della convezione interna, per cui serve il numero di Reynolds, e nella cui espressione compare il valore della velocità dell’acqua, che si può assumere pari a 1m/s:
![]()
La viscosità cinematica si ricerca sulle tabelle, osservandone il valore alla temperatura di 5°C. Con questo valore di Reynolds mi accorgo di avere a che fare con un moto turbolento, e quindi di avere i seguenti valori:
C=0.023 a=0.8 c=0.4
Il valore di c è pari a 0.4 poiché questo è il caso in cui l’acqua riceve calore dalla parete esterna.
Il valore del numero di Prandt per l’acqua è anch’esso tabellato in funzione della temperatura e vale, a 5°C, esattamente 12.2, perciò il numero di Nusselt è dato da:
![]()
Da questa espressione si ricava il coefficiente di convezione h:
![]()
Il valore delle quattro resistenze termiche in analogia con il circuito elettrico si sommano e mi determinano una resistenza totale che per definizione è uguale al salto di temperatura complessivo diviso il flusso di calore:
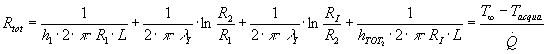
Per poter risolvere questo esercizio è necessario seguire un procedimento che si può definire di ipotesi e verifica, cioè per poter procedere nei calcoli è necessario indicare un valore del raggio dell’isolante che mi determinerà un valore della temperatura della parete esterna del condotto che se sarà maggiore di 10°C andrà bene, altrimenti si dovrà considerare un nuovo valore del raggio dell’isolante e ripetere i calcoli. La differenza con il procedimento dell’esercizio precedente consiste nel fatto che la variabile oggetto dei tentativi è una variabile discreta e non continua, perché non esistono valori qualsiasi dei diametri dei tubi di isolante, ma esistono solo determinati valori commerciali tra i quali si può scegliere il valore di:
RI*=20mm
Con questo valore andiamo a calcolare il valore del coefficiente di convezione esterno, ricordandoci che ci troviamo in convezione naturale. Come primo passo si deve ricavare il numero di Grashof, ricordandosi che nel caso di gas perfetti si ha che il coefficiente di dilatazione termica è dato dall’inverso della temperatura, che in questo caso indichiamo con la temperatura media del film, cioè tra 10°C e 20 °C, pari a 15°C:
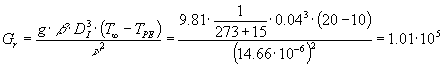
Dove Di è il diametro dell’isolante.
Il numero di Rayleigh perciò, ricordandosi che nel caso dell’aria il numero di Prandtl vale sempre 0.71, è dato da:
Ra=Gr*Pr=1.01 105 0.71=72000
Con questo caso geometrico e questo valore di Rayleigh si ottengono le seguenti costanti:
C=0.53 b=0.25 c=0.25
Che determinano, per l’esterno, il seguente numero di Nusselt:
![]()
Da cui si ricava il coefficiente di convezione:
![]()
L’unica parte che manca è quella radiante dove lo scambio termico per irraggiamento per unità di superficie (q) è dato dal coefficiente di assorbimento (a) per la costante di Boltzman (s 0) per la differenza tra la temperatura di parete esterna e quella all’infinito. Il valore di a dipende da quanto il nostro materiale è nero, cioè se fosse perfettamente nero varrebbe uno, e nel nostro caso vale 0.9. La costante di Boltzman invece vale:
![]()
Perciò:
q = a s 0 ï TPE4-T¥ 4ï
Come si può osservare in questa equazione c’è una dipendenza dalla temperatura non lineare, mentre nel circuito si ha la presenza di carichi lineari, perciò occorre linearizzare l’equazione forzando l’uguaglianza a un opportuno coefficiente di irraggiamento che moltiplica la differenza tra le temperature:
q = a s 0 ï TPE4-T¥ 4ï = hirï TPE-T¥ ï
Da cui si ottiene la parte del coefficiente di convezione esterno dovuto all’irraggiamento:
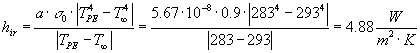
Si è in grado, a questo punto, di determinare il coefficiente di convezione esterno sommando il contributo di irraggiamento a quello di convezione:
![]()
La potenza termica scambiata risulta:
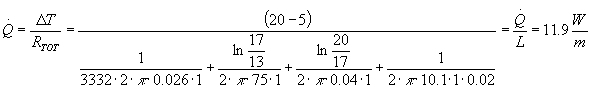
Scrivendo la legge di Ohm sull’ultima resistenza si ottiene la temperatura di parete esterna desiderata:
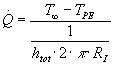
Da cui:
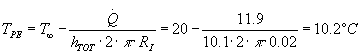
Il fatto che il risultato sia corretto al primo tentativo è fortuito, se così non era, sarebbe stato necessario cambiare il diametro dell’isolante e ripetere i calcoli.
Esercizio 3: Scarico in mare del liquame da un impianto di purificazione
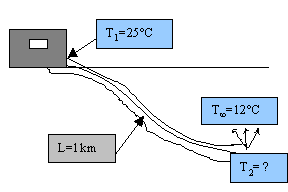
Figura 8
All’interno dell’impianto di trattamento avvengono processi di fermentazione del liquame stesso, processi di tipo esotermico, cioè producono calore. Dopo che la fermentazione ha avuto successo, cioè dopo che la carica organica è stata degradata dall’azione dei batteri, il liquame lascia l’impianto ad una temperatura molto elevata attraverso una conduttura che lo porta ad una determinata distanza dalla costa. Raggiunta questa distanza il liquame viene gettato in acqua, che di solito si trova ad una temperatura molto inferiore, circa di 12°C, e di conseguenza il liquame, più caldo, viene a galla, producendo uno sgradevole fenomeno di galleggiamento. Realizzare un tubo lungo ha quindi una duplice funzione: da una parte di allontanare il problema dalla riva (nel caso di fenomeni di galleggiamento), e dall’altra di produrre un maggiore scambio di calore con l’esterno in modo da arrivare alla fine del tubo, quando il liquame si getta nell’acqua marina, con una minore differenza di temperatura, in modo tale che si adagi sul fondale o si mescoli con l’acqua, senza cioè il fenomeno della risalita.
Consideriamo una struttura con le seguenti caratteristiche:
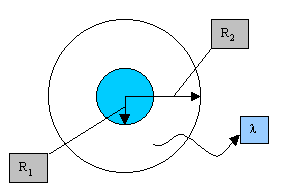
Figura 9
|
R1=150mm |
R2=180mm |
W=2m/s (portata del tubo) |
|
Le proprietà termodinamiche del liquame sono sensibilmente simili a quelle dell’acqua, perciò si assumono uguali. L’acqua fuori dal tubo si considera ferma, perciò si ipotizza una situazione di convezione naturale, che è l’ipotesi peggiore, perché quando c’è corrente o mare mosso il maggiore scambio termico migliora la situazione. Nota la temperatura T¥ del mare e quella T1 con cui il liquame entra nel condotto, vogliamo determinare la temperatura T2 con cui il liquame esce dal condotto.
Utilizzando il solito parallelismo con le resistenze termiche otteniamo:
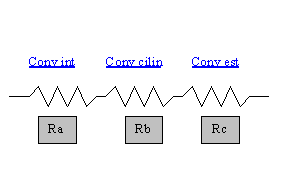
Figura 10
|
|
|
|
In figura sono rappresentate, procedendo da sinistra verso destra, la convezione interna, la conduzione nello strato cilindrico e la convezione esterna.
La potenza termica scambiata si può ottenere passando attraverso la resistenza termica totale:
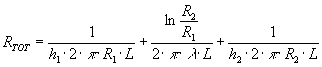
Da cui:
![]()
Da queste formule è possibile ricavare il valore dei coefficienti di convezione. Il primo problema che si incontra è però quello di determinare il valore della differenza di temperatura, che non è costante, perché all’inizio vale 25-12, ma alla fine è più bassa, è T2-12, infatti diagrammando la temperatura in funzione dell’ascissa x si ottiene:
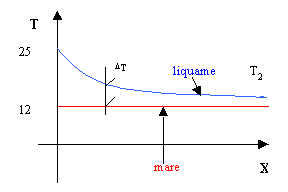
Figura 11
Assumere come D T il suo valore iniziale è quindi clamorosamente sbagliato, perché porterebbe ad una sovrastima dello scambio termico e quindi ad una pericolosa sottostima del valore della temperatura in uscita. Una prima soluzione del problema potrebbe essere quella di ipotizzare un decadimento lineare del valore del D T e quindi l’assunzione di un D T medio pari a:
![]()
Che ovviamente non è ancora corretto. La soluzione corretta consiste nel valutare il D T medio logaritmico:
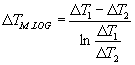
A questo punto l’incognita compare esplicitamente all’interno dell’espressione:
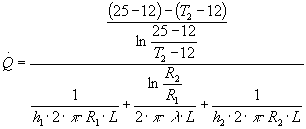
Questo non è però un problema come quelli precedenti, non si ha da assegnare un valore di tentativo, si hanno due incognite, è necessaria un’altra equazione, che si ricava dal primo principio della termodinamica. La quantità di calore scambiata può essere scritta in due modi: con le formule dello scambio termico, oppure con il primo principio della termodinamica:
![]()
Dove la portata in massa è data da:
![]()
Con A che rappresenta l’area di passaggio del tubo:
A = p R12
Da cui si ottiene:
![]()
Uguagliando le due formule della potenza termica si ottiene come unica incognita proprio la temperatura desiderata.
Esercizio 4: Tiraggio di un camino
Consideriamo un camino con le seguenti caratteristiche:
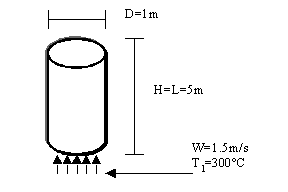
Figura 12
Si hanno dei fumi caldi che risalgono il camino per il fatto che sono caratterizzati da una densità minore di quella dell’aria circostante in virtù del fatto che sono caldi, ed è già stato calcolato in precedenza che la portata può essere ad esempio di 1.5m/s. La temperatura di ingresso dei fumi si considera pari a 300°C. Il camino è costituito da un sottile foglio di lamiera di spessore e resistenza termica trascurabili, perciò i fumi risalendo disperdono inevitabilmente calore con l’ambiente esterno che si trova ad una temperatura di 10°C. La domanda che ci si pone è a quale temperatura questi fumi usciranno dal camino. Anche in questo caso siamo di fronte ad un problema di natura ambientale, perché anche ora, come nell’esercizio precedente, si può avere un fenomeno di risalita dei fumi, oppure un effetto stagnante o addirittura di discesa. A differenza del caso precedente si vuole che i fumi in uscita dal camino salgano il più possibile, perciò si vuole che questi fumi escano più caldi possibile, perché se fossero troppo freddi si potrebbe verificare un fastidioso fenomeno di ricaduta di polverino nero poco igienico e salutare, mentre se salissero molto in alto la concentrazione si ridistribuirebbe su grosse quantità d’aria e quella presente al suolo risulterebbe talmente bassa da non danneggiare nessuno.
Questo problema si imposta formalmente come nel caso precedente, con la stessa espressione per il D T medio logaritmico, perciò la potenza scambiata avrà la seguente espressione:
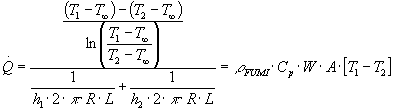
L’espressione risulta un poco più semplice di quella precedente perché ora è stata trascurata la resistenza termica della parete; A rappresenta l’area del camino.
La differenza si verifica nel calcolo dei coefficienti di convezione: il coeff. di convezione esterna è un coeff. di convezione naturale perché non si ha niente che sta soffiando contro il camino, ma l’ipotesi peggiore in questo caso è la presenza di vento, perché aumenterebbe il coefficiente di scambio termico. E’ perciò cautelativo svolgere i calcoli nel caso di convezione forzata. Resta ancora però poco chiaro come calcolare il coefficiente di convezione dentro il camino, cioè che tipo di convezione si assume all’interno?
Non c’è alcun ventilatore o pompa che fa salire il fumo nel camino, perciò sembrerebbe una convezione naturale, ma in realtà il moto non è causato dallo scambio termico, ma è ostacolato dallo scambio termico: il fumo scambiando calore con la parete fredda aumenta la propria densità, quindi riduce il suo "galleggiamento", e lo scambio termico naturale che si avrebbe farebbe andare in giù il fumo, non verso l’alto. In conclusione c’è una componente naturale dello scambio termico che ha direzione opposta alla componente di moto verso l’alto che è di natura forzata, pur essendo naturale nel senso fluidodinamico del termine.
Se il tiraggio fosse compromesso allora si potrebbe verificare un fenomeno di risalita al centro, ma di discesa vicino alla parete, e in questa condizione ci si troverebbe con uno scambio termico in convezione naturale. Ma se in nessun punto il moto dei fumi si inverte lo scambio termico convettivo deve essere considerato di natura forzata, e quindi calcolato con l’espressione di Dittus-Boelter.
Anche in questo caso servono due equazioni: quella del bilancio dell’energia e quella di scambio termico sul condotto.