Esercizio 1: la caldaia
Una caldaia produce vapore alla pressione di 40 bar e alla temperatura di 300 oC. Supponendo che il sistema parta da una temperatura iniziale di 60 oC, calcolare la quantità di calore necessaria per vaporizzare una massa M pari ad 1 kg di acqua.
Fig.1-schematizzazione di una caldaia
La caldaia è una macchina che funziona prendendo in ingresso dell’acqua allo stato liquido e producendo in uscita del vapore surriscaldato.
In base ai dati che vengono forniti e sapendo che il processo compiuto dalla caldaia è a pressione costante, si ha che le condizioni iniziali e finali sono rispettivamente:
T1 = 60 oC, P1 = 40 bar e T4 = 300 oC, P4 = 40 bar.
Disegnamo sul piano pv la trasformazione operata dalla caldaia.

Fig.2
Indichiamo con q la quantità di calore da determinare: dato che M = 1kg è una quantità di calore per unità di massa.
Applichiamo al sistema il I principio della termodinamica in forma entalpica.
![]() (1)
(1)
Poichè la trasformazione avviene a pressione costante si ha che vdp = 0 e quindi, integrando, il valore richiesto risulta essere uguale al salto di entalpia.
![]() (2)
(2)
Il salto di entalpia può essere espresso come la somma di tre contributi
![]() (3)
(3)
![]() (4)
(4)
Il calore specifico è una grandezza tabulata: nel nostro caso cL = 4,187(kJ/kgK).
![]() (5)
(5)
Nel caso in esame r =1713(kJ/kg).
|
p (bar) |
t (oC) |
hL(kJ/kg) |
r (kJ/kg) |
hv(kJ/kg) |
|
34 |
240,88 |
1041,3 |
1760,3 |
2802,1 |
|
36 |
244,16 |
1057,5 |
1744,2 |
2801,7 |
|
38 |
247,31 |
1072,7 |
1728,4 |
2801,1 |
|
40 |
250,33 |
1087,4 |
1712,9 |
2800,3 |
|
42 |
253,24 |
1101,5 |
1697,8 |
2799,4 |
|
44 |
256,05 |
1115,4 |
1682,9 |
2798,3 |
|
46 |
258,75 |
1128,8 |
1668,3 |
2797,0 |
|
48 |
261,37 |
1141,8 |
1653,9 |
2795,7 |
![]()
![]() (6)
(6)
Sulle tabelle si trova che tra le temperature di 250 oC e 300 oC cpv vale circa 3,1(kJ/kgK).
Tabella del calore specifico medio del vapore d’acqua surriscaldato misurato dalla temperatura di saturazione alla temperatura assegnata
|
P=40atm |
|
|
t (oC) |
cpv(kJ/kgK) |
|
240 |
- |
|
260 |
3,483 |
|
280 |
3,262 |
|
300 |
3,136 |
|
320 |
3,027 |
|
340 |
2,931 |
|
360 |
2,851 |
In generale nel campo dei valori surriscaldati la variazione di entalpia non dipende solo dalla temperatura ma anche dalla pressione: quello in esame è un caso particolare in quanto avviene una trasformazione a pressione costante.
Sostituendo (4),(5) e (6) in (3) si ottiene la quantità di calore cercata
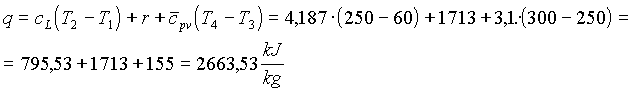
Osservazione: Nel campo del vapore d’acqua, relativamente alle trasformazioni dello stesso tipo di quella operata dalla caldaia, si verifica sempre una sorta di fenomeno di "compensazione". Supponendo di aumentare la pressione e la temperatura si ha che diminuisce il calore latente di vaporizzazione, ma crescono in proporzione i termini di calore relativi alle trasformazioni nel campo del liquido e del vapore surriscaldato. Quindi la quantità di calore necessaria a vaporizzare una massa
di 1kg di acqua è sempre dell’ordine dei 2500-2700(kJ/kg).
Esercizio 2: la pentola a pressione
Si consideri una pentola a pressione, ovvero un recipiente rigido indeformabile dotato di una valvola. La si riempia in parte di acqua e la si metta sul fuoco con la valvola aperta. Fornendo calore al sistema la temperatura dell’acqua cresce fino a raggiungere quella di ebollizione. Supponendo di essere alla pressione P1 = 1 bar, la temperatura di ebollizione risulta essere T1 = 100 oC. Se si continua a fornire calore comincia a prodursi del vapore: questo spinge fuori, attraverso la valvola, l’aria presente nella pentola . Quando tutta l’aria è stata espulsa, la valvola viene chiusa. In questa condizione la pentola contiene del vapore saturo ovvero acqua liquida in equilibrio con il suo vapore. Si supponga che vi siano 10kg di acqua liquida e 1kg di vapore. Determinare l’ulteriore quantità di calore che è necessario fornire la sistema per portare la sua pressione dal valore iniziale P1 al valore P2 = 5 bar e il titolo x2 della nuova situazione di equilibrio.
Fig.1-schematizzazione della pentola a pressione
La trasformazione effettuata dalla pentola consiste in un aumento di pressione a volume costante: il volume non può aumentare in quanto si è supposto il recipiente rigido e indeformabile.
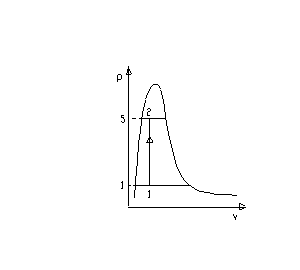
Fig.2- rappresentazione della trasformazione sul diagramma pv
Indichiamo con Q il calore cercato. Applichiamo al sistema chiuso "pentola" il I principio della termodinamica.
![]() (1)
(1)
Dato che la trasformazione non comporta un cambiamento di volume non vi è nessuno scambio di lavoro con l’esterno quindi L=0 e il calore Q risulta essere uguale alla variazione di energia interna
![]() (2)
(2)
Per calcolare le energie interne specifiche del vapore saturo alle pressioni P1 e P2 prendiamo come riferimento gli stati liquidi corrispondenti.
![]() (3)
(3)
![]() (4)
(4)
con ud1 e ud2 energie specifiche differenziali.
Il titolo x1 lo si può calcolare facilmente
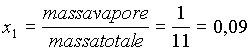 (5)
(5)
Per calcolare il titolo x2 è sufficiente considerare che la trasformazione tra il punto 1 e il punto 2 avviene a volume costante quindi
![]() (6)
(6)
ovvero
![]() (7)
(7)
in cui sono stati usati i volumi specifici degli stati liquidi e i volumi specifici differenziali.
Risolvendo rispetto a x2 si ha
![]() (8)
(8)
![]() (9)
(9)
Possiamo ora sostituire i valori trovati nelle (3) e (4)
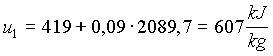 (10)
(10)
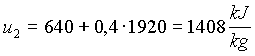 (11)
(11)
sostituendo (10) e (11) in (2)
![]()
I valori numerici sono stati ricavati facendo riferimento alla sequente tabella del vapore d’acqua.
|
p (bar) |
t (oC) |
vL (dm3/kg) |
vG (dm3/kg) |
hL(kJ/kg) |
r (kJ/kg) |
hv(kJ/kg) |
|
0,87686 |
96 |
1,0406 |
1915,3 |
402,2 |
2267,5 |
2669,7 |
|
0,94301 |
98 |
1,0421 |
1789,3 |
410,6 |
2262,2 |
2672,9 |
|
1,01325 |
100 |
1,0437 |
1673,0 |
419,1 |
2256,9 |
2676,0 |
|
1,0878 |
102 |
1,0453 |
1565,5 |
427,5 |
2251,6 |
2679,1 |
|
1,1668 |
104 |
1,0469 |
1466,2 |
435,9 |
2246,3 |
2682,2 |
|
1,2504 |
106 |
1,0485 |
1374,3 |
444,4 |
2240,9 |
2685,3 |
|
1,3390 |
108 |
1,0502 |
1288,9 |
452,9 |
2235,4 |
2688,3 |
|
|
|
|
|
|
|
|
|
p (bar) |
t (oC) |
vL (dm3/kg) |
vG (dm3/kg) |
hL(kJ/kg) |
r (kJ/kg) |
hv(kJ/kg) |
|
4,5101 |
148 |
1,0886 |
412,88 |
623,5 |
2119,5 |
2743,0 |
|
4,7600 |
150 |
1,0908 |
392,45 |
632,1 |
2113,2 |
2745,4 |
|
5,0208 |
152 |
1,0930 |
373,22 |
640,8 |
2106.9 |
2747,7 |
|
5,2929 |
154 |
1,0953 |
355,10 |
649,4 |
2100,6 |
2750,0 |
|
5,5767 |
156 |
1,0976 |
338,03 |
658,1 |
2094,2 |
2752,3 |
|
5,8725 |
158 |
1,0999 |
321,94 |
666,8 |
2087,7 |
2754,5 |
|
6,1806 |
160 |
1,1022 |
306,76 |
675,5 |
2081,3 |
2756,7 |
Esercizio 3: misura del titolo
Si consideri un tubo dentro al quale sta scorrendo del vapore saturo. Tramite un manometro si calcola che la pressione dentro al tubo è P = 40 bar.

Fig.1
Determinare il titolo x1 del vapore.
E’ possibile determinare sperimentalmente il titolo di un vapore saturo che scorre entro un condotto operando secondo lo schema seguente. Sulla parete laterale del condotto viene praticato un foro, di opportune dimensioni, al quale viene collegata una conduttura comunicante con l’esterno. Lungo questa conduttura viene inserita una valvola con l’apertura regolabile a piacere. A valle della valvola è predisposto un punto di misura per la temperatura del vapore fuoriuscente: allo scopo è sufficiente usare un termometro a mercurio. La temperatura letta nel caso in esame è T2 = 115 oC .
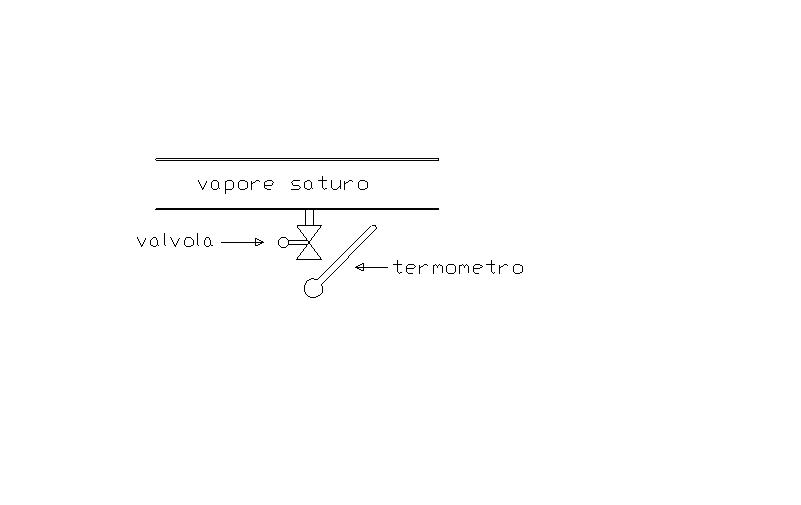
Fig.2
Il condotto entro cui scorre il vapore e la valvola costituiscono un sistema aperto: per determinare il titolo è sufficiente studiare questo sistema supponendo che la fuoriuscita del vapore attraverso la valvola avvenga sotto opportune condizioni.
Nell’ipotesi di poter trascurare i contributi di energia cinetica ed energia potenziale l’equazione di bilancio dell’energia per un sistema aperto può essere scritta come
![]() (1)
(1)
Supponiamo ora che il vapore venga fatto fuoriuscire dalla valvola tramite un processo di laminazione. Supponiamo cioè che l’apertura della valvola sia tale (in generale molto piccola) per cui il vapore esca senza scambiare calore con l’esterno, sia già in equilibrio di pressione con l’ambiente ovvero sia alla pressione atmosferica, e abbia una velocità talmente bassa da poter trascurare qualsiasi termine di energia cinetica. Questa è una trasformazione adiabatica a lavoro nullo: non vi è nessuno scambio di lavoro perché il fatto che il vapore esca in equilibrio di pressione con l’ambiente fa si che non vi sia nessuna espansione . La (1) diventa quindi
![]() (2)
(2)
Rappresentiamo la trasformazione sul diagramma pv. Il percorso tra 1 e 2 è stato tratteggiato in quanto la trasformazione è irreversibile e gli unici stati di equilibrio, e quindi effettivamente rappresentabili, sono quello iniziale e quello finale.
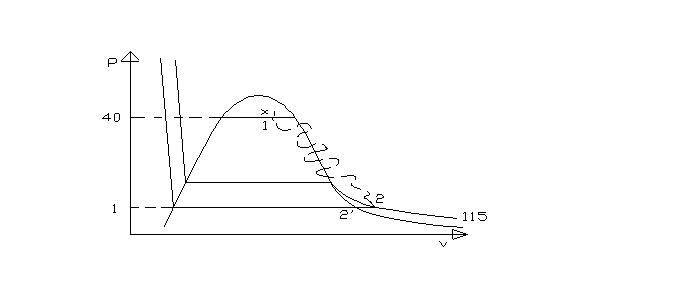
Fig.3
Considerando i valori specifici delle entalpie si ha
![]() (3)
(3)
dove r1 è il calore latente di vaporizzazione alla pressione di 40 bar e hL1 è l’entalpia specifica dello stato liquido corrispondente.
E
![]() (4)
(4)
dove h2 è l’entalpia specifica del vapore surriscaldato, cpv è il calore specifico medio a pressione costante del vapore e 2’ è il punto che si trova sulla curva limite superiore in corrispondenza di una pressione di 1 bar quindi T2’ = 100 oC.
Uguagliando (3) e (4), risolvendo rispetto ad x1 e sostituendo i valori numerici che si possono ricavare dalle tabelle degli esercizi precedenti si ottiene il risultato voluto
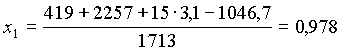 (5)
(5)
I sistemi aperti
Fino ad ora abbiamo affrontato lo studio delle leggi della termodinamica limitandoci a considerare i sistemi chiusi.
Ricordiamo che si definisce sistema chiuso una determinata regione di spazio delimitata da una superficie, reale o apparente, rigida o deformabile, che ne costituisce il confine e ha la proprietà di essere chiusa, ovvero di impedire qualsiasi scambio di materia con l’esterno. La massa di un sistema chiuso è quindi costante e invariante nel tempo: se potessimo marcare le molecole presenti nel sistema ad un dato istante, queste rimarrebbero sempre le stesse anche dopo un tempo t arbitrario e indipendentemente dalle trasformazioni subite dal sistema stesso.
Vogliamo ora estendere il nostro studio al caso dei sistemi aperti e ricavare per essi le equazioni di bilancio della massa e dell’energia. La maggior parte dei problemi termotecnici richiede infatti l’applicazione dei principi della termodinamica a sistemi che scambiano in continuazione materia con l’esterno: tutte le apparecchiature che sono interessate da un flusso di materia rientrano nella categoria dei sistemi aperti.
Vediamo una definizione piu’ rigorosa: un sistema aperto è un determinato volume dello spazio racchiuso da una superficie, detta confine del sistema, attraverso la quale puo’ entrare o uscire una certa quantità di materia. Il confine e il volume in esso racchiuso sono entrambi invarianti nel tempo. Si considerano trasformazioni del sistema aperto tutti i fenomeni che avvengono in questo volume anche se questi comportano un flusso di massa attraverso di esso. Generalmente si definisce il volume che costituisce un sistema aperto facendo riferimento a superficie di confine fisiche: in tal modo la materia non può indistintamente entrare o uscire da ogni punto di esse. La maggior parte della superficie di confine è impermeabile al flusso di materia; presenta poi zone, chiamate sezioni di ingresso, attraverso le quali la massa può entrare nel sistema e zone, chiamate sezioni di uscita, attraverso le quali la massa può uscire.
Il modello più semplice di sistema aperto, che prenderemo come riferimento per la nostra trattazione, è una sorta di tubo con superficie laterali impermeabili, una sola sezione di ingresso e una sola sezione di uscita.
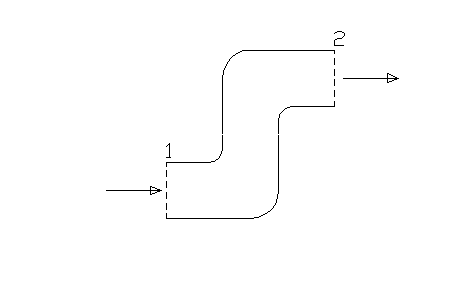
Fig.1
Indichiamo con 1 la sezione di ingresso e con 2 la sezione di uscita.
Sara’ possibile poi estendere le relazioni che troveremo anche al caso di sistemi aperti con più sezioni di ingresso e più sezioni di uscita.
Equazione di bilancio della massa
E’ possibile utilizzare i metodi di indagine termodinamica, già elaborati per il sistema chiuso, anche per l’analisi del sistema aperto. Per fare ciò è sufficiente considerare un sistema chiuso, che chiameremo ausiliario, che si sposta nello spazio per un certo intervallo di tempo, e contemporaneamente una regione, fissa nello spazio, che nel tempo viene attraversata dallo stesso sistema chiuso: questa regione costituisce appunto il sistema aperto.
Le variabili che servono per descrivere un sistema aperto sono esprimibili in funzione della posizione e del tempo.
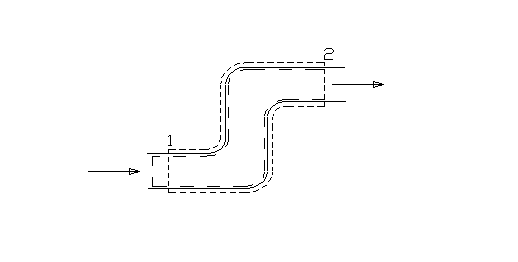
Fig.2
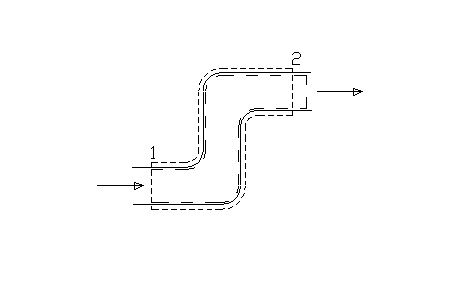
Fig.3
Prendiamo un istante di riferimento t = t0 al quale cominciamo ad osservare i sistemi. Nella situazione iniziale il sistema chiuso ausiliario è definito in modo tale da comprendere tutta la massa contenuta nel sistema aperto più una porzione infinitesima di massa, che chiameremo dM1, collocata immediatamente a monte della sezione 1 di ingresso e che è quindi "pronta" ad entrare nel sistema aperto (fig 2). Lasciamo trascorrere un intervallo di tempo infinitesimo dt sufficientemente lungo per consentire a tutta la massa dM1 di entrare nel sistema aperto. Contemporaneamente si avrà l’uscita dal sistema aperto di una massa infinitesima dM2, in generale diversa da dM1. La massa dM2 è la massa che al tempo t0 si trovava immediatamente a monte della sezione 2 di uscita ed era "pronta" ad uscire dal sistema aperto. All’istante finale di osservazione t = t0 + dt entrambi i sistemi si trovano in uno stato diverso da quello iniziale. Per quanto riguarda il sistema aperto abbiamo che una massa dM1 è entrata e una massa dM2 è uscita. Il sistema chiuso ausiliario invece risulta costituito da tutta la massa contenuta nel sistema aperto più la massa infinitesima dM2 (fig.3).
Dalla definizione di sistema chiuso segue che la massa del sistema ausiliario deve rimanere costante nel tempo. Quindi, poiché il sistema che abbiamo osservato per un intervallo di tempo dt è un sistema chiso, la massa in esso contenuta, pur avendo subito uno spostamento nello spazio, non deve essere cambiata.
Possiamo quindi scrivere un bilancio della massa di questo tipo
![]() (1)
(1)
dove il pedice sc sta per sistema chiuso.
Ma
 (2)
(2)
dove v è il volume contenuto nel confine del sistema aperto e r è il valore locale della densità che può variare da punto a punto del sistema.
E
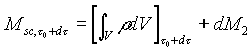 (3)
(3)
Sostituendo (2) e (3) in (1) otteniamo
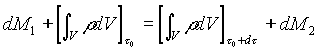 (4)
(4)
Dividendo entrambi i membri di (4) per dt e ordinando si ha
 (5)
(5)
dM1/dt rappresenta la quantità di massa che entra nel sistema aperto nell’unità di tempo, mentre dM2/dt rappresenta la quantità di massa che esce nell’unità di tempo. Esse vengono chiamate portate in massa e si indicano rispettivamente con ![]() e
e ![]() .
.
Ricordando poi che la derivata di un integrale è uguale all’integrale della derivata possiamo riscrivere la (5) come
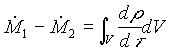 (6)
(6)
Vediamo il significato fisico dell’equazione che abbiamo scritto: poiché la massa non si crea né si distrugge, se entra più massa di quanta ne esce, la densità dentro al sistema aperto deve crescere; mentre se esce più massa di quanta ne entra la densità deve calare.
Sistemi aperti che si comportano in questo modo si dicono in regime non stazionario o transitorio.
Un sistema aperto si definisce invece in regime stazionario se le sue proprietà termodinamiche e meccaniche assumono in ogni punto valori costanti nel tempo. Ciò vuol dire che le particelle che occupano, successivamente nel tempo, un elemento di volume fisso rispetto ad un sistema di riferimento opportunamente scelto si trovano nel medesimo stato fisico ed hanno la medesima velocità.
Se un sistema aperto è in regime stazionario la sua densità rimane costante in ogni punto e quindi (dr/dt) = 0. Ciò fa si che il secondo membro della (6) si annulli: si ottiene che la portata in massa che entra è uguale alla portata in massa che esce
![]() (7)
(7)
Nella nostra trattazione considereremo sempre, per semplicità, sistemi in regime stazionario. I regimi transitori verranno approsssimati con una successione di stati stazionari.
Equazione di bilancio dell’energia
E’ possibile calcolare l’entità degli scambi energetici tra sistema aperto e ambiente esterno seguendo la stessa logica usata per ricavare l’equazione di bilancio della massa: anche in questo caso faremo riferimento ad un sistema chiuso ausiliario.
Per scrivere l’equazione che esprime il principio di conservazione dell’energia per un sistema aperto dovremo prendere in considerazione anche forme di energia che avevamo supposto trascurabili nella trattazione dei sistemi chiusi (energia cinetica ed energia potenziale) in quanto avevamo considerato sistemi privi di un moto di insieme.
All’istante di riferimento t = t0 il contenuto energetico del sistema chiuso ausiliario è dato dalla somma dell’energia dE1 che compete alla massa dM1 e di quella che compete alla massa racchiusa entro il volume v del sistema aperto.
dE1 può essere espressa come la somma di tre contributi: energia interna, energia potenziale gravitazionale ed energia cinetica.
L’energia interna può essere espressa come il prodotto della massa infinitesima dM1 per l’energia interna specifica u1
![]() (8)
(8)
L’energia potenziale per unità di massa è uguale al prodotto dell’accelerazione di gravità g per la quota z a cui si trova la massa dM1 nel campo gravitazionale, avendo preso come quota di riferimento il livello del mare.
![]() (9)
(9)
Per il calcolo dell’energia cinetica è necessario tenere presente la sua dipendenza dalla velocità del fluido.
La velocità di un fluido che si muove all’interno di un condotto non è costante in ogni punto, ma, al variare del tipo di moto da cui è interessato il fluido, varia in funzione della sezione che si prende in considerazione e della distanza dall’asse del condotto ( supponiamo di avere condotti di forma geometrica regolare o comunque dotati di simmetria).
I tipi di moto di un fluido all’interno di un condotto sono infiniti e variano tra le condizioni estreme di moto laminare (fig.4) e moto turbolento (fig.5).

Fig.4
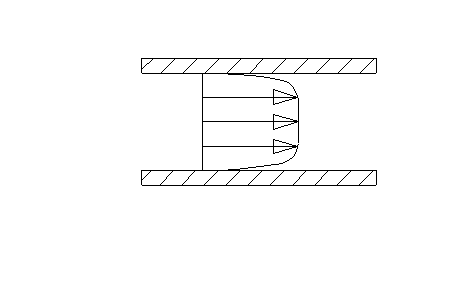
Fig.5
E’ possibile considerare il fluido suddiviso in tanti filetti che nel primo caso si muovono mantenendo sempre la propria individualità e quindi senza mai intersecarsi, mentre nel secondo caso si mescolano continuamente dando luogo alla formazione di vortici.
Nel primo caso la velocità varia nella sezione con legge parabolica del secondo ordine e, per condotti a sezione costante, è sempre diretta parallelamente all’asse del condotto. Anche nel secondo caso la velocità è maggiore vicino all’asse e decresce man mano che ci si avvicina alle pareti fino ad annullarsi in corrispondenza di esse, ma i profili sono decisamente più appiattiti.
Per valutare l’energia cinetica si ricorre quindi ad un opportuno valore medio della velocità ( W ), definito come quel valore ipotetico della componente della velocità parallela all’asse che, uniforme su tutta la sezione normale S, sarebbe in grado di dare la stessa portata in volume che si ha nella realtà
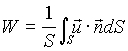 (10)
(10)
Con u si è indicato il valore locale della velocità.
La massa di fluido che nell’unità di tempo attraversa la generica sezione S del condotto è allora data dalla relazione
![]() (11)
(11)
considerando r costante su tutta la sezione.
Quando la velocità è diretta normalmante alla sezione, l’energia cinetica trasportata dalla massa di fluido nell’unità di tempo attraverso la sezione S è data da
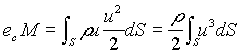 (12)
(12)
Dalle (11) e (12) si ha cosi’ che l’energia cinetica che compete all’unità di massa di fluido vale
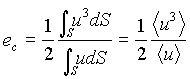 (13)
(13)
con
![]()
e
![]() .
.
Mentre il valor medio della velocità è sempre determinabile in funzione della portata con la (11), il valor medio del cubo della velocità è determinabile solo se si conosce come varia la velocità sulla sezione: tale risultato è ottenibile solo in casi particolarmante semplici.
Si scrive allora la (13) nella forma
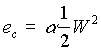 (14)
(14)
definendo così un coefficiente correttivo dato dalla relazione
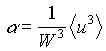 (15)
(15)
Il fattore a assume valori compresi tra 1 e 2. In particolare vale 1 nel caso di moto così turbolento da poter considerare un profilo di velocità piatto, con una velocità media uniforme sulla sezione, mentre vale 2 nel caso estremo di moto completamente laminare con profilo parabolico.
Quindi
![]() (16)
(16)
e
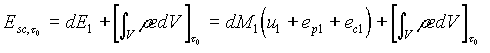 (17)
(17)
dove con e si è indicato genericamente il valore locale dell’energia specifica del sistema aperto, comprendendo in esso tutte le forme che essa può assumere (interna, cinetica, potenziale) e tenendo conto del fatto che può variare da punto a punto del sistema.
Le stesse considerazioni fatte per calcolare l’energia del sistema chiuso ausiliario al tempo t = t0 possono essere applicate per calcolare il contenuto energetico del sistema dopo un tempo di osservazione infinitesimo dt. Quindi all’istante t = t0 + dt, poichè il sistema chiuso è costituito, per quanto detto nel paragrafo relativo all’equazione di bilancio della massa, dalla massa contenuta nel sistema aperto più la massa dM2 che è appena uscita da esso, abbiamo
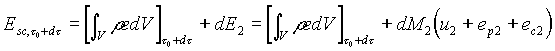 (18)
(18)
Supponendo che nell’intervallo di tempo dt sia possibile modificare il contenuto di energia del sistema chiuso solo per mezzo di scambi di energia con il contorno sotto forma di calore e di lavoro, possiamo applicare il I principio della termodinamica per i sistemi chiusi al sistema ausiliario
![]() (19)
(19)
Supponiamo di dividere il contorno del sistema chiuso in due porzioni: una comprendente la superficie laterale, l’altra le sezioni di ingresso e di uscita.
Quindi:
![]() (20)
(20)
e
![]() (21)
(21)
La quantità di calore che eventualmente viene scambiata per conduzione attraverso le sezioni è in genere trascurabile rispetto alla quantità che nel tempo dt attraversa la superficie laterale, quindi con buona approssimazione
![]() (22)
(22)
Passiamo all’analisi degli scambi di lavoro. Poiché le pareti laterali sono rigide ed indeformabili, normalmente si fa entrare ed uscire lavoro dal sistema tramite alberi rotanti. Poniamo allora il lavoro scambiato attraverso le pareti laterali uguale ad un generico contributo di lavoro meccanico dL.
Il lavoro Lsezioni è uguale al lavoro, compiuto dal fluido che si trova a monte e a valle del sistema chiuso, per introdurre nel sitema aperto la massa dM1 e per estrarre dallo stesso la massa dM2. Esso si calcola nel modo seguente.
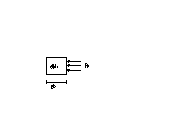
Fig.6
Il lavoro necessario per spingere nel sistema aperto la massa dM1 è uguale a
![]() (23)
(23)
dove dx è lo spostamento fatto nel tempo dt e F è la forza necessaria per contrastare la pressione, che chiamiamo P1, esercitata sulla massa dM1 dal fluido che si trova dentro al sistema aperto. Quindi se S è l’area della sezione
![]() (24)
(24)
E
![]() (25)
(25)
Ma Sdx = dV e dV = vdM1, quindi considerando i valori specifici otteniamo
![]()
![]() (26)
(26)
Questo è un lavoro di introduzione e viene ricevuto dal sistema quindi quando lo sostituiremo nell’equazione del bilancio dovremo considerarlo con segno negativo.
Analogamente possiamo calcolare il lavoro compiuto (darà quindi un contributo positivo) dal fluido del sistema aperto sulla massa dM2.
![]() (27)
(27)
Sostituiamo le espressioni (22), (26), (27) nella (19)
![]() (28)
(28)
Usiamo la (17) e la (18) e otteniamo la (29)
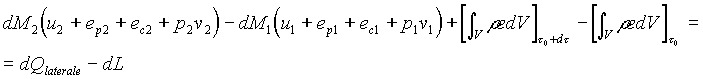
Se dividiamo entrambi i membri per dt e utilizziamo l’espressione dell’entalpia otteniamo l’equazione finale di bilancio dell’energia per unità di tempo (è quindi più propriamente un bilancio di potenze) per il sistema aperto
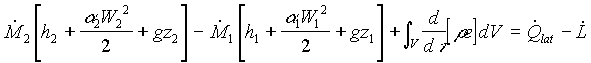 (30)
(30)
Questa equazione vale nel caso generico di regime transitorio. Supponendo invece che il sistema sia in regime stazionario abbiamo che l’integrale si annulla e che, per l’equazione di bilancio della massa ,![]() . Dividendo allora entrambi i membri della (30) per
. Dividendo allora entrambi i membri della (30) per ![]() otteniamo l’equazione di bilancio dell’energia nella sua forma canonica
otteniamo l’equazione di bilancio dell’energia nella sua forma canonica
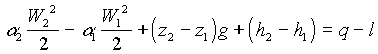 (31)
(31)