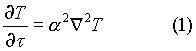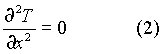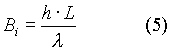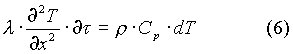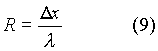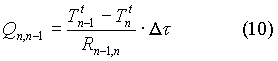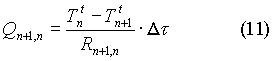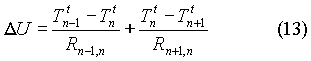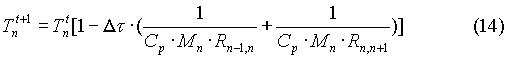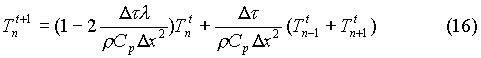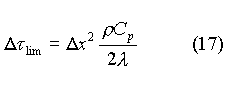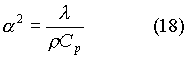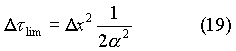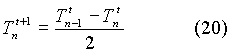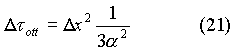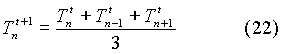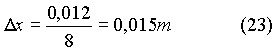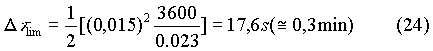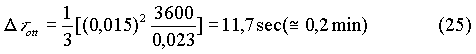
Anno accademico 1999-2000

Corso di laurea : ingegneria elettronica

Corso di fisica tecnica

Docente del corso : prof. Angelo Farina
 
 

Giovanna Chizzoni – matricola 88385

Lezione del 10/01/2000 16:30 – 18:30

                                                              TRANSITORIO TERMICO
 
 
 

  

 1. INTRODUZIONE

In campo ingegneristico, lo studio e la risoluzione di quesiti viene affrontato attraverso un’analisi matematica che purtroppo si discosta dalla richiesta delle soluzioni dei problemi affrontati quotidianamente.

Un’analisi reale di tutte le proprietà che descrivono il sistema , generalmente, si presenta in maniera troppo complicata e per la maggior parte dei casi irresolubile.

Anche lo Scambio Termico in regime stazionario, a causa delle complessità delle condizioni di contorno (non uniformità della temperatura, superfici irregolari, trattazioni bi-tridimensionali), non consente di utilizzare una soluzione analitica, ma richiede l’uso dell’equazione di Fourier alle differenze finite.
 
 

2. TRATTAZIONE NUMERICA FINITA

Il transitorio termico, cioè l’evoluzione nel tempo del sistema, è analizzabile con rigore dall’equazione di Fourier :


 
 

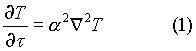
In regime stazionario, la forma dell’equazione di Fourier applicata ad una lastra monodimensionale si riduce a


 

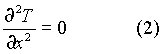
 Nel transitorio termico, invece, non sono più trascurabili i termini temporali ma si evidenzia una dipendenza tra la temperatura e il tempo .

Per via analitica questa relazione non é esplicabile .Per far fronte a queste difficoltà ci si limita a studiare le soluzioni numeriche attraverso due metodologie differenti :
 

A-ELEMENTI FINITI
B-DIFFERENZE FINITE
 

 2.A ELEMENTI FINITI

Questo metodo non viene analizzato per la sua complessità, infatti solo una variabile é discretizzata, l’altra rimane in forma continua .
 
 

2.B DIFFERENZE FINITE

Questo metodo é facilmente eseguibile su un foglio di calcolo di tipo excel. Si basa su una discretizzazione dello spazio geometrico utilizzando celle regolari.


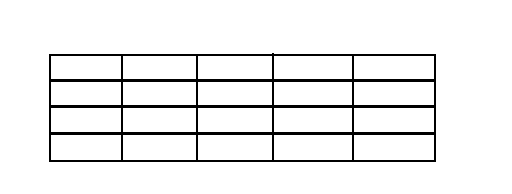
Fig. 1- esempio di suddivisione di uno spazio in celle regolari.






Risulta facilmente spiegabile l’associazione di una matrice con i suoi elementi ad una lastra piana suddivisa in modo regolare da celle ,chiamate nodi, che contengono informazioni riguardanti la massa o la temperatura .

Il metodo delle differenze finite fa ricorso alla discretizzazione di tutte e due le variabili; viene di seguito riportata la trattazione di un transitorio termico, che non essendo risolvibile analiticamente, utilizza questo metodo.
 
 

3.TRANSITORIO TERMICO DI UNA LASTRA INDEFINITA

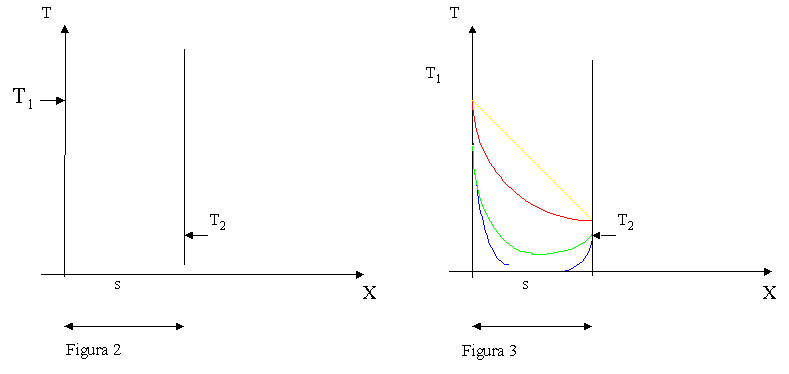
Una lastra piana indefinita di materiale omogeneo, inizialmente si trova in una situazione indisturbata, cioè:
 
 

La lastra viene poi immersa in un liquido a temperatura diversa, T diversa da T0 ,di conseguenza , si ha un rapido assestarsi della temperatura di pelle interna T1(x = 0) e della temperatura di pelle esterna T2(x = S).

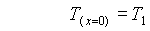
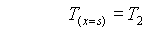
In figura due é rappresentata la propagazione istantanea della temperatura sulle pareti della lastra.

In figura tre é rappresentato l’andamento di T (x ) per diversi istanti di tempo.
 
 
  Si deve calcolare la funzione 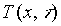, non trascurando però le seguenti condizioni di contorno :
 
 

- h = coefficiente di convezione.

- L = lunghezza caratteristica del problema( s/2 : semispessore ).

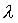- = conducibilità termica del materiale della lastra.
 
 

Per valori di Bi < 0,1, il transitorio é di tipo convettivo . La conducibilità é così elevata che l’intera lastra raggiunge istantaneamente la temperatura del fluido di immersione ( é trascurabile la dipendenza da x ).

Per valori di Bi > 40, l’ipotesi di rapidità della temperatura é accettabile, spariscono i coefficienti di convezione, il transitorio é di tipo conduttivo e si analizza con l’equazione di Fourier nella forma monodimensionale :
 
 

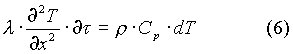
        - Cp = calore specifico a pressione costante - 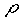= densità del liquido

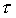- = tempo
 
 

L’equazione di Fourier scritta in questi termini rappresenta il primo principio della termodinamica : la quantità di calore scambiata in un tempo infinitesimo uguaglia la variazione di energia interna.

Questa espressione é risolvibile discretizzando x e .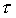
 

4. DISCRETIZZAZIONE SPAZIALE

Si suddivide la lastra in una serie di fette, tutte a temperatura uniforme. Ciascuna di queste fette, conduttrici di calore, é collegata ad un altra tramite un nodo.

Il primo nodo é situato sulla pelle interna della lastra, di seguito gli altri fino all’ultimo, situato sulla pelle esterna.
Tutti i nodi sono distanziati di un valore .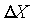
La variabile x risulta così discretizzata :

  

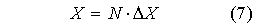
- x = variabile discreta

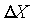-  = passo spaziale

- N = indice di nodo [o¸ n]

In realtà il numero di nodi é n+1 invece il numero di divisioni é n.
 

5.DISCRETIZZAZIONE TEMPORALE

Similmente a quanto detto sopra, si deve discretizzare anche il tempo 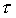, considerando un opportuno intervallo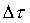 

 La variabile t risulta così discretizzata :

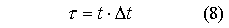
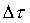- = passo temporale

- t = indice temporale
 
 

6. EQUAZIONE DI FOURIER ALLE DIFFERENZE FINITE
 

Mediante l’equazione di Fourier alle differenze finite, applicata ad un generico strato della lastra, si vuole trovare a partire dal tempo attuale la temperatura al tempo successivo: siamo di fronte ad un transitorio termico.

Per semplicità, la resistenza termica tra due nodi consecutivi, n-1 e n, si può rappresentare con una resistenza elettrica R di valore

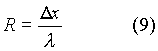
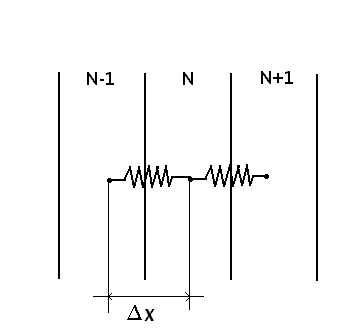
Fig. 4 - Lastra suddivisa in generici strati collegati da nodi






La quantità di calore scambiata tra il generico nodo n e il suo nodo precedente n-1 al tempo attuale t è :

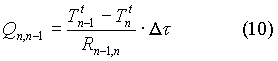
- T n-1 t = temperatura attuale del generico nodo n-1

- T n t = temperatura attuale del generico nodo n

- R n-1,n = resistenza tra il nodo n ed il nodo n-1
 

Lo stesso calcolo si può fare per il generico nodo n+1, quindi
 
 


 
 

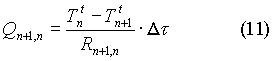
Avendo già evidenziato l’analogia dell’equazione di Fourier con il 1° principio della termodinamica risulta facile capire che la variazione di energia interna si può esprimere nel seguente modo :
 
 


 

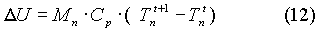
- M n= massa del nodo n
- Tn t+1 =temperatura del nodo n al tempo t+1

 
  A questo punto uguagliando la variazione di energia interna con la somma della quantità di calore scambiata tra il nodo n e i suoi nodi adiacenti, si nota che l’unica incognita presente è la temperatura del nodo n al tempo futuro t+1
 


 
 


 
 

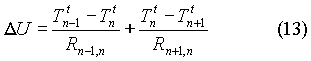
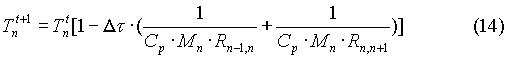
La nuova temperatura del nodo ennesimo è una combinazione lineare della temperatura dei nodi limitrofi all’istante attuale, cioè
 


 

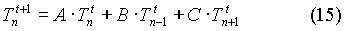
A,B,C = costanti reali

Questo metodo di evoluzione temporale, detto Time Marcing, presenta delle limitazioni, infatti non è possibile prevedere i valori futuri delle temperature al di sopra di un certo 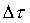limite.

Per ricercare questo valore limite si consideri

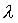-= costante

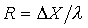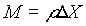         - -( M = massa del generico nodo)

si ottiene la nuova formula
 
 

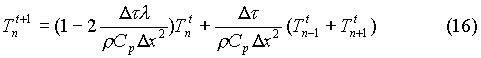
Se il termine che moltiplica Tntdiventasse negativo si sarebbe di fronte ad una contraddizione del primo principio della termodinamica ; il nodo n avrebbe temperature inferiori ai nodi adiacenti e ciò renderebbe instabile la soluzione e inaccettabile il fenomeno dal punto di vista energetico. Il valore che annulla tale termine è definito passo temporale limite.

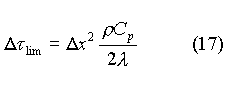
Ma avendo definito la diffusività termica come
 


 

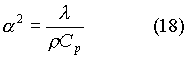
si ottiene
 


 

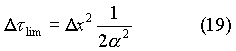
Dall’ultima formula si vede che il passo temporale è legato al passo spaziale e alle caratteristiche del materiale.

Utilizzando 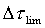, la formula risolutiva diventa una media matematica
 


 

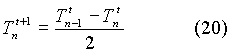
Si può ottenere una soluzione migliore, ma più lenta, utilizzando il passo temporale ottimale
 


 

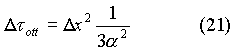
In questo ultimo caso la formula risolutiva diventa
 


 
 

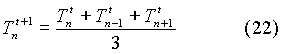
7. ESEMPIO

Una lastra piana indefinita ha spessore s = 120 mm, diffusività 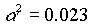 m2/h e temperatura iniziale T0 = 38° C.
La lastra viene poi immersa nell’olio alla temperatura T1 = 260° C.

Si vuole calcolare 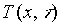 nei primi tre minuti.
 
 

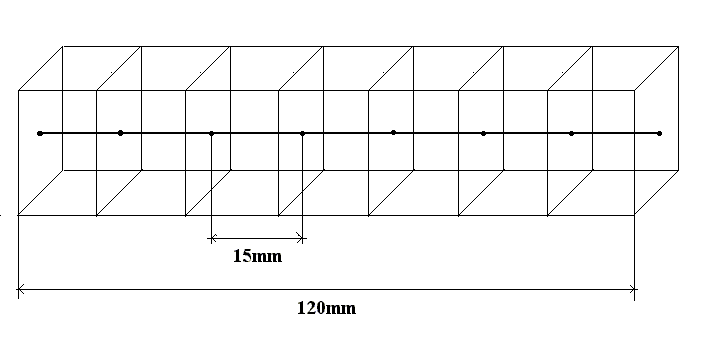
Fig.5-lastra divisa in celle


Istantaneamente tutta la lastra a contatto con l’olio caldo raggiunge la temperatura del liquido .

Si considerino, ad esempio, 8 nodi
 
 


 


 
 

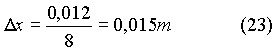
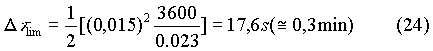
Ci sono dunque 11 intervalli di tempo dove calcolare le temperature dei nodi.

Costruiamo una tabella con le temperature dei primi cinque nodi. La temperatura del nodo n al tempo t +1 è la media aritmetica delle temperature dei nodi adiacenti al tempo precedente t . Al tempo iniziale tutti i nodi sono alla temperatura T0, dopo l’immersione il calore si diffonde lungo tutta la lastra .
 
 
               
Min t 0 1 2 3 4 5
0 0 38 38 38 38 38 38
0,3 1 260 38 38 38 38 38
0,6 2 260 149 38 38 38 38
0,9 3 260 149 94 38 38 38
1,2 4 260 177 94 66 38 66
1,5 5 260 177 122 66 66 66
1,8 6 260 191 122 94 66 94
2,1 7 260 191 143 94 94 94
2,4 8 260 202 143 119 94 119
2,7 9 260 202 161 119 119 119
3 10 260 211 161 140 119 140
Fig. 5







In figura cinque sono stati riportati solo cinque nodi , infatti per ovvie ragioni di simmetria , la prima metà della lastra (quattro nodi ) si comporta come la seconda .

La presenza del quinto nodo evidenzia questa situazione , infatti i suoi valori sono uguali a quelli del terzo nodo .
 
 
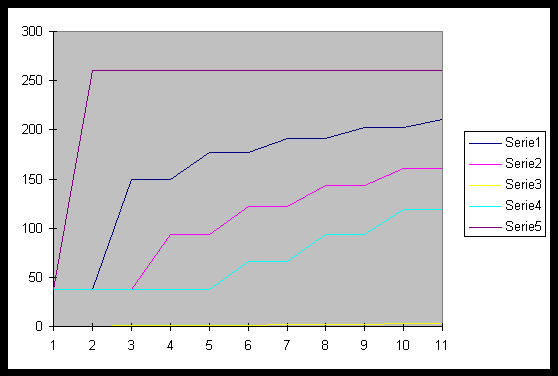Fig.6








In figura 6 è stato riportato l’evolversi della temperatura lungo i nodi.

I gradini presenti nel grafico sono un artefatto, in realtà il processo è continuo. Si sarebbero evitate queste imprecisioni utilizzando il passo temporale ottimale
 


 

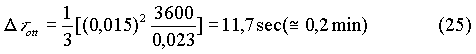
Con il passo temporale ottimale è possibile costruire una tabella simile a quella precedente ma con 15 intervalli di tempo .
 
 
 
 
               
Minuti
t
0
1
2
3
4
5
0
0
38
38
38
38
38
38
0,2
1
260
38
38
38
38
38
0,4
2
260
112
38
38
38
38
0,6
3
260
137
63
38
38
38
0.8
4
260
153
79
46
38
46
1
5
260
164
93
54
43
54
1,2
6
260
172
104
63
50
63
1.4
7
260
179
113
72
59
72
1.6
8
260
184
121
81
68
81
1.8
9
260
188
129
90
77
90
2
10
260
192
136
99
86
99
2.2
11
260
196
142
107
95
107
2.4
12
260
199
148
115
103
115
2.6
13
260
202
154
122
111
122
2.8
14
260
205
159
129
118
129
3
15
260
208
164
135
125
135
Fig.7

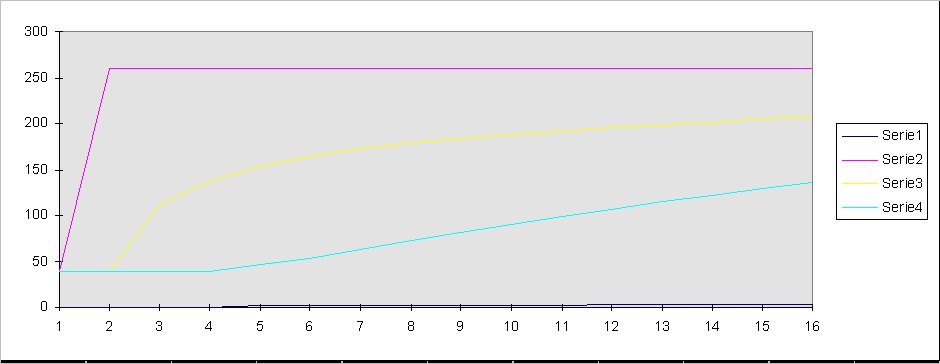
Fig.8

La scelta del passo temporale ottimale si è rivelata la migliore, infatti anche il grafico in figura 8 presenta tratti lineari e continui che descrivono quindi meglio la situazione reale del transitorio.

Con le basi di teoria finora presentate è possibile realizzare un programma, per esempio in qbasic, capace di risolvere il problema del transitorio termico precedentemente citato.