Transitori termici
Vi sono 2 metodi per trovare questa soluzione numerica:
- metodo alle differenze finite
- metodo agli elementi finiti.
Il primo metodo presenta si il notevole vantaggio di essere concettualmente semplice e quindi alla portata di tutti, visto che è eseguibile direttamente a partire da un foglio di calcolo elettronico con un normalissimo computer, ma ha anche alcune limitazioni.
Il metodo agli elementi finiti, invece, è molto più potente, ma anche molto più difficile, tanto da dover richiedere, in alcuni ambiti, un corso a sé stante.
Analizziamo quindi il metodo alle differenze finite premettendo però che, per semplicità di calcoli e senza nulla togliere all’esattezza dei risultati, porteremo avanti l’analisi del problema di transitorio termico in un caso unidimensionale, in modo che le varie funzioni che dovremo analizzare, quali la temperatura del corpo o il calore scambiato, possano essere considerate come funzioni della sola variabile spaziale x.
Questo metodo si basa su di una discretizzazione geometrica della geometria del problema, cioè su di una suddivisione regolare del problema geometrico in celle elementari: si passa quindi ad una rappresentazione matriciale del nostro problema.

Figura 1 - Rappresentazione matriciale del problema
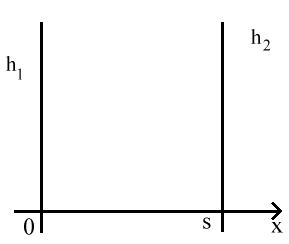
Figura 2 - Schematizzazione della lastra di spessore s
Quindi, una volta immersa nell’olio, la temperatura della pelle per x = 0 arriverà ad un certo valore, mentre per x = s assumerà un altro valore, in generale diverso dal precedente:
-
-
Si assisterà quindi ad un progressivo avanzamento del fronte di temperatura
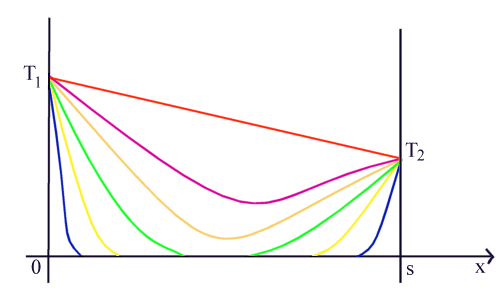
Figura 3 - Avanzamento del fronte di temperatura T(x)
Quello che noi cerchiamo ora è
Oss. Perché ci sia rapidità di adattamento della temperatura della lastra una volta immersa nel liquido è necessario che il coefficiente di convezione sia il più alto possibile. Per essere sicuri che le ipotesi da cui siamo partiti (istantaneità di adattamento della pelle della lastra alla temperatura dell’olio) siano corrette e si possano così ottenere risultati con errori accettabili si deve guardare il numero di Biot, definito come:
(1)
- h, è il coefficiente di convezione
- L, è la lunghezza caratteristica (nel nostro caso è lo spessore della lastra che deve essere percorso prima di arrivare al "nocciolo" vero e proprio del problema cioè, data la simmetria, lo spessore s/2)
-
Se
se
Mettiamoci allora nel primo caso e studiamo un transitorio conduttivo (è come se supponessimo
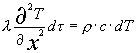
(2)
Per risolvere analiticamente questa equazione si dovrebbe procedere per approssimazione con uno sviluppo in serie di funzioni arrestate ad un certo punto; risolviamolo allora con il metodo delle differenze finite e discretizziamo, come richiesto, entrambe le variabili
Per prima cosa operiamo la discretizzazione spaziale che consiste in una suddivisione della lastra in una serie di strisce e concentriamo tutta la nostra attenzione sui soli punti centrali di queste. Questi punti, chiamati nodi, hanno la particolarità che in essi è concentrata tutta la temperatura della striscia corrispondente, potendo così trascurare tutto quello che succede tra un nodo e l’altro. Si parte ponendo un nodo sulla prima pelle e si procede poi a passo costante
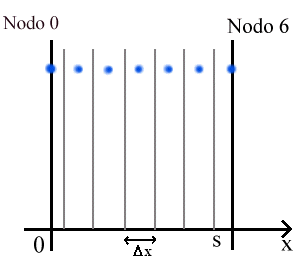
Figura 4 - Discretizzazione spaziale
Nel nostro caso ci sono 7 nodi, numerati 0,1,2,3,4,5,6 e quindi il numero di divisioni sarà 6 (n° divisioni = n° nodi - 1); la prima e l'ultima striscia hanno spessore
Per la discretizzazione temporale si deve adottare un opportuno passo temporale
(3)
Ora possiamo riscrivere l’equazione di Fourier alle differenze finite; prendiamo un generico strato n-esimo intermedio (n = 0,1,2,…,N) e calcoliamo lo scambio termico tra gli strati adiacenti ricordando che, se rappresentiamo il modello con il circuito elettrico equivalente, i tre strati saranno connessi da opportune resistenze termiche in serie.
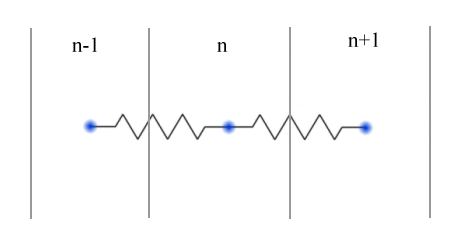
Figura 5 - Rappresentazione con resistenze termiche equivalenti in serie
Ad un tempo intermedio t (cioè t volte
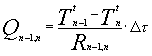
(4)
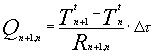
(5)
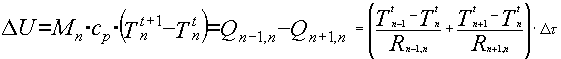
(6)
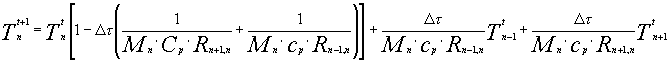
(7)
Si vede quindi che la temperatura al tempo futuro è una combinazione lineare della temperatura, all'istante attuale, del nodo attuale, di quello precedente e di quello successivo:
(8)
(9)
(10)
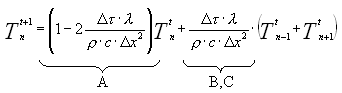
(11)
Quindi il transitorio può essere risolto tramite questa tecnica, detta “TIME MARCHING”, che ci permette di dedurre le temperature al tempo futuro partendo da quelle al tempo attuale: iterando il ragionamento fino alla situazione stazionaria si trova la soluzione del problema.
Oss. Un notevole limite di questo metodo è, però, che non riesce a vedere più in là di un nodo: non si può quindi sperare di poter prevedere il futuro, partendo dal solo presente, perché non si hanno dati a sufficienza.
Più la discretizzazione è fina più il passo temporale è piccolo, tuttavia non si può andare oltre un certo
Per trovare il passo temporale limite si uguaglia ora a zero il coefficiente A:
(12)
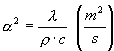
la diffusività termica (che rappresenta la rapidità di propagazione delle variazioni di temperatura nel materiale).
Quindi il
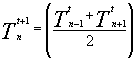
(13)
che è la media aritmetica tra le temperature dei nodi adiacenti.
Di solito però conviene scegliere il
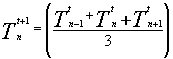
(14)
dove ho ridotto il passo temporale e quindi devo eseguire un maggior numero di calcoli.
Esercizio.
Consideriamo una piastra di spessore
e diffusività
alla temperatura iniziale di 38 °C che viene immersa istantaneamente in olio bollente alla temperatura di 260 °C.
Trovare

Consideriamo 9 nodi (allora N=8)
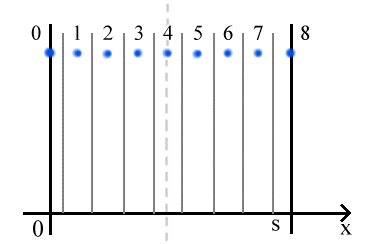
Figura 6 - Discretizzazione geometrica della piastra
Il passo spaziale sarà :
(15)
(16)
Essendo il transitorio da studiare di 3 minuti e il passo temporale di 0.3 minuti dovremo compiere 10 passi. Supponendo che la pelle abbia un tempo d'inerzia trascurabile (allora
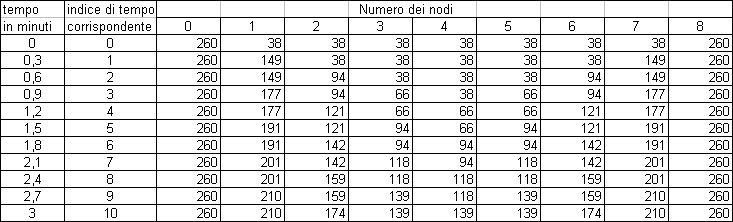
Figura 7 - Tabella di propagazione delle temperature
Poiché la piastra viene immersa istantaneamente, tanto il nodo 0 quanto quello 8 si troveranno subito alla stessa temperatura di 260 °C, mentre i nodi intermedi rimarranno, inizialmente, alla temperatura di 38 °C; poi con il passare del tempo la temperatura aumenterà dall'esterno della piastra verso l'interno in modo simmetrico: per questo motivo i nodi 1 e 7, 2 e 6, 3 e 5, assumono gli stessi valori.
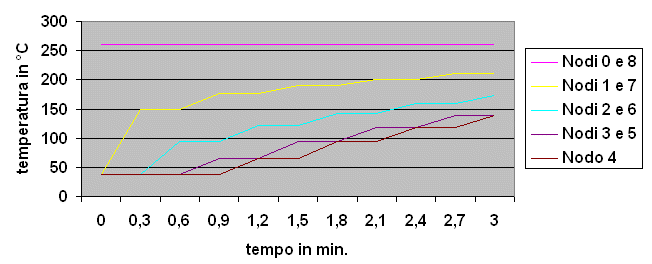
Figura 8 - Andamento delle temperature nei nodi 3 e 5
Guardando il grafico sembrerebbe quasi di trovarci di fronte ad un processo un po’ particolare che parte da un certo valore, poi sale un po’, quindi si ferma e dopo un certo tempo aumenta ancora, proprio come in un processo “discreto”; in realtà il processo è continuo: i gradini sono dovuti al fatto che abbiamo usato il passo temporale limite; se avessimo usato il passo temporale ottimale avremmo dovuto eseguire un numero di calcoli maggiore ma avremmo ottenuto un grafico con curve più morbide.