Università degli studi di Parma
Facoltà di ingegneria Elettronica
Corso di FISICA TECNICA
Docente: Angelo Farina
Anno Accademico1999/2000
Lezione riguardante la sezione del corso relativa alla termodinamica
PROPRIETA’ DELLE SOSTANZE CHIMICAMENTE PURE
Abbiamo visto che per poter studiare le sostanze chimicamente pure necessitavamo del diagramma termodinamico (p, v) che ci permetteva di valutare l’andamento delle variabili di stato quali pressione p e volume v in corrispondenza di particolari temperature alle quali la sostanza si trova.

– Diagramma termodinamico
Avevamo successivamente notato che tale diagramma poteva essere suddiviso in 4 zone (vedi figura) , e precisamente:
Ciascuna zona vedremo poi essere caratterizzata da particolari equazioni che ci permetteranno determinare le coordinate termodinamiche (quali volume, energia interna, entropia e entalpia) a noi incognite, una volta note pressione e temperatura. Notiamo che tali variabili (p, T) sono ovunque indipendenti eccetto che nella zona dei vapori saturi dove la T è costante con la pressione.
In generale a noi non interessa sapere quello che accade al di sotto dell’isoterma corrispondente ai 0°C, in quanto in tali condizioni l’acqua solidifica e lo stato solido a noi non interessa studiarlo.
LIQUIDO
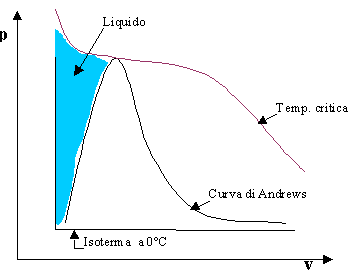
Il liquido è uno stato intermedio tra lo stato gassoso e quello solido. Nel diagramma termodinamico esso si trova nella zona compresa fra l’isoterma critica (al di sopra della quale non è possibile avere la fase liquida) e alla sinistra della curva di Andrews.
Si nota che in tale regione abbiamo delle rette che possiamo considerare verticali e che esplicitano la relazione tra pressione e volume al variare della temperatura. Questo significa che il volume è indipendente dalla pressione, ovvero possiamo considerare il liquido incomprimibile.
Per tale regione non esistono formule e la dipendenza v=v(T) è tabulata su tabelle, dove però non compare il volume, ma la densità definita come il reciproco del volume:![]() le cui dimensioni sono kg/m3 (massa per unità di volume).
le cui dimensioni sono kg/m3 (massa per unità di volume).
Le altre proprietà quali energia interna, entalpia e entropia, si ricavano dal calore specifico.
Essendo il volume indipendente dalla pressione si ha che il cp=cv , quindi si è soliti indicare tale quantità con cL(T): da notare però la dipendenza dalla temperatura, ma la non dipendenza dalla trasformazione precedentemente eseguita.
A questo punto siamo in grado di definire u, h e s. Lavorando tra due stadi 1 (iniziale) e 2 (finale) che si trovano a due temperature molto diverse, si ottiene:
![]()
dove cLmedio è il calore specifico medio relativo alle due temperature alle quali si opera.
Apriamo a tale proposito una parentesi sul calcolo di tale valore.
In tale caso si usano in genere:
* MEDIA LINEARE
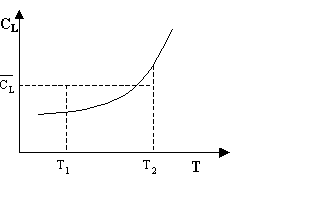
La media lineare è definita come:
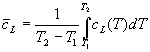
e che graficamente corrisponde a quel valore tale per cui l’area del rettangolo, che ha per altezza tale valore e per base il D T, è uguale a quella sottesa dalla curva tra le stesse temperature.
* MEDIA LOGARITMICA
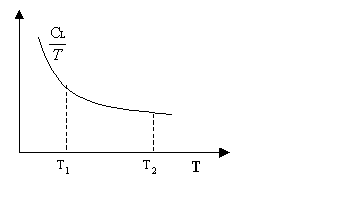
La media logaritmica definita come :
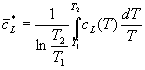
e che graficamente corrisponde a quel valore che moltiplicato per il logaritmo naturale del
rapporto tra le temperature, fornisce l'area sottesa dalla curva.
Quando però CL varia poco con la temperatura i due valori tendono a coincidere.
L’entalpia invece è definita come:
![]()
ovvero il salto di energia interna coincide con quello dell’entalpia.
Questo paradosso lo si può giustificare se andiamo a considerare la definizione di entalpia. Questa infatti risulta essere: h=u + pv, quindi ponendo u=h non si fa altro che trascurare il termine pv.
Tale approssimazione a volte può portare a degli assurdi. Consideriamo come esempio una pompa centrifuga in cui il fluido entrante ha le seguenti proprietà : p1=1 bar, v1=0,001 m3/kg, T1=20 °C, mentre quello di uscita ha : p2=10 bar, v2=0,001 m3/kg, T2=20°C.
Essendo il salto di temperatura nullo allora u2-u1=0. Secondo la formula soprastante si avrebbe anche che h2-h1=0, ma il salto di entalpia non può essere nullo altrimenti non riusciremmo a spiegarci la sparizione del lavoro meccanico compiuto dalla pompa (p*v), in netto contrasto con il principio di conservazione dell’energia.
Possiamo quindi precisare che la formula adottata in precedenza è vera se la temperatura non è infinitesima, altrimenti dobbiamo utilizzare la seguente relazione:
![]()
Passiamo ora al calcolo dell’entropia.
Ricordiamo che dalla definizione di calore specifico ed essendo cp = cv = cL si ha: ![]() e quindi dalla definizione di entropia:
e quindi dalla definizione di entropia:
![]() ,
,
che integrato tra lo stato iniziale e quello finale mi da la variazione dell’entropia ricercata
![]()
tenendo conto che il calore specifico che compare è calcolato utilizzando la media logaritmica, definita prima, tra i due calori specifici delle due temperature ( T1 e T2 ) alle quali si opera.
GAS PERFETTO
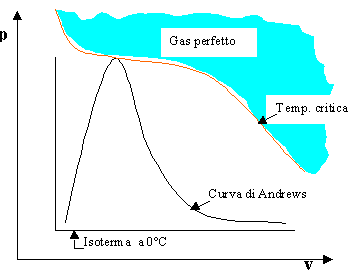
I gas perfetti, nel diagramma termodinamico sono situati nella zona al di sopra dell’isoterma critica, dove l’equazione che descrive l’andamento di v in funzione di p assume assume un andamento che si avvicina a quello di un’iperbole equilatera, come si può notare dalla figura.
In tal caso vale quindi l’equazione dei gas perfetti:
pv=RT
(che è proprio l’equazione di un’iperbole). P è la pressione del gas, v è il volume specifico espresso in Kg/m3, T è la temperatura espressa in Kelvin e R è una costante che dipende dal gas considerato e che si ottiene dalla costante universale R0 dividendola per la massa molare del gas in esame: ![]() . R0 vale 8314 J/kmoliK. Per l’aria Raria=287 J/kgK.mentre per l'acqua R=462 J/kgK.
. R0 vale 8314 J/kmoliK. Per l’aria Raria=287 J/kgK.mentre per l'acqua R=462 J/kgK.
Per quel riguarda il volume specifico si ricava direttamente dall’equazione di stato e vale
![]()
Si trova che solo per i gas perfetti vale la relazione seguente tra il calore specifico a pressione costante e quello a volume costante
![]()
Si definisce poi la grandezza g come
![]()
che è un numero puro perché rapporto di grandezze con le stesse dimensioni.
La seguente tabella mostra le capacità termiche molari di alcuni gas:
|
Gas |
Cp (J/moleK) |
Cv (j/moleK) |
Cp - Cv(j/moleK) |
g |
|
Monoatomici |
||||
|
Ideale |
20.8 |
12.5 |
8.3 |
1.67 |
|
He |
20.8 |
12.5 |
8.3 |
1.66 |
|
Ar |
20.8 |
12.5 |
8.3 |
1.67 |
|
Biatomici |
||||
|
Ideale |
29.1 |
20.8 |
8.3 |
1.40 |
|
H2 |
28.8 |
20.4 |
8.4 |
1.41 |
|
N2 |
29.1 |
20.8 |
8.3 |
1.40 |
|
O2 |
29.4 |
21.1 |
8.3 |
1.40 |
|
Poliatomici |
||||
|
Ideale |
33.3 |
24.9 |
8.3 |
1.33 |
|
Co2 |
37.0 |
28.5 |
8.5 |
1.30 |
|
NH3 |
36.8 |
27.8 |
9.0 |
1.31 |
Notiamo che la grandezza g rappresenta l’esponente nella trasformazione isoentropica (s=Kost) e precisamente:
![]()
Avendo a disposizione queste relazioni faccio senza avere tabulati i cp e cv ,, basta conoscere il tipo di molecola e la sua massa atomica (che si ricava una volta nota la sua formula).
La teoria dei gas è una delle poche che trova riscontro nella realtà.
Utilizziamo il primo principio della termodinamica per ricavare le altre coordinate termodinamiche: ![]() .
.
Essendo poi l’energia interna una variabile di stato e che quindi non dipende dal percorso seguito, ma solo dai valori iniziali e finali, prendo una trasformazione a volume costante e una a temperatura costante per passere dallo stato iniziale 1 a quello finale 2.
Con la legge di Joule si ha che u=u(T) e h=h(T), ovvero energia interna e entalpia dipendono solo dalla temperatura e non da pressione e volume.
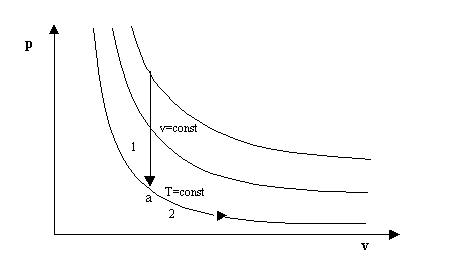
In tal caso la variazione di energia interna si avrà solo nella trasformazione a v costante (da 1 ad a) e quindi
![]()
e siccome avevamo detto che il calore specifico non dipende dalla temperatura, integrando otteniamo
![]()
Prendo poi l’altra forma del primo principio:
![]()
Anche in questo caso l’entalpia è una funzione di stato indipendente e quindi analogamente a prima posso scegliere un qualsiasi cammino per congiungere lo stato iniziale con quello finale, tanto la variazione è la stessa. A tale proposito scelgo prima una trasformazione a p costante e poi una isoterma.
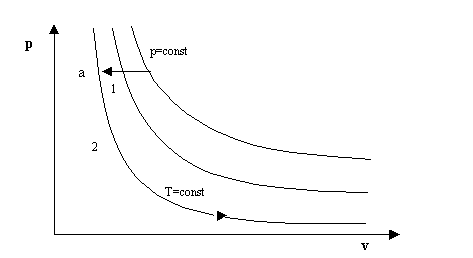
Sempre dalla legge di Joule ho che lungo l’isoterma non ho variazione di entalpia, che invece ho sul tratto a p Kost (da 1 a a).
Quindi ![]() e integrando
e integrando ![]() .
.
Per avere espressioni dell’energia interna e dell’entalpia assolute, posso considerare nulle l’entalpia e l’energia interna del gas alla temperatura di 0°C, che utilizzo quindi come riferimento (u0=0 ; h0=0). In tal modo si ha:
![]()
![]()
Possiamo quindi avere valori negativi.
Per calcolare l’entropia specifica si può procedere in due modi diversi utilizzando l’una o l’altra forma del primo principio. Sviluppiamole parallelamente:
|
|
|
|
|
|
|
|
|
|
Usando l’equazione di stato pv=RT e sostituendo rispettivamente |
|
|
|
|
|
Otteniamo |
|
|
|
|
|
E integrando tra lo stao iniziale 1 e quello finale 2 : |
|
|
|
|
Le due formulazioni dell’entropia sono equivalenti e da queste se ne può ricavare una terza in funzione della coppia pv. A tale proposito utilizziamo la legge di stato nella forma T=pv/R:
![]()
Ricaviamo quindi la formula della curva isoentropica pvg =Kost definita precedentemente, ricordando che in tali curve deve essere D s= s2-s1=0. A tal scopo utilizziamo la formula dell’entropia in funzione della coppia pv.
![]()
Manipolando la formula con le proprietà dei logaritmi, si ha:
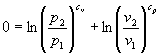 e quindi
e quindi 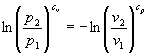
Siccome l’uguaglianza tra logaritmi equivale all’uguaglianza tra gli argomenti degli stessi otteniamo:
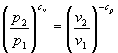
Ed estraendo la radice cv-esima
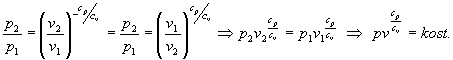
Essendo poi ![]() si ottiene l’equazione dell’isoentropica.
si ottiene l’equazione dell’isoentropica.
VAPORI SATURI
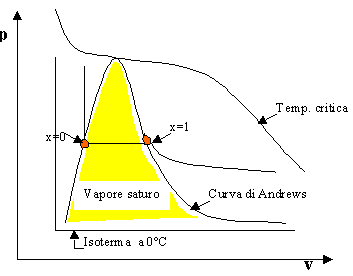
I vapori saturi si trovano nella zona compresa dalla curva di Andrews. In tale zona non abbiamo a disposizione una teoria generale, cioè non possiamo descrivere mediante equazioni l’andamento di p,v e T; ci si basa allora su dei dati sperimentali. Le soluzioni verranno quindi trovate per tentativi in quanto non si riescono a mettere delle tabelle nelle equazioni.
Entrando più nel dettaglio possiamo notare che abbiamo a disposizione due punti caratteristici: la stato del liquido e quello del gas che si trovano sul confine di separazione tra due zone. Ci si appoggia quindi sulle equazioni dei due stati appena analizzati: sul confine tra due zone le proprietà della sostanze sono definite.
Per calcolare le coordinate termodinamiche degli stati intermedi (cioè quelli tra liquido e vapore seguendo l’isoterma) si utilizza il titolo definito come:
![]() , quindi è una grandezza che varia tra 0 e 1.
, quindi è una grandezza che varia tra 0 e 1.
Sulle tabelle troviamo quindi i valori delle proprietà relative al liquido il cui titolo vale x=0 e del vapore avente x=1. Quindi la corrispondente proprietà del vapore saturo (0<x<1) si ricava a partire dal titolo mediante un iterpolazione lineare della stessa proprietà relativa ai due stati tabulati.
In particolare se vogliamo calcolare il volume specifico, dobbiamo innanzitutto definire il volume specifico differenziale ![]() , che assieme al volume specifico del liquido, tabulati entrambi, costituiscono i dati per ricavare v(x) (volume in funzione del titolo).
, che assieme al volume specifico del liquido, tabulati entrambi, costituiscono i dati per ricavare v(x) (volume in funzione del titolo).
![]() .
.
In alternativa potremo avere tabulati vl e vv da cui si ricava successivamente il vd.
In modo analogo verranno calcolate le altre proprietà :
![]()
![]()
![]()
Spesso però sulle tabelle dei vapori saturi troviamo solo alcune grandezze e precisamente p, Te hd in quanto le proprietà relative al liquido le posso ricavare a partire dalle considerazioni fatte precedentemente perché ci troviamo sì sulla curva limite, ma ancora di liquido si tratta.
Inoltre possiamo calcolarci l’energia interna differenziale e l’entalpia differenziale a partire da:
![]()
![]()
Poniamo poi hd =r e lo chiameremo calore latente di vaporizzazione per motivi storici.
Riporto di seguito alcuni valori del vapore d’acqua saturo.
|
Temp °C |
Press. (kPa) |
Volume specifico (m3/kg) |
Energia interna specifica (kJ/kg) |
Entalpia specifica (kJ/kg) |
Entropia specifica (kJ/kg) |
|||||||
|
Ts |
Ps |
Vl |
Vg |
Ut |
Ud |
Ug |
Hl |
Hd |
Hg |
Sl |
Sd |
Sg |
|
0 |
0.611 |
0.001 |
206.1 |
0.00 |
2375 |
2375 |
0.01 |
2501 |
2501 |
0.00 |
9.156 |
9.156 |
|
5 |
0.872 |
0.001 |
147.1 |
20.97 |
2361 |
2382 |
20.98 |
2489 |
2510 |
0.076 |
8.949 |
9.025 |
|
10 |
1.227 |
0.001 |
106.3 |
42.00 |
2347 |
2389 |
42.01 |
2477 |
2519 |
0.151 |
8.749 |
8.900 |
|
15 |
1.705 |
0.001 |
77.93 |
62.99 |
2333 |
2396 |
62.99 |
2465 |
2528 |
0.224 |
8.556 |
8.781 |
|
20 |
2.339 |
0.001 |
57.79 |
83.95 |
2519 |
2402 |
83.96 |
2454 |
2538 |
0.296 |
8.370 |
8.667 |
|
25 |
3.169 |
0.001 |
43.36 |
104.8 |
2304 |
2409 |
104.8 |
2442 |
2547 |
0.367 |
8.190 |
8.558 |
|
30 |
4.246 |
0.001 |
32.89 |
125.7 |
2290 |
2416 |
125.7 |
2430 |
2558 |
0.436 |
8.016 |
8.453 |
|
35 |
5.628 |
0.001 |
25.22 |
146.6 |
2276 |
2423 |
146.6 |
2418 |
2565 |
0.505 |
7.847 |
8.353 |
|
40 |
7.384 |
0.001 |
19.52 |
167.5 |
2262 |
2430 |
167.5 |
2406 |
2574 |
0.572 |
7.684 |
8.257 |
|
45 |
9.593 |
0.001 |
15.26 |
188.4 |
2248 |
2436 |
188.4 |
2394 |
2583 |
0.638 |
7.526 |
8.164 |
|
50 |
12.34 |
0.001 |
12.03 |
209.3 |
2234 |
2443 |
209.3 |
2382 |
2595 |
0.703 |
7.372 |
8.076 |
VAPORI SURRISCALDATI
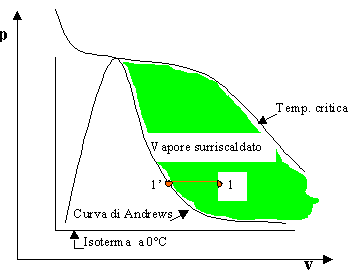
Si trovano nella regione compresa tra l’isoterma critica e a destra della curva di Andrews . I vapori saturi vengono anche chiamati gas reali .Tale zona è ancora caratterizzata dal fatto di non avere a disposizione equazioni di stato e in più il vapore surriscaldato non è più in equilibrio con il liquido: avremo ancora bisogna di tabelle.
Ci sono due modi per trattare tale stato: uno generale e uno particolare.
Noi non procederemo con quello particolare che si basa sulla teoria dei gas reali, ma adotteremo un metodo generale che permette di estendere i risultati dei vapori saturi a quelli surriscaldati.
Supponiamo di volere conoscere le proprietà termodinamiche del punto 1 della figura soprastante.
Nota la pressione p1 e la temperatura T1 troviamo p1' = p1, in quanto è una trasformazione a pressione costante per costruzione, e T1( p1' ) dalle tabelle dei vapori saturi. Note tali coordinate l’entalpia specifica sarà così definita:
![]()
Il calore specifico che compare lo trovo tabulato sulle tabelle dei vapori surriscaldati, che a differenza di prima, sono tabelle a doppia entrata:
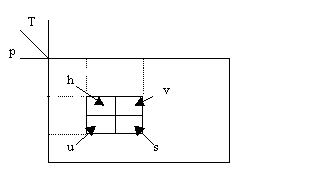
Per ogni coppia p,T posso avere o i valori delle 4 grandezze incognite, o, alternativamente, i valori di Cp e Cv a cui si ricorre per il calcolo delle altre coordinate come abbiamo visto nel caso dell’entalpia specifica.
In questo caso la ricerca per tentativi risulta essere più difficile in quanto la tabella è a doppia entrata e si rischiano di trovare false soluzioni se la tabella è molto grossolana.
Riporto qui di seguito un esempio di tabella relativa all’acqua e vapore surriscaldato:
|
Pressione di 1 bar |
Pressione di 2 bar |
|||||
|
Temperatura |
v |
h |
s |
v |
h |
s |
|
0 |
0.0010002 |
0.0 |
-0.0002 |
0.0010002 |
0.1 |
-0.0001 |
|
10 |
0.0010002 |
42.0 |
0.1510 |
0.0010002 |
44.1 |
0.1510 |
|
20 |
0.0010017 |
83.9 |
0.2963 |
0.0010017 |
64.0 |
0.2963 |
|
30 |
0.0010043 |
125.7 |
0.4365 |
0.0010043 |
125.8 |
0.4365 |
|
40 |
0.0010078 |
167.5 |
0.5721 |
0.0010078 |
167.5 |
0.5721 |
|
50 |
0.0010121 |
209.3 |
0.7035 |
0.0010121 |
209.3 |
0.7035 |