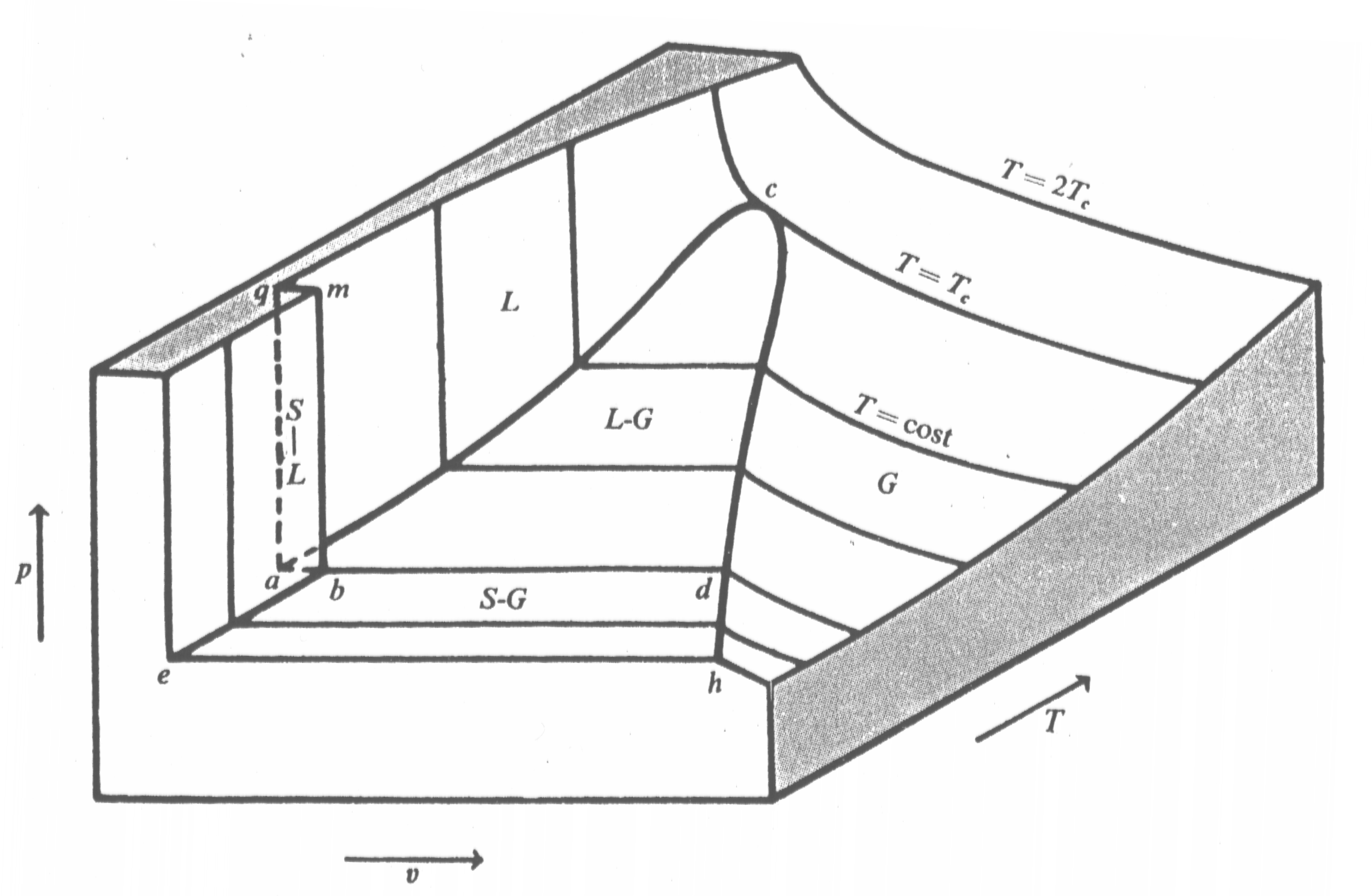
 Fig.1 - Superficie (p,v,T) per una sostanza che, solidificando, aumenta di volume.
Fig.1 - Superficie (p,v,T) per una sostanza che, solidificando, aumenta di volume.Sistemi chimicamente omogenei
In generale al variare delle tre variabili di stato avremo che sia l’aspetto esteriore che lo stato fisico della sostanza varierà. Se si definisce un sistema cartesiano in tre dimensioni, riportando sugli assi la pressione, il volume specifico e la temperatura, ad ogni punto del grafico corrisponde una terna di valori. Unendo tutti i punti ottenuti sperimentalmente per una sostanza pura, poiché sono sempre due le coordinate termodinamiche libere, si ottiene una superficie, detta (p,v,T), ad ogni punto della quale corrisponde un unico stato di equilibrio del sistema.
 Fig.1 - Superficie (p,v,T) per una sostanza che, solidificando, aumenta di volume.
Fig.1 - Superficie (p,v,T) per una sostanza che, solidificando, aumenta di volume.
Le regioni segnate con S,L,G sono caratterizzate dalla presenza di una sola fase, rispettivamente solida, liquida o gassosa; all’interno della campana coesistono due fasi. Al di sopra dell’isoterma critica (![]() ), ma non troppo lontano si ha la regione dei gas reali mentre per temperature maggiori e pressioni più basse la sostanza pura tende a comportarsi come un gas perfetto.
), ma non troppo lontano si ha la regione dei gas reali mentre per temperature maggiori e pressioni più basse la sostanza pura tende a comportarsi come un gas perfetto.
Per maggiore chiarezza e facilità di rappresentazione si usa solitamente un diagramma bidimensionale, ottenuto dalla proiezione del diagramma precedente sul piano (p,v); quella che si ottiene (vedi Fig.2) è una rappresentazione univoca della superficie (p,v,T).
La linea ac descrive gli stati fisici dove possono coesistere liquido e vapore in cui è presente solo la fase di vapore ed è definita curva limite inferiore; la curva cd descrive gli stati fisici in cui possono coesistere liquido e vapore in cui c’è solo vapore ed è definita curva limite superiore. Il punto in cui le due curve si incontrano è detto punto critico; in questo punto l’isoterma critica presenta un flesso orizzontale. Al di sotto delle curve limite vi è la regione del vapore saturo dove la fase liquida e di vapore coesistono contemporaneamente. A destra della curva limite superiore vi è la regione del vapore surriscaldato. Le curve isoterme per ![]() hanno due discontinuità dove incontrano le curve limite poiché nella zona dei vapori saturi le trasformazioni isoterme avvengono a pressioni costanti.
hanno due discontinuità dove incontrano le curve limite poiché nella zona dei vapori saturi le trasformazioni isoterme avvengono a pressioni costanti.
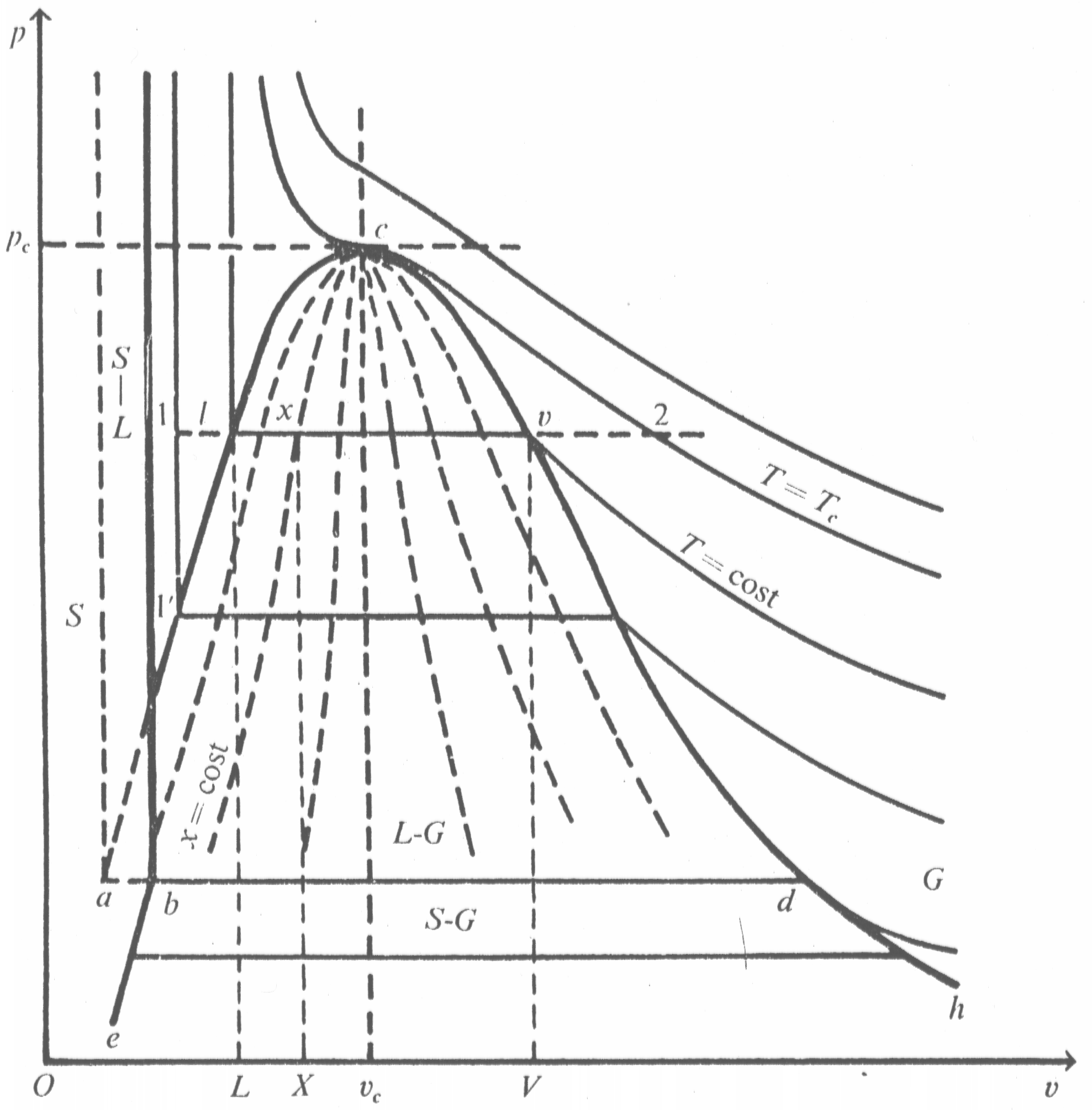
Fig. 2 – Diagramma termodinamico (p,v) di una sostanza che solidificando aumenta di volume
E’ da notare che la temperatura resta costante durante il passaggio di fase solo per processi quasi-statici e quindi molto lenti. Questo è un diagramma degli stati di equilibrio e da informazioni solo sugli stati estremi all’equilibrio di una trasformazione; dunque non serve a descrivere l’intero processo di trasformazione, che , nel caso di trasformazioni molto rapide, non passa attraverso stati di equilibrio.
I diagrammi o le tabelle riportano dati sperimentali e quindi danno informazioni che sono rispettate nel caso reale mentre per le formule analitiche esiste sempre un certo margine d’errore.
Equazione di stato
Poiché le variabili libere sono due si può supporre che esista un legame analitico che dia la terza variabile in funzione delle altre due, così come per i gas perfetti esisteva la relazione PV=MRT oppure pv=RT; per ogni terna (p,v,T) esiste uno stato fisico corrispondente. Va osservato che all’interno delle curve limite, nella zona dei vapori saturi, due variabili sono bloccate ovvero p e T degenerano in un’unica coordinata termodinamica, per cui l’equazione di stato coincide con la tabella.
Nella regione dello stato solido e dello stato liquido il volume è quasi costante, tuttavia a causa della dilatazione termica si avrà in generale l’equazione di stato data da:
![]()
![]() (1)
(1)
dove ![]() è il coefficiente di dilatazione termica, dipendente dalla sostanza considerata. Questo coefficiente è importante nello scambio termico convettivo di un liquido: considerando un recipiente contenente del liquido e posto su un fuoco si osserva che il liquido al centro, dove vi è temperatura maggiore, si dilata e quindi sale in superficie dove si raffredda e di conseguenza ridiscende lungo le pareti; questo moto è per l’appunto detto convettivo e permette il trasporto di calore in un liquido.
è il coefficiente di dilatazione termica, dipendente dalla sostanza considerata. Questo coefficiente è importante nello scambio termico convettivo di un liquido: considerando un recipiente contenente del liquido e posto su un fuoco si osserva che il liquido al centro, dove vi è temperatura maggiore, si dilata e quindi sale in superficie dove si raffredda e di conseguenza ridiscende lungo le pareti; questo moto è per l’appunto detto convettivo e permette il trasporto di calore in un liquido.
Nella zona dei vapori surriscaldati e dei gas reali si ha un’equazione di stato simile a quella dei gas perfetti ma modificata da un fattore numerico z che varia per ciascun punto del diagramma; si ha così l’equazione di stato
![]() (2)
(2)
dove z è detto fattore di compressibilità, è un numero puro e varia per sostanze diverse.
Ci interessa , a questo punto, calcolare le proprietà termodinamiche (energia interna, entalpia, entropia) della sostanza nei vari stati. Poiché queste grandezze sono riferite a meno di una costante additiva è possibile assegnare valore nullo a uno stato di riferimento, che in questo caso è il punto triplo indicato nel diagramma (p,v) con a.
![]() L’energia interna di un liquido nel punto si può calcolare lungo qualsiasi trasformazione reversibile; noi scegliamo la curva limite inferiore:
L’energia interna di un liquido nel punto si può calcolare lungo qualsiasi trasformazione reversibile; noi scegliamo la curva limite inferiore:
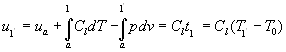 (3)
(3)
dove ![]() è il calore specifico costante lungo la curva limite inferiore (per l’acqua
è il calore specifico costante lungo la curva limite inferiore (per l’acqua ![]() = 4,187 KJ/Kg k). In generale il secondo integrale non è trascurabile ma nella pratica per un liquido si commette un errore molto piccolo trascurandolo.
= 4,187 KJ/Kg k). In generale il secondo integrale non è trascurabile ma nella pratica per un liquido si commette un errore molto piccolo trascurandolo.
Procedendo in modo analogo per trovare l’entalpia si ottiene:
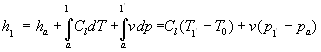 (4)
(4)
Per l’acqua il secondo termine è numericamente trascurabile rispetto al primo tuttavia questa approssimazione non vale per tutte le sostanze. Da quanto detto si ottiene che, ove valgono le approssimazioni fatte, l’energia interna e l’entalpia sono uguali nello stato liquido.
Dalla relazione ![]() otteniamo l’espressione per l’entropia:
otteniamo l’espressione per l’entropia:
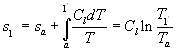 (5)
(5)
Si può procedere ora a un confronto con le espressioni delle medesime grandezze per un gas perfetto. Per un gas perfetto che operi una trasformazione a volume costante vale l’equazione ![]() e quindi:
e quindi:
![]() (6)
(6)
Per l’entalpia di un gas perfetto si usa una trasformazione a pressione costante e così dall’equazione ![]() si ricava:
si ricava:
![]() (7)
(7)
Per trovare l’entropia ci si può servire dell’equazione ![]() o di
o di ![]() e della equazione
e della equazione ![]() , ottenendo:
, ottenendo:
![]() (8)
(8)
![]() (9)
(9)
Tenendo conto della relazione, data dall’equazione dei gas perfetti,![]() si ottiene infine:
si ottiene infine:
![]() (10)
(10)
![]() (11)
(11)
Un terzo modo per calcolare l’entropia si ottiene tramite l’equazione dei gas perfetti e alla relazione ![]() :
:
![]() (12)
(12)
Dunque per un liquido, rispetto a un gas perfetto, si ha, per quel che concerne l’energia interna e l’entalpia, ![]() ,mentre per quel che riguarda l’entropia si trascura il termine
,mentre per quel che riguarda l’entropia si trascura il termine ![]() o
o ![]() .
.
Le proprietà del vapore sulla curva limite superiore non sono facilmente analizzabili analiticamente per cui si usano le tabelle. Le difficoltà principali si hanno nella zona del vapore saturo, quando sono presenti vapore e liquido; è necessario determinare per il punto che si vuole esaminare il titolo, che è dato dal rapporto tra la massa alla fase di vapore e la massa totale, secondo la relazione:
![]() (13)
(13)
Risulta evidente che sulla curva limite inferiore ![]() e sulla curva limite superiore
e sulla curva limite superiore ![]() . Per un punto x sul segmento a pressione costante congiungente l e v della figura 2 l’entalpia sarà data dall’espressione:
. Per un punto x sul segmento a pressione costante congiungente l e v della figura 2 l’entalpia sarà data dall’espressione:
![]() (14)
(14)
dove ![]() ,ovvero la differenza tra l’entalpia dello stato liquido e quella dello stato vapore a pressione costante è uguale a una grandezza indicata con r e detta calore latente di vaporizzazione. Tale grandezza è uguale al calore necessario per passare da l a v, infatti
,ovvero la differenza tra l’entalpia dello stato liquido e quella dello stato vapore a pressione costante è uguale a una grandezza indicata con r e detta calore latente di vaporizzazione. Tale grandezza è uguale al calore necessario per passare da l a v, infatti ![]() poiché la trasformazione è a pressione costante. Analogamente si ottengono per il punto in esame:
poiché la trasformazione è a pressione costante. Analogamente si ottengono per il punto in esame:
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
dove ![]() ,
,![]() ,
,![]() sono dette energia interna specifica differenziale, entropia specifica differenziale e volume specifico differenziale; si possono trovare i loro valori alle varie pressioni e per le varie sostanze nelle tabelle.
sono dette energia interna specifica differenziale, entropia specifica differenziale e volume specifico differenziale; si possono trovare i loro valori alle varie pressioni e per le varie sostanze nelle tabelle.
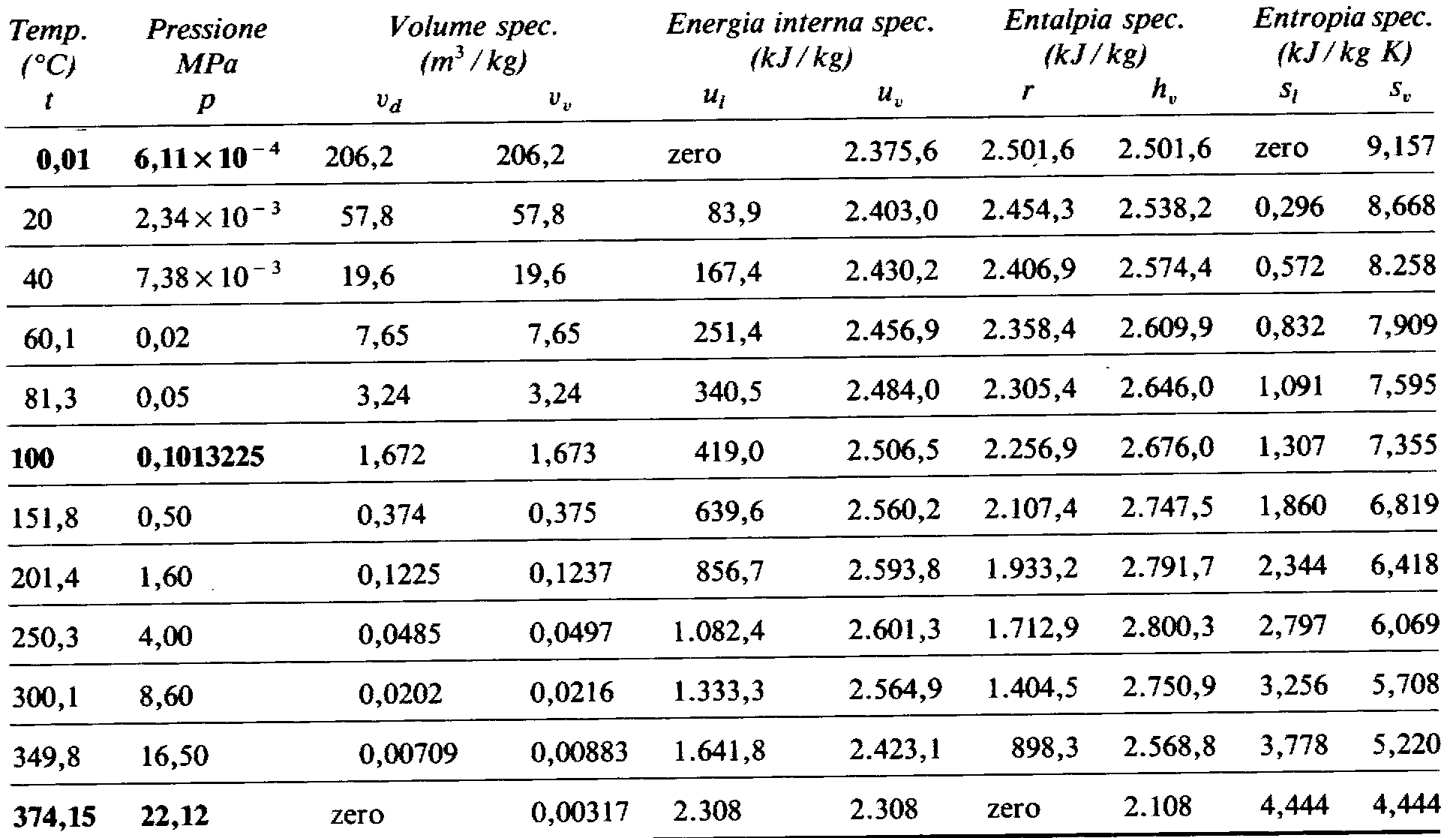
Fig.3 Caratteristiche di stato e termiche del vapore d’acqua saturo (dal punto triplo al punto critico)