PROPAGAZIONE ESTERNA
INDICE
1. SOMMA DI LIVELLI
Ipotizziamo di avere due sorgenti L1 e L2
![]()
Trattandosi di sorgenti incoerenti si sommano le loro intensità. Si ottiene:
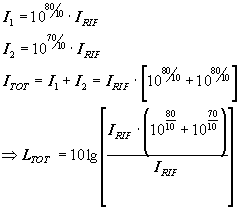
Sommando a un livello di 80 dB un altro che è 10 dB più basso, l'incremento ottenuto è inferiore a mezzo decibel. Si può costruire un diagramma dell'incremento di livello in funzione della differenza dei livelli, come si può notare nella figura 1.
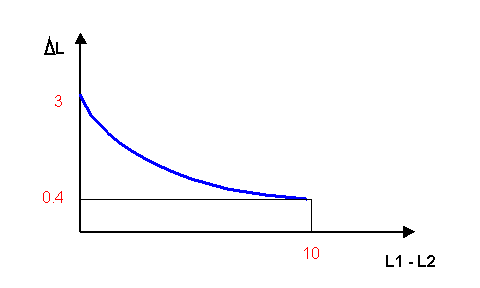
Figura 1 - Incremento di livelli -
Nella pratica quindi se un livello è inferiore ad un altro di 10 dB, diventa trascurabile.
2. DIFFERENZA DI LIVELLI
Ipotizziamo di dover misurare il rumore prodotto da una macchina. Da una prima misurazione con la macchina in funzione si rilevano 84 dB, disattivando la macchina e andando a rilevare il rumore dell'ambiente si ottengono 77 dB. Pertanto per ottenere il rumore effettivo della macchina si deve sottrarre il rumore dell'ambiente.
Si definisce:
L1 = rumore macchina più ambiente
L0 = rumore ambiente
L11 = rumore della macchina ripulito del rumore di fondo.
Non essendo i segnali correlati si sottraggono le intensità.
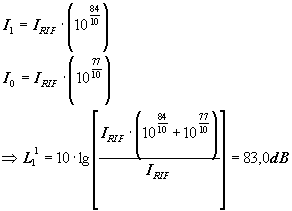
3. LIVELLO DI POTENZA (LW)
Il livello di potenza viene usato per quantificare, in decibel, quanto una sorgente emette; infatti ci possono essere sorgenti molto potenti che danno luogo a livelli bassi poiché lontane o schermate, viceversa sorgenti molto meno potenti che danno luogo a livelli alti poiché molto vicini al condotto uditivo, come ad esempio le cuffie di uno stereo. Occorre quindi separare l'emissione dalla propagazione.
Il livello di potenza non è un livello sonoro ma un livello energetico.
![]()
Dove P = Potenza
Po = Potenza di riferimento = 10 exp-12 w
4. LEGAMI TRA LIVELLO DI INTENSITA' E LIVELLO DI POTENZA
Si possono distinguere tre differenti legami tra livello d'intensità e di potenza a seconda del tipo di sorgente.
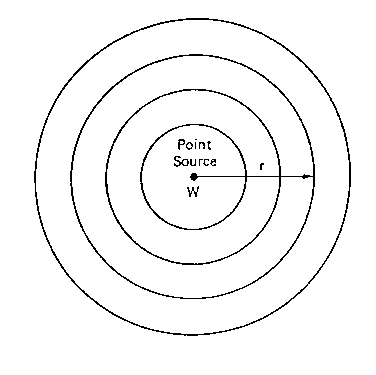
Figura 2 - Sorgente puntiforme -
Il valore d'intensità in una sorgente puntiforme è definito dalla formula 2.
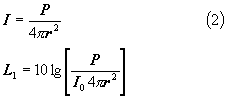
Moltiplicando e dividendo per P0 e S0
Dove: P0 = potenza presa come riferimento = 10 exp-12 w
I0 = intensità presa come riferimento = 10 exp-12 w/m2
S0 = area presa come riferimento = 1m2
Si ottiene (formula 3):
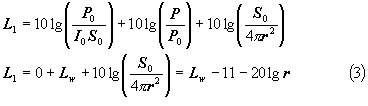
Si ha quindi una attenuazione di 6 dB per raddoppio di distanza.
E' possibile fare un diagramma del livello di intensità in funzione della distanza (fig. 3).
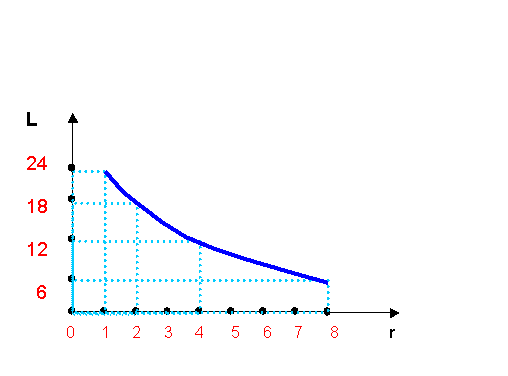
Figura 3 - Livelli d'intensità in relazione alla distanza -
La figura 4 mostra la propagazione del suono da una sorgente puntiforme.
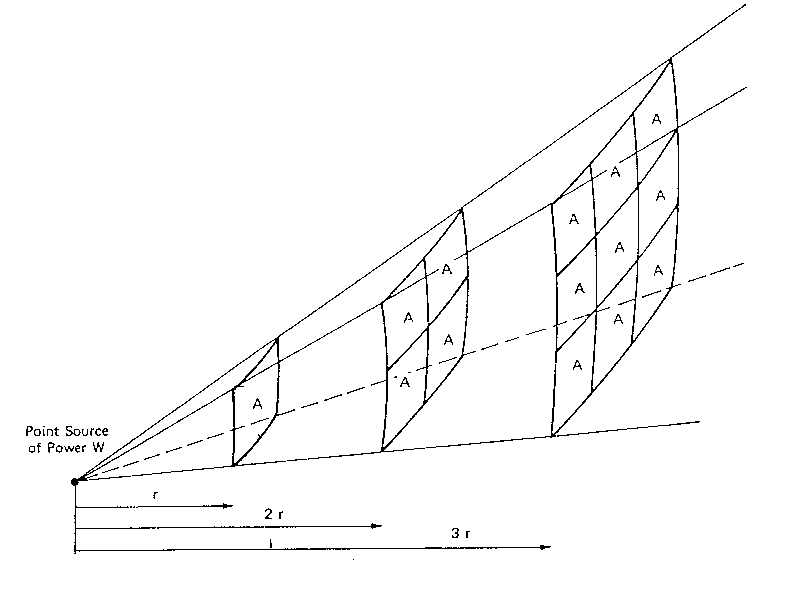
Figura 4 - Propagazione del suono da una sorgente puntiforme -
In questo caso il valore d'intensità è definito dalla formula 4:


Dove L= lunghezza tratto considerato.
Moltiplicando e dividendo per P0 e per S0 si ottiene:
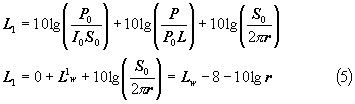
Dove L1W è il livello di potenza su metro.
Quindi per la propagazione in campo cilindrico si ha una attenuazione di 3 dB per ogni raddoppio di distanza.
La figura 5 mostra l'attenuazione del suono in sorgenti lineari.

Figura 5 - Propagazione del suono da una sorgente lineare -
La figura 6 mostra schematicamente la dispersione del suono in alcuni tipi di sorgenti puntiformi e lineari.
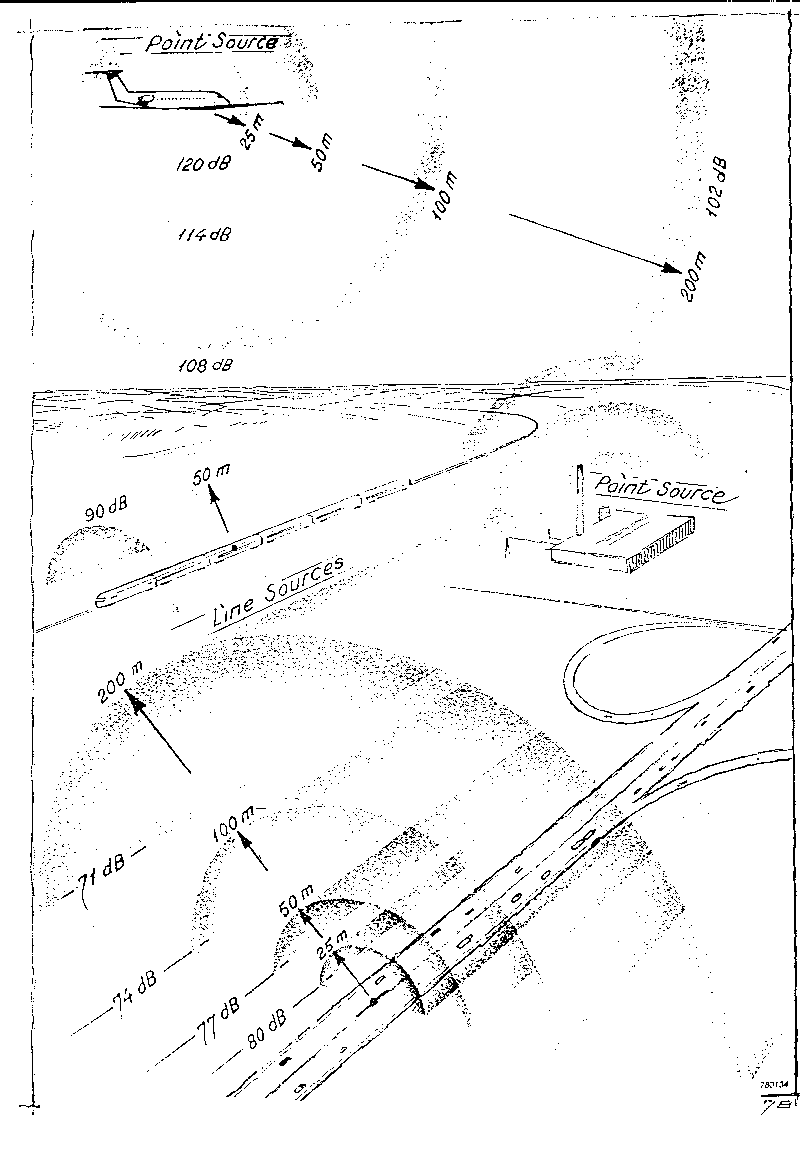
Figura 6 - Esempi di sorgenti lineari e puntiformi -
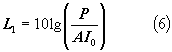
A = area della superficie considerata
Moltiplicando e dividendo per P0 e per So
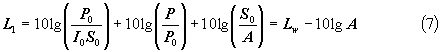
Non si ha più la divergenza geometrica e quindi il livello di intensità è costante.
5. ESEMPIO 1
- Misurazione del livello di intensità sonora di un edificio -
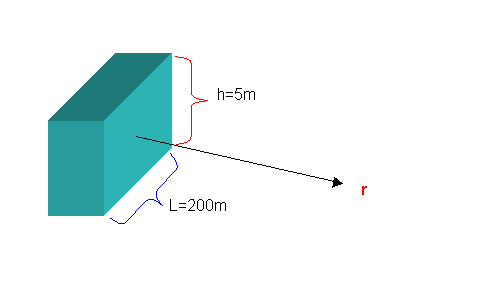
Figura 7
Allontanandosi ortogonalmente dall'edificio con lo strumento di misura ed osservando la variazione del livello sonoro si ottiene il seguente diagramma:
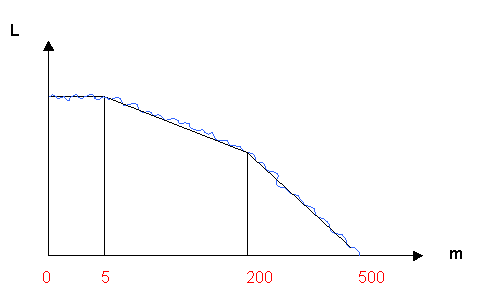
Figura 8 - Variazione di livello in funzione della distanza -
(0 - 5m) il livello sonoro è pressoché costante (lastra piana)
(5m - 200m) il livello sonoro cala di 3dB per raddoppio di distanza (sorgente lineare)
(200m -500m) il livello sonoro cala di 6 dB per raddoppio di distanza. (sorgente puntiforme)
6. ATTENUAZIONE IN ECCESSO
Le attenuazioni in eccesso sono effetti che si vanno a sottrarre al livello di intensità sonora dovuti alla propagazione atmosferica. La valutazione numerica è però difficile poiché dipendono dal tipo di terreno, dagli ostacoli, dalla temperatura variabile dell'aria e da altri fattori. Il livello sonoro effettivo è dato da:
Leffettivo = L1 - Aecc
Dove Aecc = attenuazione in eccesso
7. EFFETTO DELLA VELOCITA' DEL VENTO
Se un raggio sonoro passa da una zona senza vento ad una zona con vento, la velocità del suono si somma alla velocità del medesimo, come risulta in figura 9.
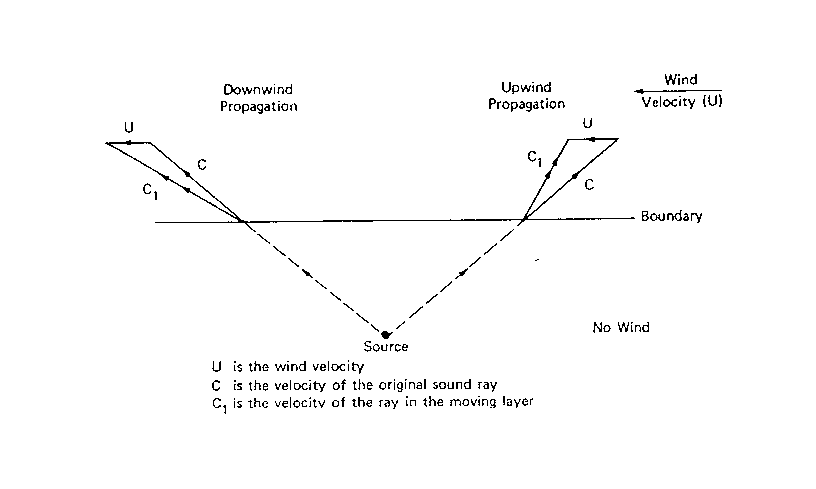
Figura 9 - Propagazione del suono in funzione del vento -
Se invece la velocità del vento varia linearmente con la quota, i raggi sonori curvano sottovento, come in figura 10.
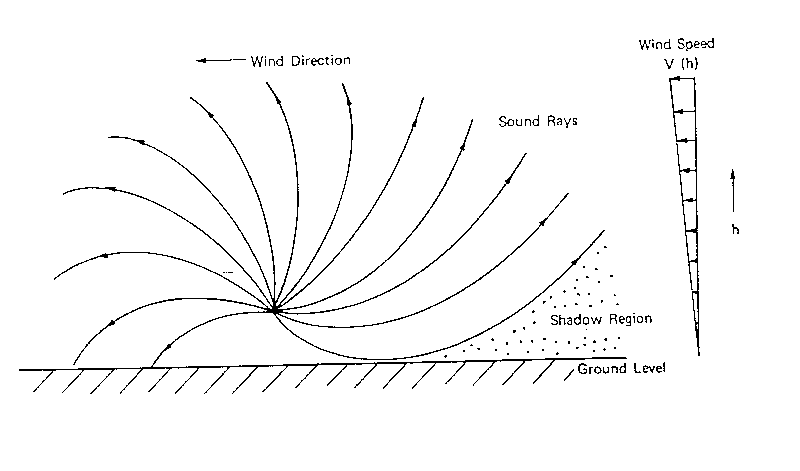
Figura 10 - Propagazione del suono in relazione al vento -
Questa curvatura fa si che si possono creare delle zone d'ombra (al di sotto dell'ultimo raggio tangente con il suolo), cioè delle zone dove il livello sonoro cala bruscamente.
8. PROFILO DI TEMPERATURA
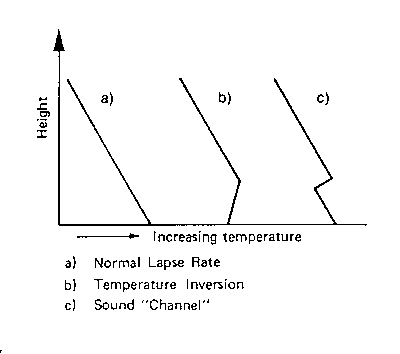
Figura 11 - Profilo di temperatura -
La temperatura normalmente cala all'aumentare dell'altezza (caso a).
Si possono avere però delle situazioni, in prossimità della terra, nella quale si ha la cosiddetta inversione termica, cioè la temperatura cresce all'aumentare dell'altezza (caso b).
Inoltre si può avere un altro caso nel quale la temperatura inizialmente va scendendo; in un secondo tempo, con il variare della quota, si ha l'inversione termica; successivamente la temperatura riprende a scendere.
Caso a -
La curvatura dei raggi tende normalmente verso le temperature fredde, come nel grafico rappresentato nella figura 12.a. Si possono così creare delle zone d'ombra.
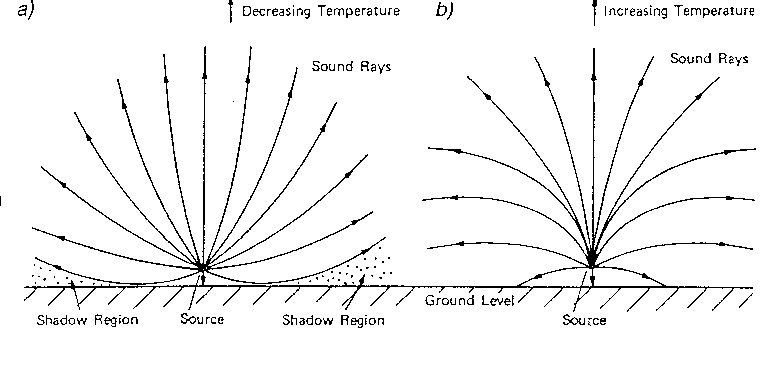
Figura 12 - Propagazione del suono in funzione della temperatura -
Caso b -
Con l'inversione termica non si creano più zone d'ombra quindi il rumore può oltrepassare eventuali ostacoli. Questo inconveniente è da tenere presente nel progetto di barriere per l'insonorizzazione delle autostrade.
Caso c -
Si crea un specie di canale d'aria e il suono rimane confinato all'interno dello stesso e può essere trasportato per parecchi chilometri con un'attenuazione molto bassa.
Esistono delle normative (ISO 9613) che descrivono le formule di calcolo per tenere presente questi effetti.
9. RIFLESSIONE DI UNA SUPERFICIE PIANA
Il problema della riflessione di una superficie piana viene risolto con la tecnica della "sorgente immagine", che prevede la disposizione di una sorgente virtuale in posizione speculare al piano riflettente rispetto alla sorgente (figura 13 ).
Questa approssimazione migliora tanto più la superficie è liscia e dura.
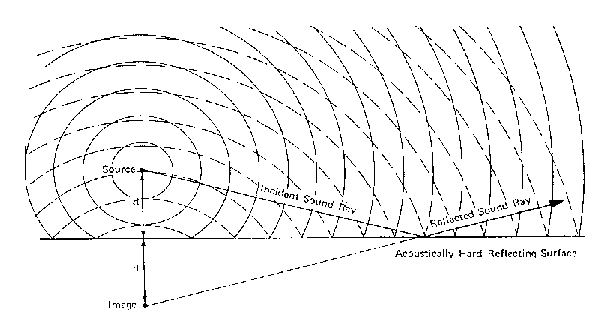
Figura 13 - Riflessione su una superficie piana -
Sommando il campo sonoro della sorgente, con quello della sorgente immagine si possono ottenere vari risultati a seconda della natura del suono.
In questo caso entrambe le sorgenti emettono lo stesso suono, che percorrendo cammini di diversa lunghezza, generano il fenomeno dell'interferenza.
Nei punti in cui i due segnali arrivano in fase (nel diagramma sono i punti nei quali si ha l'incrocio delle linee) si ha un incremento di 6 dB per raddoppio di distanza.
In realtà questo incremento sarà minore a causa del fatto che il livello sonoro della sorgente riflessa è leggermente inferiore (l'ampiezza infatti è proporzionale alla distanza e la superficie non è quasi mai riflettente al 100%). Nel centro delle figure delimitate dagli incroci delle circonferenze il suono arriva sfasato di 180° e si ha un cancellazione sonora. Anche qui, poiché il suono riflesso è minore del suono diretto, la cancellazione sarà solo parziale.
I calcoli per determinare il livello sonoro dipendono dalla fase e quindi basta spostare di pochi centimetri il microfono per avere risultati differenti.
Il suono emesso dalla sorgente riflessa, dovendo percorrere un distanza maggiore sarà assolutamente diverso e non correlato rispetto a quello della sorgente diretta; si sommano quindi le intensità.
L'incremento massimo sarà sempre minore o uguale a 3 dB ogni raddoppio di distanza. In questo caso è semplice calcolare L1 che risulta:
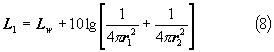
La formula 8 non considera però l'assorbimento del terreno. Normalmente quando si ha una certa intensità sonora incidente su un piano una quota di questa viene riflessa e una assorbita.
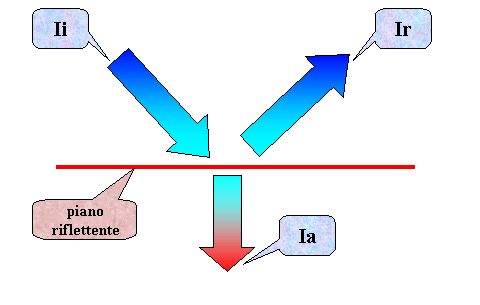
Figura 14 - Raggio incidente -
.
Si definisce il coefficiente di assorbimento a e il coefficiente di riflessione b : :

![]()
Per il principio di conservazione dell'energia, l'intensità incidente è uguale all'intensità riflessa più quella assorbita, quindi
a + r = i
allora L1 risulta:
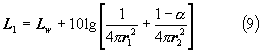
10. ASSORBIMENTO DELL'ARIA
L'aria non è un mezzo perfettamente elastico e provoca delle attenuazioni che dipendono:
L'attenuazione non dipende invece dalla temperatura. L'assorbimento è massimo quando l'aria è secca e a frequenze molto elevate. Vedi figura 15
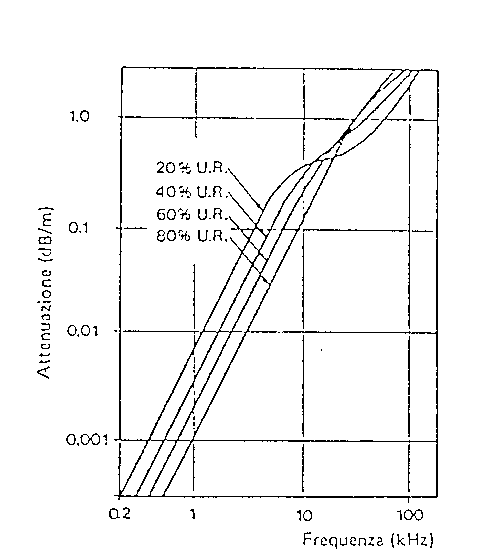
Figura 15 - Attenuazione dell'aria -
11. DIFRAZIONE O SCHERMATURA
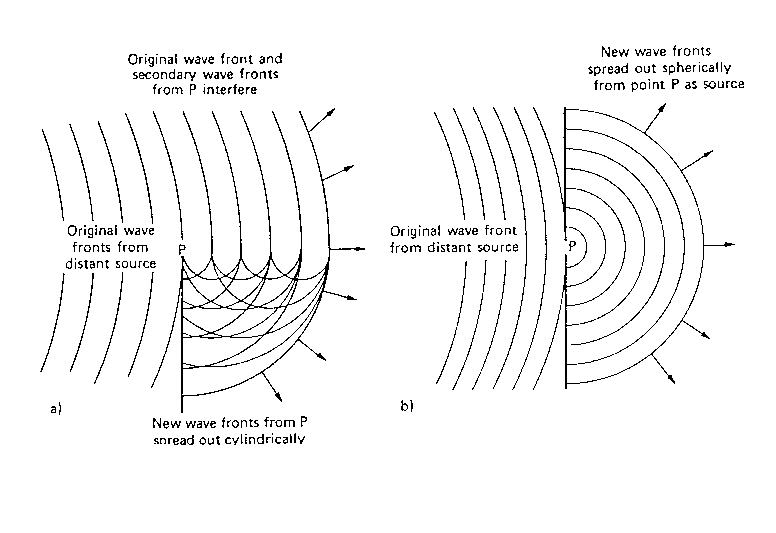
Figura 16 - Effetto di uno schermo (a) e di un buco (b) sulla propagazione del suono alle basse frequenze -
La figura 16 mostra quello che avviene alle basse frequenze attraverso un muro di cinta (figura 16.a) e attraverso un buco in una parete (figura 16.b). Il buco o lo schermo diffrangono le onde che arrivano, formando dei fronti d'onda curvi, che sembrano essere prodotti dal bordo di difrazione stesso. Questo fenomeno è legato alla natura ondosa della propagazione acustica e fa si che non si crei un'onda vera propria dietro allo schermo.

Figura 17 - Effetto di uno schermo (a) e di un buco (b) sulla propagazione del suono alle alte frequenze -
Alle alte frequenze si può notare un miglioramento come da figura 17. C'è infatti una parziale ricomposizione dell'onda nella zona successiva allo schermo.
In generale è però difficile da quantificare.
C'è un caso molto semplice nel quale è stata trovata una soluzione analitica semplificata:
è la formulazione di MAEKAWA, che vale nel caso di schermi sottili di lunghezza indefinita e sorgenti puntiformi.
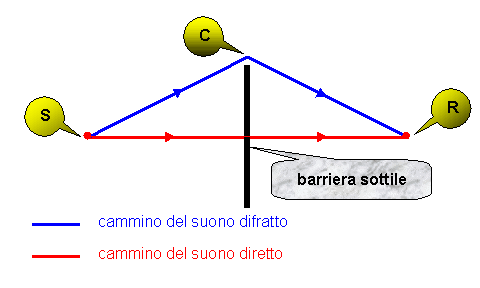
Figura 18 - Differenza di cammino a causa di una barriera sottile -
Allora la variazione di cammino risulta:
D L = LDIRETTO - LDIFRATTO = 10lg (3 + 20N) (10)
dove N è il numero di FRESNEL
![]()
l è la lunghezza d'onda e d è definito da:
![]()
D L varia linearmente in funzione di N come si può vedere in figura 19.
Con questa formula è possibile calcolare l'altezza di barriere insonorizzanti come nel caso di schermi per autostrade.

Figura 19 - Diagramma di Maekawa -
12. TEOREMA DI FOURIER
Un qualsiasi segnale complesso può essere descritto tramite la sommatoria di un numero infinito di sinusoidi. In acustica si usa considerare P(t ) inteso come forma d'onda di pressione, poiché i segnali che provengono dai microfoni sono generalmente segnali di pressione.
![]()
13. TRASFORMATA DISCRETA DI FOURIER
Nella pratica non si possono considerare un numero infinito di sinusoidi ma bisogna fare una opportuna discretizzazione su:
Il segnale viene così "discretizzato 3 volte", introducendo varie approssimazioni.
La trasformata discreta permette di passare da un segnale nel tempo al rispettivo spettro. Lo spettro è un grafico che porta in ordinata il valore dei livelli e in ascissa le frequenze discretizzate. Se il suono è puro si ha una sola ampiezza ad un'unica frequenza.
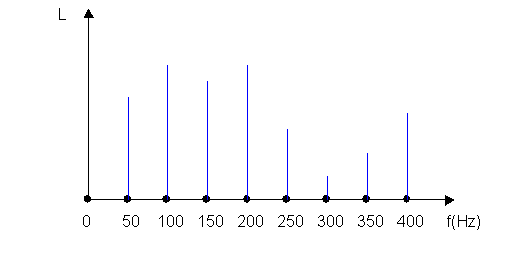
Figura 20 - Spettro di un segnale -
Sul grafico di figura non viene riportata la fase. Tuttavia la fase assoluta non ha alcun significato fisico; può diventare un dato rilevante invece quando si hanno più segnali, come ad esempio nel caso di strumenti di misura dotati di più canali.
Il livello totale può essere calcolato come somma energetica dei livelli delle singole bande.
![]()
Nel campo delle frequenze, per ricostruire un segnale, si sommano le varie rese spettrali; per giustificare questa somma energetica al posto della somma in modulo fase è necessario risalire al significato fisico della trasformata di Fourier.
Ciascuna riga spettrale è una componente sinusoidale con frequenza propria.
Vedi figura 21.

Figura 21 - Componenti sinusoidali -
In questo modo le armoniche non interferisco tra loro quindi è come se fossero tante sorgenti diverse.
La rappresentazione in frequenza è tanto più dettagliata quanto più è lungo il tempo di analisi del segnale.