Università degli Studi di Parma

Corso di Laurea in Ingegneria Elettronica, Informatica, delle Telecomunicazioni

Anno accademico 1998/99

Corso di Fisica Tecnica

Docente: Prof. Angelo Farina

Autore: Lorenzo Rosa (lrosa@ieee.org)

Matricola: 88448

Lezione del 5/10/98

Ore: 8:30-10:30

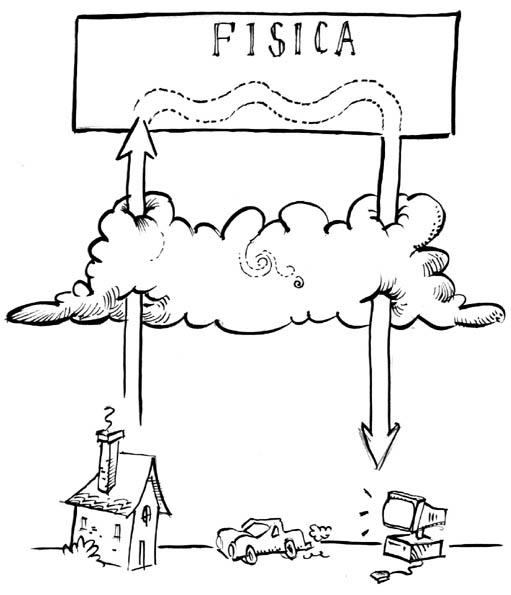
Quando si parla di fisica bisogna affrontare un problema basilare: passare dal mondo reale all’aspetto matematico. Nel mondo reale esiste un terreno, ed esiste una moltitudine di oggetti su di esso: case, automobili, computers. Questi oggetti tecnologici vengono progettati e verificati dagli ingegneri, mentre la loro costruzione è solitamente affidata ai tecnici. Al di sopra del mondo reale c'è il mondo della fisica.

Diversamente dal mondo reale, nel mondo della fisica non esistono case, automobili, computers, ma concetti astratti, che sono le grandezze fisiche (temperatura, tempo, lunghezza, ...). Tra le grandezze fisiche si costituiscono dei legami scrivendo delle espressioni matematiche, che possono derivare da principi fisici o da leggi fisiche, oppure essere delle espressioni empiriche.

I principi fisici sono leggi superiori che sono credute vere in quanto tali, perché discendono direttamente dal credere che esista il mondo reale. Quest'approccio è il fondamento della fisica e non è banale come sembra, se è vero che ancora alla vigilia dell’Illuminismo un filosofo del calibro di Spinoza negava l’esistenza del mondo reale.

Le leggi fisiche sono leggi naturali che approssimano i fenomeni che avvengono nel mondo reale. I risultati ottenuti sono perciò approssimati e non hanno lo stesso livello di verità di quelli dei principi fisici, e sono validi solo se si verificano determinate ipotesi.

Le espressioni empiriche hanno un livello di verità ancora più basso ed un ambito di validità ristretto, essendo sottoposte ad ipotesi più restrittive. Tuttavia forniscono un risultato numericamente valido nel loro ambito e spesso hanno il vantaggio di essere delle espressioni più semplici.

La nuvola rappresenta la barriera concettuale che esiste tra il mondo reale ed il mondo della fisica. Il compito dell’ingegnere è quello di superare questa barriera ed essere in grado di passare dal mondo reale a quello della fisica e viceversa.

Oltre a questo metodo esiste la possibilità di soluzione diretta: anziché passare per un processo di astrazione si risolve direttamente nel mondo reale, senza uso di equazioni e strumenti di calcolo. La soluzione vera è sempre quella diretta, se è possibile determinarla, perché è esente dalle approssimazioni introdotte dalla modellazione, che comunque non può dare un risultato diverso. In caso ci siano discrepanze, non è lecito attribuirle a fantomatici "errori di misura", è il modello matematico che presenta delle imprecisioni.

Per costruire i modelli nel mondo della fisica si utilizzano espressioni semplici, costituite da somme, moltiplicazioni, equazioni ordinarie. Esiste tuttavia un livello di astrazione più elevato che utilizza espressioni molto complicate, ma molto potenti, che sono le equazioni differenziali. Ciò comporta il superamento di un’ulteriore barriera concettuale per approdare al mondo della matematica.

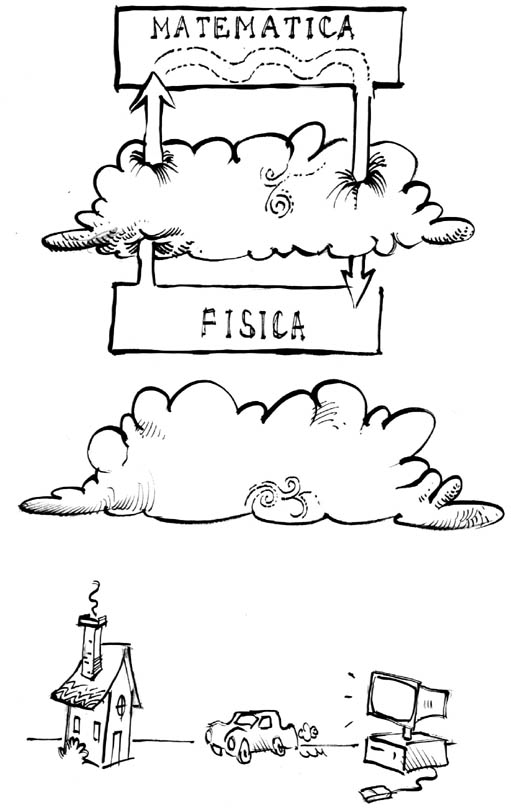
Quest'approccio, dovuto a Newton, fu oggetto di controversie tra lui e Leibniz, che sosteneva l’inesistenza dell’infinitamente piccolo, che è un concetto fondamentale per il calcolo infinitesimale. E’ stato invece dimostrato che si tratta di un approccio molto potente e di grande utilità per la risoluzione dei problemi fisici, ma che non è alla portata di tutti gli ingegneri a causa dell’elevato livello di astrazione. Infatti l’ingegnere ha a che fare con problemi strettamente legati alla realtà, per cui è necessario restare con i piedi per terra e questo rende difficili passaggi troppo astratti; tuttavia bisogna rendersi conto che esiste anche questa possibilità e cercare di sfruttarla.

In ogni caso il metodo più redditizio resta sempre quello di trovare una soluzione partendo dal reale e darla direttamente in termini reali senza utilizzare modelli.

Una grandezza fisica, come la lunghezza, la massa, il tempo, è un’entità che si può esprimere numericamente, cioé digitizzare, mediante un procedimento chiamato misura.

L’operazione di misura ha come risultato la scrittura di un’equazione algebrica in cui una grandezza fisica è uguagliata ad un numero moltiplicato per un’unità di misura opportunamente definita. Ad esempio, per la lunghezza si può scrivere:

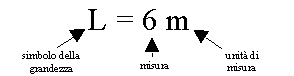
In questo processo è importante l’aspetto dell’omologia: non ha senso confrontare tra di loro grandezze che hanno natura diversa, la misura di una grandezza esprime quante volte nella grandezza da misurare è contenuta l’unità di misura omologa.

L’omologia si verifica considerando la dimensione della grandezza, cioé scrivendo un’espressione tra parentesi quadre nella quale compaiono le grandezze fondamentali del sistema utilizzato. Per la lunghezza l’espressione è:

Il sistema di unità di misura obbligatorio per legge in Europa è il Sistema Internazionale (SI), nel quale esistono sette grandezze fondamentali:

Le dimensioni fisiche di una qualsiasi grandezza esprimono tra parentesi il prodotto dei simboli delle grandezze fondamentali con i rispettivi esponenti per dare coerenza dimensionale. Ad esempio:

Nel SI esistono anche grandezze non fondamentali, dette grandezze derivate (dicitura impropria, perché in realtà sono le unità di misura ad essere derivate), determinate a partire dalle grandezze fondamentali con l’ausilio di opportune leggi fisiche, la cui scelta è convenzionale e dipende dal sistema di unità di misura utilizzato.

Se il sistema è coerente (come è il SI), la derivazione è fatta usando solo moduli unitari delle grandezze fondamentali (senza introdurre fattori di proporzionalità) e ciò che si ottiene è un modulo unitario della grandezza derivata.

Ad esempio, per derivare la forza nel SI si utilizza la prima legge di Newton:

(1)

in cui a sua volta

(2)

L’unità di misura della forza nel SI è il newton (N), tale che

(3)

e la formula dimensionale è

(4)

Saper scrivere questa espressione è importante per fare la verifica dimensionale di un’equazione, vale a dire controllare che tutti i termini dell’equazione siano omogenei dal punto di vista dimensionale. Questa è una condizione necessaria per la validità di un’equazione, dal momento che una somma di grandezze di natura diversa non ha significato. Ad esempio, in un’equazione del tipo

(5)

si può notare che l’argomento del logaritmo deve essere per forza un numero puro (non ha senso fare il logaritmo di una grandezza fisica, e ciò in generale anche per tutte le altre funzioni trascendenti): ciò comporta che i termini D e D₀ debbano essere dimensionalmente omogenei, in modo che il rapporto sia un numero puro.

Tuttavia esistono equazioni vere che in apparenza non sono dimensionalmente omogenee, come

(6)

in cui j è un’entalpia specifica (cioé per unità di massa), t è una temperatura e x è un numero puro. Questo accade perché in realtà l’equazione vera è un’altra, cioé

(7)

in cui c_p ha valore unitario e rappresenta un’entalpia specifica per kelvin.

La verifica dimensionale non garantisce che l’equazione sia corretta, ma in termini probabilistici elimina gran parte degli errori.

Oltre ad essere obbligatorio, l’utilizzo del SI è disciplinato dalla legge e da una serie di norme che fissano convenzioni e regole operative che è molto importante rispettare: durante la stesura di un progetto, la legge impone di produrre e conservare un’adeguata documentazione tecnica, che poi può essere acquisita agli atti in caso di controversia giudiziaria; è automaticamente illegale presentare un documento che non contenga le unità di misura del SI, o in cui ad esempio non sia indicata correttamente l’unità di misura del risultato.

Vi sono diversi organismi normativi a seconda dell’ambito di competenza: in ambito nazionale italiano le regole ingegneristiche sono disciplinate dalle norme UNI, in ambito europeo dalle norme CEN, ed in ambito mondiale dalle norme ISO. In caso di mancanza di normativa da parte di uno di questi organismi, fa testo la norma emessa da quello immediatamente superiore.

In particolare l’utilizzo del SI è regolato in Italia dalla norma CNR-UNI 10003 (disponibile nella Biblioteca di Facoltà), di cui possiamo riassumere alcune caratteristiche:

1) Le unità di misura devono essere indicate senza essere seguite dal puntino.

2) A volte è opportuno a fini pratici utilizzare multipli o sottomultipli delle unità di misura: la norma ammette solo multipli e sottomultipli ad intervalli di 10³. A questi corrispondono dei prefissi:

Ciò comporta che multipli e sottomultipli come dam, dm, cm, hg e quintale siano fuorilegge, mentre non lo è la tonnellata, in quanto corrisponde a 10³ kg. L’unica eccezione a questa regola è il BAR, unità di misura della pressione tale che

(8)

dove in realtà l’unità di misura del SI è il pascal (Pa), definito come

(9)

L’eccezione è ammessa per l’utilità pratica del BAR, il cui modulo unitario corrisponde alla pressione atmosferica.

3) Multipli e sottomultipli devono essere usati in modo che il numero contenga solo cifre significative:

• la scrittura 300 Mm indica un risultato noto con una precisione di 1 Mm
• la scrittura 300000 km indica un risultato noto con una precisione di 1 km
• la scrittura 300000000 m indica un risultato noto con una precisione di 1 m

Perciò è importante che la precisione (numero di cifre significative) rispetti l’accuratezza (numero di cifre a cui è attribuito un effettivo significato fisico) del risultato. La differenza è evidente se si considera, ad esempio, la rosata di pallini prodotta da un colpo di fucile: un’elevata precisione indicherebbe che la rosata è molto concentrata attorno al baricentro, mentre un’elevata accuratezza indicherebbe che il baricentro della rosata cade molto vicino al bersaglio. Per quanto sia preciso, un fucile poco accurato difficilmente colpisce il bersaglio.

Raramente un calcolo ingegneristico ha un’accuratezza dell’1% o migliore, molto più spesso essa si attesta su valori intorno al 5% o peggiori: è importante eseguire i calcoli intermedi con la massima precisione disponibile, ma poi bisogna evitare di presentare un risultato con troppe cifre significative e limitarsi a quelle che rispettano l’accuratezza dichiarata.

Per specificare correttamente l’accuratezza è molto utile la notazione scientifica, perché può essere usata con un qualsivoglia esponente intero, anche non multiplo di 3: una scrittura come 300 Mm si può anche scrivere con diversa precisione come 300·10⁶ m, o 3000·10⁵ m, oppure 30·10⁷ m, a seconda dell’accuratezza con cui il risultato è noto.

4) Quando esiste, si deve usare il nome dell’unità derivata al posto della sua rappresentazione in termini di unità fondamentali, per cui, ad esempio, l’unità di misura della forza, il newton, si indica con N, e non con kg·m/s².

5) Un caso particolare riguarda l’unità di misura del lavoro (J) e quella della potenza (W), in quanto spesso sono troppo piccole per diversi casi pratici: al loro posto il SI suggerisce di utilizzare nella presentazione del risultato i multipli per 10³, cioé kJ e kW, anche se i calcoli vanno comunque eseguiti con i moduli unitari delle grandezze.