Per trattare le onde sferiche è necessario ricavare l’equazione di D’Alambert in coordinate sferiche.

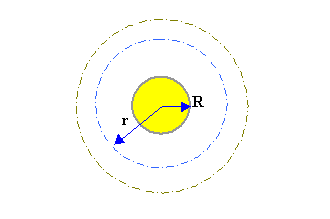
Prendiamo come sorgente del campo sonoro una sfera di raggio R, che pulsando, non ha raggio costante, ma variabile in funzione del tempo t secondo la relazione R(t) = R₀ + DR sin( wt ), dove R₀ indica il raggio della sfera a riposo.

 Viene definito il campo sonoro per i soli valori di r > R:

Fig. 1 – Sfera pulsante del campo sonoro.

Per ottenere l’equazione di D’Alambert in coordinate sferiche ci occorre considerare il potenziale della velocità F(r,t) come funzione del tempo e della distanza dalla sfera, e il prodotto FR costante.

L’equazione e’ la seguente:

  (1)

Svolgendo la derivata otteniamo:

(2)

L’equazione ottenuta risulta essere irrisolvibile ,e’ conveniente pertanto operare la sostituzione Y = Fr nella (1) ottenendo:

(3)

 La soluzione dell’equazione differenziale è data da :

(4)

Osserviamo che il secondo termine dell’espressione rappresenta la parte di onde entranti nella sfera , quindi dato che e’ di interesse soltanto la parte del campo sonoro all’esterno , il suddetto termine può essere trascurato.

 Operando ora la sostituzione inversa F = Y / r , si ottiene:

(5)

 Perché l’equazione (5) abbia significato fisico è necessario trascurare il termine immaginario dato dall’esponenziale complesso, quindi la forma definitiva del potenziale della velocità acustica è data da :

  (6)

 Rimane ora da calcolare il valore di Y₊ imponendo le condizioni al contorno valide sulla pelle della sfera.

Vale che :

(7)

Essendo poi F il potenziale della velocita’ si ha:

(8)

uguagliando infine le due espressioni ottengo:

(9)

da cui si ricava:

(10)

La conoscenza di questo valore permette di definire l’espressione della velocita’ acustica per un generico r>R :

(11)

L’ampiezza del campo velocita’ e’ dato da due termini entrambi decrescenti e dipendenti dal prodotto Kr:

• Kr<1 : prevale il primo termine dell’espressione (11) che cala con il quadrato del raggio.
• Kr>1 : prevale il secondo termine che cala invece linearmente.

Nota l’espressione di f ricavata precedentemente:

(12)

si puo’ calcolare la pressione sonora del campo:

(13)

Osservo che l’andamento della P(r) si mantiene lineare con il raggio a qualsiasi distanza ; nella stessa sorgente pertanto p e u non hanno piu’ la stessa ampiezza , non sono piu’ cioe’ accoppiate.

 Si ha poi che l’impedenza acustica:

(14)

e’ complessa .Si introduce quindi uno sfasamento tra p e u ed un modulo di z non piu’ costante ma variabile con r. Una variazione di r pertanto mi comporta sia una variazione del modulo che della fase. Vengono in particolare sfasati tanto piu’ quanto ci si avvicina alla sorgente stessa.

 Ricaviamo il valore di z nei due casi limite:

 - campo lontano : Kr>>1

(15)

In questo caso p e u sono in fase , l’impedenza risulta la medesima dell’onda piana progressiva.

 - campo vicino : Kr<1

(16)

L’impedenza risulta puramente immaginaria: sfasamento di p/2 a breve distanza dalla superficie vibrante che comporta un trasporto di energia nullo.Il termine al denominatore non puo’ essere pertanto trascurabile.

OSS: Essendo K=w/c si ha che a basse frequenze anche il valore di K e’ basso , per cui ci vuole un elevato R per potere entrare nel campo lontano. Il ragionamento e’ analogo per le alte frequenze.

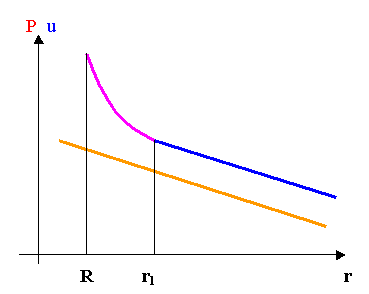
Fig.2-pressione/velocita in funz. del raggio.

 Se la sorgente e’ piccola , risulta difficile farle irradiare energia , bisogna pertanto calcolare l’intensita’ sonora :

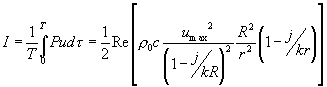  (17)

Quando siamo in condizioni di campo lontano (Kr>>1) vale:

(18)

dove P indica la potenza irradiata , che vale quindi:

(19)

In condizioni di campo vicino vale invece la seguente:

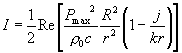(20)

dove Pmax risulta essere:

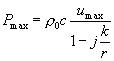
(21)

Si osservi che in questo caso l’intensita’ sonora diminuisce per r tendente a 0 , e cosi’ anche la potenza. Si ha pertanto una diversa energia in gioco , a seconda che ci si trovi vicino o lontano dalla sorgente:

• vicino : ho piu’ potenza reattiva che attiva . Nel misurare l’intensita’ della sorgente , nel caso fossi troppo vicino alla sorgente , commetterei un grave errore di misura.
• lontano : riesco ad avere anche solo potenza attiva.

La sonorita’ mi indica il numero di raddoppi della sensazione sonora.

Supponendo di avere un suono A con una pressione sonora Prms(A)=1 Pa , se volessi un suono il doppio piu’ forte di A , dovrei avere una Prms(B)=3,16 Pa .

Definendo con S(A) e S(B) le sonorita’ di A e B ho che :

Se volessi poi che un terzo suono abbia S(C)=3 dovrebbe avere :

c=Prms(c)=3,16²=10 Pa

Si definisce il livello sonoro come segue:

(22)

dove I₀ indica la piu’ debole intensita’ del suono che un uomo possa percepire. Osserviamo che il livello sonoro cosi’ definito e’ sempre positivo.

 L’intensita’ sonora puo’ essere scritta anche cosi’:

(23)

dove :

(24)

(25)

E’ quindi lecito scrivere l’espressione del livello sonoro come segue:

(26)

valida pero’ solamente per un’onda piana progressiva.

Per quanto riguarda le altre si ha che il livello di u segue il livello di p , per cui le frequenze alle quali si ha il massimo di u e p non coincidono. Che i suoni siano in fase o no la densita’ non la considero , posso pertanto in ogni punto sommare energia cinetica e potenziale , per cui vale sempre il concetto D=cost con l’intensita’. In ogni punto dello spazio avro’ quindi un vettore intensita’ che sara’ la somma vettoriale dei due vettori sorgente , e tale che:

Si osservi che ad un raddoppio di intensita’ corrisponde un aumento di 3 dB, mentre ad un raddoppio di p oppure u ne corrisponde uno di 6 dB.

Esempio:

Si considerino ora due sorgenti ad una distanza r da un punto , in cui si vuole fare la misurazione. Viene calcolato il valore del livello sonoro nei due casi:

• segnali diversi :

• segnali uguali :