Università degli Studi di Parma
Corso di Laurea in Ingegneria Elettronica, Informatica,
delle Telecomunicazioni
Anno accademico 1998/99
Corso di Fisica Tecnica
Docente: Prof. Angelo Farina
Autore: Rocco Petrolini
Matricola: 110418
Lezione del 15/12/98
Ore: 8:30-10:30
Irraggiamento - Applicazioni
I CORPI GRIGI
Proprietà
Coefficiente di assorbimento
La gran parte dei modelli che si studiano non sono neri, ne esiste tuttavia una categoria che può essere studiata con relazioni simili a quelle dei corpi neri: i corpi grigi.
Un corpo si dice così se il suo coefficiente di assorbimento
a,
che normalmente è![]() ,
è invece costante:
,
è invece costante:
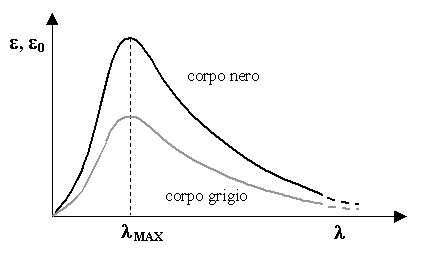 |
Fig. 1 - Spettri di emissione (alla stessa temperatura).
Se rappresentiamo (fig. 1) le due emissioni (poteri emissivi specifici)
di un corpo nero (e 0) e di uno grigio
(e ) alla stessa temperatura di colore (stesso ![]() max),
possiamo osservare che ad ogni lunghezza d'onda il corpo grigio emette
sempre una frazione costante di quella del corpo nero. Supponiamo un corpo
grigio con coefficiente a=0.8: ha sempre un potere emissivo specifico
che è 0.8 volte quella del corpo nero.
max),
possiamo osservare che ad ogni lunghezza d'onda il corpo grigio emette
sempre una frazione costante di quella del corpo nero. Supponiamo un corpo
grigio con coefficiente a=0.8: ha sempre un potere emissivo specifico
che è 0.8 volte quella del corpo nero.
Estensione della legge di Stefan-Boltzmann al corpo grigio
Osserviamo per prima cosa che indicando con q0 ilpotere emissivo integrale del corpo nero, quello del corpo grigio,
![]() , (1)
, (1)
non dipende dalla temperatura: infatti pur variando la forma dello spettro ad ogni T, per ogni lunghezza d'onda rimarrà costante il rapporto e/e0.
Utilizzando l'espressione data da Stefan-Boltzmann per il corpo nero e sostituendola nella (1) a q0 si ottiene:
![]() (2)
(2)
E' la stessa formula del corpo nero a meno del coefficiente a (noto per ogni corpo grigio).
Dobbiamo fare attenzione alla presenza di a<1 nell'analisi
dello scambio termico. Data una radiazione incidente qinc
la frazione (1-a)qinc verrà riflessa e
solo la quantità aqinc verrà assorbita
(fig.2) (ricordiamo che un corpo nero avrebbe assorbito integralmente la
radiazione ricevuta).
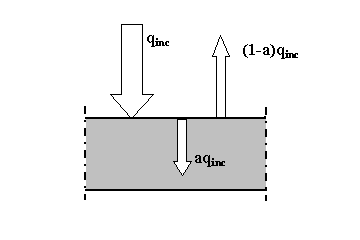 |
Fig. 2 - Scambio termico per un corpo grigio.
Per i corpi grigi si dovrà sempre tenere conto della quota riflessa;
il fatto che a sia costante su tutto lo spettro, e indipendente
quindi dalla temperatura, ci semplificherà notevolmente i calcoli.
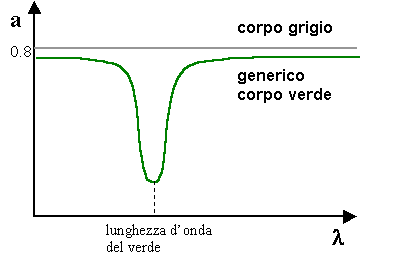 |
Fig. 3 - Spettri di assorbimento di un corpo grigio e di uno verde.
Un corpo monocromatico ha uno spettro di assorbimento con un unico "buco"
(fig.3) ma in generale se è di un colore non netto e definito avrà
un coefficiente di assorbimento a(l )
molto più variabile. In questi casi, se considero il valore del
potere emissivo integrale, potrò sempre scrivere che per il corpo
non grigio: q=aq0 intendendo per a un opportuno ![]() (media
sull'intero spettro), ma a questo punto tale coefficiente dipende dalla
temperatura. Infatti dato che lo spettro di emissione del corpo nero cambia
in funzione della temperatura secondo la legge di Planck, l'emissione e0
andrà o meno ad eccitare i picchi che può avere lo spettro
di assorbimento e quindi, ricordando la formula del potere emissivo integrale
del corpo non nero, si può scrivere:
(media
sull'intero spettro), ma a questo punto tale coefficiente dipende dalla
temperatura. Infatti dato che lo spettro di emissione del corpo nero cambia
in funzione della temperatura secondo la legge di Planck, l'emissione e0
andrà o meno ad eccitare i picchi che può avere lo spettro
di assorbimento e quindi, ricordando la formula del potere emissivo integrale
del corpo non nero, si può scrivere:
![]() (3)
(3)
e 0 , che fa da fattore
di peso in questa media, dipende da T (lo spettro di emissione cambia con
la temperatura) e di conseguenza i valori mediati![]() .
.
Colore dei corpi e "grigezza"
In generale non è detto che un corpo grigio in senso termico sia di colore grigio nel senso della percezione visiva e viceversa; non dobbiamo lasciarci ingannare perché di tutto il campo della radiazione elettromagnetica che ha effetti energetici per noi importanti dal punto di vista termico, la parte delle lunghezze d'onda visibili è estremamente piccola e quindi la quota di energia che porta è modesta rispetto al totale di energia di tutto lo spettro di radiazione.
Possiamo considerare con buona approssimazione come corpi grigi certi
oggetti con superficie scabra, rugosa, diffondenti e non riflettenti, ma
che magari percettivamente ci appaiono di tutt'altro colore. Infatti se
un materiale contiene numerosi elementi chimici diversi e quindi le bande
spettrali sono distribuite con una certa uniformità, lo spettro
complessivo di emissione su tutto il campo delle lunghezze d'onda avrà
degli scostamenti non troppo rilevanti da quello del corpo grigio. D'altra
parte una superficie di alluminio anodizzato ad esempio, argentea, quasi
bianca, sostanzialmente grigia visivamente, dal punto di vista termico
non è grigia affatto! L'emissione spaziale di una tale lastra sarebbe
assolutamente diversa da quella prevista dalla legge di Lambert per il
corpo nero ![]() che
il corpo grigio invece deve rispettare (fig.4).
che
il corpo grigio invece deve rispettare (fig.4).
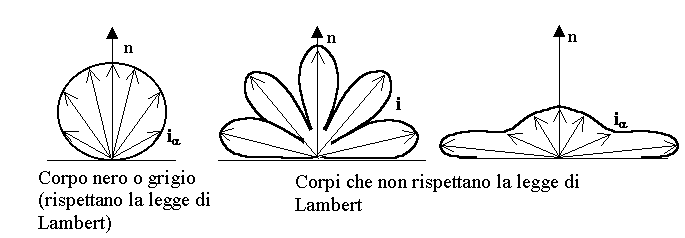 |
Fig. 4 - Solidi fotometrici.
Riassumendo, un materiale (corpo) si dice grigio, quando rispetta tutte
le leggi del corpo nero, con uno scostamento quantificabile da un unico
numero che è il coefficiente a costante per tutte le frequenze
e le direzioni dello spazio.
| NOTA
Proprietà ottiche dei corpi e colori: studi correlati e sintesi cromatica. Due scienze che si interessano di queste proprietà sono: l'illuminotecnica e la tecnica fotografica (rendering fotorealistico). Illuminotecnica: disciplina del campo della fisica tecnica che riguarda la progettazione degli impianti di illuminazione e quindi lo studio della radiazione luminosa sugli oggetti e negli ambienti. Le misure vengono fatte in lumen: W/m2 (si considerano solo i watt provenienti dalla luce visibile ponderati con una curva che corrisponde alla sensibilità dell'occhio umano). Tecnica fotografica (rendering fotorealistico) : al giorno d'oggi consiste nell'insieme delle discipline matematiche e geometriche che si occupano della creazione di immagini fotorealistiche e di realtà virtuale al computer, oltre che della fotografia di ambienti reali. Le superfici che entrano in gioco in questi studi vanno caratterizzate con una serie di parametri ottici e superficiali che non sono solo il coefficiente di assorbimento ma che ne descrivono l'aspetto cromatico, ad es. la tinta (hue) e il numero di colori base che la ricostruiscono sinteticamente (tricromia RGB, quadricromia CMYK). Nei monitor ad esempio attraverso i tre cannoni rosso, verde, blu e i valori numerici assegnati alle loro intensità si ricostruisce (quasi) qualsiasi grado di luminosità e di colore . Nei sistemi moderni si hanno 256 livelli di ciascuno dei tre colori base RGB (colore a 24bit). E' difficile comprendere come questo possa essere in accordo con lo schema usuale di rappresentazione dei colori dello spettro visibile (spettro dell'iride); ricordiamo che tale rappresentazione è monodimensionale data unicamente dalle lunghezze d'onda; in natura però esistono tinte che non sono monocromatiche ma sfumate, non corrispondenti ad alcun colore puro, risultato di un "mix" di colori diversi, visto che un corpo come abbiamo già visto, non ha in generale, un solo "buco" di assorbimento per una singola lunghezza d'onda, ma più di uno. L'unico modo matematico-fisico corretto sarebbe quello di conoscere a(l ) per tutto lo spettro visibile; dividendolo in 2048 bande spettrali si potrebbe ottenere una cromatografia completa. Ma al calcolatore, se per ogni punto dello schermo definissimo 2048 colori sottocomponenti , ciascuno dei quali con l'opportuna ampiezza del segnale, sarebbe necessario un quantitativo di memoria troppo grande per descrivere l'immagine! La scelta di 3 colori (rosso, verde, blu) per ricostruire tutto lo spettro interpolandoli, garantisce una buona approssimazione (dal punto di vista percettivo) ma senza richiedere una mole esagerata di dati.
Se rappresentiamo graficamente l'insieme delle tinte ricostruibili otteniamo un triangolo cromatico (vedi figura) dove i colori all'interno sono descritti da tre valori che sono le quantità di rosso, verde, blu, che li compongono (distanze dai vertici). L'area dei colori da noi percepibili è però più vasta, qui si nota l'approssimazione e l'imprecisione di questo processo, una semplice sintesi a tre colori non può riprodurle tutte. |
Riflettenza dei corpi grigi
I corpi grigi presentano esclusivamente riflessione diffusa.
In generale invece per un corpo qualsiasi il grado di riflessione speculare
è importante e va studiato.
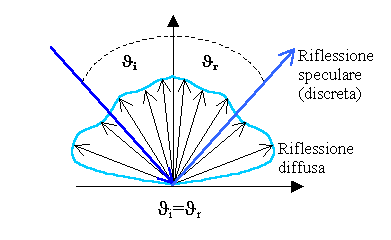 |
Fig. 5 - Un corpo che presenta riflessione diffusa e speculare.
Data una superficie con un certo grado di specularità e un raggio incidente (fig.5), dopo l'impatto si ha un'emissione diffusa (riflessione diffusa) secondo un certo solido fotometrico ma soprattutto anche una quota di emissione discreta (riflessione speculare) con una direzione ben precisa: l'angolo di incidenza J i è uguale all angolo di riflessione Jr.
Se poi il corpo è semitrasparente , si ha anche il fenomeno della
rifrazione
(fig.6).
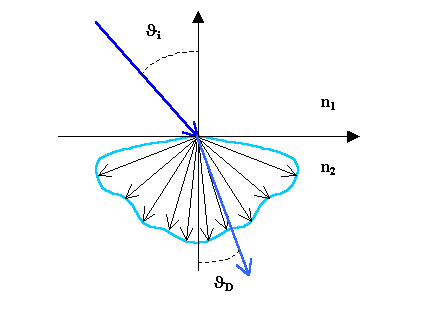 |
Fig. 6 - Rifrazione per un corpo semitrasparente (è stata omessa la riflessione).
L'energia che passa attraverso la superficie di separazione viene anch'essa suddivisa in altre due parti: una diffusa secondo un solido di emissione e l'altra discretizzata, che forma un angolo con la normale Jd diverso da J i dato dagli indici di rifrazione n1 e n2 dei due mezzi.
Non esistono corpi che presentano solo riflessione speculare, viceversa ne esistono altri che hanno solo la componente diffusa (essa non è mai trascurabile, nemmeno per uno specchio).
Nel campo dell'irraggiamento termico, la presenza della riflessione
speculare porta a calcoli complicati e si cerca sempre di trascurarla.
Nei modelli si considerano perciò solamente corpi grigi (solo riflessione
diffusa), ricordando però che è un'approssimazione, visto
che la maggior parte dei corpi reali non sono grigi e hanno una quota di
riflessione non diffusa spesso non trascurabile; si devono perciò
prevedere e accettare scostamenti anche notevoli fra i risultati teorici
e quelli reali sperimentali.
Corpi grigi e scambio termico per irraggiamento.
Irraggiamento tra superfici completamente affacciate.
Consideriamo due superfici grigie, diffondenti, infinite (si possono così trascurare gli effetti di bordo e semplificare i calcoli), separate da un mezzo perfettamente trasparente, completamente affacciate. Supponiamole a temperature diverse T1 e T2 con coefficienti di assorbimento a1 e a2.
Distinguiamo 3 casi in base ai valori dei coefficienti di assorbimento:
1) a1 = a2 =1 (entrambe le superfici
sono nere)
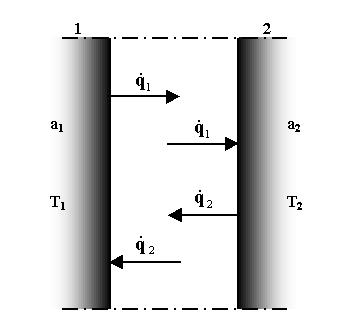 |
Fig. 7 - Scambio termico fra due corpi neri
La superficie 1 emette una quantità di calore ![]() (potere
emissivo integrale in W/m2) che viene interamente assorbita
dalla parete 2 (fig.7). Analogamente per la parete 2 (si ricordi che essa
emette una quantità q2 ¹q1
dato
che le temperature sono diverse).
(potere
emissivo integrale in W/m2) che viene interamente assorbita
dalla parete 2 (fig.7). Analogamente per la parete 2 (si ricordi che essa
emette una quantità q2 ¹q1
dato
che le temperature sono diverse).
Utilizzando la relazione di Prevost e applicando la legge di Stefan-Boltzmann visto che si tratta di corpi neri, otteniamo:
![]() (4)
(4)
2) a1=1, a2<1 (Una superficie
è nera e l'altra grigia)
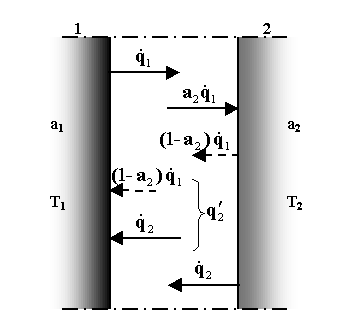 |
Fig. 8 - Scambio termico fra un corpo nero e uno grigio
Il corpo grigio 2, di tutto il calore ![]() emesso
da 1, assorbe solo
emesso
da 1, assorbe solo ![]()
e riflette ![]() che
torna sul corpo 1 assieme alla quantità
che
torna sul corpo 1 assieme alla quantità ![]() emessa
da 2 (fig.8).
emessa
da 2 (fig.8).
Quindi sul corpo 2 arriva complessivamente una quantità:
![]() (5)
(5)
che utilizzando il coefficiente di riflessione r diventa:
![]() (6)
(6)
Possiamo ancora applicare la relazione di Prevost ad es. per comodità sul corpo 1 (nero) e utilizzare s 0 e le T (Stefan-Boltzmann):
![]() (7)
(7)
perciò:
![]() (8)
(8)
3) a1<1, a2<1, a1¹a2(entrambe
le superfici sono grigie)
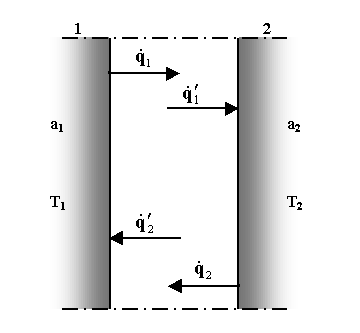 |
Fig. 9 - Scambio termico fra due corpi grigi.
Analogamente al caso precedente ,questa volta per entrambe le pareti (fig.9), possiamo scrivere:
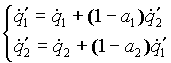 (9)
(9)
E' un sistema di due equazioni in due incognite; risolvendolo per sostituzione si ottiene:
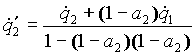 (10)
(10)
Scrivendo la relazione di Prevost per la superficie 1, sostituendovi la (10) e semplificando otteniamo:
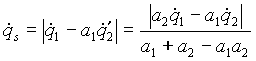 , (11)
, (11)
utilizzando poi s 0 e le temperature, diventa:
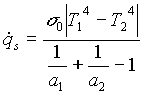 . (12)
. (12)
la (12) è la relazione che determina lo scambio termico tra due lastre piane parallele indefinite grigie.
Non importa la distanza, anche se comunque non deve esserci contatto, in modo da non avere scambio per conduzione.
E' da notare che se nell'intercapedine non' c'è il vuoto ma è presente un fluido, il calore si scambia sia per irraggiamento che per convezione. Si può allora immaginare che fra le lastre esistano due resistenze termiche:
una di convezione, lineare con la temperatura,
![]() (13)
(13)
e una di tipo radiante, non lineare,
![]() (14)
(14)
Più avanti si vedrà come si può linearizzare la (14) in modo da ottenerne una più semplice e comprensibile.
A basse temperature lo scambio radiante è sempre debole e prevale
quello convettivo; questo vale fino a temperatura ambiente, mentre sopra
gli 80°-100° il termine di irraggiamento non è più
trascurabile ed è dominante per temperature superiori a 300°-400°
.
| NOTA
Scambiatori per irraggiamento: i pannelli radianti. Utilizzati per riscaldare gli ambienti, si montano a soffitto delle stanze (anche se questa regola non viene sempre rispettata, compromettendo il funzionamento) e vi si fa scorrere acqua calda come nei termosifoni (che però sono scambiatori convettivi); lo scambio è soprattutto radiante a temperature anche vicine a quella ambiente per motivi costruttivi. Essendo montati a soffitto scaldano un cuscino di aria che rimane stazionaria (dovrebbe salire) e diventa un isolante perfetto che impedisce che il pannello scambi per convezione ma solo per irraggiamento. Scaldano le persone e il pavimento ma affatto l'aria (è trasparente e lascia passare integralmente la radiazione termica). Questa è una situazione molto salubre, visto che invece, respirare l'aria calda secca (proveniente dal riscaldamento a titolo costante di quella fredda esterna) generata dagli altri sistemi di riscaldamento (pompe di calore ecc.), causa problemi alle vie respiratorie. Lo svantaggio di questo sistema è che i pannelli hanno un basso coefficiente di scambio totale (hTOT @ 3w/m2k circa) e devono quindi essere di grandi dimensioni (in genere come tutta la stanza). |
Irraggiamento tra superfici parzialmente affacciate.
Consideriamo il caso di una cavità (stanza, camera di combustione
di un forno ecc.) che contiene un corpo, entrambi grigi (fig.10). Per semplificare
facciamo l'ipotesi che il corpo sia convesso (non può irraggiare
su se stesso) e la cavità sia concava.
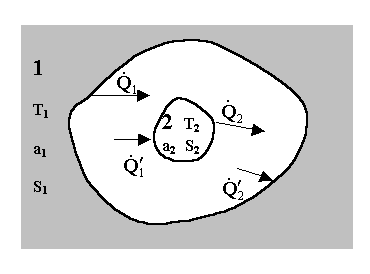 |
Fig. 10 - Irraggiamento tra superfici parzialmente affacciate.
Si conoscono T1 T2 , a1 a2 e le superfici dei due corpi S1 e S2.
Definiamo il Fattore di vista o fattore di forma:
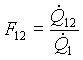 , (15)
, (15)
numero puro che esprime il rapporto fra la potenza che partendo dalla
superficie del corpo 1 va a colpire 2 e la potenza totale emessa da 1.
Ne esiste sempre il complementare e la somma di tutti i fattori di vista
tra superfici (fig.11) deve dare 1 (conservazione dell'energia).
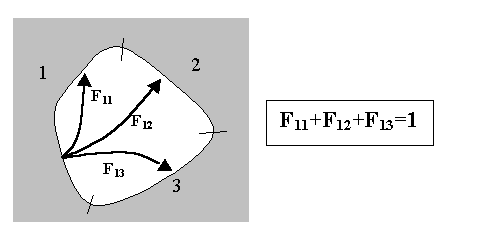 |
Fig. 11 -Fattori di vista per tre superfici affacciate.
Per i due corpi parzialmente affacciati visto che le superfici sono
diverse, non si può lavorare per unità di superficie quindi
al posto di ![]() nelle relazioni
si devono utilizzare le quantità complessive di calore e quindi
le potenze complessive
nelle relazioni
si devono utilizzare le quantità complessive di calore e quindi
le potenze complessive![]() . In fig.10,
come al solito con
. In fig.10,
come al solito con ![]() e
e ![]() si
indicano le emissioni proprie dei due corpi, mentre con
si
indicano le emissioni proprie dei due corpi, mentre con ![]() e
e ![]() le
quantità complessive che arrivano a colpire le superfici.
le
quantità complessive che arrivano a colpire le superfici.
Pertanto sarà:
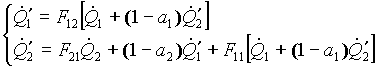 (16)
(16)
risolvendo il sistema per sostituzione, otteniamo:
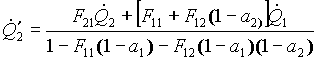 ; (17)
; (17)
ricordando che è F21=1 e F11=1-F12 e utilizzando la relazione di Prevost (per la potenza scambiata complessiva) si ha:
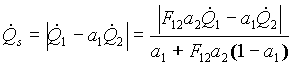 . (18)
. (18)
Dato che si ha poi:
![]() ,
, ![]() ,
(19)
,
(19)
la (18) equivale alla relazione:
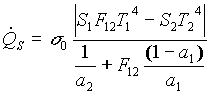 , (20)
, (20)
che nel caso di superfici completamente affacciate (F12=1
e S1= S2), considerando ![]() anziché
anziché ![]() ,
coincide con la (12).
,
coincide con la (12).
La (20) consente di determinare rapidamente il valore di F12; infatti se T1=T2, deve essere anche Qs=0, per cui dovendosi annullare il numeratore della (20) deve essere:
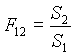 . (21)
. (21)
E' una relazione che vale solo se il corpo 2 è convesso (altrimenti emetterebbe in parte su di sé e i nostri calcoli precedenti non sarebbero più validi) e se entrambe le superfici sono isoterme.
Consideriamo un caso particolare: S1/S2 molto grande, cioè F12<<1. Nella (20) posso trascurare il 2° termine al denominatore; ricordando che possiamo scrivere S2=F12S1 si ottiene:
![]() . (22)
. (22)
Si osserva quindi che per un corpo dentro un ambiente grande (situazione frequente nei nostri problemi), entrambi grigi, si ottiene una relazione come se esso fosse contenuto in un corpo nero.
Linearizzazione del legame:
Per poter utilizzare l'analogia delle resistenze termiche equivalenti,
si vuole eliminare la dipendenza delle temperature dalle potenze quarte
nel termine radiante. Si vuole ottenere una funzione lineare, molto più
maneggevole e di immediata comprensione.
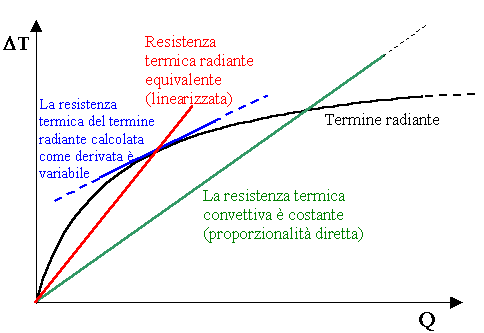 |
Fig. 12 - Resistenza termica equivalente per il termine radiante.
La resistenza termica è costante nel caso del termine convettivo in cui la relazione di proporzionalità è lineare (retta); per il termine radiante (dipendente dalle T4) si ha una sorta di parabola e la resistenza definita come tangente alla curva è variabile, con un'espressione troppo complessa e scomoda (fig.12).
Si vuole perciò trovare un circuito lineare equivalente che passi per gli stessi Q e D T: deve essere una secante alla nostra curva, passante per l'origine e per il punto in esame della curva del termine radiante: si ottiene così la resistenza equivalente. Non sarà costante ma dipenderà dal punto in cui sta operando il circuito e quindi dalle temperature in gioco. Del resto anche le resistenze convettive dipendevano da T, infatti:
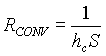 con hc = hc(T).
con hc = hc(T).
Similmente per lo scambio termico radiante si vuole ottenere:
![]() , (23)
, (23)
dove hr è il coefficiente di irraggiamento.
La linearizzazione consta nell'imporre:
![]() , (24)
, (24)
da cui otteniamo la formula per il calcolo di hr,:
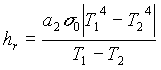 . (25)
. (25)
Dipende fortemente dalla temperatura, ma questo non è un problema,
dato che nei nostri problemi le temperature sono note, specialmente al
termine dei calcoli visto che in generale andremo a utilizzare questa formula
solo alla fine per presentare il termine radiante in forma lineare, per
mantenere l'analogia con le resistenze.
Esempio
Si vuole trovare una rete elettrica equivalente che fornisca la resistenza
termica complessiva per una parete di cemento e mattoni dotata di un intercapedine
di aria (fig.13):
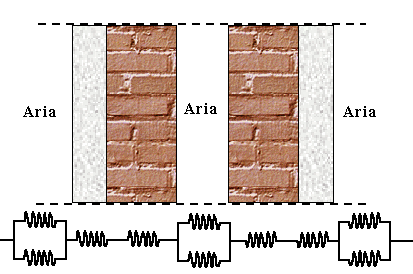 |
Fig. 13 - Rete elettrica equivalente per lo scambio termico complessivo.
Il cemento e i mattoni presentano resistenze termiche di conduzione in serie, mentre l'aria esterna e nell'intercapedine presenta due resistenze termiche di convezione e irraggiamento in parallelo.
La resistenza termica complessiva dell'aria si ottiene ricordando come si calcola quella elettrica nei casi di resistenze in parallelo nei circuiti:
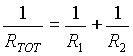 (25)
(25)
perciò se:
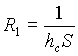 e
e 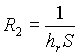 ,
(26)
,
(26)
si ottiene:
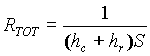 . (27)
. (27)
Risulta utile definire hTOT=hc+hr , che viene detto coefficiente di adduzione.