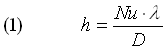
Contenuti:
Cenni di Teoria
Introduciamo in questa parte brevi cenni teorici sulla Convezione Naturale che ci serviranno per affrontare i successivi esercizi.
Come già introdotto nelle lezioni precedenti, la Convezione Naturale è un fenomeno che ha luogo ogni qualvolta un corpo viene posto in fluido che si trovi a temperatura diversa, in modo che si instauri uno scambio termico tra le due sostanze. Nelle prossimità della superficie del corpo, il flusso di calore determina una variazione della temperatura del fluido ed una conseguente variazione di densità. Le differenze di densità determinano il moto del fluido più pesante verso il basso e del più leggero verso l’alto. Quando il moto del fluido non è forzato da altre cause, come ventilatori e pompe, si ha pura convezione libera o naturale.
I problemi di scambio termico di tipo convettivo, molto spesso, si risolvono sostanzialmente calcolando il coefficiente di convezione. A tal fine si ricorre al numero di Nusselt sfruttando la relazione:
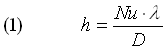
Il numero di Nusselt in generale dipende in generale dal numero di Grashof (Gr), numero di Prandtl (Pr), numero di Reynolds (Re), secondo una funzione generica f.
![]()
Nel caso specifico della convezione naturale, tuttavia, cade la dipendenza dal numero di Reynolds proprio perché il fluido non perturbato dallo scambio termico è in quiete.
![]()
Negli esercizi si usa una forma analitica approssimata della legge f indipendente da Re.
![]()
I parametri a, b, c dipendono dalla geometria del sistema e dal moto del fluido durante la convezione naturale stessa, che può essere laminare o turbolento.
Questa relazione ha origine sperimentale e di conseguenza fornisce un’approssimazione di Nu, e dunque del coefficiente di convezione. A questo punto è importante dire che l’errore con il quale le equazioni forniscono tale coefficiente non è inferiore al 20% in quanto la maggior parte dei dati sperimentali subisce scarti del ± 15% o più.
Tornando al discorso, i parametri a, b, c dipendono anche dal moto del fluido che può essere laminare o turbolento. In questo caso, tuttavia, il fluido ha velocità nulla non solo sulla superficie del corpo, ma anche a distanza infinita, ovvero il fluido non perturbato è in quiete. Ciò significa che non possiamo utilizzare il numero di Reynolds per stabilire il regime di moto; ecco allora che introduciamo, a tal fine, il numero di Rayleigh (Ra), definendolo in questo modo:
Numero di Rayleigh
![]()
Nella pratica, una volta calcolati i numeri di Pr e Gr, si calcola Ra, dopodiché si consulta una tabella che restituisce i parametri a, b, c in base al valore di Ra ed alla geometria del sistema. La tab. 1 ne fornisce un esempio. Sperimentalmente inoltre si è verifica il moto laminare solo per:![]() .
.
Tabella 1
- Formule sperimentali per il calcolo del numero di Nusselt: convezione naturale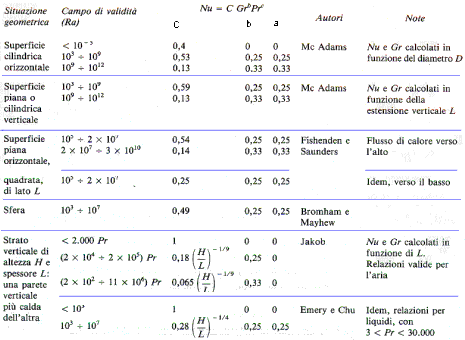
Precisiamo che sulla convezione naturale sono stati condotti studi sperimentali da diversi scienziati, con risultati differenti. Nella tab. 1, infatti, sono riportati anche i nomi dei rispettivi studiosi, per indicare che la validità dei dati è riferita proprio agli studi da loro effettuati.
Esercizio 1 - Convezione Naturale all’interno di un Condotto
Descrizione del Problema:
In fig. 1 è mostrato un condotto di sezione rettangolare, al cui interno c’è aria ferma. Il condotto è delimitato da 4 pareti: la parete superiore (1) è mantenuta a temperatura imposta di 0°C; le pareti laterali (2 e 3) sono anch’esse mantenuta a temperatura imposta di 100°C; la parete inferiore (4), invece, è adiabatica. Le misure del condotto sono riportate sotto la figura.
All’interno del condotto l’aria si porterà ad una temperatura media Ti: si chiede di determinare tale temperatura.
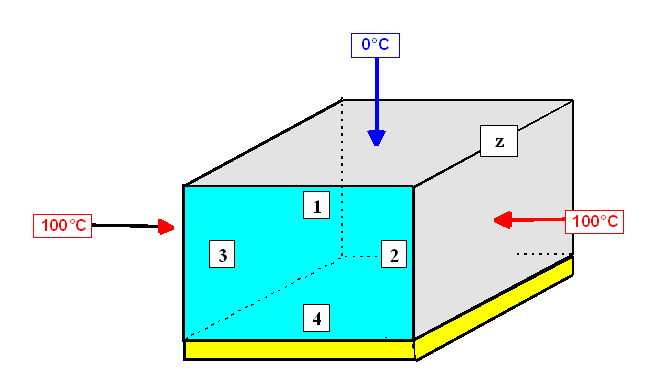
Figura 1
Dati del Problema:
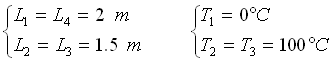
Soluzione:
Innanzitutto, facciamo alcune considerazioni sull’incognita Ti e descriviamo il fenomeno. Rappresentiamo il moto del fluido in sezione come in fig. 2. Possiamo senz’altro ipotizzare che l’aria, riscaldata dalla pareti laterali, salga fino alla parete superiore dove subisce un raffreddamento che la fa scendere attraverso un canale centrale. Sulla parete inferiore, invece, essendo questa adiabatica, abbiamo flusso imposto nullo: q=0.
Si viene quindi a stabilire un moto convettivo naturale costituito da una doppia rotazione che trascina anche il fluido più interno in una rotazione su se stesso. Tuttavia, solo la parte di fluido periferica viene a contatto con le pareti e ivi scambia calore attivamente, mentre si creano "noccioli" d’aria coinvolta fluidodinamicamente ma termicamente inerte.
In conclusione, è facile notare come l’aria non abbia una temperatura uniforme, ma distribuita puntualmente nella sezione in maniera complessa. Ciononostante, determiniamo Ti , come temperatura media a cui si porta idealmente il fluido.
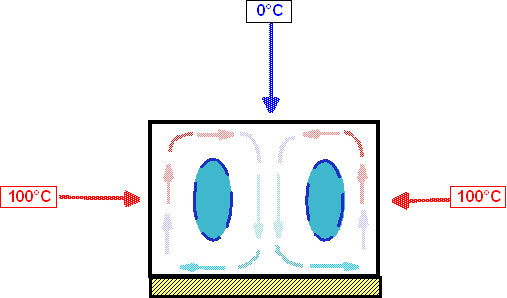
Figura 2
- Moto del fluido in una sezioneNel caso di un fluido che scorre dentro ad un condotto, del quale sia assegnato il profilo di velocità e si conosca pure la distribuzione di temperatura sulla sezione, si definisce una Temperatura di Bulbo, che rappresenta la temperatura media del fluido nella sezione. In questo caso è possibile calcolare la temperatura media con una relazione analoga al calcolo della velocità media:

Figura 3
- Esempio di profilo di velocità in un condotto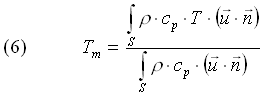
Purtroppo nel nostro caso il profilo di velocità non è assegnato, perciò non possiamo applicare la (6). Per risolvere il problema ricorriamo allora al circuito elettrico equivalente, pagando il prezzo della semplicità del modello con inevitabili approssimazioni.
Circuito Elettrico Equivalente
Avendo tre pareti che scambiano calore, introduciamo tre resistenze termiche, tutte dovute a scambi convettivi: R1 è dovuta allo scambio con la parete superiore, R2 e R3 allo scambio con le corrispondenti pareti laterali. Ai tre rami sono poi collegati i flussi orientati ![]() con ovvia corrispondenza.
con ovvia corrispondenza.
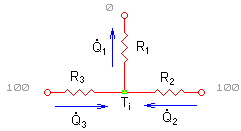
Figura 4
- Rete elettrica equivalenteRicordiamo inoltre che le resistenze termiche dovute a convezione sono esprimibili in questa forma:
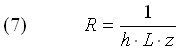
Dove h è al solito il coefficiente di convezione, mentre z rappresenta la lunghezza del tubo che non viene specificata nei dati del problema siccome non indispensabile per il calcolo di Ti.
Per semplificare il calcolo possiamo imporre arbitrariamente: z = 1 m.
Osserviamo che lo scambio termico presenta completa simmetria rispetto all’asse della parete 1; ciò significa che possiamo semplificare il problema ponendo:
![]()
Per risolvere la rete elettrica interpretiamo la Ti come la temperatura che, posta nel circuito elettrico equivalente, fa fluire sulle resistenze termiche i flussi che effettivamente fluiscono.
Scriviamo dunque il sistema di equazioni di ramo e sfruttiamo il principio di Kirchoff al nodo: la somma delle correnti entranti in un nodo è uguale alla somma delle correnti uscenti da esso.
Otteniamo il sistema di 4 equazioni in 4 incognite (semplificato con z = 1 m), che risolviamo nell’incognita Ti:
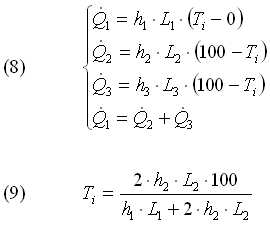
Notiamo che allo stesso risultato si poteva pervenire semplificando la rete, risolvendo il parallelo:
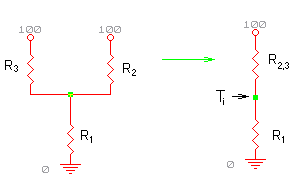
Figura 5
- Rete elettrica semplificata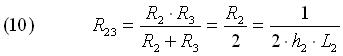
E applicando la regola del partitore di tensione:
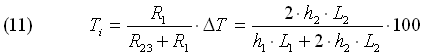
Calcoliamo ora i coefficienti di convezione h1 e h2 separando i due casi.
Calcolo di h1
Al solito il calcolo del coefficiente di convezione passa attraverso il numero di Nusselt riferito in questo caso alla parete piana 1, e che chiameremo Nu1.
Sfrutteremo infatti la relazione (1):
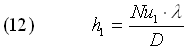
Dopodiché per calcolare il numero di Nusselt ci avvaliamo della relazione (4) per la convezione naturale:
![]()
In seguito calcoleremo i numeri di Grashof e Prandtl per determinare poi i parametri a, b, c attraverso il numero di Rayleigh.
Numero di Grashof
Utilizzeremo nel nostro calcolo la relazione generale (14):
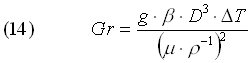
Notiamo da subito che n , l e Pr dipendono direttamente dalla temperatura incognita Ti . E’ chiaro, dunque, che Gr1 e successivamente Ra1 possono essere calcolati solo dopo aver fissato un valore di primo tentativo di Ti; dopodiché itereremo il processo di calcolo fino a che Ti non converge con sufficiente precisione.
Fissiamo allora Ti* = 330°K= 57°C (attenzione: l’apice indica il numero di
tentativo)
Estraiamo dalla tab. 2 le proprietà dell’aria che si trova a 57°C:
Proprietà dell’aria a 57°C:
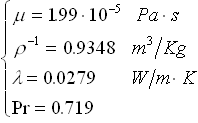
La dimensione caratteristica D, è in questo caso la larghezza della parete.
D=L1 =2 m
Ricordando poi che per un gas perfetto, quale viene assunta l’aria, che si trova alla temperatura T (espressa in Kelvin) vale:
![]() Nel nostro caso T= Ti* quindi
Nel nostro caso T= Ti* quindi
Tabella 2
– Proprietà termofisiche dell’aria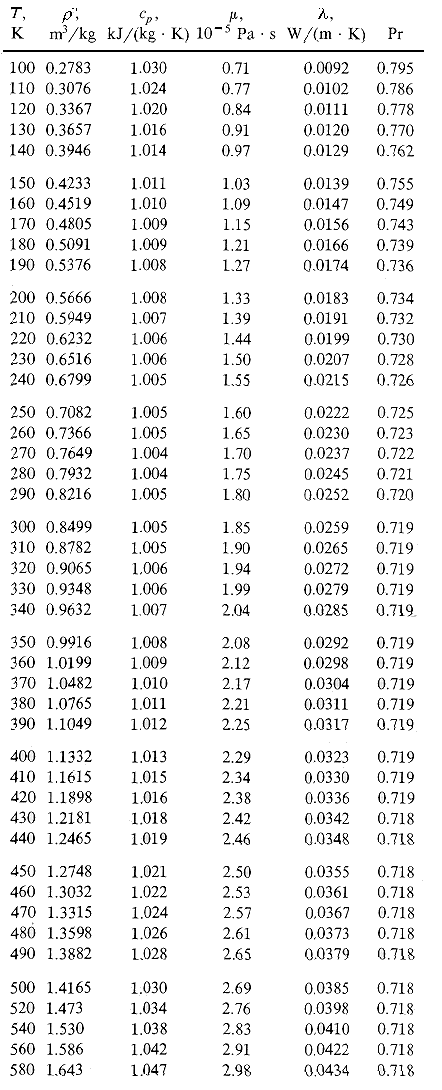
Calcoliamo Gr1:
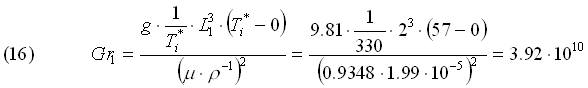
Numero di Rayleigh
A questo punto calcoliamo il numero di Rayleigh Ra1 tramite la (5):
![]()
Consultiamo la tab. 1, riferendoci ad una parete piana orizzontale: otteniamo, secondo Fishenden e Saunders, che il moto è turbolento e il seguente set di parametri:
a =0.33
b =0.33
c =0.14
Numero di Nusselt e coefficiente h1
Calcoliamo infine il numero di Nusselt e il coefficiente h1:
![]()
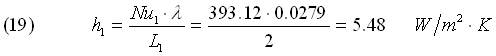
Calcolo di h2
Il calcolo di h2 è del tutto analogo a quello di h1, perciò ometteremo commenti ripetitivi.
Numero di Grashof
Abbiamo sempre Ti* = 57°C
e gli stessi valori di:
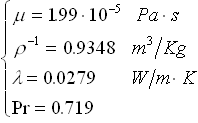
Mentre la dimensione caratteristica D, stavolta è l’altezza della parete.
D=L2 =1.5 m
Quindi abbiamo il numero di Grashof:
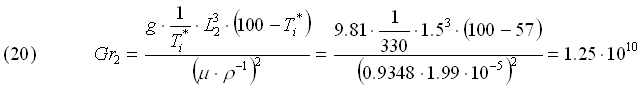
Numero di Rayleigh
![]()
Consultando la tab. 1 riferendoci ad una parete piana verticale, otteniamo, secondo Mc Adams, i valori:
a=0.33
b=0.33
c=0.13
Numero di Nusselt
Calcoliamo infine Nu2 e il coefficiente h2:
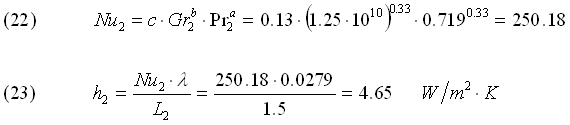
Temperatura Interna Ti*
Ricalcoliamo a questo punto il nuovo valore di Ti:
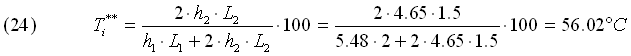
Come si osserva, il nuovo valore non coincide col valore imposto, pertanto è necessario rifare i calcoli con Ti*, utilizzando nuovi valori anche per n , l e Pr. Confrontando Ti** con Ti* osserviamo tuttavia che se iterassimo nuovamente il processo, otterremmo un valore che si discosta dai 56.02°C meno di 1°C; di conseguenza, in virtù della tolleranza di almeno il 20% che subiscono i risultati, potremmo già ritenerci soddisfatti. Tuttavia, iteriamo ugualmente il calcolo per illustrare il procedimento in maniera più completa e generale.
Come è facile notare dalla tab. 2, le proprietà dell’aria hanno una debole dipendenza dalla temperatura almeno per questi ranges di variazione di T; cosicché possiamo con ottima approssimazione ritenerle costanti., tanto più in base al discorso appena fatto. Facciamo intervenire la nuova Ti** solo nel calcolo del numero di Grashof. Seguono i risultati:
Numeri di Grashof
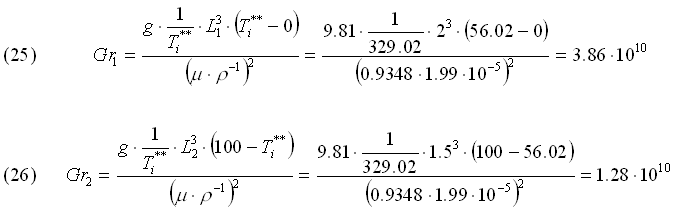
Numeri di Rayleigh
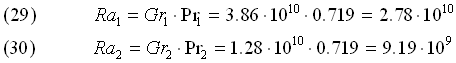
Se consultiamo la tab. 1 notiamo, come era facile prevedere, che i coefficiente a, b, c rimangono gli stessi: infatti dovendo Ti convergere, gli scostamenti di temperatura si riducono ulteriormente e i numeri di Rayleigh sono poco diversi tra loro.
Numeri di Nusselt e Coefficienti di Convezione
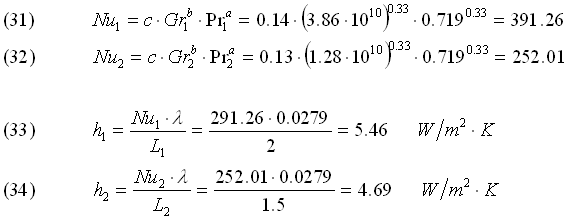
Temperatura Interna Ti**
Troviamo il definitivo valore di Ti .
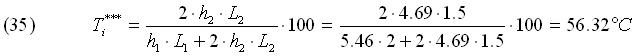
Esercizio 2 - Isolamento Anticondensa di una Tubazione
Descrizione del Problema:
Il tubo d’acciaio cilindrico in fig. 6 presenta un raggio interno r1 di 13 mm e un raggio esterno r2 di 17 mm. All’interno del condotto scorre acqua ad una temperatura TA di 5°C alla velocità di 1 m/s. All’esterno, si ha aria in quiete ad una temperatura ambiente TB di 20°C e grado igrometrico j B di 0,5. Rivestendo il tubo con una coppella di isolante (si assuma Poliuretano espanso) si vuole evitare la condensa sulla sua parete esterna. Calcolare la misura commerciale dello spessore di isolante sI, sufficiente a tale scopo.
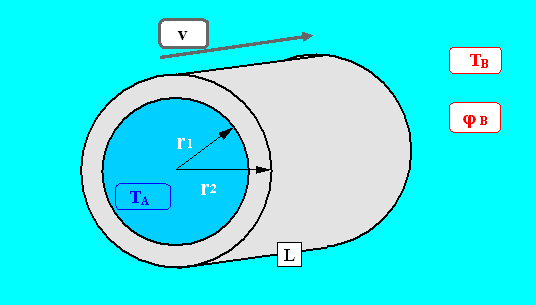
Figura 6
Dati del Problema:
Sul diagramma Psicrometrico in fig. 7, è stato evidenziato il punto di rugiada dell’aria all’esterno del tubo: come si vede la temperatura di rugiada è di circa 9°C.
Come è facile prevedere, la superficie esterna del tubo si porterà ad una temperatura non troppo distante dai 5°C dell’acqua; questo significa che su di essa si formerà effettivamente una condensa di vapor acqueo.
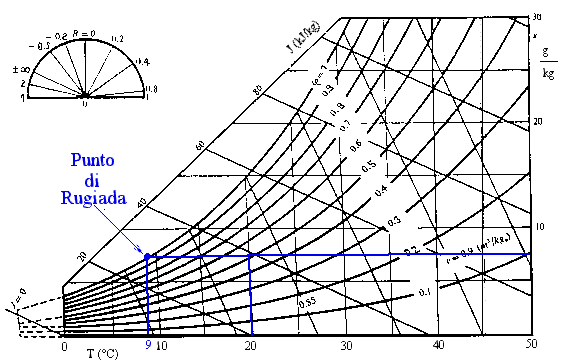
Figura 7
- Diagramma psicrometrico a pressione atmosfericaPer prima cosa osserviamo che il nostro scopo è determinare il valore commerciale minimo dello spessore di poliuretano, per ragioni di risparmio economico.
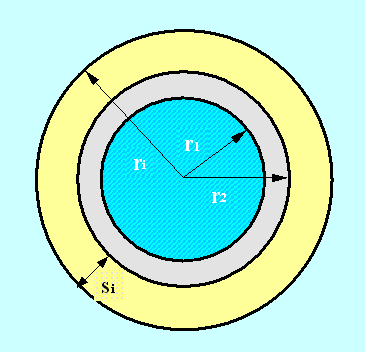
Figura 8
- Sezione del tubo rivestito di isolanteIn secondo luogo, dobbiamo imporre che la temperatura della parete esterna dell’isolante (TPE ) si porti ad un valore superiore ai 9°C.
Imponiamo dunque TPE ³ 9°C. Nel calcolo utilizzeremo:
TPE =10°C
Circuito Elettrico Equivalente
Passiamo ora all’Equivalente Elettrico: abbiamo 4 effetti di scambio termico, e relative 4 resistenze termiche:
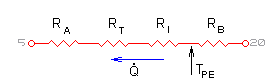
Figura 9
- Rete elettrica equivalente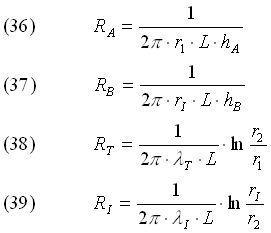
Siccome sI appare nelle direttamente nelle relazioni scritte (rI = r2 + sI), è necessario fissarne il valore affinché si possano calcolare le resistenze per scoprire così, ricalcolando TPE, se lo spessore è sufficiente o meno.
Con riferimento alla tab. 3 e tab. 4 scegliamo quindi il minimo spessore consentito sI e le proprietà dell’isolante.
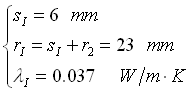
|
Tabella 3 – Proprietà del poliuretano espanso |
|
|
Caratteristiche Tecniche |
Valori/Valutazioni |
|
Composizione |
Schiuma di Poliuretano |
|
Temperature di Impiego |
Da -50°C a +110°C |
|
Conduttività termica alla temperatura media di 10°C |
l £ 0.037 (W/m K) |
|
Conduttività termica alla temperatura media di 40°C |
l £ 0.040 (W/m K) |
|
Coefficienti di resistenza alla diffusione del vapore |
m ³ 3 000 |
|
Comportamento al fuoco |
Classe 1 |
|
Tabella 4 – Misure commerciali dei rivestimenti per tubi in poliuretano espanso |
||||||||
|
Tubi di Acciaio |
Spessore (mm) |
|||||||
|
Diametro Pollici |
diametro mm |
6 |
9 |
13 |
19 |
25 |
32 |
|
|
1/8 |
10.2 |
· |
· |
|||||
|
1/4 |
13.2 |
· |
· |
· |
· |
· |
· |
|
|
3/8 |
17.2 |
· |
· |
· |
· |
· |
· |
|
|
1/2 |
21.3 |
· |
· |
· |
· |
· |
· |
|
|
3/4 |
26.9 |
· |
· |
· |
· |
· |
· |
|
|
30 |
· |
· |
· |
· |
· |
· |
||
|
1 |
33.7 |
· |
· |
· |
· |
· |
· |
|
|
1 1/4 |
42.4 |
· |
· |
· |
· |
· |
· |
|
|
1 1/2 |
48.3 |
· |
· |
· |
· |
· |
· |
|
|
2 |
60.3 |
· |
· |
· |
· |
· |
· |
|
|
63.5 |
· |
· |
· |
· |
· |
· |
||
|
70 |
· |
· |
· |
· |
· |
· |
||
|
· = Disponibile sul mercato |
||||||||
Calcoliamo di seguito i coefficienti di convezione
Calcolo di hA
Come sempre ricorriamo al numero di Nusselt. All’interno del tubo si ha scambio termico per convezione forzata, perciò sfrutteremo la già nota relazione:
![]()
Numero di Prandtl e proprietà dell’acqua
Assumiamo la temperatura dell’acqua a 5°C e consultiamo la tab. 5:
Proprietà dell’acqua a circa 5°C
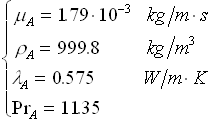
|
Tabella 5 - Proprietà Termofisiche dell’Acqua |
||||||
|
Temperatura |
Calore Specifico (p cost) |
Densità |
Viscosità Dinamica |
Conduttività Termica |
Numero di Prandtl |
|
|
T |
cp |
r |
m |
l |
Pr |
|
|
°F |
°C |
KJ/kg× °K |
kg/m3 |
kg/m× s × 10-3 |
W/m× °K |
|
|
32 |
0 |
4.225 |
999.8 |
1.79 |
0.566 |
13.25 |
|
40 |
4.44 |
4.208 |
999.8 |
1.55 |
0.575 |
11.35 |
|
50 |
10 |
4.195 |
999.2 |
1.31 |
0.585 |
9.40 |
|
60 |
15.56 |
4.186 |
998.6 |
1.12 |
0.595 |
7.88 |
|
70 |
21.11 |
4.179 |
997.4 |
0.98 |
0.604 |
6.78 |
|
90 |
26.67 |
4.179 |
995.8 |
0.86 |
0.614 |
5.85 |
|
100 |
32.22 |
4.174 |
994.9 |
0.765 |
0.623 |
5.12 |
|
110 |
37.78 |
4.174 |
993.0 |
0.682 |
0.630 |
4.53 |
|
120 |
43.33 |
4.174 |
990.6 |
0.616 |
0.637 |
4.04 |
|
121 |
48.89 |
4.174 |
988.8 |
0.562 |
0.644 |
3.64 |
|
130 |
54.44 |
4.179 |
985.7 |
0.513 |
0.649 |
3.30 |
|
140 |
60 |
4.179 |
983.3 |
0.471 |
0.654 |
3.01 |
|
150 |
65.55 |
4.183 |
980.3 |
0.43 |
0.659 |
2.73 |
|
160 |
71.11 |
4.186 |
977.3 |
0.401 |
0.665 |
2.53 |
|
170 |
76.67 |
4.191 |
973.7 |
0.372 |
0.668 |
2.33 |
|
180 |
82.22 |
4.195 |
970.2 |
0.347 |
0.673 |
2.16 |
|
190 |
87.78 |
4.199 |
966.7 |
0.327 |
0.675 |
2.03 |
|
200 |
93.33 |
4.204 |
963.2 |
0.306 |
0.678 |
1.90 |
|
220 |
104.4 |
4.216 |
955.1 |
0.267 |
0.684 |
1.66 |
|
240 |
115.6 |
4.229 |
946.7 |
0.244 |
0.685 |
1.51 |
|
260 |
126.7 |
4.250 |
937.2 |
0.219 |
0.685 |
1.36 |
|
280 |
137.8 |
4.271 |
928.1 |
0.198 |
0.685 |
1.24 |
|
300 |
148.9 |
4.296 |
918.0 |
0.196 |
0.684 |
1.17 |
Numero di Reynolds
Stabiliamo il regime di moto dell’acqua mediante il numero di Reynolds.
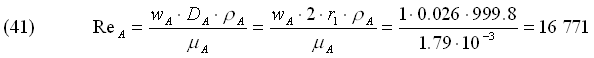
Osserviamo che Re =16 771 > 10 000 quindi il moto è turbolento. Dalla tab. 6 otteniamo la formula sperimentale per un fluido riscaldato, fornita da Dittus e Boelter, per il calcolo di NuA .
a = 0.8
b = 0.4
c = 0.023
![]()
Numero di Nusselt e Coefficiente hA
Infine otteniamo:
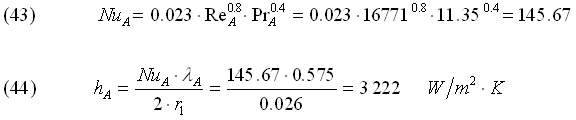
Tabella 6 -
- Formule sperimentali per il calcolo del numero di Nusselt: convezione forzata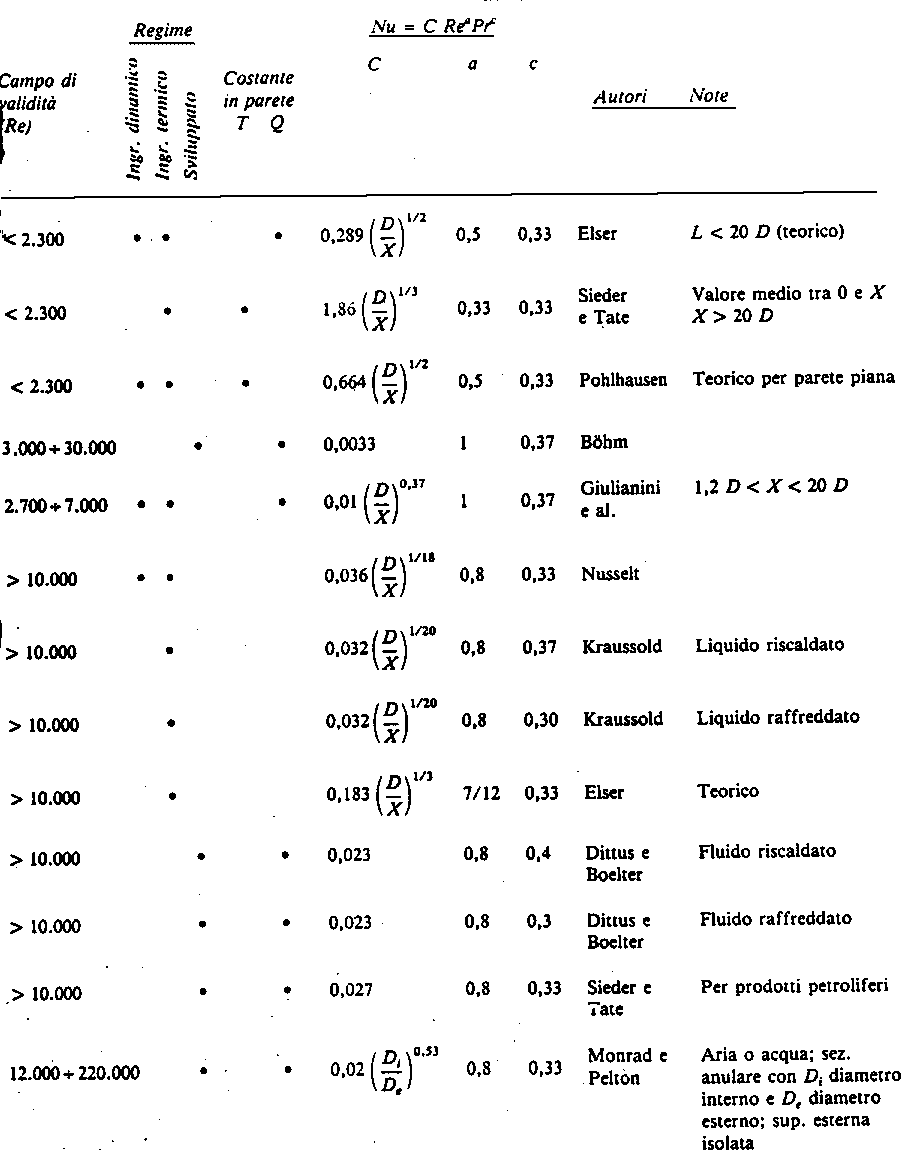
Calcolo di hB
All’esterno del tubo rivestito, l’aria non subisce alcun moto forzato, di conseguenza si ha scambio termico per convezione naturale. Sfruttiamo dunque la relazione (4) per il calcolo del numero di Nusselt NuB:
![]()
Numero di Grashof
Stabiliamo convenzionalmente di prendere l’aria coinvolta nello scambio termico ad una temperatura intermedia tra quella di parete e quella del fluido non perturbato, in modo da poter ricavare le sue proprietà.
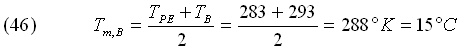
Dalla tab. 2 ricaviamo il set di valori per una temperatura di circa 15°C:
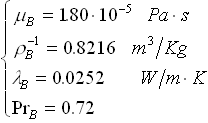
L’aria viene idealmente considerata un gas perfetto, quindi calcoliamo nel seguente modo il coefficiente di dilatazione termica:
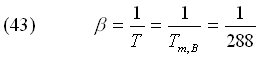
Calcoliamo GrB attraverso la (5):
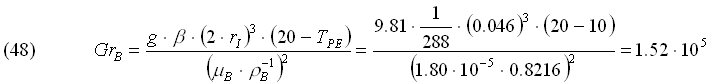
Numero di Rayleigh
A questo punto calcoliamo il numero di Rayleigh RaB:
![]()
Consultiamo la tab. 1, riferendoci ad una superficie cilindrica orizzontale. Otteniamo secondo Mc Adams, i tre parametri:
a =0.53
b =0.25
c =0.25
Numero di Nusselt
Calcoliamo infine il numero di Nusselt e il coefficiente hB:
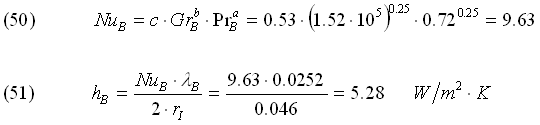
Proprietà dell’Acciaio
Riportiamo dalla tab. 7 la conduttività dell’acciaio:
|
Tabella 7 - Proprietà Termofisiche di Metalli e Leghe |
||||||
|
Materiale |
Conduttività Termica |
Calore Specifico (p cost) |
Densità |
|||
|
l W/m× °K |
cp kJ/kg× °K |
r kg/m3 |
||||
|
0°C |
100°C |
300°C |
500°C |
0°C |
0°C |
|
|
Acciaio |
45 |
45 |
43 |
39 |
0.460 |
7850 |
|
Alluminio |
202 |
205 |
226 |
259 |
0.870 |
2710 |
|
Argento |
420 |
423 |
0.240 |
10500 |
||
|
Ferro, puro |
62 |
63.2 |
0.435 |
7870 |
||
|
Ghisa, pura |
57 |
55 |
51 |
47 |
0.460 |
7590 |
|
Oro |
292 |
294 |
0.126 |
19270 |
||
|
Ottone |
96.5 |
102 |
111 |
0.385 |
8520 |
|
|
Piombo |
35 |
33 |
32 |
0.126 |
11290 |
|
|
Platino |
70 |
73 |
0.131 |
21400 |
||
|
Rame |
387 |
376 |
368 |
360 |
0.381 |
8940 |
Resistenze Termiche e TPE
Siamo ora in grado di quantificare tutte le resistenze termiche a meno della lunghezza del tubo:
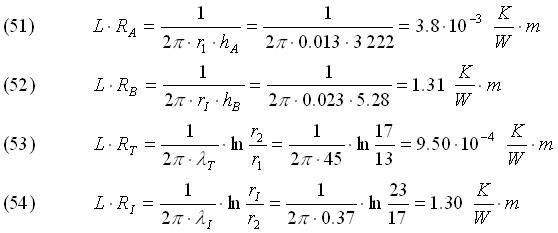
Risolviamo la rete elettrica: riconosciamo subito che le 4 resistenze sono in serie, il che ci permette di trovare la potenza termica per unità di lunghezza del tubo:
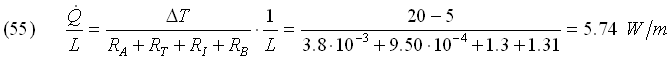
Infine ricalcoliamo la temperatura della parete esterna dell’isolante TPE: dalla fig. 9 vediamo che possiamo utilizzare la legge di Ohm per il resistore RB:
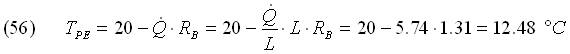
La temperatura trovata non coincide con i 10°C imposti, tuttavia essa supera la stessa temperatura pur avendo impiegato il minimo spessore di isolante commercialmente disponibile. Questo risultato, peraltro particolarmente favorevole, conclude l’esercizio:
Spessore di isolante utilizzato: sI = 6 mm
Diametro esterno dell'isolante: rI = 23 mm