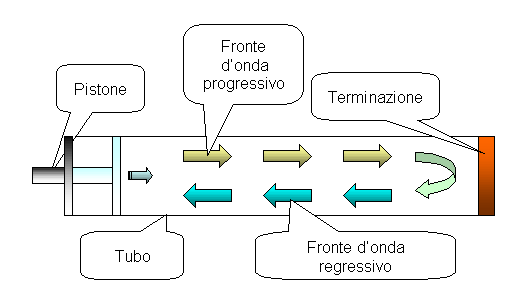
Al fine di studiare le onde stazionarie prendiamo in considerazione un esempio pratico di facile fruizione cioe’ un tubo di lunghezza finita caratterizzato da una terminazione rigida ad un’estremita’ e da un pistone all’altra; la funzione del pistone sara’ quella di generare un tipo di onda stazionaria diretta verso la terminazione rigida.

Figura 1. Schema del tubo

In questa situazione l’onda sonora, una volta giunta alla fine del tubo, verra’ respinta generando un’onda riflessa indirizzata in senso contrario. Se considerassimo una sezione del condotto ad un’ascissa generica "x" potremmo rilevare la presenza di un fronte d’onda progressivo diretto da sinistra verso destra e di un fronte d’onda regressivo da destra verso sinistra. Come conseguenza di questo fatto avremo un particolare tipo di soluzione dell’equazione di Helmoltz:

Il potenziale della velocita’ "F " risultera' composto da una parte "positiva" e da una parte "negativa". Analizzando il primo termine della (1) possiamo notare che l’argomento dell’esponenziale cioe' "(w t -kx)" viene mantenuto costante per x crescenti al variare del tempo, quindi se intendiamo ritrovare un segnale osservato all’istante "t" nell’istante successivo "t+1" dovremo incrementare la x; possiamo concludere che il fronte d’onda rappresentato da questo primo termine sara’ diretto nel verso delle ascisse crescenti. Questa analisi puo’ essere ripetuta similmente per il secondo termine della (1); quest’ultimo rappresentera’ un fronte d’onda che viaggera’ in senso opposto rispetto al primo (questa volta il termine kx e’ presente con il segno +) .

Sappiamo che la velocita’ e la pressione sono legati al potenziale della velocita’ tramite due espressioni; la prima attraverso il gradiente spaziale, che in questo caso si riduce ad una derivata semplice perche’ ci troviamo in una situazione monodimensionale, la seconda tramite la relazione di Eulero. Quindi possiamo ricalcolare facilmente entrambe le grandezze sfruttando la (1):

Dovendo applicare opportune condizioni al contorno alla soluzione dell’equazione di Helmoltz avremo come conseguenza diretta condizioni anche sulle due espressioni di velocita’ e pressione; per esempio occorrera’ imporre una certa velocita’ dell’onda sonora in corrispondenza del pistone mobile ed un’altra sulla terminazione rigida.

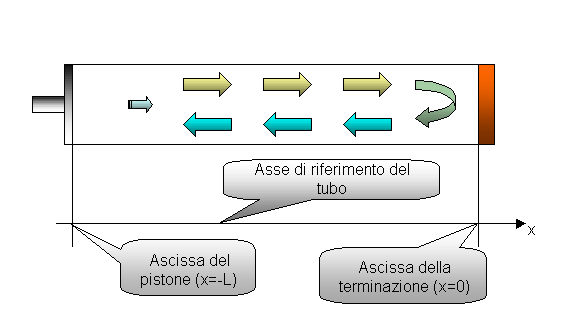
Figura 2. Mostra l'asse di riferimento sul tubo.

Le due condizioni al contorno da utilizzare saranno le seguenti:

1. In corrispondenza del pistone mobile (quindi per x=0, se prendiamo come riferimento quello di figura 2) la velocita’ assumera’ un particolare valore finito u_max;
2. In corrispondenza della terminazione rigida del tubo (quindi per x=-L) il valore della velocita’ sara’ nullo.

Teniamo presente che in questo momento stiamo considerando il caso in cui si abbia una terminazione rigida cioe’ che presenti un’ impedenza infinita (infatti l’impedenza e’ data dal rapporto tra pressione e velocita’; se ipotizziamo una velocita’ nulla sulla terminazione, qui tale rapporto tendera’ a piu’ infinito); in seguito ci occuperemo del caso ben piu’ interessante in cui la parte finale del condotto sia caratterizzata da un valore di impedenza finito non nullo.

Ricalcolando l’espressione (3) della velocita’ e imponendo x=0 otteniamo:

Alla luce di questo risultato si intusce facilmente che il termine ï F ï dipende dalla velocita’ massima imposta nel punto di eccitazione del sistema (quindi dove e’ situato il pistone), percio’ il passo successivo sara’ calcolare ancora una volta l’espressione (3) della velocita’, stavolta imponendo x=-L ricavando:

Dalla (5) sono in grado di estrapolare il valore del potenziale della velocita’ che rende vera l’equazione di Helmoltz (nella trascrizione della (5) e’ stato trascurato volutamente il termine "e^{iw t} " perche’ comunque ci interessa valutare il valore massimo della velocita’).

Il discorso appena fatto illustrava i passaggi squisitamente matematici del discorso, ma nella pratica e’ interessante cercare di avere un’idea di cio’ che accade spazialmente all’interno del tubo.

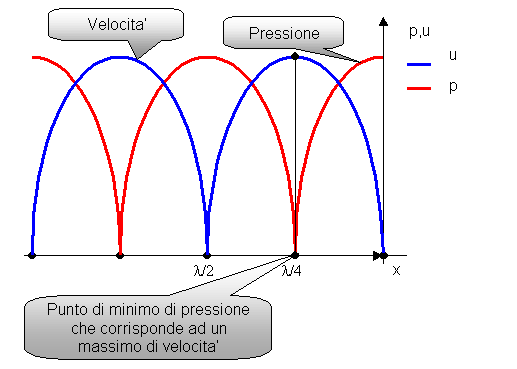
Figura 3.a. Mostra l'andamento della pressione e della velocita' nel tubo.

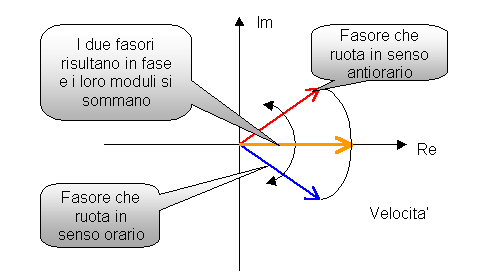
Figura 3.b. Mostra sul piano complesso l'andamento dei due fasori.

Analizzando il grafico di figura 3.a, in cui sono rappresentate la pressione e la velocita’ in funzione dell’ascissa "x" nel tubo, si nota che nei punti dove si ha velocita’ massima la pressione assume valore nullo e viceversa; questo fatto e’ dimostrabile per via matematica sul piano complesso. Infatti in figura 3.b vengono mostrati i due fasori che compaiono nell’espressione della velocita’; essi ruotano in senso opposto l’uno rispetto all’altro a causa del segno contrario dei rispettivi argomenti e ad ogni quarto di lunghezza d’onda (l /4) si ritrovano sfasati di 180 gradi. In questi punti la risultante tra i due e’ data dalla differenza dei moduli e quindi rappresenta un minimo della velocita’. Analogamente, nei punti in cui i due vettori sono in fase, la risultante sara’ data dalla somma dei moduli e rappresentera’ un massimo.

Vediamo ora il caso in cui la terminazione del tubo non sia rigida cioe’ l’impedenza del materiale usato per chiudere il condotto sia un valore finito e non nullo. In questa nuova situazione non sara’ piu’ vero che la velocita’ sulla terminazione si annulla e quindi non sara’ piu’ vero che ï F _{+ï = ï F -ï} =ï F ï .

Per definire al meglio cosa accade e’ necessaria l’espressione dell’impedenza:

Dalla (6) si vede che "z" e’ una grandezza che varia lungo il tubo; lo si capisce anche osservando il grafico 3.a, infatti ogni quarto di lunghezza d’onda il suo valore oscilla tra zero e infinito. Tenendo presente queste considerazioni diventa molto delicata la scelta della posizione del pistone mobile all’interno del tubo perche’ e’ chiaro che tale scelta influenzera’ le caratteristiche del sistema. Se il pistone dovesse essere posizionato in una zona a impedenza infinita allora con una velocita’ piccolissima si produrrebbe una pressione incredibile e avremmo la situazione favorevole di massimo trasferimento di energia. Se viceversa il pistone dovesse essere inserito in una zona con impedenza nulla (quindi velocita’massima e pressione nulla) avremmo la sgradevole situazione di trasferimento di energia nullo (per rendere l’idea sarebbe come avere una molla che non risponde alle sollecitazioni). In qualsiasi altra posizione avremmo un trasferimento di energia intermedio tra zero e infinito. E’ ovvio che una situazione del genere sarebbe decisamente instabile, in particolar modo alle alte frequenze dove la lunghezza d’onda risulerebbe piccola; se sfortunatamente la corsa del pistone dovesse essere confrontabile con questo valore il pistone, nel suo avanzare, si troverebbe in zone a differente impedenza. Conseguenza di cio’ sarebbe la non linearita’ del sistema.

L’esempio di cui ci siamo occupati fino a questo momento e i discorsi ad esso collegati non troverebbero applicazioni pratiche se l’impedenza della terminazione del tubo fosse infinita; il riscontro concreto a tutta questa teoria lo si ha quando il valore di "z" e’ finito e non nullo ed e’ incognito. In questo situazione, attraverso una misurazione di pressione sonora lungo il condotto, e’ possibile risalire a tale grandezza .

Iniziamo la trattazione di questo nuovo caso riformulando l’espressione (6) della pagina precedente sostituendo la pressione al posto del potenziale della velocita’ F dato che tra le due grandezze sussiste un rapporto di proporzionalita’ diretta (tale rapporto esisterebbe anche con la velocita’, ma e’ preferibile utilizzare la pressione perche’ piu’ semplice da misurare). Quindi consideriamo

A fronte del fatto che l’impedenza della terminazione non e’ piu’ infinita osserveremo un cambiamento nell’andamento della pressione nel tubo cioe’ il punto nel quale si aveva pressione massima e velocita’ minima non sara’ piu’ nella stessa posizione, ma risultera’ spostato; inoltre la velocita’ minima come la pressione non saranno piu' zero, ma un valore differente. La situazione si mostrera’ sicuramente meno chiara, ma, per esempio, muovendoci con il microfono lungo il condotto avremo comunque dei picchi nel profilo della pressione. Allora supponiamo di considerare una zona centrale del condotto dove la pressione avra’ questo tipo di andamento:

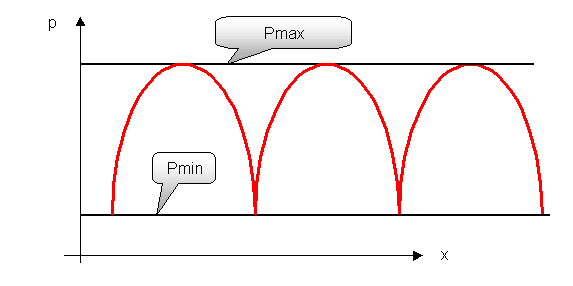
Figura 4. Mostra l'andamento della pressione in una zona centrale del tubo.

Pur essendo un grafico qualitativo, che intende dare solo un’idea del muoversi della pressione, si puo’ evincere che la misurazione del valore massimo di pressione risultera’ piu’ agevole rispetto alla ricerca dei valori minimi. Tutto cio’ e’ dovuto alla forma del grafico in figura (4), infatti vicino ai massimi la curva si mostra dolce e un semplice spostamento a mano del microfono per le misurazioni di pressione consentira’ di trovare il valore cercato; in prossimita’ dei minimi la curva si fa ripida e quindi si dovra’ ricorrere a strumenti piu’ precisi della "mano umana" per effettuare la misurazione (specialmente alle alte frequenze dove la lunghezza d’onda e’ piccola).

Comunque al di la’ di questi problemi tecnici sappiamo estrapolare le relazioni tra i valori di p_min e p_max e i due fattori p₊ e p_- che comparivano nella (7). Impostando un sistema con queste due espressioni e’ possibile ricavare il rapporto tra p_max e p_min che tornera’ molto utile in seguito nel proseguimento del discorso.

E' importante notare che l’impedenza del materiale utilizzato come terminazione dovrebbe essere quella valutata esattamente alla fine del tubo (cioe’ quando x=0) e utilizzando l’espressione di "z" con la pressione (formula (7)) otterremmo:

Quest’ultima fornisce un’impedenza reale, ma nella pratica le impedenze dei materiali sono dei valori complessi (questo perche’ in generale pressione e velocita’ sono sfasate). Quindi la (9) in realta’ mette a disposizione solo il modulo dell’impedenza; per avere anche la fase di questa grandezza occorre calcolare la distanza tra la terminazione e il punto di pressione massima (ora siamo nel caso di impedenza finita e quindi il valore massimo della pressione non si avra’ piu’ in corrispondenza della terminazione).

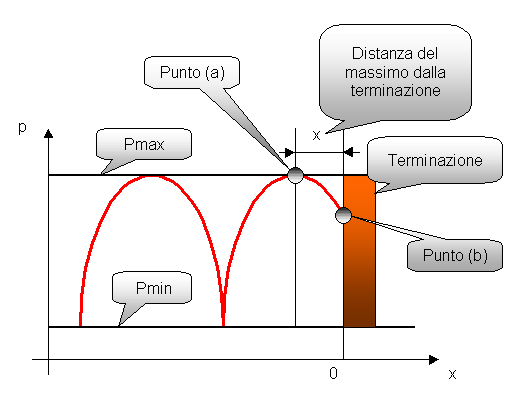
Figura 5. Mostra in che misura il massimo di pressione risulta spostato dalla terminazione.

Nel punto (a) della figura 5 la "z" risulta reale (i due fasori prima citati sono in fase e i loro moduli si sommano dando luogo ad un massimo); nel punto (b) invece la "z" e’ ruotata di un fattore "e^i2kx". Esprimeremo quindi l’impedenza come:

Da quest’ultima analisi si deduce che l’impedenza non e’ una grandezza molto maneggevole, in particolare nel caso delle onde piane progressive dove la sua fase varia; nella pratica cio’ che viene maggiormente usato nella trattazione di questi problemi e’ il coefficiente di assorbimento acustico "a ", un parametro puramente energetico che rappresenta l’energia dell’onda riflessa rapportata all’energia dell’onda progressiva, insieme al coefficiente di riflessione "r".

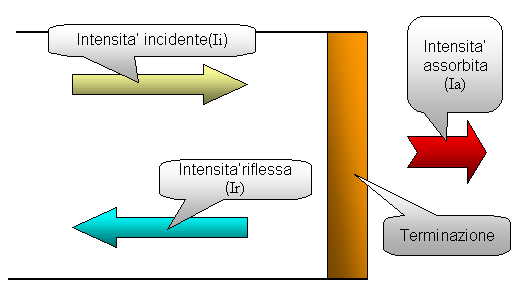
Figura 6. Mostra uno schema del tubo con le quote di energia.

Come si vede in figura (6) quando l’onda sonora si infrange contro la terminazione una quota di energia viene riflessa e l’altra parte viene assorbita. Definiamo quindi il coefficiente a come:

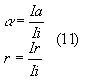
Solitamente ci si occupa di calcolare prima "a " e in un secondo momento di ricavare "r" di conseguenza sfruttando le relazioni descritte nella (11).

Definiamo adesso il rapporto di riflessione complesso, una nuova grandezza che, attraverso le formule dell’impedenza, ci permettera’ di valutare il coefficiente di assorbimento acustico.

Riprendendo la (9) scopriamo che il rapporto di riflessione complesso era presente nell’espressione sotto forma di rapporto tra "p_- "e "p₊ " infatti:

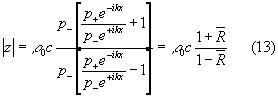
E’ percio’ possibile invertire il procedimento e ricavare il rapporto di riflessione complesso in funzione dell’impedenza:

Ci accorgiamo che il coefficiente di riflessione "r" definito prima nella (11) altro non e’ che il rapporto di riflessione complesso elevato al quadrato, quindi sostituendo questa relazione nell’equazione del coefficiente di assorbimento acustico (formula (11)):

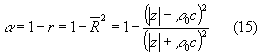
Il risultato al quale arriviamo e’ l’impedenza puo’ servire nel calcolo del coefficiente di assorbimento acustico.

Adesso riprendiamo il rapporto p_max su p_min estrapolato dalla (8) chiamandolo "n". Scopriamo che il rapporto di riflessione complesso e’ funzione di questparametro "n" secondo la seguente legge:

Qui e’ evidenziata anche la dipendenza dal termine x (distanza del punto di massimo di pressione dalla terminazione del tubo). Questa dipendenza puo’ essere evitata sostituendo la (16) nella (13) ricavando "a " in funzione di "n":

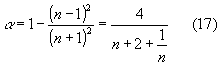
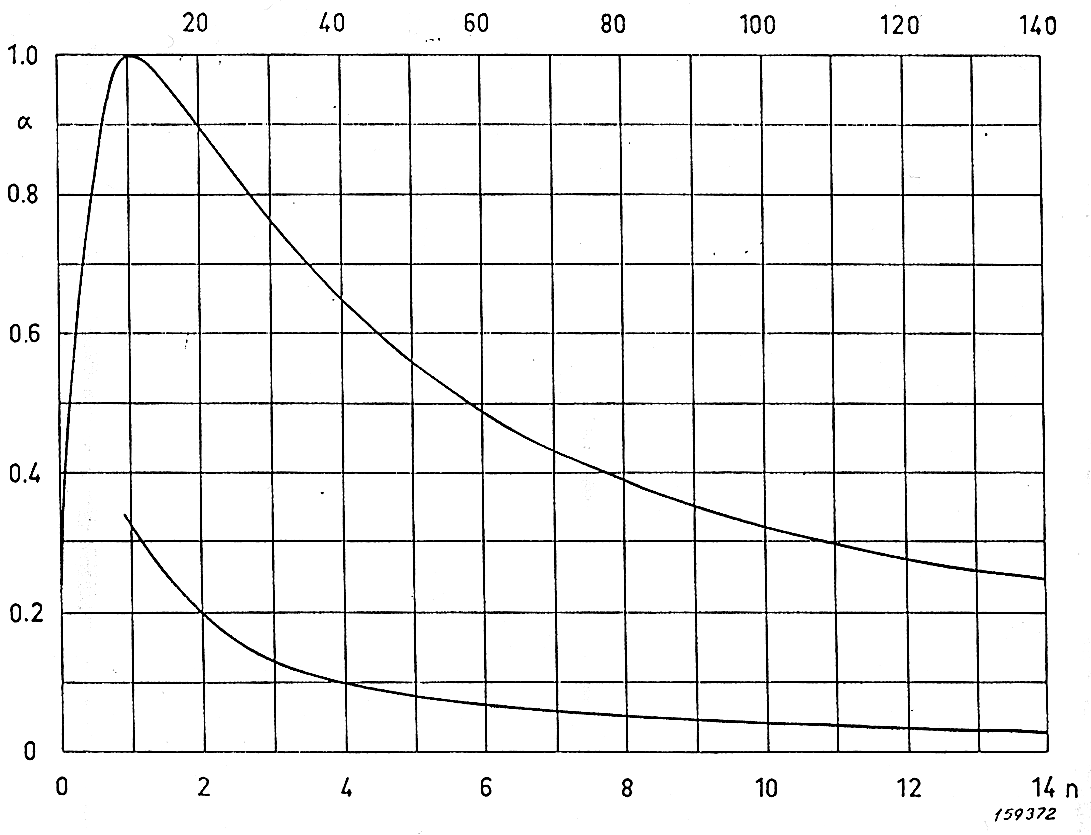
Figura 7. Mostra l'andamento di alfa in funzione di n.

In figura (7) viene mostrato l’andamento del coefficiente di assorbimento in funzione del rapporto tra p_max e p_min cioe’ "n" (nel grafico sopra mostrato la scala viene interrotta e ripresa per problemi di spazio).

Ovviamente tutti questi passaggi evidenziano il fatto che il cofficiente di assorbimento puo’ essere calcolato direttamente dal rapporto tra p_max e p_min, disinteressandosi di "z". Nel qual caso occorresse calcolare l’impedenza e’ possibile farlo tramite questa relazione:

Nella (18) compare un termine x_min che rappresenta la distanza di un punto di minima pressione dalla terminazione del tubo; ci interessa conoscere questa distanza perche’ occorre mettersi in un punto dove i due fasori contenuti nell’espressione della pressione siano in fase e dove "z" sia reale (vedi figura (8)). Tutto cio’ avviene quando la velocita’ e’ massima e la pressione e’ minima; il termine x_min presente nella (18) si riferisce proprio al fatto che sto trattando un punto di minima pressione. Avrei potuto impostare i calcoli sulla posizione del massimo di pressione (l’impedenza sarebbe risultata comunque reale), ma la determinazione del punto di minimo e’ piu’ semplice e piu’ precisa di quella del punto di massimo per il profilo della pressione nel tubo (il minimo di pressione e’ un picco mentre il massimo e’ una curva dolce). Non importa a quale minimo facciamo riferimento perche’ l’angolo di fase dei due fattori citati non cambia con un numero intero di giri.

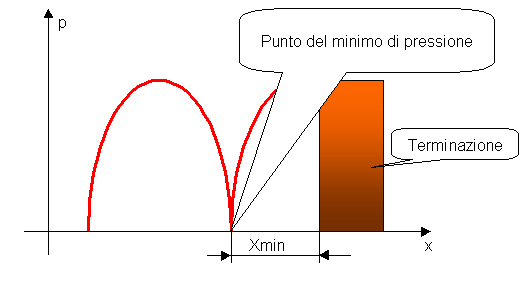
Figura 8. Mostra l'andamento della pressione evidenziando la distanza xmin dalla terminazione.

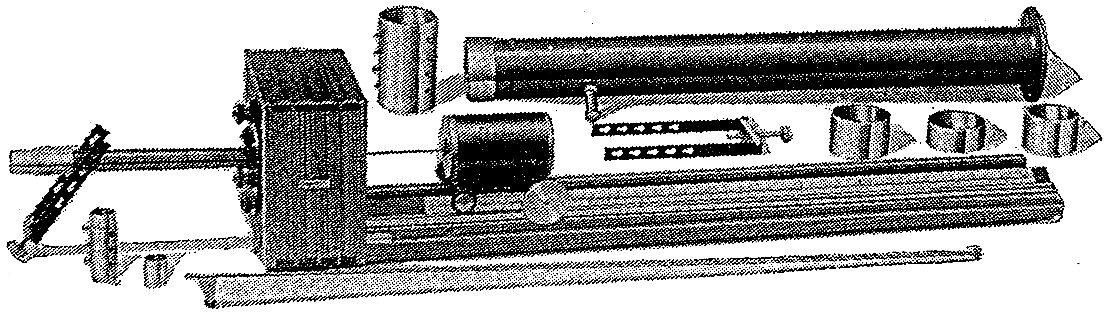
Figura 9. Mostra una macchina di Kundt.

In figura (9) e’ ritratta una macchina di Kundt o macchina ad onde stazionarie che serve per la misurazione della pressione sonora all’interno di un tubo. Si avvale della seguente strumentazione:

• Due tubi di acciaio di diametri differenti. Il piu’ piccolo (diametro di circa 29 mm ) serve per misurazioni ad alte frequenze, il secondo (diametro di circa 99 mm) serve per misurazioni a frequenze medio basse (fino a 1800 Hz);
• Bicchieri di diverse dimensioni;
• Provini (dischetti di materiali differenti che costituiscono la terminazione del tubo);
• Corpo centrale sul quale si distingue un altoparlante all’interno del quale scorre un tubicino che conduce ad un microfono montato su di un carrellino. Sulle ruote del carrello c’e’ una scala graduata che permette di misurare gli spostamenti fino al decimo di millimetro.

Il provino scelto viene inserito in uno dei bicchieri che a sua volta viene montato su uno dei due tubi e tramite una staffa viene premuto all’estremita’ del tubo.

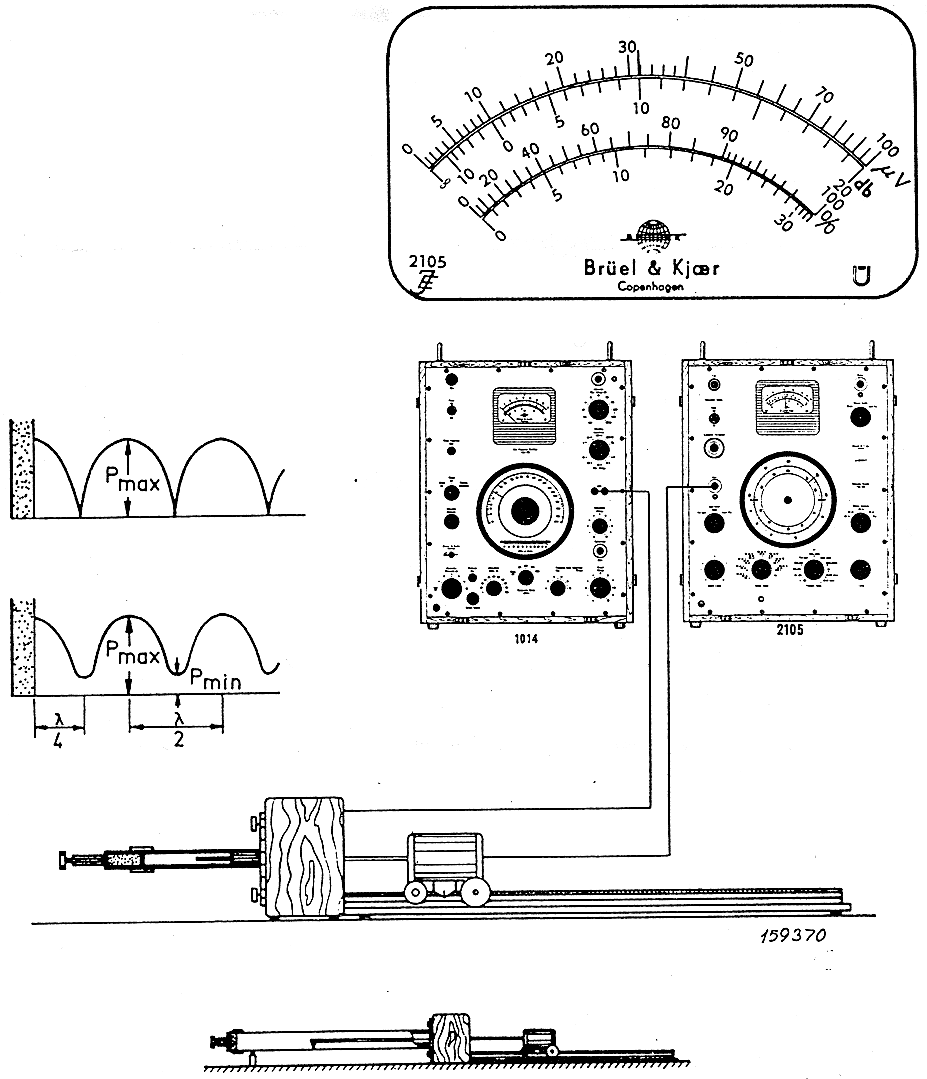
Figua 10. Mostra in quale modo viene montata la strumentazione relativa alla macchina di Kundt.

Come si vede dalla figura (10) viene collegato un voltmetro al microfono che misura un certo voltaggio corrispondente ad un valore di pressione della forma d’onda. Non e’ necessario calibrare il voltmetro perche’ comunque ci interessa solamente calcolare la pressione massima e quella minima e determinarne il rapporto. Collegato al tutto c’e’ un frequenzimetro che consente di ripetere l’esperimento a differenti frequenze.

E’ importante conoscere lo spessore del provino per tarare correttamente la posizione dello zero nella scala graduata; questa operazione e’ consentita grazie al supporto variabile che permette di spostare micrometricamente la superficie del provino.

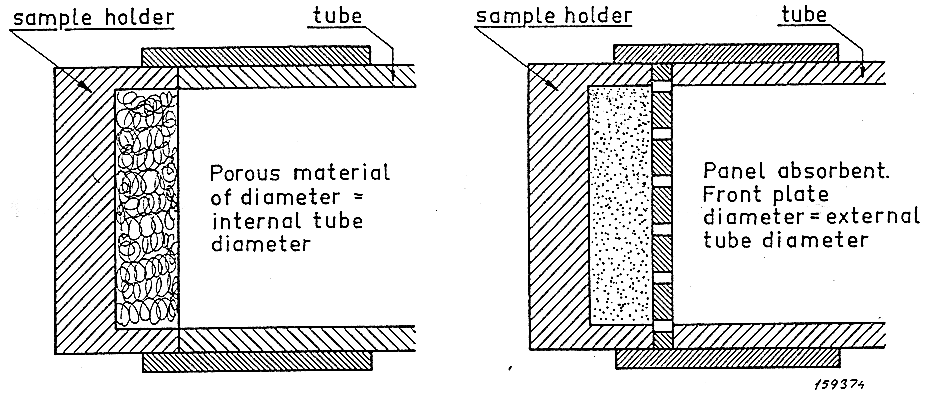
Figura 11. Particolare del bicchiere e del provino.

In figura (11) viene mostrato come si monta il provino all’interno del bicchiere e come si stima lo zero della scala graduata.

Una soluzione del genere per il calcolo del coefficiente di assorbimento non richiede una strumentazione complessa ne’ particolari cure nell’esecuzione dell’esperimento; e’ quindi un metodo che e’ stato molto utilizzato fino a poco tempo fa. Comunque cio’ non toglie che esista un sistema piu’ intelligente e piu’ rapido, anche se necessita di un tipo di apparecchiatura non comunissima, o almeno non cosi reperibile come la macchina di Kundt.

L’innovazione di questo procedimento risiede nel fatto che la soluzione si appoggia su base energetica ossia sulla misura di grandezze quali l’intensita’ sonora e la densita’delle molecole sonore.

Riprendiamo l’esempio del tubo di lunghezza finita con una terminazione caratterizzata da un particolare valore incognito del coefficiente di assorbimento.

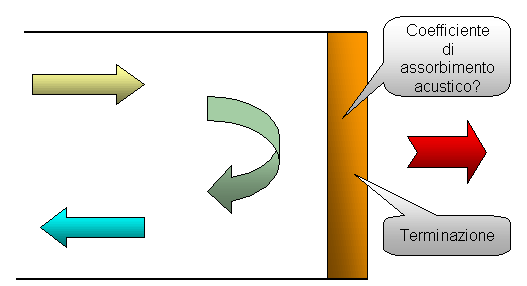
Figura 12. Il coefficiente di assorbimento acustico e' un'incognita.

Come mostrato in figura (12) all’interno del tubo ho una quota di energia incidente e una di energia riflessa. Se posizioniamo una sonda intensimetrica dentro al tubo non riusciamo a misurare separatamente intensita’ incidente e intensita’ riflessa, siamo solamente in grado di calcolarne la differenza cioe’:

Dato che la densita’ gode della proprieta’ additiva la posso vedere come somma dell’intensita’ parziale dell’onda incidente e quella dell’onda riflessa:

Impostando quindi un sistema con le due relazioni sopracitate ottengo:

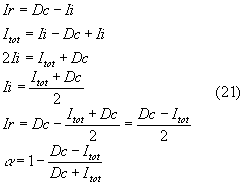
Siamo giunti ad esprimere il coefficiente di assorbimento acustico in funzione dell’intensita’ e della densita’. Possiamo spingerci oltre definendo un nuovo parametro:

Chiamiamo questo parametro velocita’ dell’energia acustica; si tratta di un vettore allineato con il vettore intensita’ dato che la densita’ e’ uno scalare. Il suo valore puo’ variare da zero (situazione in cui non c’e’ propagazione di energia) alla velocita’ del suono (il campo e’ tutto attivo); in pratica e’ un’indice di quanto il campo e’ reattivo.

Sulla base di questo nuovo vettore siamo in grado di definire il coefficiente di propagazione b :

Questo coefficiente e’ un parametro numerico che lo strumento e’ in grado di fornirci immediatamente; infine possiamo legare il coefficiente di assorbimento acustico al coefficiente di propagazione in questo modo:

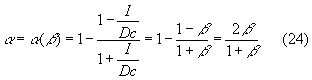
Un vantaggio non indifferente di questo tipo di soluzione e’ che ne’ la densita’ ne’ l’intensita’ dipendono dal punto di misura perche’ sono costanti nel tubo al contrario di pressione e velocita’. Quindi la sonda intensimetrica potra’ essere posizionata a piacimento lungo il condotto. Inoltre sono grandezze che possono valere su tutto lo spettro delle frequenze e quindi l’esperimento non deve essere ripetuto per ogni singola frequenza, ma puo’ essere effettuato una volta sola.