Indice
1. Esempi riguardanti lo scambio termico
1.1. Tubo rivestito da materiale isolante
1.2. Cavo elettrico percorso da corrente
2. Convezione naturale e convezione forzata
2.1. Convezione naturale
2.2. Convezione forzata pura e convezione mista
2.3. Scambio termico coniugato
2.4. Convezione a flusso di calore imposto e convezione a temperatura imposta
2.5. Tiraggio dei camini
1. Esempi riguardanti lo scambio termico
1.1. Tubo rivestito da un materiale isolante
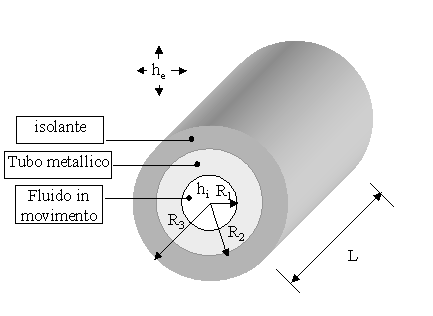
Si vuole fare lo studio di quello che accade in un tubo rivestito da un isolante (fig.1). Attorno al tubo cavo si mette un rivestimento di materiale isolante. Si realizza in questo modo uno strato cilindrico doppio, nel quale la superficie interna è normalmente realizzata con un materiale piuttosto conduttivo per il calore, in quanto metallico.
Viceversa attorno al tubo metallico si pone un rivestimento di materiale isolante, con una conducibilità termica molto più bassa, utile per due motivi:
La geometria è caratterizzata da 3 valori del raggio:
r1, raggio interno del tubo interno;
r2, raggio esterno del tubo metallico o raggio interno dell’isolante;
r3, raggio esterno dell’isolante.
Normalmente nel tubo interno c’è un fluido in movimento e quindi avviene un fenomeno di scambio convettivo.
Dove transita il fluido ci sarà un certo coefficiente di convezione interna hi, piuttosto elevato (hi=1000÷2000, in quanto vi è un fluido che scorre ad alta velocità); mentre all’esterno del tubo ci sarà un coefficiente di convezione esterna he, che invece normalmente è molto più piccolo (poiché siamo in aria ferma, e quindi in condizione di convezione naturale, he=8÷10).

Figura 1. Tubo metallico rivestito di materiale isolante
Vogliamo trovare la potenza dispersa, di questo tubo, considerando che ha una certa lunghezza L.
Utilizziamo le resistenze termiche (fig.2). Il calore partendo dal centro tubo, deve attraversare:
Calcoliamo i valori delle singole resistenze; utilizzando le formule ricavate nelle lezioni precedenti:
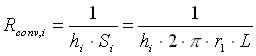 (1)
(1)
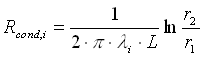 (2)
(2)
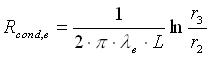 (3)
(3)
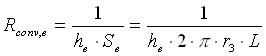 (4)
(4)
dove l i, l e, hi, he sono rispettivamente la conducibilità termica del tubo metallico e dell’isolante, e il coefficiente di convezione all’interno del tubo e all’esterno.
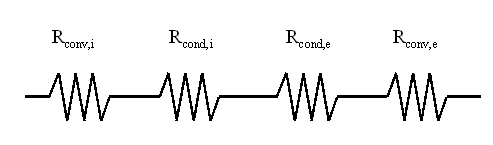
Figura 2. Rappresentazione mediante l'uso delle resistenze
Tali resistenze, essendo in serie, andranno a sommarsi.
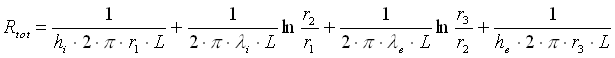 (5)
(5)
Quindi la potenza termica scambiata sarà uguale a:
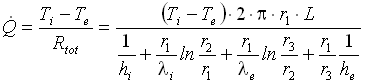 (6)
(6)
dove Ti e Te sono la temperatura del fluido all’interno e dell'aria all’esterno del tubo.
Questa formula la posso vedere utilizzando la formula con il coefficiente globale di scambio K
![]() (7)
(7)
dove:
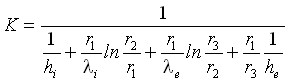 (8)
(8)
Si cerca, ora, di capire, come varia la potenza termica scambiata all’aumentare dello spessore dell’isolante.
Essendoci l’isolante, si potrebbe pensare che la potenza termica scambiata sia minore; invece normalmente cresce fino ad un valore massimo caratterizzato da una raggio critico rcritico, per poi decrescere asintoticamente fino al valore zero, come rappresentato nel grafico (fig.3).
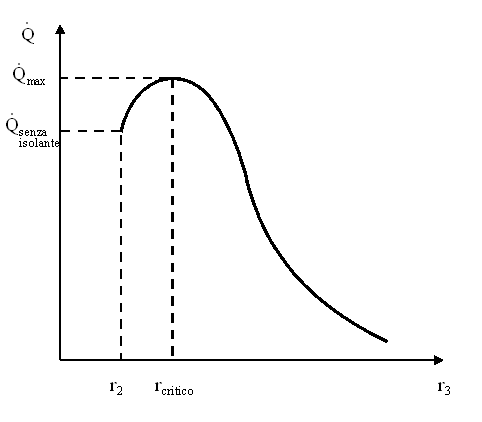
Figura 3. Potenza termica scambiata in funzione del raggio dell'isolante
Ciò è dovuto dal fatto che, nella formula per ricavare la potenza termica il termine r3 compare in due punti:
L’aumento di r3, e quindi della superficie di scambio, fa sì che la resistenza Rconv,e decresca, ed almeno inizialmente si abbia un aumento della potenza scambiata, finché la resistenza Rcond,e non cresce abbastanza da compensare la diminuzione di Rconv,e. La potenza termica scambiata cresce fino ad un valore limite denominato ![]() .
.
Quindi un isolante di spessore troppo piccolo, può addirittura essere controproducente, in quanto aumenta lo scambio termico.
Se si considera un conduttore elettrico che dissipa calore per effetto Joule, e in cui si possono raggiungere temperature eccessivamente elevate, questo risultato può essere favorevole. In questo caso, infatti, si vuole che lo scambio termico sia il maggiore possibile, e quindi si riveste il filo di una guaina elettricamente isolante di spessore pari al raggio critico, meno il raggio del cavo elettrico. Inoltre per aumentare lo scambio termico, in modo considerevole, si può aumentare la superficie di scambio, utilizzando un filo di sezione maggiore.
A questo punto determiniamo il raggio critico dell’isolante, andando a derivare rispetto a r3 la formula della potenza termica scambiata (equazione 6); in particolare quest’ultima è massima quando:
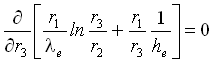 (9)
(9)
Procedendo con i calcoli:
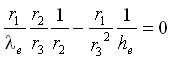 (10)
(10)
da cui posso calcolare il valore del raggio critico:
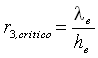 (11)
(11)
Quindi, tale valore dipende sia dalla conducibilità termica del materiale, sia dal coefficiente di convezione esterno. In particolare se il coefficiente di convezione esterno è piccolo e viceversa la conducibilità del materiale è ragionevolmente grande, il raggio critico diventa molto grande (può essere 4 o 5 volte il raggio del tubo metallico). Inoltre non basta superare il raggio critico per vedere una diminuzione della potenza termica scambiata, rispetto al caso del tubo nudo, bisogna superare un valore che è circa il doppio del raggio critico.
1.2. Cavo elettrico percorso da corrente
E’ dato un filo elettrico, teso orizzontalmente in una stanza, di sezione S pari a 1mm2 (anche se le norme dell’elettrotecnica impongono per gli impianti domestici una sezione minima di 1,5mm2 per correnti fino a 10A, o una sezione minima di 2,5mm2 per correnti fino a 16A). Tale filo ha una resistenza R, per unità di lunghezza, pari a 1W /m, ed è percorso da una corrente i pari a 5A. Si può notare come questo sia un filo di bassa qualità, in quanto un buon conduttore ha una resistenza pari a circa ¼ la resistenza del filo in considerazione.
Si deve determinare la temperatura del filo, conoscendo il valore del coefficiente di convezione esterno he, pari a 50W/m2°K. Tale valore è eccessivamente elevato, in quanto in esso è compreso anche una quota per lo scambio termico per irraggiamento.
A questo punto è necessario determinare la potenza dispersa per metro di lunghezza:
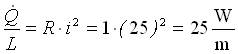 (12)
(12)
Questa potenza appena calcolata, viene dispersa per convezione, e quindi sarà uguale a:
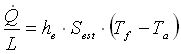 (13)
(13)
dove Tf è la temperatura del filo, e Ta è la temperatura dell’aria ambiente (che poniamo pari a 20°C).
Considerando che il filo ha una sezione S pari a 1mm2, il suo raggio rf si calcola nel seguente modo :
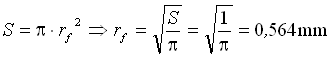 (14)
(14)
Possiamo quindi ricavare la temperatura del filo:
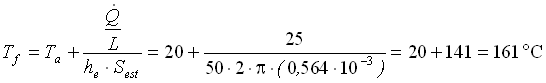 (15)
(15)
dove, come superficie Sest abbiamo considerato l’area esterna del nostro filo, cioè quella a contatto con l’aria, attraverso la quale avviene lo scambio termico.
Bisogna stare attenti a non confondere questa superficie con la sezione del filo. Infatti il moto degli elettroni avviene parallelamente al filo, mentre il calore si dissipa perpendicolarmente al filo ad al moto degli elettroni (fig.4).
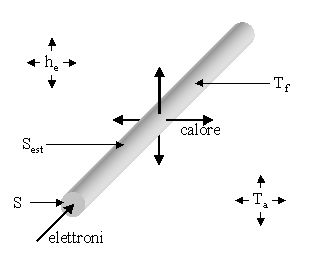
Figura 4. Filo percorso da corrente
La temperatura del filo risulta molto elevata, in quanto la superficie di scambio è molto piccola. Decidiamo perciò di mettere una guaina di gomma attorno al filo, per favorire la dispersione del calore, ed evitare che lo stesso si bruci.
Il raggio ottimale di questa guaina, sarà il raggio critico dell’isolante.
Se si utilizza un materiale con una conducibilità termica l g pari a 1W/m°K, tramite l'equazione 11, il raggio ottimale che si ottiene, è:
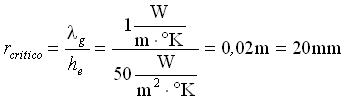 (16)
(16)
Aumentando il raggio dell’isolante fino a 20mm (che è un valore molto elevato confrontato con il raggio del filo), lo scambio termico aumenta. Si è ottenuto un valore così alto, in quanto è stato usato un materiale con un alta conducibilità.
Si calcoli come viene a modificarsi la temperatura del filo, una volta aggiunta la guaina di gomma.
Volendo fare un calcolo più accurato, bisognerebbe tenere conto che abbiamo ipotizzato che il coefficiente di convezione esterno rimanga costante a 50 W/m2°K, il che non è vero, perché in realtà con l’aumentare della superficie di scambio, he cala, e quindi il raggio critico crescerebbe.
Nell’ipotesi di coefficiente di convezione costante, la potenza termica scambiata per metro di lunghezza, utilizzando l'equazione 6, risulta:
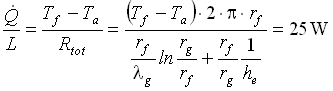 (17)
(17)
considerando due resistenza in serie:
La nostra incognita è la temperatura del filo Tf, che si può ricavare nel seguente modo:
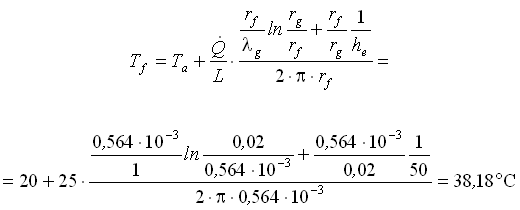 (18)
(18)
Questa temperatura è molto più accettabile rispetto ai 161°C, che si era ottenuto senza il rivestimento.
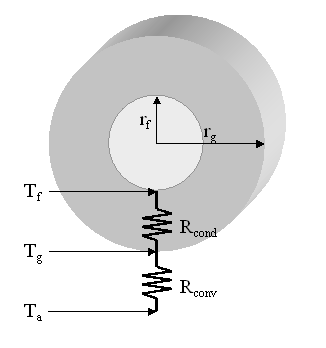
Figura 5. Rappresentazione mediante l'uso delle resistenze
Un altro parametro interessante da valutare è la temperatura di parete esterna dell’isolante Tg, calcolabile considerando il partitore di tensione dato delle due resistenze in serie. Conoscendo la potenza che fluisce, posso calcolare sulla resistenza esterna (analogamente si potrebbe fare su quella interna), la differenza di temperatura tra la temperatura della gomma e la temperatura dell’aria, utilizzando la legge di Ohm.
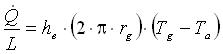 (19)
(19)
da cui si ricava la temperatura sulla gomma:
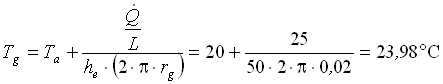 (20)
(20)
Si poteva quindi utilizzare un isolante con uno spessore minore, ottenendo ugualmente un buon risultato in termini di temperatura della gomma, avendo così un risparmio economico. Migliore ancora, sarebbe utilizzare un filo con sezione più grande o con una resistenza minore, favorendo in questo modo la dissipazione di calore.
2. Convezione naturale e convezione forzata
2.1. Convezione naturale
Supponiamo di avere una cavità chiusa di forma quadrata, in cui le pareti sopra e sotto sono adiabatiche, quindi attraverso esse non si ha luogo a nessuno scambio di calore; mentre la parete sinistra e la parete destra sono riscaldate tramite due bagni termostatici che mantengono alla temperatura T1 e T2 le due pareti. Si impone la temperatura T1 maggiore della temperatura T2.
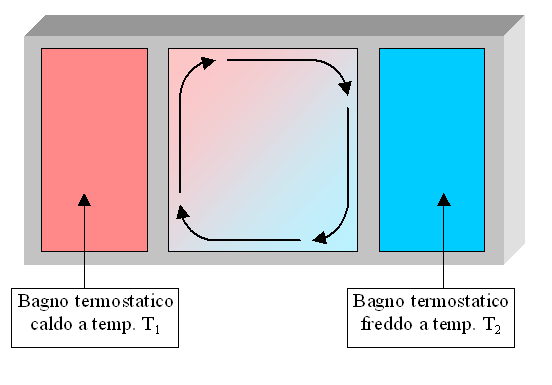
Figura 6. Fluido in moto convettivo
All’interno della cavità vi è un fluido, che si ipotizza sia acqua.
Se il fluido stesse fermo, si avrebbe pura conduzione in una lastra piana, fenomeno già trattato in lezioni precedenti.
In realtà, l’acqua a contatto con la parete calda si dilata, in quanto, come tutti i fluidi, l’acqua è dotata di un coefficiente di dilatazione termica b , definito:
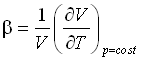 (21)
(21)
Il coefficiente di dilatazione termica b , si misura in °K-1, e normalmente è positivo, quindi con l’aumentare della temperatura, cresce il volume. Ciò è vero per i solidi, per i liquidi e per i gas.
Per un gas perfetto:
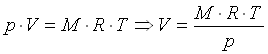 (22)
(22)
di conseguenza il coefficiente di dilatazione termica risulta:
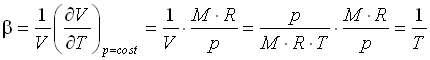 (23)
(23)
Di seguito è riportata la tabella dei coefficienti di dilatazione termica b , per alcuni fluidi.
|
Materiale |
Coefficiente di dilatazione termica b (°K-1) |
|
Acqua |
0,18 × 10-3 |
|
Alcool etilico |
1,04 × 10-3 |
|
Ammoniaca |
2,448 × 10-3 |
|
Anidride Carbonica |
14 × 10-3 |
|
Anidride Solforosa |
1,944 × 10-3 |
|
Benzina |
0,96 × 10-3 |
|
Cloroformio |
1,4 × 10-3 |
|
Diclorodifluorometano (Freon 12) |
2,628 × 10-3 |
|
Glicerina |
0,53 × 10-3 |
|
Glicol Etilenico |
0,648 × 10-3 |
|
Mercurio |
0,1818 × 10-3 |
Tabella 1. Coefficienti di dilatazione termica b
Ritornando al problema precedente, l’acqua a contatto della parete calda, essendo dotata di un b maggiore di zero, aumenta di volume e quindi diventa più "leggera" e per effetto dalla spinta di Archimede, tende a salire verso l’alto.
Viceversa dall’altra parte, l’acqua a contatto della parete fredda, cala di volume, e quindi tende a scendere verso il basso.
Tali fenomeni si verificano sul nostro pianeta per effetto della forza di gravità e non si verificano in ogni altro luogo in cui non ci sia gravità. Infatti, sono le forze di gravità, unitamente al fenomeno della dilatazione termiche che fanno sì, che si generi un moto convettivo.
Il fluido, quindi, inizia ad andare in rotazione, e così facendo, l’acqua che prima si era scaldata va a toccare la parete fredda, mentre l’acqua che si è raffreddata va a passare sulla parete calda. Così facendo, il trasporto di energia tra le due pareti è molto più veloce, rispetto al trasporto che si avrebbe per pura conduzione.
Questo fenomeno prende il nome di convezione naturale. La convezione è naturale quando il moto del fluido è causato dello scambio termico stesso, e, se lo scambio termico viene a mancare, allora anche il moto viene a cessare. Esiste una relazione di causa - effetto tra lo scambio termico e il moto del fluido.
2.2. Convezione forzata pura e convezione mista
Si suppone, ora, di avere un filo elettrico teso orizzontalmente, che dissipa calore per effetto Joule. Per evitare che diventi troppo caldo si utilizza un ventilatore che emette un flusso d’aria con velocità v¥ ortogonalmente al filo (fig.7a). Facciamo quello che si chiama un raffreddamento forzato.
In questo caso l’aria che lambisce il filo, a temperatura più calda, porta via calore della superficie del filo stesso. Il calore che si disperde è molto più elevato del calore che se ne andrebbe, per convezione naturale, se non ci fosse il ventilatore. Anche in convezione naturale, l’aria scaldata, si sarebbe messa in moto, ma con un movimento molto più lento (fig.7b).
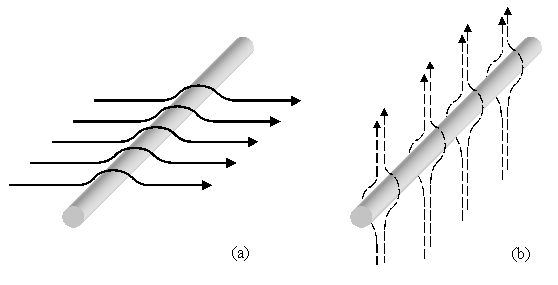
Figura 7. Filo investito da un flusso d'aria proveniente da un ventilatore (a). Filo in un cui si ha convezione naturale (b).
Quando il moto dell’aria è forzato dall’esterno, ed avviene anche se il filo è freddo, si parla di convezione forzata.
La convezione naturale non è annullata dalla presenza di convezione forzata, la quale è normalmente 10–15 volte maggiore. Questi due tipi di convezione si vanno a sommare, tenendo comunque conto della direzione e del verso del flusso d’aria. Si ha una somma di tipo vettoriale.
Esistono quindi oltre ai casi di convezione naturale e di convezione forzata, i casi di convezione mista. In particolare:
In tutti questi casi, si deve andare a calcolare il coefficiente di convezione h, utilizzando la seguente relazione:
![]() (24)
(24)
dove Tparete e Tf sono la temperatura del filo sulla superficie esterna, e la temperatura dell'aria a grande distanza dal filo.
Bisogna tenere sempre presente, che la convezione è un fenomeno che avviene nel fluido, e non nella parete. Nella convezione, infatti, si considera la temperatura di parete esterna; come si sia ricavato tale valore è un problema della conduzione nel corpo solido. Qualunque sia il materiale di cui è fatta la parete, per la convezione l’unico dato utile è la temperatura esterna.
2.3. Scambio termico coniugato
Si prenda, ora, una lastra metallica, che ha un certo spessore s e una certa altezza H. La faccia di sinistra è bagnata da un bagno termostatico e quindi su tale superficie avviene uno scambio di calore per convezione.
Essendo la convezione forzata, ed essendo il fluido acqua, il coefficiente di convezione è molto elevato. In pratica si impone alla faccia sinistra della lastra la temperatura del bagno termostatico, che fisseremo uguale a T1.
Analogamente sulla faccia destra, c’è dell’acqua, a temperatura T2, minore rispetto al bagno termostatico, che, a contatto con la parete, si scalda e risale verso l’alto.
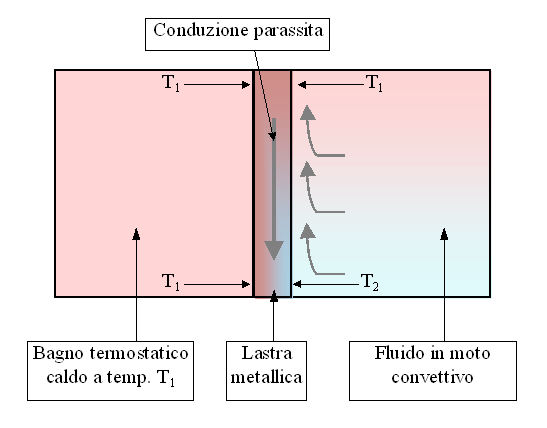
Figura 8. Esempio di scambio termico coniugato
Si ha quindi, che in basso, sulla parete destra, la lastra si trova ad una temperatura relativamente bassa, mentre in alto la sua temperatura ha quasi raggiunto la temperatura T1.
In conseguenza di ciò, il valore locale del coefficiente di scambio non è lo stesso. Nella parte bassa della lastra lo scambio sarà molto più elevato rispetto alla parte alta.
Così anche la temperatura esterna della lastra non sarà la stessa. Essendo la lastra composta da un certo materiale con una certa conducibilità , la parte superiore della lastra sarà più calda della parte inferiore.
Dal momento che dentro la lastra, che è un solido, vi è una differenza di temperatura, si innescano scambi di conduzione. Il calore quindi fluirà dalla temperatura più alta alla temperatura più basso (dall'alto verso il basso). Questo tipo di conduzione prende il nome di conduzione parassita; mentre il fenomeno visto nel suo assieme, si chiama scambio termico coniugato, in quanto si sviluppa uno scambio termico conduttivo nel metallo, causato dalla non uniformità dello scambio termico per convezione all’esterno di esso.
Essendo la convezione e la conduzione difficilmente dissociabili, la risoluzione analitica di questo problema è pressoché impossibile; per calcolare adeguatamente questi fenomeni è necessario risolverli con metodi numerici, quali possono essere il calcolo agli elementi finiti o alle differenze finite.
Nei casi che andremo a studiare eviteremo la conduzione parassita; considereremo sempre corpi isotermici, corpi con conducibilità termica talmente elevata (quale potrebbe essere il filo conduttore di rame) da poter considerare la sua temperatura costante in ogni punto. Ciò non potrebbe essere vero per una barra di grafite, che ha una conducibilità termica molto bassa, tale da non poter considerare la temperatura costante in due punti diversi della barra stessa.
2.4. Convezione a flusso di calore imposto e convezione a temperatura imposta
Si analizzano ora due esempi apparentemente simili, ma che danno luogo a due risultati diversi.
Nel 1° caso, si ha dell’acqua che scorre in un tubo, il quale è riscaldato elettricamente. Vi è una certa corrente elettrica che passa dentro il metallo stesso del tubo, e così facendo si ha dispersione di calore per effetto Joule. In questo modo si impone in ogni punto del condotto, un flusso di calore imposto, per unità di superficie, ![]() , pressoché uniforme.
, pressoché uniforme.
Il fluido che scorre all’interno del tubo, sarà soggetto ad una condizione al contorno di tipo convettivo di flusso imposto.
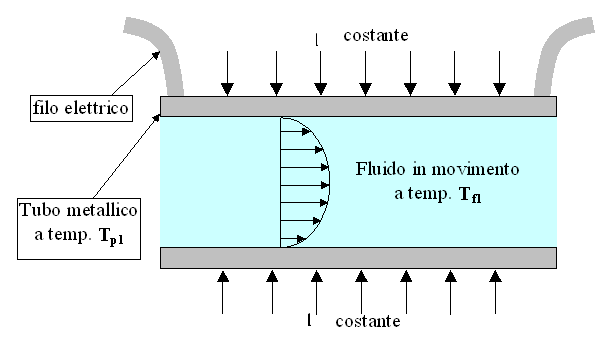
Figura 9. Esempio di convezione a flusso di calore imposto
Nel 2° caso, si ha lo stesso tubo di prima, posto all’interno di una particolare struttura, in cui si fa condensare del vapore d’acqua a pressione atmosferica, quindi a temperatura Tp2 pari a 100°C. In questo modo si riesce a mantenere costante la temperatura di parete esterna del tubo metallico.
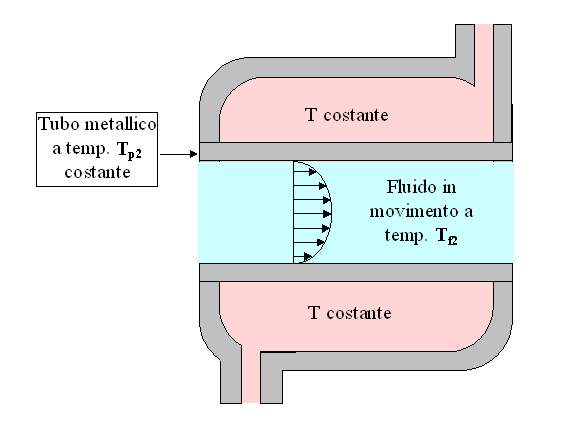
Figura 10. Esempio di convezione a temperatura imposta
Supponendo di far circolare dell’acqua, con lo stesso profilo di velocità che si aveva nel 1° esempio, il coefficiente di convezione che si sviluppa all’interno del tubo è diverso nei due casi che si sono considerato.
Il moto del fluido è esattamente lo stesso, ma la distribuzione di temperatura del fluido stesso, lungo il tubo, è diversa.
Nel secondo esempio, il fluido scambia calore con una parete che rimane costante a 100°C, per cui all’inizio lo scambio termico è molto intenso, e con il proseguire del fluido all’interno del tubo, la scambio si riduce, in quanto il fluido si scalda. Infatti, con l’avanzare del fluido, la sua temperatura Tf2 tende asintoticamente alla temperatura di parete.
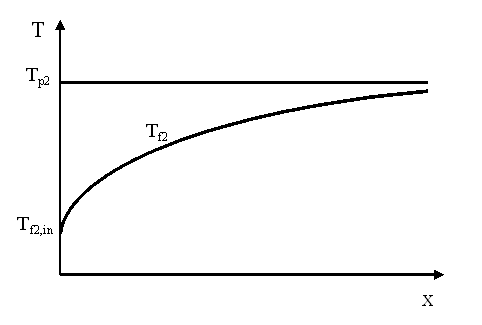
Figura 11. Temperatura di parete Tp2 e temperatura del fluido Tf2 in funzione della coordinata x, per la convezione a temperatura imposta
Nel primo esempio, invece, in cui si ha un flusso di calore imposto, la temperatura del fluido Tf1 cresce in modo lineare; mentre la temperatura di parete Tp1 tende a stabilizzarsi ad un valore:
![]() (25)
(25)
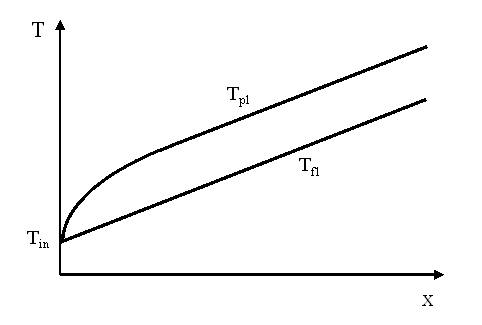
Figura 12. Temperatura di parete Tp1 e temperatura del fluido Tf1 in funzione della coordinata x, per la convezione a flusso di calore imposto
Il fatto che la temperatura del fluido cresca in modo lineare, può essere ricavato partendo dal bilancio dell’entalpia di un sistema aperto tra la sezione di ingresso e la sezione ad una certa distanza x dall’inizio del tubo :
![]() (26)
(26)
in cui ![]() è la portata in massa di fluido, Tin è la temperatura del fluido all’inizio del tubo, Tx la temperatura del fluido alla coordinata x. In particolare la potenza termica scambiata è uguale a:
è la portata in massa di fluido, Tin è la temperatura del fluido all’inizio del tubo, Tx la temperatura del fluido alla coordinata x. In particolare la potenza termica scambiata è uguale a:
![]() (27)
(27)
Quindi al crescere di x, cresce in modo lineare la potenza, e cresce, sempre in modo lineare, Tx.
Per la convezione a flusso di calore imposto, la differenza di temperatura tra fluido e parete, a parte una certa regione iniziale, tende a diventare costante; mentre per la convezione a temperatura imposta, la differenza di temperatura tende ad andare a zero.
Per entrambi gli esempi considerati si ha convezione forzata, stesso regime di moto del fluido, stesso fluido, tubo e geometria uguali; ma variano le condizioni al contorno termico. Il coefficiente di convezione, che si ha nei due casi, è diverso.
Si può, inoltre, notare che il coefficiente di convezione, varia nello spazio, e cioè con il proseguire del fluido all'interno del tubo. Nel caso di convezione a temperatura imposta, il coefficiente di convezione è massimo all'ingresso, così come è massima la differenza di temperatura, dopodiché diminuisce fino a raggiungere un valore asintotico costante.
Anche nel caso di convezione a flusso imposta, si raggiunge un valore del coefficiente di convezione costante; in ogni caso però i due valori ricavati sono diversi.
2.5. Tiraggio dei camini
Si consideri un camino non perfettamente isolato dal punto di vista termico, la cui canna fumaria, di altezza H pari a 10m, non ha nessun isolante attorno. Il fumo che scorre all'interno di questo camino, perde calore verso l'esterno, e quindi la temperatura dei fumi Tout in uscita è più bassa della temperatura dei fumi Tin all'ingresso.
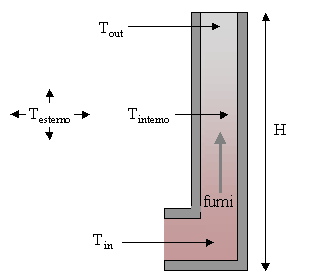
Figura 13. Canna fumaria, entro la quale si raffreddano i fumi
Partendo dal bilancio dell’entalpia di un sistema aperto tra la sezione di ingresso e la sezione di uscita:
![]() (28)
(28)
dove ![]() è la portata in massa dei fumi.
è la portata in massa dei fumi.
Allo stesso modo, questa stessa potenza termica, si può calcolare con le relazioni dello scambio termico, e quindi:
![]() (29)
(29)
dove K è il coefficiente globale di scambio, Tinterna è la temperatura all'interno del tubo (che si impone pari alla media tra Tin e Tout), e Testerno è la temperatura all'esterno.
Questo è un caso di convezione forzata. Per quanto si è visto, la convezione sarebbe naturale se, fermando lo scambio termico si fermasse il fumo. Ma annullando lo scambio termico, il fumo procede ancora più velocemente.
Per limitare la dispersione termica, si potrebbe avvolgere la canna fumaria di materiale isolante, in modo tale che i fumi restino caldi per tutto il tubo. Infatti la riduzione di temperatura dei fumi, è dannosa per il tiraggio dei camini, in quanto i fumi crescendo di densità, hanno più difficoltà ad uscire dalla canna fumaria. Il tiraggio può addirittura venire compromesso della scambio termico attraverso le pareti del tubo.