Vengono fornite qui di seguito le definizioni delle principali grandezze che giocano un ruolo fondamentale nel campo dell’acustica.

È una forma di trasporto di energia meccanica che avviene senza trasporto di materia, attraverso onde che si propagano in un mezzo elastico. La peculiarità di tale fenomeno è appunto quella di richiedere un mezzo per la sua propagazione a differenza di altri fenomeni fisici che possono farne a meno, quale ad esempio l’irraggiamento. Particolarmente interessante in questo senso è l’esperimento rappresentato qui di seguito in Fig.1.

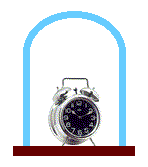
Fig.1 - Esperimento

Una sveglia posta sotto una campana di vetro in cui viene fatto il vuoto viene fatta suonare, ma all’interno della campana il suono non è udibile proprio perché l’assenza di un mezzo, in questo caso l’aria, ne impedisce la propagazione.

Il tempo riveste nell’acustica una notevole importanza al contrario di altre forme di energia quali ad esempio la luce e la corrente elettrica che, per la loro elevata velocità, possono considerare trascurabile la scala dei tempi nello sviluppo dei fenomeni a loro legati. Il suono invece dipende fortemente dal tempo in quanto la sua velocità di propagazione non è molto elevata e in ogni caso non paragonabile a quelle delle forme energetiche precedentemente elencate.

È l’energia emessa da una sorgente sonora nell’unità di tempo. La potenza sonora è il parametro indicativo di quanto una sorgente sia forte, per questo viene utilizzata come valore di riferimento nella determinazione della validità degli apparecchi acustici, come ad esempio gli altoparlanti degli impianti stereo. Attraverso la potenza acustica è possibile definire anche il rendimento sonoro di un apparecchio acustico tramite la seguente formula:

dove P_EL indica la potenza elettrica dell'apparecchio in considerazione.

È una grandezza energetica, si misura in [W/m²] e rappresenta l'energia che nell'unità tempo fluisce attraverso una determinata superficie.

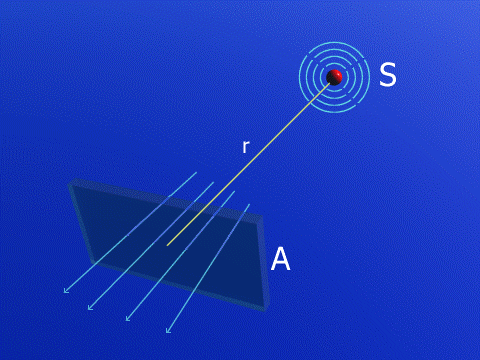
Fig.2 - Intensità di una sorgente sonora attraverso una superficie

La sorgente S di Fig.2 è puntiforme e unidirezionale, ciò significa che è piccola rispetto a r, cioè la distanza dalla superficie A, e che trasmette onde sonore in tutte le direzioni. Supponiamo quindi che la superficie misuri esattamente 1 m² e che la sorgente si trovi in campo libero, senza riflessioni e senza interferenze con il suolo o con altri corpi; sotto queste ipotesi possiamo andare a calcolare l'intensità sonora con la seguente formula

che ci permette di comprendere come l'intensità sonora di una sorgente non sia costante ma vari a seconda della distanza da quest'ultima, in virtù della dipendenza da r.

Nella definizione della velocità del suono è necessario distinguere tra velocità dell'onda e velocità delle particelle, per fare questo ci avvaliamo dell'esperimento riprodotto qui di seguito in Fig.3.

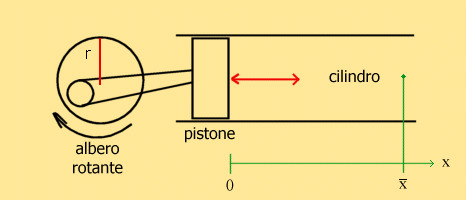
Fig.3 - Esperimento dell'albero rotante che muove il pistone all'interno del cilindro

Un albero rotante che si muove con velocità angolare w, viene collegato ad un pistone libero di muoversi all'interno di un cilindro pieno di aria; il moto del pistone sarà quindi di tipo armonico con oscillazioni di ampiezza sinusoidale date dalla seguente legge:

A(t) = r · cos(wt)

dove r indica il raggio dell'albero rotante.

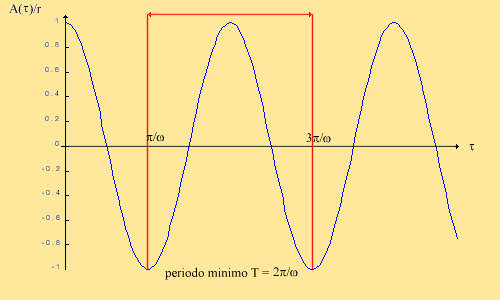
Fig.4 - Grafico delle oscillazioni in dipendenza dal tempo

Le particelle d'aria più prossime al pistone, per ipotesi di aderenza, seguono il moto di quest'ultimo per cui la loro velocità può essere ricavata derivando la legge precedentemente vista per l'ampiezza delle oscillazioni del pistone

u(t) = - wr · sen(wt)

La velocità delle particelle è quindi di tipo sinusoidale con valor medio nullo, il che significa che le particelle più vicine al pistone si muovono avanti e indietro nel tubo rimanendo aderenti al pistone. Dal momento che ogni particella è dotata di una massa e di una elasticità, la possiamo considerare come una molla infinitesima che una volta spinta dal pistone trasmette il moto a sua volta alla particella che si trova al suo fianco. Lo strato di particelle aderenti al pistone agisce elasticamente trasmettendo la spinta al secondo strato dopo un certo istante di tempo, quindi l'energia meccanica, ovvero l'onda sonora, non si propaga a velocità infinita ma con una certa velocità indicata dal simbolo c che rappresenta la velocità del suono.

La velocità della generica particella presente nel tubo in corrispondenza dell'ascissa x è ricavabile tramite una traslazione nel tempo della legge vista in precedenza

u(t,x) = - wr · sen[ w( t - t₀ ) ]

dove t₀ indica il tempo di ritardo dell'onda sulla particella alla generica ascissa x

La velocità c non dipende dalla particolare perturbazione ( forma d'onda ) né dalla sua ampiezza o dalla sua frequenza, ma dipende solo dalle proprietà termodinamiche del mezzo in cui tale perturbazione si propaga, in particolare per i gas perfetti la velocità del suono è funzione della sola temperatura, quindi

Se il mezzo è aria si ha

T = 20°C ® c @ 343 m/s

La voce di una persona che parlasse dal fondo di un'aula lunga 17 m si udrebbe all'altro capo della stanza dopo un ritardo di

t = 17 / 343 @ 0,04956 s

In realtà il valore qui sopra ricavato si riferisce al ritardo della sola onda sonora diretta e non a quello degli innumerevoli effetti di riflessione e riverberazione presenti negli ambienti chiusi, che in generale possiedono un ritardo maggiore rispetto all'onda diretta. La voce della persona arriverebbe quindi all'orecchio dell'ascoltatore con una sorta di coda sonora derivante dalla somma degli effetti già citati.

È interessante valutare quanta parte di tubo viene attraversata dall'onda sonora durante una completa oscillazione del pistone; questo valore si indica con il simbolo l, viene definito lunghezza d'onda ed è valido solo quando la legge del moto è di tipo sinusoidale

l = c · T = 2pc / w

dove T è il periodo minimo di oscillazione, detto anche lunghezza d'onda nel tempo, e w è la velocità angolare o pulsazione e si misura in [giri/s]. La pulsazione è legata alla frequenza f delle oscillazioni dalla seguente relazione

e quindi essendo

si ha che la frequenza è l'inverso del periodo minimo

La frequenza si misura in [Hz] (Hertz).

Riassumendo possiamo affermare che la principale distinzione tra velocità delle particelle e velocità dell'onda è il fatto che la prima è figlia della legge del moto imposto al pistone, mentre la seconda è invariante a parità di mezzo e di proprietà termodinamiche del mezzo stesso.

Questa proprietà del suono è fondamentale in natura; se infatti il suono non fosse costante a tutte le frequenze il sistema uditivo umano si sarebbe dovuto sviluppare in maniera completamente diversa da quello attuale per comprendere i suoni alti e i suoni bassi che viaggerebbero a velocità diverse.

La proprietà d'invarianza della velocità della perturbazione non si verifica in tutti i fenomeni fisici; esistono infatti altri fenomeni di trasporto dell'energia meccanica attraverso un mezzo, che non possiedono velocità costante, come ad esempio la propagazione delle onde marine, che è un fenomeno altamente dispersivo. Questo avviene perché la propagazione della perturbazione nelle onde marine è ortogonale alla direzione di movimento delle particelle del mare, al contrario la propagazione dell'onda sonora viaggia con onde longitudinali, cioè onde che possiedono la stessa direzione del movimento delle particelle del mezzo.

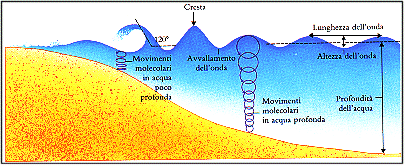
Fig.5 - Onde marine di tipo trasversali

I terremoti sono fenomeni composti da una frazione di energia che si propaga in modo longitudinale e di un'altra che invece si propaga attraverso onde trasversali; questi due treni d'onda viaggiano a velocità diverse. Le onde longitudinali sono più veloci e meno dispersive, per cui costituiscono le cosiddette scosse di avvertimento, mentre le onde trasversali arrivano con una frazione di ritardo rispetto alle precedenti e, poiché altamente dispersive, costituiscono le scosse più violente e devastanti.

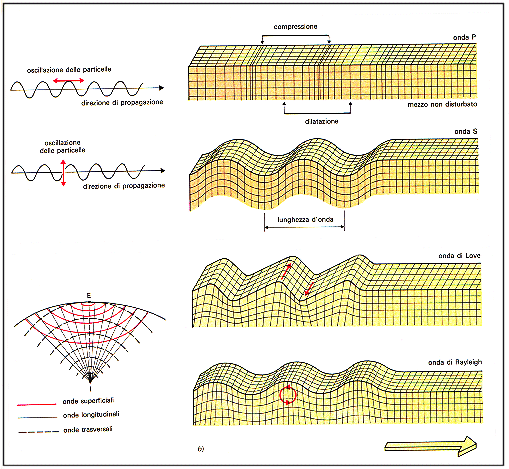
Fig.6 - Differenze tra onde trasversali e onde longitudinali nei fenomeni sismici

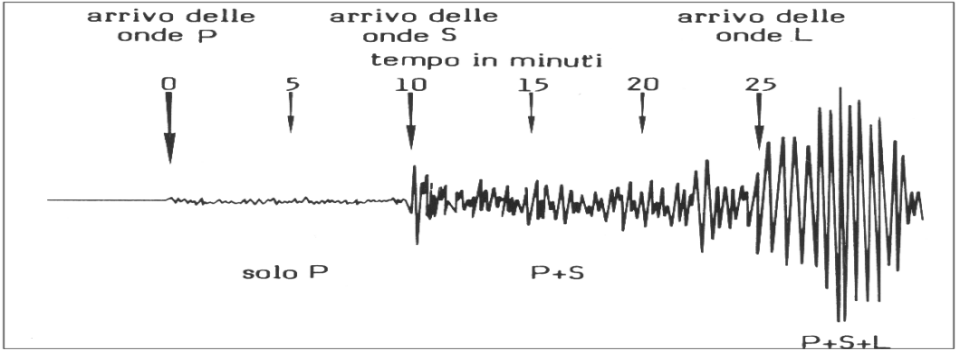
Fig. 7 - Differenza di velocità tra onde longitudinali e onde trasversali nei

terremoti

Abbiamo precedentemente detto che affinchè il suono possa diffondersi, il mezzo attraverso cui viaggiano le onde sonore deve essere elastico. Ritornando al caso del pistone mobile, possiamo dire che, dal momento che l'aria è un mezzo elastico, la sua compressione, dovuta all'avanzata del pistone, viaggia con velocità finita e quindi, ad un determinato istante di tempo e ad una opportuna distanza dal pistone, esisterà sempre uno strato di particelle rimaste ferme che costituisce una barriera all'avanzamento delle particelle perturbate dal moto del pistone. Si ha il cosiddetto fenomeno di confinamento inerziale il quale fa sì che, sebbene non vi sia una parete solida, il volume del gas diminuisca e che di conseguenza aumenti la pressione. Quando il pistone torna indietro, il volume e la pressione ritornano ai loro valori originari; possiamo quindi affermare che anche la pressione segue il moto del pistone fluttuando nel tempo con legge sinusoidale, come riportato in Fig.8.

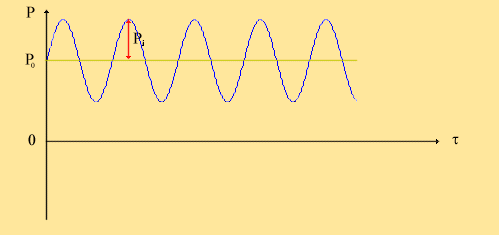
Fig.8 - Legge sinusoidale per la pressione acustica

Con il simbolo p_i è indicata la pressione istantanea, cioè la differenza tra la pressione p del gas a quel determinato istante di tempo e la pressione atmosferica media p₀

Poiché si tratta di una grandezza relativa, cioè calcolata a partire da un valore di riferimento costante, che in questo caso è la pressione atmosferica media, può assumere anche valori negativi.

Si ha il fenomeno dell'onda piana progressiva quando velocità e pressione sono in fase tra loro. Il trasferimento di energia è tanto migliore quanto più velocità e pressione sono in fase tra loro, per questo nel caso particolare in cui queste due grandezze siano sfasate di 90° si ha un trasferimento di energia nullo e non c'è propagazione del suono.

Si indica più brevemente con il simbolo RMS (dall'inglese Root Mean Square ) ed è definita dalla seguente formula

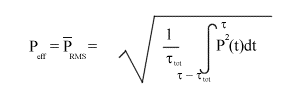
dove t_tot è l'intervallo d'integrazione sull'asse dei tempi. Questa formula ci consente di calcolare la potenza efficace considerando un'intera finestra d'integrazione per la media efficace. La risposta del mediatore viene approssimata nella realtà tramite un circuito di tipo RC, come quello schematizzato qui di seguito in Fig.9.

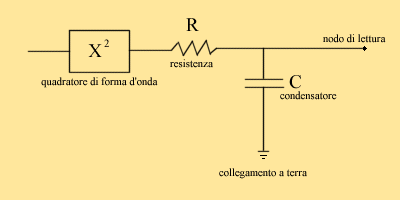
Fig.9 - Circuito RC con quadratore

Per il circuito RC la media nel tempo non è a finestra lineare, ma di tipo esponenziale, infatti

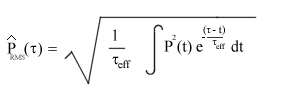
Il termine esponenziale è dotato della costante di tempo

t_eff = R · C

La risposta che si può leggere al nodo di lettura del circuito schematizzato in precedenza, ha, in teoria, memoria infinita dal momento che la finestra d'integrazione è un intervallo di lunghezza infinita, sebbene la media corrisponda ad una media in cui i valori di P precedenti hanno sempre meno rilevanza, mano a mano che ci si allontana nel passato. Esistono due valori della costante di tempo t_eff particolarmente importanti

SLOW ® RC = 1 s

FAST ® RC = 0,125 s

la risposta umana al segnale sonoro è infatti sostanzialmente simile a quella di un circuito RC con costante di tempo di tipo FAST.

L'approssimazione tramite il circuito schematizzato in Fig.9, fu fatta al tempo in cui non esistevano ancora i circuiti digitali, per questo, essendo di facile implementazione con circuiti analogici, era preferita alla media di tipo lineare. Con l'introduzione delle nuove tecnologie digitali, che implementano facilmente quest'ultimo tipo di media, si è stabilito, tramite normative internazionali, che gli strumenti di misura nel campo dell'acustica adottino la media di tipo lineare in quanto molto più precisa di quella esponenziale.

Per comprendere meglio il concetto di pressione acustica conviene legare quest'ultima con la velocità delle particelle; per fare questo ci avvaliamo dell'equazione di Navier ricavata nella sezione relativa alla fluidodinamica. Consideriamo un cilindro pieno d'aria, in cui è libero di muoversi un pistone e supponiamo per ipotesi che le pareti del cilindro siano termicamente isolate e che di conseguenza il fenomeno sia adiabatico. Sotto queste condizioni si ha che

p · r^-g = costante = p₀ · r₀^-g

in quanto per le trasformazioni adiabatiche vale la proprietà

p · v^g = costante

e sappiamo bene che

Le costanti p₀ e r₀ indicano rispettivamente la pressione e la densità del sistema in situazione iniziale di riposo. Dalle precedenti uguaglianze possiamo ricavare che

p = p₀ · ( r / r₀ )^g

e quindi andando a derivare la legge ottenuta per la pressione in funzione della densità, si ottiene

( ¶p / ¶r ) = p₀ · g ( r^{g - 1}/ r₀^g )

e poiché, ci interessa valutare il comportamento della derivata in un intorno del punto di coordinate ( p₀ , v₀ ), dal momento che consideriamo piccole oscillazioni di pressione e di volume intorno ai valori di riposo, possiamo concludere che

r = r₀ Þ ( ¶p / ¶r ) = ( p₀ · g ) / r₀ = c²

Abbiamo quindi ricavato un'espressione in cui compare il termine relativo alla velocità del suono, andandolo ad esplicitare otteniamo

e ricordandoci l'equazione di stato dei gas perfetti, possiamo andare a scrivere la relazione finale che ci dimostra come, per i gas perfetti, la velocità dipenda unicamente dalla temperatura.

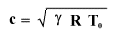
Per i liquidi la relazione che si ottiene è nella forma

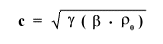
dove b è il modulo di compressibilità isoterma dato dalla seguente formula

La velocità del suono nell'acqua è di circa

un valore ben superiore a quello già visto per l'aria. Questo spiega la difficoltà, per chi si immerge nel mare, di determinare la direzione di provenienza di un suono, perché l'orecchio umano fa affidamento al tempo di ritardo con cui le due orecchie percepiscono il suono per determinarne la provenienza, ma se il suono è molto più veloce di quanto non sia nell'aria, allora qualsiasi onda sonora colpisce quasi contemporaneamente le orecchie.

Per i solidi esiste una relazione ancora differente

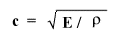
dove E rappresenta il modulo elastico del solido e si misura in [N/m²].

Nella seguente tabella sono riportati alcuni valori di riferimento per la velocità del suono in rapporto al differente mezzo di propagazione.

I differenti valori di velocità per l'azoto ci rivelano che questo tipo di gas non può essere considerato perfetto, perché se così fosse la velocità non dovrebbe variare con la pressione.