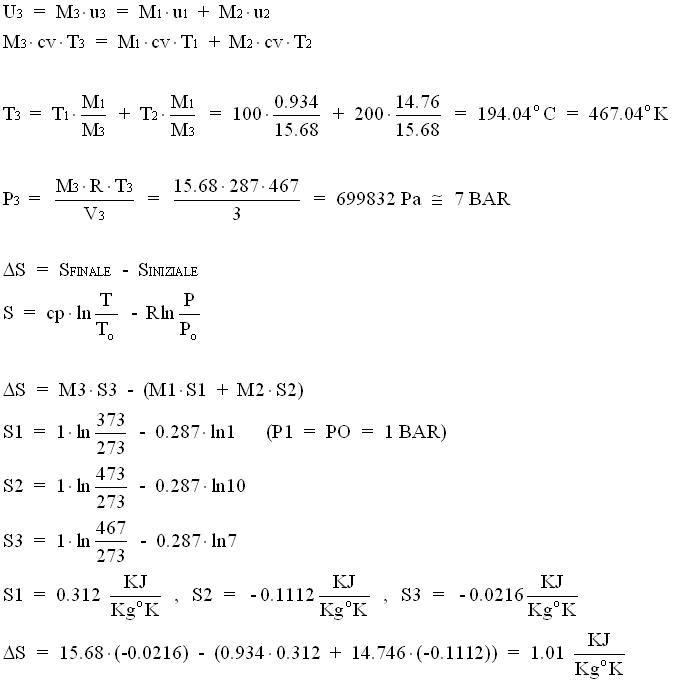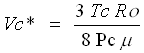 ( m
= massa molare )
( m
= massa molare )LEZIONE DEL 19/10/98 ORE 16:30 - 18:30 ENRICO COZZANI MATR. 112694
GAS REALI
EQUAZIONE DI STATO DEI GAS REALI
PV = zRT ( Dove z = PV = FATTORE DI COMPRESSIBILITA' )
RT
Si noti che, se z = 1, si ottiene l' equazione di stato dei gas perfetti.
Occorre quindi trovare un modo per determinare z in qualunque diagramma PV.
A questo scopo si introduce la cosiddetta:
LEGGE DEGLI STATI CORRISPONDENTI (Stabilisce la deviazione dal gas perfetto di tutti i gas)
"Tutti i gas hanno lo stesso scostamento z dal gas perfetto a parita' di coordinate termodinamiche ridotte"
Cosa sono le coordinate termodinamiche ridotte? (Es. Pressione ridotta , Temperatura ridotta....)
Pr = P = Pressione ridotta ( P = Pressione del gas , Pc = Pressione del punto critico)
Pc
Tr = T = Temperatura ridotta ( T = Temperatura del gas , Tc = Temperatura del punto critico)
Tc
( Il volume specifico ridotto Vr risulta univocamente determinato note Tr e Pr ).
TABELLA DI ALCUNI VALORI CRITICI
|
Pc (BAR) |
Tc (° K) |
VmC |
Zc |
|
|
ARIA |
37.3 |
132.8 |
0.083 |
0.284 |
|
OSSIGENO |
50.7 |
154.4 |
0.074 |
0.29 |
|
AZOTO |
33.9 |
126.1 |
0.09 |
0.291 |
|
ACQUA |
22.1 |
647.3 |
0.057 |
0.23 |
|
METANO |
46.4 |
191.1 |
0.099 |
0.29 |
|
AMMONIACA |
112.7 |
405.6 |
0.072 |
0.242 |
Come si vede dalla tabella , zc e' sempre attorno a 0.27¸ 0.28 , ed e' per questo motivo che alla legge degli stati corrispondenti si da' un significato solo teorico , cioe' viene per cosi' dire "presa per buona".
Dalla teoria cinetica dei gas , si e' sperimentalmente ottenuto che zc = 0.375 , per cui bisogna introdurre il cosiddetto:
volume critico convenzionale = Vc* , ovvero quel volume che ci sarebbe se zc fosse uguale a 0.375.
Quindi si ottiene la legge: PcVc* = zcRTc ( Affinche' sia soddisfatto zc = 0.375)
Da cui: 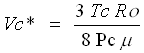 ( m
= massa molare )
( m
= massa molare )
SCOSTAMENTO ENTALPICO E SCOSTAMENTO ENTROPICO
Si puo' dimostrare che:
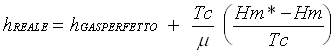 ( h = entalpia molare )
( h = entalpia molare ) 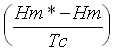 =
= ![]() scostamento entalpico
scostamento entalpico 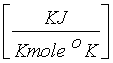 = f (Pr,Tr)
= f (Pr,Tr)
e inoltre:
![]()
![]()
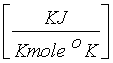 = f (Pr,Tr)
= f (Pr,Tr)
IMPORTANTE !
Cosa accade se sono poco lontano dalla curva limite ?
Esempio:
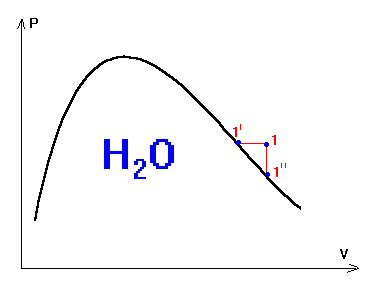
H(1) = ?
U(1) = ?
S(1) = ?
dH = dQ + VdP ,ma se P = costante Þ VdP = 0
dH = cpdT
![]()
![]()
![]()
Per l' entropia:
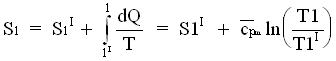
(Se T1 e' poco diverso da T1' , cioe' se 1 e' poco distante da 1' )
ESERCIZIO
scatolone adiabatico a due scomparti:
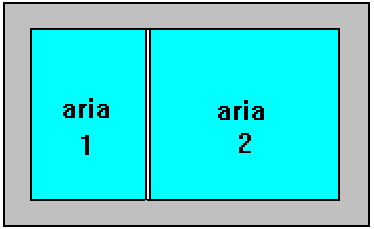
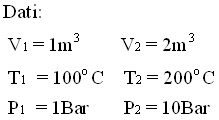
P3 = ?
T3 = ?
D S = ?
SOLUZIONE
![]()
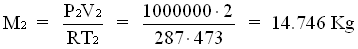
![]()
Q = 0 , L = 0 Þ dal primo principio ho che D U = 0 Þ U3 = U1 + U2