Analisi in frequenza

Analisi in frequenza
di Emanuele Baldini matr. 111896

Lezione di Fisica Tecnica del 18/01/1999 h. 10.30/12.30

ARGOMENTI:
		1 - Bande d'analisi in frequenza
		2 - Rappresentazione e calcolo degli spettri
		3 - Campionamento di un segnale
		4 - Analisi FFT
		5 - Distorsione armonica

1. BANDE D'ANALISI IN FREQUENZA

Abbiamo già definito in precedenza il concetto di spettro del suono che è una rappresentazione grafica di livello sonoro, normalmente in dB (decibel), in funzione della frequenza in Hz.
Se il suono da analizzare è un cosiddetto suono puro (segnale ad una sola frequenza costante nel tempo) per esempio una sinusoide perfetta, lo spettro del segnale avrà una singola componente alla frequenza della sinusoide, con un certo livello in dB.
Fig.1 - SPETTRO DI UNA SINUSOIDE PERFETTA DI FREQUENZA f1

In realtà qualsiasi segnale reale è costituito da un grande numero di componenti sinusoidali di ampiezza continuamente variabile nel tempo. Per questi segnali è improponibile un'analisi per toni puri perchè esistono sempre frazioni dell'energia del segnale che sono difficilmente rappresentabili con delle sinusoidi.
Infatti la rappresentazione di un segnale come somma di componenti armoniche sinusoidali secondo il teorema di Fourier, è valida solo per segnali stazionari, che spesso non corrispondono ai suoni reali.
Poichè di un suono reale interessa soprattutto l' aspetto energetico, normalmente l'analisi in frequenza viene fatta con uno spettro a bande di ampiezza finita:
le cosiddette bande d'analisi in frequenza
Il valore di livello di ciascuna banda è dato dalla somma energetica di tutte le componenti sinusoidali che hanno frequenze comprese negli estremi della banda f1 e f2.
Fig.2 - BANDA DI FREQUENZA DI ESTREMI f1 E f2, DI LIVELLO L E DI FREQUENZA DI CENTROBANDA fc

E' chiaro allora che per un segnale distribuito uniformemente su tutte le frequenze come per esempio il rumore, più è larga la banda e più sarà elevato il livello totale associato; è necessario quindi normalizzare le ampiezze perchè un confronto tra livelli di diverse bande abbia un senso.
Si sono normalizzate bande di ampiezza percentuale costante cioè bande nelle quali è costante il rapporto tra ampiezza di banda e frequenza di centro banda.
(1.1)
Le bande d'analisi base sono dette bande d'ottava che equivalgono a raddoppi di frequenza sulla scala delle frequenze.

E' ovvio che:
		- Ogni ottava è contigua
		- Ogni frequenza f₂ = 2 f₁
		- Ogni frequenza di centro banda è doppia della fc precedente

ESEMPIO 1:
una banda d'ottava ha fc = 1KHz allora:
fc successiva = 2KHz e:
(1.2)
(1.3)
Bastano 10 bande d'ottava per coprire interamente lo spettro udibile (20Hz ÷ 20KHz) infatti partendo dalla fc = 1KHz la tabella ottenuta è:

n. banda	fc [Hz]
1	31,5	Prima banda che copre con la frequenza inferiore i 20 Hz Ultima banda che copre con la frequenza superiore i 20 KHz
2	63
3	125
4	250
5	500
6	1000
7	2000
8	4000
9	8000
10	16000

Spesso occorre un'informazione più dettagliata dello spettro del suono ed è necessario quindi avere a disposizione un numero di bande superiore a 10.
Per esempio in musica per ogni ottava ci sono 12 sottoparti = NOTE. Si definiscono allora delle bande frazioni d'ottava come 1/3,1/6 o 1/12 d'ottava.

ESEMPIO 2:
Vediamo la larghezza di una banda 1/3 ottava prendendo come ottava quella fc = 1KHz

Fig.3 - BANDA PRINCIPALE SUDDIVISA IN 3 SOTTOBANDE

Banda principale:

f1	= 707 Hz
f2	= 1414 Hz
fc	= 1000 Hz

Se chiamiamo (1.4) allora
(1.5) quindi
(1.6)
(1.7)

OSSERVAZIONE:

si nota che la divisone in 3 sottobande genera una sottobanda avente ancora f c = 1KHz. Questa è la caratteristica di cui gode solamente la suddivisione in 1/3 d'ottava.

E' quindi chiaro che parlare di un limite per un livello non ha senso perchè quel determinato livello può essere relativo ad una banda larga 1 Hz come ad una banda larga 707 Hz.
E' sempre importante confrontare limiti di livello a larghezza di banda assegnata.

2. RAPPRESENTAZIONE GRAFICA DELLO SPETTRO DI RUMORE

Fig.4 - SPETTRO DI RUMORE IN SCALA LINEARE DALLA ANALISI IN AMPIEZZA DI BANDA PERCENTUALE COSTANTE

Fig.5 - SPETTRO DELLO STESSO RUMORE IN SCALA LOGARITMICA

Fig.6 - STESSO RUMORE IN SCALA LINEARE DALLA ANALISI IN BANDA STRETTA

Fig.7 - STESSO RUMORE IN SCALA LOGARITMICA

OSSERVAZIONE:

Confrontando il livello di rumore ad una determinata freuenza in fig.4 e in fig.6, in quest'ultima il livello è minore pur essendo alla stessa frequenza di fig.4; questo perchè l' ampiezza delle bande in fig.4 e in fig.5 è più grande di quella di fig.6 e fig.7.

3. CAMPIONAMENTO DI UN SEGNALE

In passato l'analisi veniva fatta con filtri analogici la cui curva di risposta nel dominio della frequenza approssimava lo spettro delle odierne bande con curve gaussiane.
L' apparecchio usato era il fonometro analogico che analizzava una sola frequenza alla volta. Oggi l'utilizzo pratico della teoria sulla Trasformata di Fourier permette di passare dal dominio analogico al dominio digitale.

Fig.8 - CAMPIONAMENTO DI UN SEGNALE ANALOGICO AD INTERVALLI REGOLARI DI TEMPO

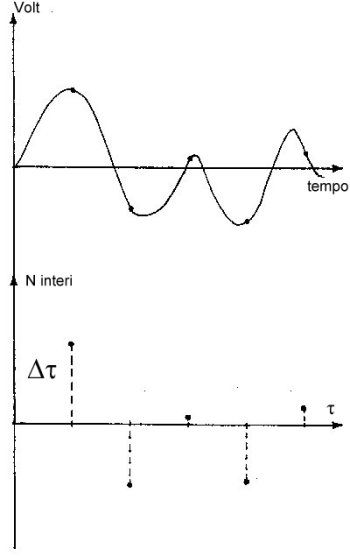
Il segnale analogico viene campionato ad intervalli temporali prefissati e non si ha alcuna informazione sul valore del segnale tra ciascun istante di campionamento.
Il tempo è espresso come (3.1)
con = intervallo di campionamento
t = indice di tempo (numero intero)

Più è breve l'intervallo di campionamento e più il segnale campionato approssima il segnale reale; questo provoca però un aumento del volume di dati da gestire.
Questo processo è svolto da un convertitore analogico/digitale

Segnale analogico

Segnale digitale

OSSERVAZIONE:

il convertitore A/D ha una precisone finita e fornisce in ogni uscita dei numeri interi con segno (signed-integer) che costituiscono i valori d'ampiezza del segnale d'ingresso discretizzato.

Un A/D a 16 BIT fornisce ą32767 valori di livello con una tecnologia che permette una frequenza di campionamento

(3.2)

Oggi si raggiungono frequenze di 96 KHz con 24 BIT formali.

OSSERVAZIONE:

ogni BIT aggiunto provoca un raddoppio del numero di valori del campo dinamico

APPLICAZIONI PRATICHE:

Elettroacustica:	il cui scopo ultimo è di riprodurre il segnale dopo averlo processato
Metrologia-acustica:	il cui scopo è di convertire il segnale in un certo dominio numerico con l'accorgimento che l'errore nei valori finali sia compatibile con le incertezze tollerabili delle misure fatte

TEOREMA DI NYQUIST

Enunciato:

La frequenza di campionamento di un segnale deve sempre essere almeno doppia della massima frequenza contenuta nel segnale da campionare

(3.3)

Definzione:

(3.4)

Il significato fisico di questo limite inferiore è dovuto al fatto di perdere informazioni contenute nel segnale se lo si campiona a frequenze troppo basse.

EFFETTO ALIASING

Se si campiona il segnale ad una freuenza inferiore a questo limite (sottocampionamento), nello spettro compaiono delle componenti "fantasma" a valori di frequenze speculari a quelle tagliate dalla f_{NYQUIST. Queste componenti "fantasma" non esistono nel segnale originale e vanno così a falsare i valori delle componenti spettrali del segnale campionato:

fALIASING = fNYQ. - (fOUT - fNYQ.). (3.5)

Fig. 10 - EFFETTO ALIASING SU UN SEGNALE DI DIVERSE ARMONICHE}

	_{= ARMONICHE INTRODOTTE NEL CAMPIONAMENTO}
	_{= ARMONICHE REALI DEL SEGNALE}

_{Per risolvere il problema Aliasing senza aumentare la fCAMPION., si interpone al convertitore A/D un filtro passa-basso anti-Aliasing che attenua fortemente tutte le componenti di segnale a frequenze superiori alla fNYQUIST.

Fig.11 - SCHEMA A BLOCCHI DISPOSITIVO ANTI-ALIASING}

_{Segnale analogico}

_{Segnale campionato}

_{4. ANALISI FFT (FOURIER)

Abbiamo visto come ottenere dei dati campionati da un segnale, in particolare pensiamo ad una sequenza di dati (vettore), memorizzati da un calcolatore: per ricavare lo spettro si prendono N dati e si elaborano con un algoritmo FFT che rende N/2 numeri complessi che rappresentano ognuno modulo e fase di una componente sinusoidale di una certa frequenza del segnale campionato.

Fig.12 - RAPPRESENTAZIONE SCHEMATICA DI UN PROCESSO FFT}

_N.campioni	_n.reali	_n.immagin.
₁	₁	_-
₂	₂	_...
₃	₃	_...
₄	_. .	_. .
_. . N	_{N/2 +1}	_-
_{Locazioni di memoria}	_{Locazioni di memoria}

_{Ad ogni numero complesso è associata la propria frequenza ed in particolare (4.1)

T = Periodo di analisi}

_{f0 = 0 Hz}

f2 = 2 f1 (4.2)

f3 = 3 f1

_{che sono le frequenze di centro banda di centro banda nello spettro in banda stretta}

_{OSSERVAZIONE:}

_{Il primo numero memorizzato relativo alla frequenza di 0 Hz corrisponde alla componente continua del segnale (solo parte reale).

Allora f1 è detta risoluzione in freq..

L'ultimo numero memorizzato (anch'esso a sola parte reale) appartiene invece alla componente armonica della freq. di Nyquist.}

_{Poichè costituiti da parte reale e immaginaria, i dati in uscita dall'FFT vengono sovrascritti nelle locazioni di memoria che contenevano gli N dati all'ingresso. Così facendo si sostituisce ad una rappresentazione del segnale nel tempo, una rappresentazione fatta nel dominio della frequenza con tanti spettri relativi ai blocchi di N dati processati ogni volta che pure si susseguono nel tempo. Si ottiene allora una sequenza nel tempo di spettri dello stesso segnale che graficamente sono rappresentati da un sonogramma.

SONOGRAMMA DI UN SEGNALE VARIABILE NEL TEMPO

La teoria dell'analisi di Fourier ipotizza però che il segnale sia periodico (N campioni che si ripetano periodicamente). Non si ha spesso a che fare con segnali periodici che hanno spettri distinti.

Fig.14 - SPETTRO REALE E IDEALE DI UNA SINUSOIDE

Questo sparpagliamento di energia dalla banda centrale alle bande laterali è detto fenomeno Leaking. Si rimedia a questo problema forzando a zero il segnale al di fuori di una finestra normalizzata di frequenza caratteristica (Hamming).

Fig. 15 - SEGNALE SINUSOIDALE LIMITATO AL DI FUORI DELLA FINESTRA

Fig.16 - SPETTRI DI SINUSOIDE CON DIVERSI TIPI DI FINESTRE APPLICATE

Applicando queste finestre di frequenza all'analisi consecutiva di N campioni, si shiftano di N/2 campioni le finestre di analisi in modo da mantenere mediamente costante il peso di ogni campione all' interno di finestre consecutive.

Fig.17 - ANDAMENTO NEL TEMPO DEL FATTORE DI PESO PER Ncampioni

La lunghezza di shift dipende però dalla finestra usata (N/2 per la Hamming).

Questo metodo richiede però un aumento del volume di dati da memorizzare nel processo di analisi.

5. DISTORSIONE ARMONICA

Aumentando il livello del segnale, è possibile che il convertitore non riesca ad avere un campo dinamico sufficiente a contenere la escursione del segnale. Questo provoca la cosiddetta distorsione armonica: la forma d'onda campionata è "tagliata" sui picchi del convertitore, che la vede così arricchita di componenti armoniche ad altre frequenze estranee al segnale originale, andando così a flasare lo spettro.

Fig.18 - SEGNALE SINUSOIDALE TAGLIATO SUI VALORI MASSIMI}