Università degli studi di Parma
Autore : Azzali Andrea
Matricola : 112687
Relazione del 22/12/98
Ora 8.30 -- 10.30
SCAMBIATORI DI CALORE
Gli scambiatori di calore sono sistemi aperti che vengono utilizzati per scambiare calore fra due fluidi a diversa temperatura. Lo scambio termico tra i due fluidi avviene solitamente attraverso una parete metallica che separa gli stessi.

Figura 1 Schematizzazione di uno scambiatore tubo in tubo
Ad esempio il fluido A e il fluido B raffigurati schematicamente in figura non vengono a contatto e quindi non si mescolano. Questo tipo di scambio avviene fra aria ed acqua nei radiatori dei motori a scoppio oppure nel processo di pastorizzazione del latte in cui latte e vapore sono tenuti strettamente isolati per motivi igienici e per motivi di contaminazione del prodotto stesso. Esistono anche scambiatori a contatto i quali vengono usati più raramente di cui non verrà fatta alcuna trattazione. Le modalità di scambio del calore in questi dispositivi sono due :
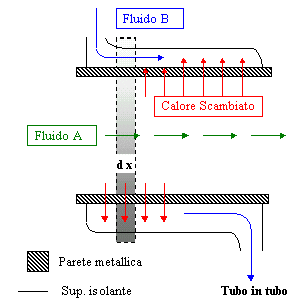
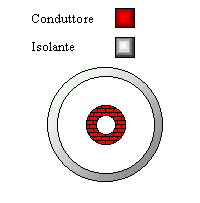
Figure 2-3. Sezioni longitudinale e normale di uno scambiatore tubo in tubo.
I tipi di scambiatori più in uso sono :
In entrambe i casi il fluidi servito entra a una temperatura T1 e viene riscaldato fino a una temperatura T2 .A comportarsi in modo diverso è invece il fluido di servizio il quale cambia il suo comportamento secondo il suo verso di scorrimento.
Questo viene evidenziato nei due grafici appresso.
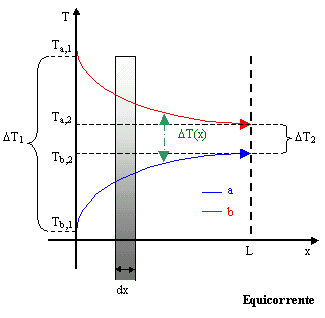
Figura 4. Grafico T(x) dello scaldatore in equicorrente.
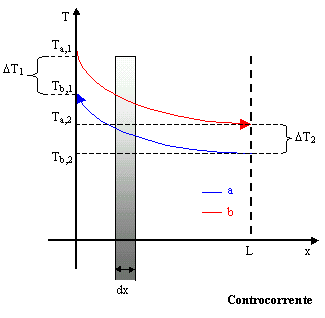
Figura 5. Grafico T(x) dello scaldatore in controcorrente.
Dai grafici messi a confronto emerge subito che :
Consideriamo ora il caso in equicorrente cercando di ottenere una espressione del calore scambiato del tipo :
![]() (1)
(1)
Mi si pone il problema di determinare quale variazione di temperatura devo considerare : D T1 , D T 2 , D T medio ?
Supponiamo di essere a pressione costante in quanto i liquidi sono in prima approssimazione incomprimibli. Dal primo principio della Energia ho :
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
A regime la quantità termica scambiata è nulla perché il calore scambiato dai due liquidi è uguale in modulo ma di segno opposto. Quindi a regime ottengo
![]() ( A REGIME ) (5)
( A REGIME ) (5)
Ora considero la sezione dx come illustrata in figura 1-2. Lungo questo tratto infinitesimo ho uno scambio di calore anch’esso infinitesimo dQi . Sviluppiamo le nostre considerazioni in primo luogo sulla superficie interna del tubo interno in cui ho scambio termico per convezione. Sappiamo che :
![]() (6)
(6)
e per la superficie interna:
![]() (7)
(7)
Ottengo :
![]() (8)
(8)
Ma la variazione di calore fra questi due punti mi da una variazione infinitesima della temperatura dei fluidi che ricavo dalla formula della capacita calorica :
![]() (9)
(9)
![]() (10)
(10)
Ora eseguo la differenza dei due termini dTA e dTB e ottengo :
In questa equazione andiamo a sostituire dQi con il valore ricavato nella formula (8) ottenendo come risultato una equazione differenziale di prim’ordine a variabili separate:
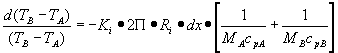 (11)
(11)
Cerco una soluzione generale al problema di Cauchy integrando l’equazione trovata :
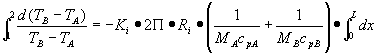 (12)
(12)
Ottengo la soluzione :
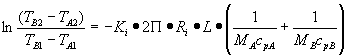 (13)
(13)
Gli scambiatori tubo in tubo lavorano in regime di scambio di convezione forzata e quindi sappiamo che il coefficiente di scambio K i è debolmente dipendente dalla temperatura. Cerchiamo allora di raggiungere una espressione esplicita di DT m e d i o . Dal sistema delle due equazioni trovate ricaviamo la nostra incognita .Sappiamo che:
![]() (14)
(14)
Andando a sostituire nella formula (13) ottengo :
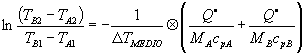 (15)
(15)
Ma dalle equazioni (2) e (3) ricavo che:
![]() (16)
(16)
Dalla risoluzione di questo sistema lineare ottengo l’espressione cercata di DT medio il quale per la sua forma particolare viene detto DT m e d i o LOGARITMICO :
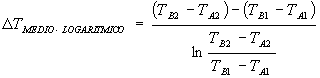 (17)
(17)
Questa espressione del DT m e d i o può essere utilizzata sia per gli scambiatori che lavorano in equicorrente sia per quelli che lavorano in controcorrente in quanto durante i calcoli non ho fatto alcuna ipotesi se non quella iniziale di essere a pressione costante. Quindi considerando i moduli delle temperature posso cambiare lo stato A in B e viceversa (A Þ B ) . Consideriamo ora alcuni esempi in cui si usano fluidi particolari.
ARIA CALDA. Ipotizziamo che i liquidi in questione siano entrambi aria calda ovvero che entrambe abbiano pari calore specifico a pressione costante. Ovvero :
![]()
Supponiamo ora che la portata del fluido A che chiamiamo MA sia doppia rispetto alla portata di B, MB restando però a sezione costante.
![]()
![]()
Il mio DT m e d i o risulta diverso nei due casi di equicorrente e controcorrente determinando un calore scambiato fra i due fluidi differente :
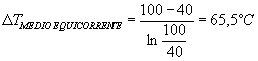
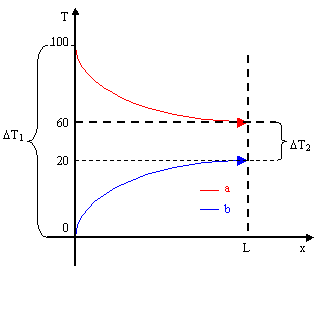
Figura 6. Diagramma T(x) in un caso particolare di scambiatore in equicorrente.
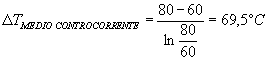

Figura 7. Diagramma T(x) in un caso particolare di scambiatore in controcorrente.
Dall’esempio riportato si nota come il DT m e d i o in controcorrente sia maggiore che in equicorrente e ciò comporta una maggiore potenza complessiva scambiata nel primo rispetto al secondo. Questo naturalmente avviene in quanto si è considerata la sezione S costante nei due casi. Per sopperire al minore apporto di potenza nel caso dell’equicorrente si agisce proprio sulla sezione e sulla superficie di contatto dei due liquidi. In compenso però abbiamo visto come l’equicorrente lavori più velocemente grazie alla maggiore differenza di temperatura iniziale DT(0). Quanto detto per l’aria calda è valido per qualsiasi liquido.
Finora abbiamo considerato unicamente lo scambiatore tubo in tubo che rappresenta il tipo più semplice in quanto la separazione fra i due liquidi è netta ed inoltre questi si muovono unicamente lungo l’asse delle x .Esistono però anche altri tipi di scambiatori in cui il liquido di servizio e quello servito si incrociano muovendosi in uno spazio tridimensionale.
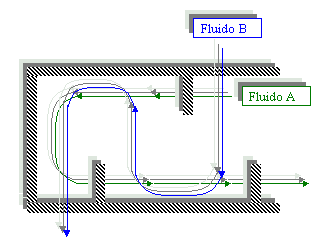
Figura 8. Scambiatore a doppio passo nel mantello.
In questo tipo di scambiatore si unisce la maggiore velocità di riscaldamento dell’uno e la maggiore potenza dell’altro. I calcoli su questo tipo di scambiatore sono più complicati in quanto i due liquidi non scorrono unicamente lungo l’asse delle x ma vengono a essere fra di loro ortogonali. Vi sono altri tipi di scambiatori che lavorano a contatto o meno quali SCAMBIATORI A PASSO MISTO o A PIASTRE CORRUGATE ma di questi non verrà fatta alcuna trattazione.
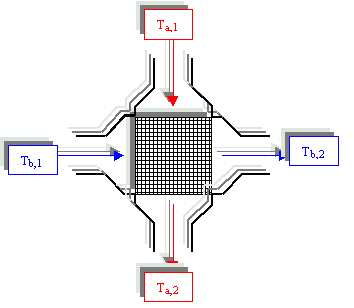
Figura 9. Scambiatore a correnti incrociate
N . B : Per scambiatori più complessi di quelli tubo in tubo come gli ultimi due esempi presentati entrano in gioco nella convezione forzata elementi non più costanti e quindi devo introdurre un coefficiente correttivo il quale mi tenga conto di questi fattori distorcenti. Questo coefficiente utilizzato per dimensionare il DT m e d i o a seconda del tipo di scambiatore viene indicato con F ed si trova diagrammato su tabulati del tipo raffigurato in figura 10 . Per ottenere l’effettiva differenza media di temperatura nei vari tipi di processi si utilizza la seguente formula :
![]() (18)
(18)
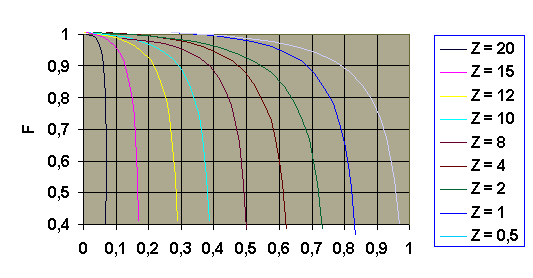
Figura 10. Grafico del fattore di penalizzazione F.
Sull’ascissa di questi grafici è riportato il valore adimensionale P il quale rappresenta l’efficacia del riscaldamento o del raffreddamento e può variare fra zero, nel caso che uno dei due fluidi sia a temperatura costante, a uno. Mentre il parametro Z , anch’esso adimensionale, che caratterizza le diverse curve è il rapporto fra le capacità termiche dei fluidi moltiplicate per la portata del fluido.
![]() (19)
(19)
![]() (20)
(20)
Dal grafico riportato si nota subito che :
ESERCIZI SUGLI SCAMBIATORI.
Esercizio 1. In un camino di altezza pari a 5m i fumi entrano a 260 °C ed escono a 253 °C. La temperatura dell’aria esterna con cui il camino scambia calore è di 0 °C. Calcolare il ? T m e d i o LOGARITMICO .
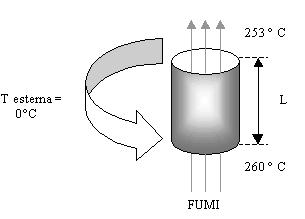
Figura 11. Camino di Esercizio1
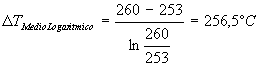
Si supponga ora che la portata dei fumi sia 1/10 di quella considerata. Se la quantità di calore scambiata è la stessa avrò che il raffreddamento dei fumi sarà maggiore e è quindi il salto di temperatura DT 2 fra aria e fumi all’uscita più grande. Supponiamo ad esempio che la temperatura dei fumi all’uscita sia di 190 °C.
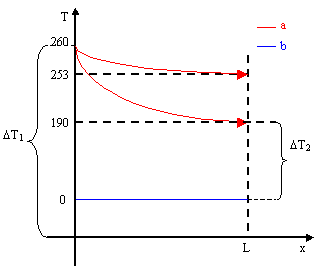
Allora il D T m e d i o LOGARITMICO diventa:
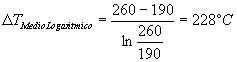
Mentre il valore medio lineare diventa :
![]()
Fra i due valori vi è uno scarto minimo e questo è giustificato dal fatto che uno dei due liquidi ,in questo caso l’aria esterna, che scambia calore è a temperatura costante e quindi approssima molto il DT m e d i o LOGARITMICO al valore lineare.
Esercizio 2. In uno scambiatore tubo in tubo scorrono rispettivamente, nel tubo interno azoto mentre nella camicia esterna acqua con una portata MH2O = 5000 Kg / h. La temperatura dell’acqua in ingresso è 20 °C. Trovare :
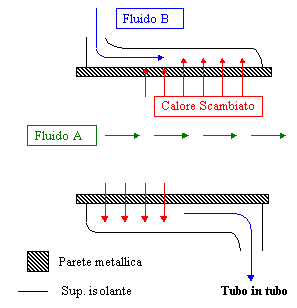
Figura 12. Scambiatore tubo in tubo
Indico con Di il diametro interno del tubo interno pari a 101mm e con De il diametro esterno del tubo interno pari a 108mm.Inoltre indico con D2 il diametro del tubo esterno pari a 125mm e di cui ignoro il materiale costituente in quanto non ho scambi con l’esterno.
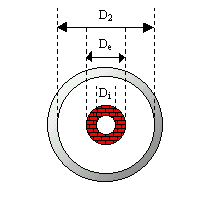
Figura 13. Sezione normale di uno scambiatore tubo in tubo
Riassumendo i dati in mostro possesso :

SOLUZIONE : ricaviamo la temperatura di uscita dell’acqua dal bilancio dell’energia. Ricaviamo il calore scambiato dall’azoto ricordando che siamo a pressione costante.
![]()
Questo è lo stesso calore scambiato dall’acqua in quanto questa è termicamente isolata dall’esterno. Otteniamo :
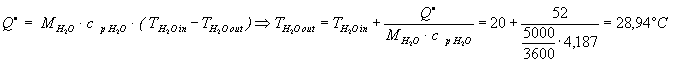
Devo applicare la terza relazione dell’energia Q = K · S · D T m e d i o LOGARITMICO prima in equicorrente poi in controcorrente :
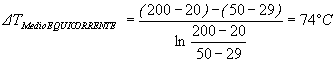
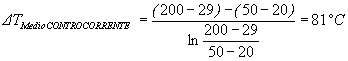
Ora dobbiamo cercare il coefficiente di scambio K per ottenere il calore scambiato nello scambiatore. Per far questo ricorriamo alle resistenze termiche :
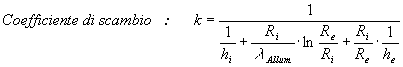 (20)
(20)
![]()
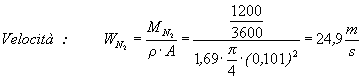
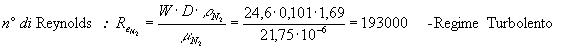
Dal numero di Reynolds si deduce che il regime dell’azoto, che si trova nel tubo interno in uno stato di convezione forzata, è turbolento. Infatti sappiamo che il valore critico di Reynolds che mi indica il passaggio dal regime laminare a quello turbolento è Re @ 2300. Quindi per ricavare il nostro coefficiente di convezione interna h i dobbiamo ricorrere al numero di Nusselt secondo l'equazione di Dittus-Boelter che ha validità per i fluidi correnti in tubo in regime turbolento.
![]()
![]()
Ora devo calcolare il coefficiente di convezione per l’acqua che sappiamo scorrere nella camicia esterna tenendo conto nei calcoli di Reynold, della velocità, ecc.. che essa assume una forma di corona circolare e quindi dovremo calcolare il diametro equivalente.
![]()
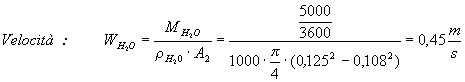
Si noti come la velocità dell’acqua sia molto inferiore a quella dell’azoto e ciò dovuto soprattutto a una maggiore densità del primo rispetto al secondo. Ora per trovare Reynolds devo calcolarmi il diametro idraulico equivalente Deq della corona circolare in quanto questa ha una geometria complessa:
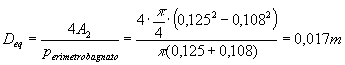
ove p è il perimetro bagnato dall'acqua. Ora posso calcolare Reynolds :
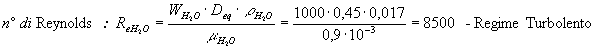
Il numero di Reynolds mi indica che non posso applicare, per trovare Nusselt, Dittus-Boelter, come riportato nella tabella qui sotto, in quanto ha validità da un numero di Reynolds pari a 10000 in su. Uso allora la formula di Böhm che vale fra 2500 e 10000.Applicando dunque la formula di Böhm ottengo il valore di Nusselt adeguato per ricavare il coefficiente di convezione h e lato acqua :
![]()
![]()
Allora ricavo il mio coefficiente di scambio visto nella formula (20) inserendo i valori trovati.
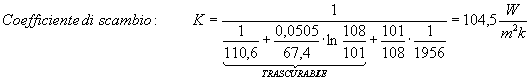
Considero unicamente la resistenza di convezione interna in quanto le resistenze termiche dell’acciaio sono trascurabili. Posso allora finalmente ricavare la lunghezza L del tubo nei casi di equicorrente e controcorrente che è quanto richiesto dal problema.
![]()
![]()