Onde sferiche:
Per trattare le onde sferiche è necessario ricavare l’equazione di D’Alambert in coordinate sferiche.
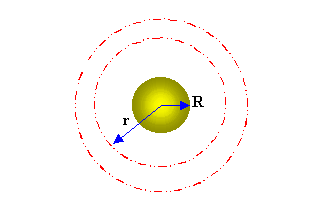
La sorgente del campo sonoro è una sfera in campo libero di raggio R, essa pulsa, quindi il suo raggio non rimane costante, ma varia in funzione del tempo t secondo la relazione R (t) = R0 + DR sin (wt), dove R0 indica il raggio della sfera a riposo.
Il campo sonoro è definito per valori di r > R.

Fig. 1 – Sfera sorgente del campo sonoro.
Per ottenere l’equazione di D’Alambert in coordinate sferiche utilizziamo un trucco affermando che il potenziale della velocità F(r, t) è funzione del tempo e della distanza dalla sfera, ma il prodotto FR rimane costante.
L’equazione da trattare risulta quindi essere la seguente:
![]() (1)
(1)
Svolgendo la derivata otteniamo:
![]() (2)
(2)
L’equazione così ottenuta è molto difficile da risolvere quindi operiamo, nella (1), la sostituzione Y = Fr ed otteniamo:
![]() (3)
(3)
La soluzione di questa equazione differenziale è data da :
![]() (4)
(4)
Il secondo termine di questa espressione rappresenta la parte di onde entranti nella sfera quindi, dato che ci occupiamo soltanto del campo sonoro all’estreno, esso non ha importanza e può essere trascurato.
Pertanto, operando la sostituzione inversa F = Y / r, otteniamo:
![]() (5)
(5)
Per far in modo che l’equazione (5) abbia significato fisico è necessario trascurare il termine immaginario dato dall’esponenziale complesso, quindi la forma definitiva del potenziale della velocità acustica è data da:
![]() (6)
(6)
Rimane ora da calcolare il valore di Y+, è necessario quindi imporre delle condizioni al contorno valide sulla pelle della sfera.
Sappiamo che:
![]() (7)
(7)
Imponiamo l’uguaglianza:
![]() (8)
(8)
Utilizzando le forme complete delle espressioni, vale a dire considerando anche la parte immaginaria, si ottiene che:
![]() (9)
(9)
Dalla (9) è immediato ricavare :
![]() (10)
(10)
Possiamo ora scrivere un’ espressione per la velocità acustica valida per un generico r > R :
![]() (11)
(11)
Calcoliamo ora l’espressione della pressione acustica e confrontiamola con quella della velocità.
Dall’espressione di F ricavata, otteniamo quella della pressione P mediante una semplice derivazione e riportiamo gli andamenti in un grafico.
![]() (12)
(12)
![]() (13)
(13)
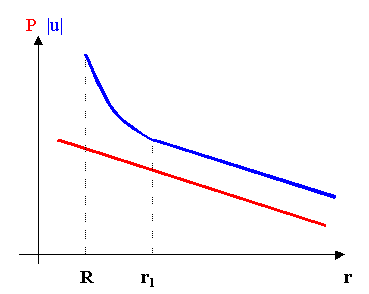
Fig. 2 – Pressione velocità sonora
Dal grafico si vede come pressione e velocità varino in fase per valori di r > rl, mentre per valori inferiori la velocità non varia più linearmente, questo è dovuto al fatto che u (r, t) dipende dal valore del prodotto kr = wr/c:
- kr < 1 : il termine che prevale nell’espressione di u è il primo (quello che si ottiene svolgendo la parentesi moltiplicando per 1) quindi ci troviamo in campo vicino alla sorgente e l’andamento non è lineare.
- kr >1 : il termine che prevale nell’espressione di u è il secondo (quello che si ottiene svolgendo la parentesi moltiplicando per jkr) quindi siamo in campo lontano dalla sorgente e l’andamento è lineare.
Per basse frequenze di pulsazione la zona in cui si estende il campo vicino è maggiore, per il fatto che k dipende da w secondo la relazione precedente, così che è necessario avere un valore di r maggiore per ottenere un prodotto kr > 1 e portarci in campo lontano, quindi per basse frequenze si ha un fenomeno d’amplificazione di queste ultime che viene detto effetto di campo vicino.
L’andamento della pressione non ha una doppia pendenza come la velocità quindi in campo vicino pressione e velocità non variano in fase, infatti, se calcoliamo l’impedenza
![]() (14)
(14)
vediamo come al variare di r varia il modulo ma anche la fase di Z, più ci avviciniamo alla sorgente, maggiormente i segnali sono sfasati.
Facciamo ora alcune considerazioni sui valori assunti dall’impedenza in due situazioni limite:
- Campo lontano:
![]() (15)
(15)
L’impedenza è la stessa che si ha per un’onda piana progressiva.
- Campo vicino:
![]() (16)
(16)
L’impedenza è puramente immaginaria, quindi pressione e velocità sono sfasate di 90° cosa che ci porterebbe ad affermare che il trasporto d’energia è nullo.
Questa situazione deriva dall’aver trascurato il termine jkr a denominatore, che in realtà non è del tutto trascurabile dato che ora ci troviamo di fronte ad un paradosso.
Calcoliamo l’intensità sonora:
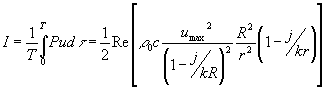 (17)
(17)
In campo lontano:
![]() (18)
(18)
L’intensità varia con il quadrato della distanza, in accordo con il fatto che essa è data dalla potenza diviso la superficie della sfera di raggio r nella cui espressione compare il quadrato del raggio, come si vede dalla seconda uguaglianza.
Possiamo quindi scrivere un’espressione per la pressione valida in campo lontano dalla sorgente:
![]() (19)
(19)
In campo vicino:
 (20)
(20)
Dove
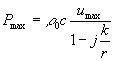
![]() (21)
(21)
Il termine tra parentesi tonde diminuisce al diminuire della distanza r, quindi anche la potenza diminuisce.
La potenza totale rimane sempre la stessa, ma è divisa in due contributi:
- Potenza attiva, contributo visibile
- Potenza reattiva, contributo non visibile.
Vicino alla sorgente nella potenza totale è prevalente il contributo dalla potenza reattiva mentre, lontano dalla sorgente è prevalente il contributo della potenza attiva.
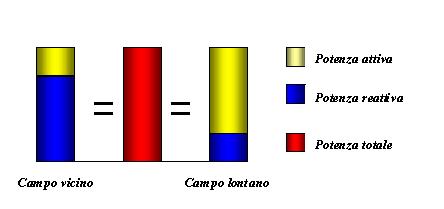
Fig. 3 – Diagramma di ripartizione delle potenze
Somma di suoni e definizione del Bel
Sonorità:
La sonorità non è un’unità di misura ma una scala e si indica con la lettera S, l’aumento di una sonorità di un suono significa che esso è udito di sonorità doppia rispetto al precedente, quindi ad esempio, un suono con S = 3 ha sonorità doppia rispetto ad un suono con S = 2 il quale a sua volta ha sonorità doppia rispetto ad un suono con S = 1.
Livello sonoro:
![]() misurato in BEL (22)
misurato in BEL (22)
Dove I0 è un valore di riferimento che indica l’intensità del suono più debole udibile dall'uomo.
Il livello L è quindi maggiore di zero per ogni suono udibile.
L’unità di misura correntemente utilizzata per il livello sonoro è un sottomultiplo del BEL, il decibel (dB), per questo motivo si introduce un fattore 10 nell’espressione:
![]() misurato in dB (23)
misurato in dB (23)
Nell’ipotesi d’onda piana progressiva sono valide le seguenti relazioni:
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
quindi il livello sonoro può essere calcolato mediante una delle seguenti formule:
![]() (29)
(29)
Sperimentalmente si è ricavato che:
P0 = 20 mPa u0 = 5 10-8 m/s I0 = 10-12 W/m2
Nel calcolo dei livelli sonori valgono le seguenti regole:
- Un raddoppio d’intensità sonora comporta un aumento del livello sonoro di 3db.
- Un raddoppio della potenza sonora comporta un aumento del livello sonoro di 6 dB.
Vediamo ora un esempio di somma di due suoni:
Abbiamo due sorgenti sonore A e B ed un microfono posto tra le due, vogliamo calcolare il livello sonoro nel punto in cui si trova il microfono.
Prendiamo:
LA = LB = 40 dB
Se i due suoni sono diversi ma hanno la stessa intensità IA = IB sonora, il livello sonoro totale si ottiene nel seguente modo:
![]()
Se i due suoni sono uguali ed il microfono si trova alla stessa distanza da entrambe le sorgenti, il livello sonoro totale si ottiene utilizzando le pressioni PA = PB, nel seguente modo :
![]()
![]()