ANALISI STATISTICA
L’analisi statistica si applica quando si ha che fare con un rumore variabile nel tempo; il solo valore del livello equivalente non e’ sufficiente quando si vuole venire a conoscenza di cosa e’ successo durante il periodo di analisi. In pratica non e’ in grado di dirmi se il rumore e’ variato o e’ stato circa costante durante il periodo. L’analisi statistica viene fatta utilizzando un istogramma che rappresenta in ascissa il livello sonoro ed in ordinata la percentuale del tempo di misura in cui e’ stato presente quel determinato livello sonoro. L’istogramma e’ un grafico ad immediata percezione visiva; non e’ una curva continua, ma e’ formato da una serie di rettangoli che hanno una base sull’ascissa ad un determinato livello sonoro e l’altra base si innalza e si posiziona in corrispondenza della precisa percentuale di tempo di misura a cui corrisponde il livello. Normalmente l’ampiezza delle basi su di un istogramma sono fatte per classi larghe ˝dB. E’ poi evidente che la somma delle percentuali a cui sono arrivate le basi superiori dei rettangoli corrispondenti ai vari livelli deve fare 100%.
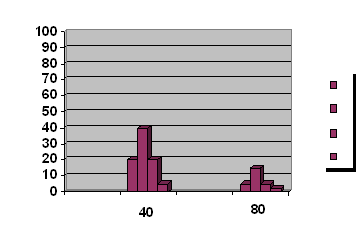 Considerando il fonometro bisogna osservare che durante la misura esso campiona i dati della misura statistica, ma non e’ in grado di visualizzarli sul proprio display. E’ necessario quindi per disporre di tali dati l’utilizzo di un computer collegato serialmente col fonometro. Facciamo ora l’esempio di una stanza in sia azionato ad intermittenza un ventilatore abbastanza rumoroso con livello sonoro intorno agli 80dB contro un rumore di fondo di 40dB. L’analisi statistica distributiva di questo fenomeno e’ rappresentata da un grafico molto significativo.
Considerando il fonometro bisogna osservare che durante la misura esso campiona i dati della misura statistica, ma non e’ in grado di visualizzarli sul proprio display. E’ necessario quindi per disporre di tali dati l’utilizzo di un computer collegato serialmente col fonometro. Facciamo ora l’esempio di una stanza in sia azionato ad intermittenza un ventilatore abbastanza rumoroso con livello sonoro intorno agli 80dB contro un rumore di fondo di 40dB. L’analisi statistica distributiva di questo fenomeno e’ rappresentata da un grafico molto significativo.
Ricordo che in ascissa e’ presente il livello sonoro, mentre in ordinata la %. Ottengo cosi’ 2 zone del grafico ben limitate; alla zona intorno ai 40dB corrisponde il rumore di fondo, mentre alla zona intorno agli 80dB corrisponde il rumore del ventilatore. Da questo grafico posso infine ricavare i vari livelli equivalenti:
Li/10
Leq= 10log[S
(fraz.%)*(10 )]
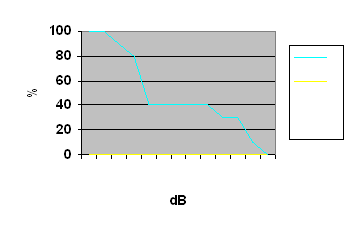 Avendo la possibilita’ di trovare Leq per ogni banda di livello. In questo modo posso ricavare il livello equivalente come se il ventilatore non ci fosse ed allo stesso modo ricavare il livello equivalente del ventilatore come se il rumore di fondo non ci fosse. In pratica, dato che tra il rumore di fondo e quello del ventilatore ci sono 40dB di differenza, per trovare il livello equivalente totale sommare il contributo del rumore di fondo non e’ poi cosi’ importante. Oltre all’analisi distributiva e’ possibile poi fare un’analisi cumulativa. Nel grafico per la rappresentazione di questo tipo di analisi rimangono nelle ordinate la percentuale del tempo di misura a cui e’ stato presente un livello sonoro e nelle ascisse il livello sonoro stesso. Definiamo ora il concetto di Lmin che rappresenta l’angolo di sinistra del primo rettangolo relativo ai 40dB e Lmax che rappresenta l’angolo di destra dell’ultimo rettangolo relativo agli 80dB. La curva cumulativa e’ una curva a "scalini": parte dal 100% dell’asse delle ordinate, si sposta a destra fino a quando non incrocia la retta verticale posizionata su Lmin e quindi comincia a decrescere di una percentuale pari alla percentuale alla quale era arrivato il rettangolo a cui corrispondeva quel livello. Passato il livello intorno ai 40dB la curva continua a spostarsi costantemente verso destra ed infine raggiunge la zona degli 80dB. Continua a decrescere a scalino fino a terminare in Lmax, dove si interseca con l’asse delle ascisse e si ferma.
Avendo la possibilita’ di trovare Leq per ogni banda di livello. In questo modo posso ricavare il livello equivalente come se il ventilatore non ci fosse ed allo stesso modo ricavare il livello equivalente del ventilatore come se il rumore di fondo non ci fosse. In pratica, dato che tra il rumore di fondo e quello del ventilatore ci sono 40dB di differenza, per trovare il livello equivalente totale sommare il contributo del rumore di fondo non e’ poi cosi’ importante. Oltre all’analisi distributiva e’ possibile poi fare un’analisi cumulativa. Nel grafico per la rappresentazione di questo tipo di analisi rimangono nelle ordinate la percentuale del tempo di misura a cui e’ stato presente un livello sonoro e nelle ascisse il livello sonoro stesso. Definiamo ora il concetto di Lmin che rappresenta l’angolo di sinistra del primo rettangolo relativo ai 40dB e Lmax che rappresenta l’angolo di destra dell’ultimo rettangolo relativo agli 80dB. La curva cumulativa e’ una curva a "scalini": parte dal 100% dell’asse delle ordinate, si sposta a destra fino a quando non incrocia la retta verticale posizionata su Lmin e quindi comincia a decrescere di una percentuale pari alla percentuale alla quale era arrivato il rettangolo a cui corrispondeva quel livello. Passato il livello intorno ai 40dB la curva continua a spostarsi costantemente verso destra ed infine raggiunge la zona degli 80dB. Continua a decrescere a scalino fino a terminare in Lmax, dove si interseca con l’asse delle ascisse e si ferma.
In pratica questa curva rappresenta la % di tempo in cui si e’ superato un certo livello sonoro. L’informazione e’ in pratica la stessa che ci fornisce l’analisi distributiva, allora a cosa serve? Serve per introdurre il concetto di livello "percentile". Un livello percentile e’ ottenuto partendo dall’asse delle ordinate ad una certa percentuale spostandosi a destra fino a quando si incontra la curava cumulativa; qiondi si scende in verticale fino ad incrociare l’asse delle ascisse e in questo punto leggo il livello relativo a quella percentuale. Ad esempio il L90 o livello percentile 90 e’ quel livello che per il 90% del tempo e’ stato superato. Bisogna prestare molta attenzione al fatto che L50 non e’ la stessa cosa che Leq perche’ il secondo livello non e’ una media aritmetica, ma energetica (i dB hanno una scala logaritmica).
Un fatto molto importante da non trascurare e’ che l’analisi statistica ha senso solo se si considerano i valori esponenziali RMS con costante di tempo Fast, cioe’ la costante di tempo RC e’ uguale a 0,125 secondi. Questo perche’ questo valore corrisponde approssimativamente al tempo di risposta dell’udito umano. Vediamo ora quale e’ pero’ il significato pratico di un livello percentile: quando uno strumento misura il livello sonoro, memorizza automaticamente dai 3 ai 5 percentili (o quelli relativi a 10/50/90% o 5/10/50/90/95%) inoltre memorizza anche Lmin e Lmax. In genere mi trovo quindi sul display 5 punti dai quali non posso di certo ricostruire la curva distributiva, ma posso comunque ottenere informazioni molto interessanti: se L10=60 e L90=61dB questo significa che il clima acustico e poco variabile; mentre se L10=30 e L90=90dB questo significa che il clima acustico e’ estremamente variabile.
Se un rumore e’ stabile esso non da’ fastidio all’udito umano; cio’ che disturba e’ il rumore fortemente variabile. Da notare che se il rumore del ventilatore fosse stato costante avrei avuto un livello equivalente maggiore, ma un fastidio all’udito minore a causa di quello che e’ chiamato meccanismo fisiologico. L’enorme vantaggio dell’analisi statistica, oltre al fatto di essere di immediata lettura, e’ il fatto che il numero di numeri che devo considerare non cresce al crescere del tempo. Rappresenta quindi una tecnica di riduzione dei dati, pur consentendomi di conservare le informazioni necessarie a separare le sorgenti dei rumori. Questo e’ un aspetto molto importante perche’ spesso avere per le mani troppi numeri complica a dismisura l’analisi e aumenta le possibilita’ di commettere errori.
INTENSIMETRIA
In genere l’intensita’ acustica e’ calcolabile conoscendo la pressione acustica "p" e la velocita’ delle particelle "u". Il problema che si verifica usualmente e’ il fatto che i microfoni normalmente in commercio misurano solo p, non u; misurare l’intensita’ diventa pero’ possibile utilizzando 2 microfoni posti ad una distanza d. Quando un’onda sonora passa longitudinalmente ai 2 microfoni vengono fatte due letture: p(1) e p(2). Mediante l’utilizzo dell’equazione di Eulero posso allora calcolare u: u=-ò
grad(p/r
)dt. Se l
>>d approssimando posso sostituire una retta passante per p(1) e p(2) al tratto di sinusoide dell’onda che effettivamente passerebbe ed otterrei: gradp=(p(2)-p(1)0/d.
Per compiere un rilevamento di intenista’ e’ in generale consigliabile utilizzare i due microfoni in fase per evitare di ricorrere al calibratore per calibrarli o di incorrere in noiosi effetti disturbativi dovuti al disaccoppiamento di fase dei due microfoni. Definiamo ora l’indice di reattivita’ del campo: Lk=Ld-LI. Tanto piu’ indice di reattivita’e’ alto tanto piu’ e’ difficile misurare soprattutto alle basse frequenze. E’ fondamentale notare che se I va dal microfono 1 a quello 2 I>0, mentre se I va dal microfono 2 a quello 1 I<0. L’intensimetro misura la componente cartesiana dell’intensita’ lungo l’asse che congiunge i due microfoni. Appare evidente da questo fatto che se arriva perpendicolarmente alla retta congiungente I=0. Consideriamo ora 2 altoparlanti posti uno di fronte all’altro: notiamo che se il suono arriva da destra la somma p+u=2p sull’altoparlante di destra, mentre p-u=0 sull’altoparlante di sinistra. Se il suono arriva da sinistra la somma p+u=0 sull’altoparlante di destra e p-u=2p sull’altoparlante di sinistra. Se infine il suono arriva perpendicolarmente sull’altoparlante di destra p+u=p e su quello di sinistra p-u=p. La tecnica ottimale e’ quella utilizzata per gli impianti stereofonici, la tecnica Blumlein: questa tecnica pone gli altoparlanti sui vertici della base di un triangolo equilatero, rivolti verso l’ascoltatore posizionato sul vertice opposto.
Misurare l’intensita’ e’ una tecnica ideale anche per misurare il livello di potenza: P=å
IniAi=ImiAtot=ò
I*n*dA dove a e’ la superficie di inviluppo che viene coperta mediante la tecnica dello spazzolamento. La cosa importante di questa tecnica e’ che la vicinanza di un’altra sorgente di rumore non disturba la misura, perche’ la quantita’ di rumore esterno che entra e’ pari a quella che esce grazie al fatto che la normale n e’ presa sempre uscente dalla superficie.
 Considerando il fonometro bisogna osservare che durante la misura esso campiona i dati della misura statistica, ma non e’ in grado di visualizzarli sul proprio display. E’ necessario quindi per disporre di tali dati l’utilizzo di un computer collegato serialmente col fonometro. Facciamo ora l’esempio di una stanza in sia azionato ad intermittenza un ventilatore abbastanza rumoroso con livello sonoro intorno agli 80dB contro un rumore di fondo di 40dB. L’analisi statistica distributiva di questo fenomeno e’ rappresentata da un grafico molto significativo.
Considerando il fonometro bisogna osservare che durante la misura esso campiona i dati della misura statistica, ma non e’ in grado di visualizzarli sul proprio display. E’ necessario quindi per disporre di tali dati l’utilizzo di un computer collegato serialmente col fonometro. Facciamo ora l’esempio di una stanza in sia azionato ad intermittenza un ventilatore abbastanza rumoroso con livello sonoro intorno agli 80dB contro un rumore di fondo di 40dB. L’analisi statistica distributiva di questo fenomeno e’ rappresentata da un grafico molto significativo.  Avendo la possibilita’ di trovare Leq per ogni banda di livello. In questo modo posso ricavare il livello equivalente come se il ventilatore non ci fosse ed allo stesso modo ricavare il livello equivalente del ventilatore come se il rumore di fondo non ci fosse. In pratica, dato che tra il rumore di fondo e quello del ventilatore ci sono 40dB di differenza, per trovare il livello equivalente totale sommare il contributo del rumore di fondo non e’ poi cosi’ importante. Oltre all’analisi distributiva e’ possibile poi fare un’analisi cumulativa. Nel grafico per la rappresentazione di questo tipo di analisi rimangono nelle ordinate la percentuale del tempo di misura a cui e’ stato presente un livello sonoro e nelle ascisse il livello sonoro stesso. Definiamo ora il concetto di Lmin che rappresenta l’angolo di sinistra del primo rettangolo relativo ai 40dB e Lmax che rappresenta l’angolo di destra dell’ultimo rettangolo relativo agli 80dB. La curva cumulativa e’ una curva a "scalini": parte dal 100% dell’asse delle ordinate, si sposta a destra fino a quando non incrocia la retta verticale posizionata su Lmin e quindi comincia a decrescere di una percentuale pari alla percentuale alla quale era arrivato il rettangolo a cui corrispondeva quel livello. Passato il livello intorno ai 40dB la curva continua a spostarsi costantemente verso destra ed infine raggiunge la zona degli 80dB. Continua a decrescere a scalino fino a terminare in Lmax, dove si interseca con l’asse delle ascisse e si ferma.
Avendo la possibilita’ di trovare Leq per ogni banda di livello. In questo modo posso ricavare il livello equivalente come se il ventilatore non ci fosse ed allo stesso modo ricavare il livello equivalente del ventilatore come se il rumore di fondo non ci fosse. In pratica, dato che tra il rumore di fondo e quello del ventilatore ci sono 40dB di differenza, per trovare il livello equivalente totale sommare il contributo del rumore di fondo non e’ poi cosi’ importante. Oltre all’analisi distributiva e’ possibile poi fare un’analisi cumulativa. Nel grafico per la rappresentazione di questo tipo di analisi rimangono nelle ordinate la percentuale del tempo di misura a cui e’ stato presente un livello sonoro e nelle ascisse il livello sonoro stesso. Definiamo ora il concetto di Lmin che rappresenta l’angolo di sinistra del primo rettangolo relativo ai 40dB e Lmax che rappresenta l’angolo di destra dell’ultimo rettangolo relativo agli 80dB. La curva cumulativa e’ una curva a "scalini": parte dal 100% dell’asse delle ordinate, si sposta a destra fino a quando non incrocia la retta verticale posizionata su Lmin e quindi comincia a decrescere di una percentuale pari alla percentuale alla quale era arrivato il rettangolo a cui corrispondeva quel livello. Passato il livello intorno ai 40dB la curva continua a spostarsi costantemente verso destra ed infine raggiunge la zona degli 80dB. Continua a decrescere a scalino fino a terminare in Lmax, dove si interseca con l’asse delle ascisse e si ferma.