RIASSUNTO DELLA LEZIONE DEL GIORNO 16/11/98
ore 8.30-10.30
di JACOPO ALEOTTI
n° di matricola : 106334
ARGOMENTI DELLA LEZIONE :
1) EQUAZIONI DEL MOTO ISOTERMO DEI FLUIDI
1.a) EQUAZIONE DI CONTINUITA'
1.b) EQUAZIONE DI NAVIER
2) CENNI ALLA TEORIA DEI MODELLI
1
EQUAZIONI DEL MOTO ISOTERMO DEI FLUIDI
Sia V la regione dello spazio che contiene il sistema fluidodinamico che si vuole studiare . Le equazioni del moto dei fluidi sono due equazioni differenziali che hanno come dominio i punti di V ; per la loro risoluzione occorre assegnare in ogni situazione le opportune condizioni al contorno , esse vanno applicate al confine (o "pelle") di V :

Possibili condizioni al contorno sono :
SET DI VARIABILI :
INCOGNITE :
Per risolvere un problema di fluidodinamica bisogna determinare:
Occorrono quindi 5 equazioni differenziali indipendenti :
1.a
EQUAZIONE DI CONTINUITA'
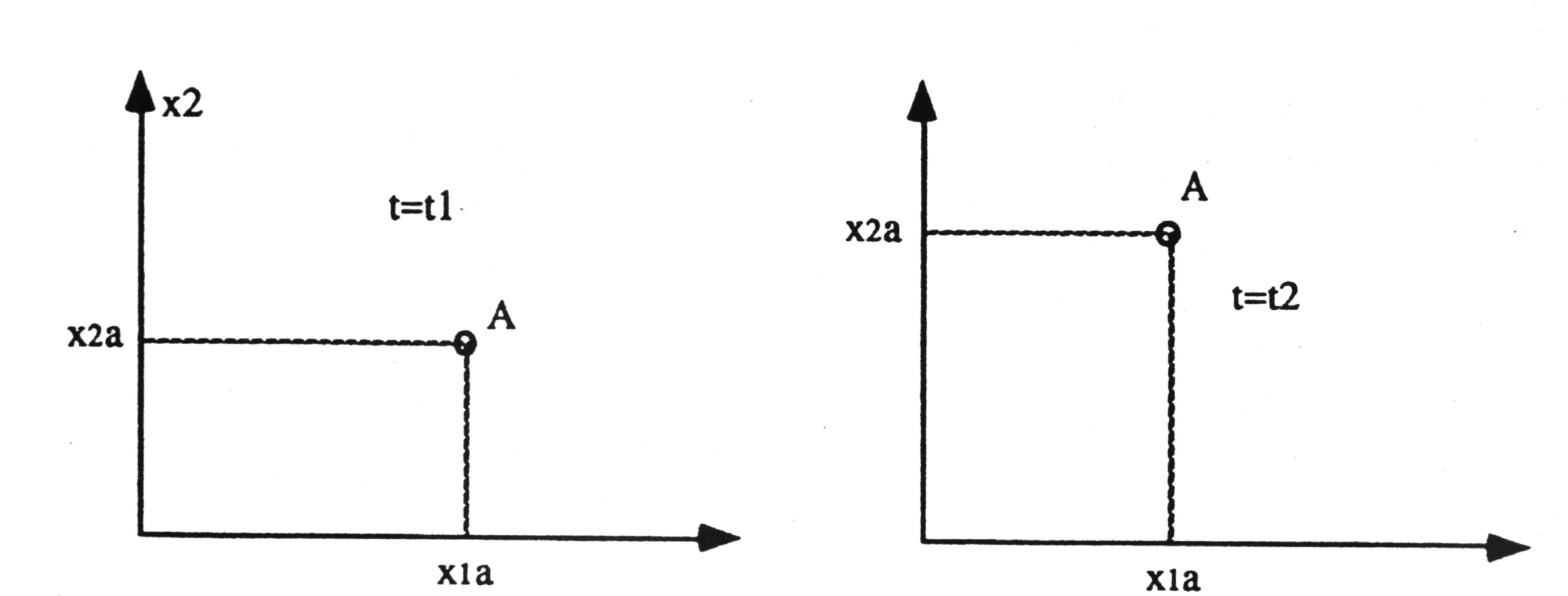
Si adotta un procedimento detto EULERIANO : Il volume V è visto come un sistema aperto in quiete (detto volume di controllo) . L'osservatore è fisso e segue il moto della particella nello spazio al variare del tempo : per esempio data una particella A in un sistema bidimensionale , le sue coordinate (x1a,x2a) all'istante t=t1 saranno diverse dalle sue coordinate all'istante t=t2 a causa del moto di A.
L'equazione di continuità esprime il concetto generale di conservazione della massa :
variazione netta della massa di V nell'unità di tempo = massa entrata in V nell'unità di tempo
Si consideri un volumetto infinitesimo dV=dxdydz appartenente al sistema :
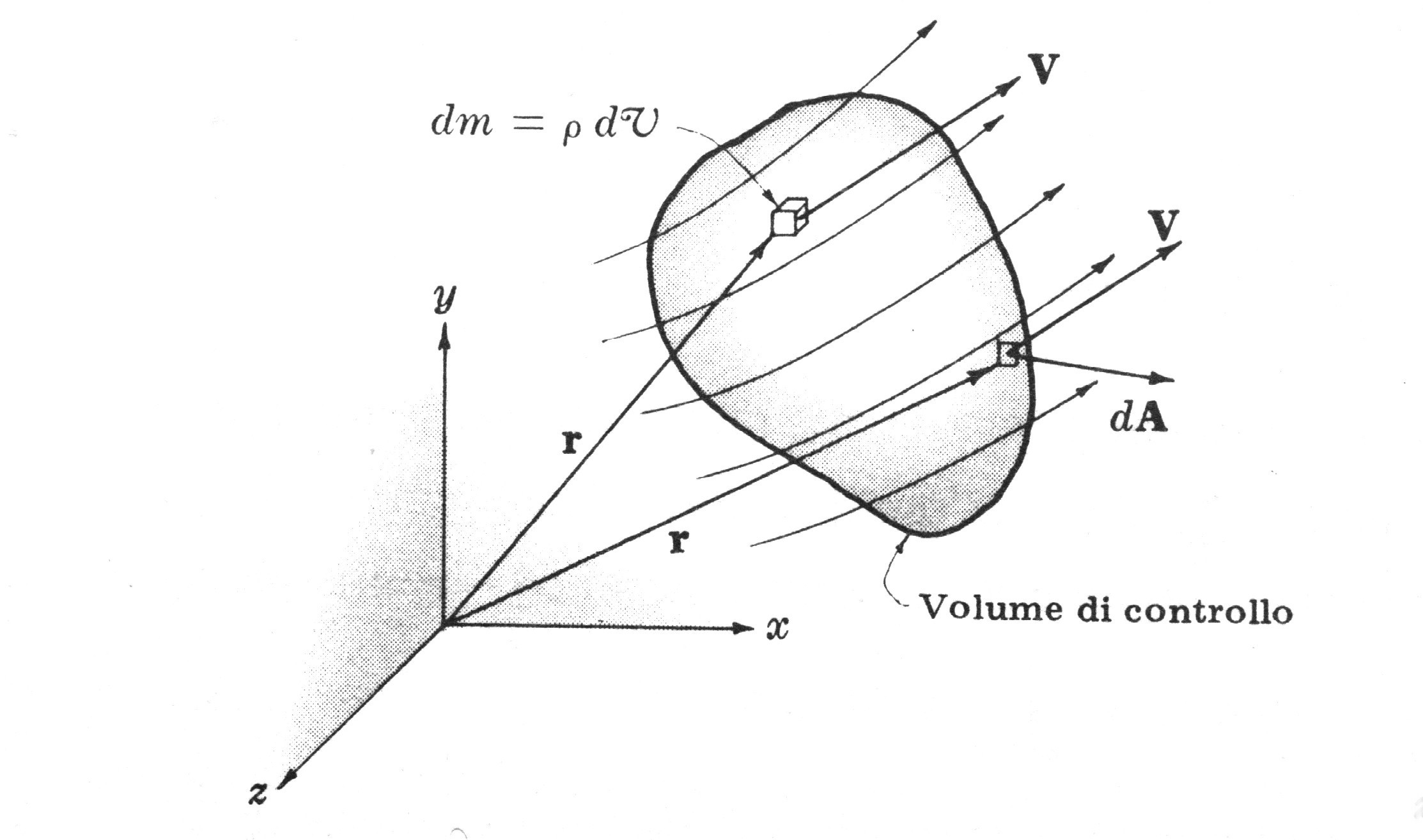
Nella figura dA=dS=ndS dove S è la superficie che racchiude V e n è il versore normale alla superficie alla coordinata r ; dS quindi è un vettore infinitesimo che è uscente da S ed ha come modulo dS . Sempre nella figura v (che in seguito verrà indicato con u) è il vettore velocità dell'elemento di fluido in prossimità della parete.
Si assumono positivi i versi delle normali uscenti da S :
Per quanto riguarda la densità del fluido essa è definita punto per punto :
![]()
Mentre all'interno del volumetto la densità è assunta costante e soddisfa la relazione :
![]()
Allora :
u·ndt = Spostamento dell'elemento di fluido prossimo a dS verso l'esterno nel tempo dt
u·ndSdt = Volume di fluido che esce da dS nel tempo dt
(dove l'operatore · indica il prodotto scalare di due vettori).
Moltiplicando l'ultima grandezza calcolata per la densità e dividendo per dt si ottiene la portata in massa che esce da dS cioè :
![]()
Infine integrando su S e cambiando di segno si ottiene la portata in massa che entra in V:
![]()
Essendo poi la variazione netta di massa in V data da :
![]()
Si ottiene l'equazione di continuità in forma integrale :
![]()
E' possibile riscrivere il secondo membro dell'equazione applicando il teorema di Gauss (che afferma che il flusso di un vettore attraverso una superficie chiusa S è uguale all'integrale esteso al volume racchiuso da S della divergenza del vettore) :
![]()
Inoltre poichè nel primo membro della equazione di continuità la derivata rispetto al tempo e il simbolo di integrale possono commutarsi si ha :
![]()
Quindi :
![]()
Poichè l'ultima equazione vale indipendentemente dal particolare V scelto si deduce che l'integrale su V è nullo se e solo se :
![]()
che rappresenta l'equazione di continuità in forma locale .
In regime stazionario tutte le derivate rispetto al tempo si annullano , se poi la densità è assunta costante in ogni punto di V :
![]()
Sotto queste ipotesi la divergenza del campo di velocità è nulla , il vettore velocità è detto SOLENOIDALE .
Diamo le definizioni di linea di corrente e di tubo di flusso :
LINEA DI CORRENTE: E' la linea tangente in ogni punto al vettore velocità dell'elemento di fluido in moto . In condizioni stazionarie le linee di corrente in un condotto sono invarianti nel tempo.
TUBO DI FLUSSO : E' l'insieme delle linee di corrente che passano per i punti di una linea piana chiusa e per tutti i punti interni ad essa .
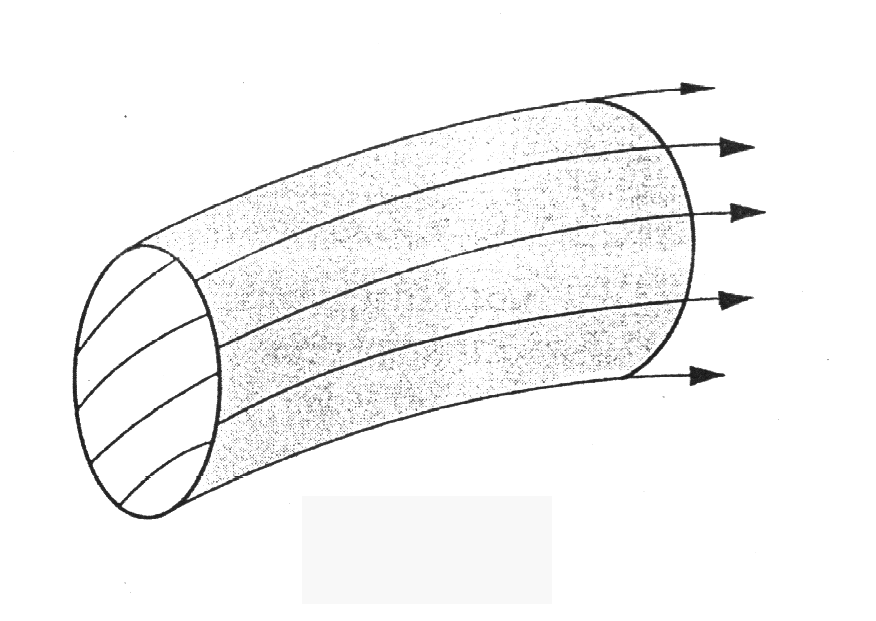
Il fluido quindi è confinato all'interno del tubo di flusso , può entrare ed uscire solo dalle superfici estreme e non dalla superficie laterale :
![]()
Quindi se u è solenoidale, applicando l'equazione di continuità ad un tubo di flusso si ha che la portata in massa uscente uguaglia ,in modulo, la portata in massa entrante :
![]()
Nell'ipotesi di considerare un problema monodimensionale di un fluido ideale che scorre in un condotto in cui la velocità è costante in ogni sezione , la portata in massa è data da:
![]()
La portatain massa dipende dalla densità dalla sezione del condotto e dalla velocità
ESEMPI :
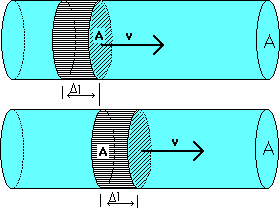
Se il condotto ha una sezione uniforme la velocità è costante.
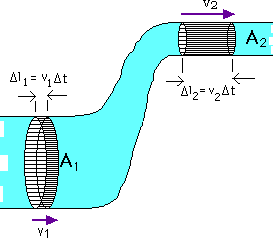
Se il condotto subisce delle strozzature la velocità cambia perchè la portata in massa si deve conservare.
1.b
EQUAZIONE DI NAVIER
.jpg)
Si adotta un procedimento detto LAGRANGIANO : il sistema in esame è un elemento di fluido che si muove lungo la sua traiettoria . L'osservatore si trova in un sistema di riferimento mobile solidale all'elemento di fluido stesso.
Sia F è una generica grandezza scalare che caratterizza la particella A , nel sistema di riferimento assoluto (fisso) si utilizza una rappresentazione matematica della grandezza F di questo tipo:
F=F(x,y,z,t)
Perchè si è interessati alla distribuzione di F come campo spaziale che si evolve nel tempo . In altre parole mentre nel procedimento Euleriano si fissava l'attenzione sulla particella , ora con il procedimento Lagrangiano si fissa l'attenzione sui punti dello spazio.
Il differenziale di F vale :
![]()
e quindi :
![]()
Questa grandezza è detta DERIVATA SOSTANZIALE di F dove
![]()
è il vettore velocità dell'elemento di fluido considerato . Nell'espressione della derivata sostanziale i primi tre termini sono detti del TRASPORTO mentre l'ultimo è la derivata parziale della grandezza F rispetto al tempo. I termini del trasporto rendono conto del moto dell'osservatore rispetto al sistema di riferimento assoluto.
Calcolo della accelerazione della particella :
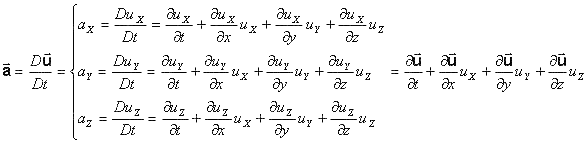
L'equazione di Navier è la formulazione della seconda legge della dinamica per un elemento di fluido :
![]()
tenendo conto che il vettore a è la derivata sostanziale del vettore u si può riscrivere l'equazione in questo modo :
![]()
Il vettore f rappresenta la risultante delle forze che agiscono sul volumetto infinitesimo di fluido considerato , i vari contributi sono dati da :
FORZE DI MASSA
FORZE DI VOLUME
FORZE DI MASSA :
Le forze di massa sono dovute all'azione del campo gravitazionale terrestre che , essendo conservativo , ammette un potenziale che vale (gz) per unità di massa , dove (g) è il modulo del vettore accelerazione di gravità . La forza per unità di massa si ottiene come gradiente di questo potenziale :
![]()
FORZE DI VOLUME:
Le forze di volume sono trasmesse alla particella dagli altri elementi di fluido ad essa adiacenti , possono essere forze di pressione o forze dovute alla viscosità del fluido :
Forze di pressione :
Analizziamo le componenti della risultante delle forze di pressione :
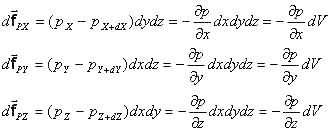
Sommando tutti i termini si ottiene che la risultante delle forze di pressione vale :
![]()
Forze viscose:
Consideriamo ancora l'elemento di volume , su di esso agiranno degli sforzi tangenziali (indicati con la lettera greca "tau") che sono responsabili delle forze viscose interne al fluido; in figura sono rappresentati tutti gli sforzi nella sola direzione y :
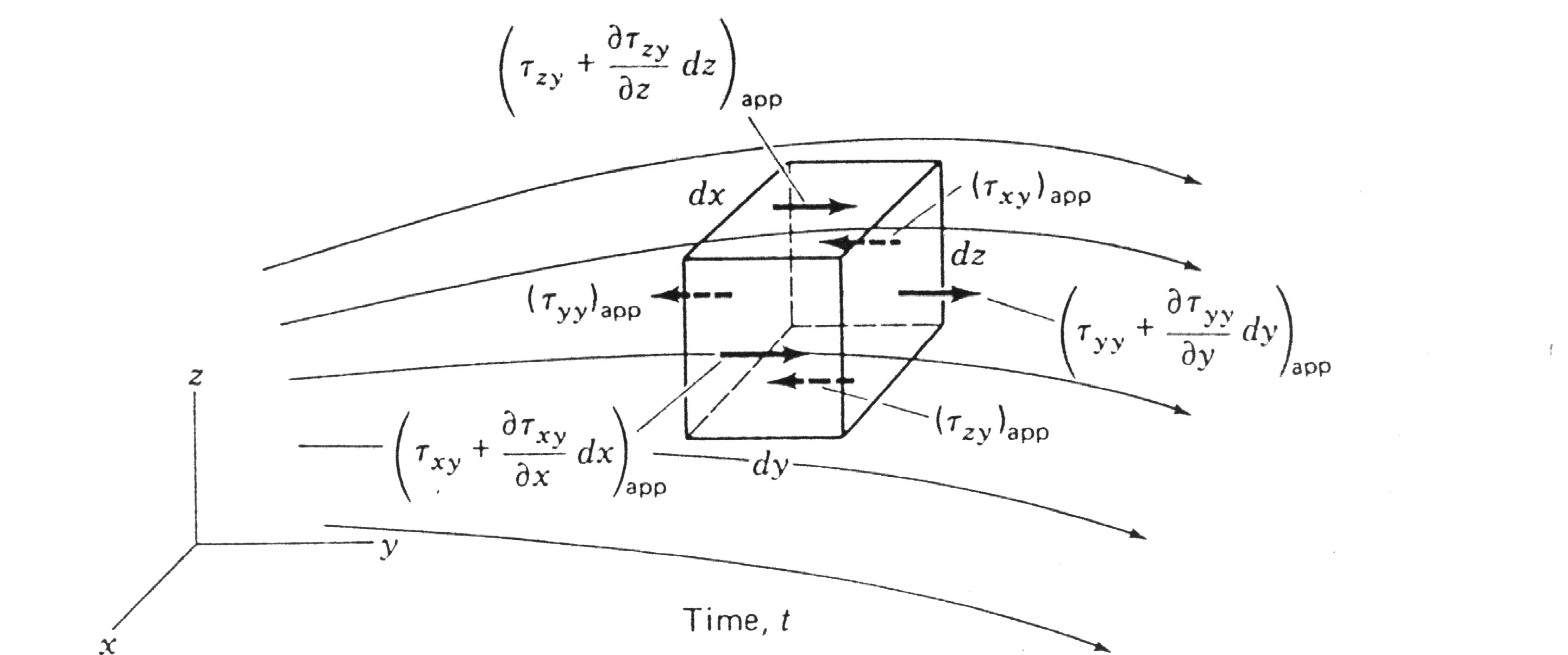
Scriviamo la risultante degli sforzi nella direzione y :
![]()
Ricordando la definizione di sforzo tangenziale si ha :
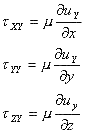
Si ottiene :
![]()
Tenendo conto infine anche delle componenti dello sforzo lungo x e lungo z (che si determinano in modo analogo) si ottiene lo sforzo complessivo :
![]()
Avendo introdotto nell'ultimo passaggio il Laplaciano di una funzione vettoriale.
L'equazione di Navier si potrà quindi scrivere nel seguente modo :
![]()
Sostituendo i termini calcolati precedentemente si ottiene :
![]()
Ed infine dividendo per la densità :
![]()
L'ultima espressione è l'equazione di NAVIER per un fluido INCOMPRESSIBILE nel quale non vi è variazione di massa nel volumetto di fluido considerato durante l'intervallo infinitesimo di tempo dt . Rimuovendo anche questa ipotesi l'equazione si può generalizzare se il fluido è Newtoniano . Infatti per un fluido newtoniano vale la seguente definizione generale di viscosità dinamica :
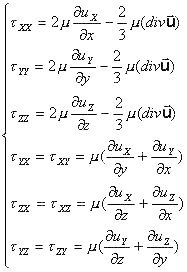
Questa definizione comporta una variazione del contributo dovuto alle forze viscose . Con le opportune sostituzione si ottiene l'equazione di Navier scritta in regime non stazionario :
![]()
In condizioni stazionarie (div(u)=0) ci si riconduce al caso del moto di un fluido incompressibile perchè l'ultimo termine , dato dal gradiente della divergenza di u , si annulla.
Infine , nel caso di un fluido perfetto (viscosità dinamica nulla) l'equazione di Navier si semplifica in questo modo :
![]()
detta equazione di EULERO .
Sono noti pochi casi semplici in cui è possibile trovare una soluzione analitica all'equazione di Navier:
Problema di POISEUILLE : moto laminare a regime di un fluido in un condotto di sezione circolare e di raggio R :
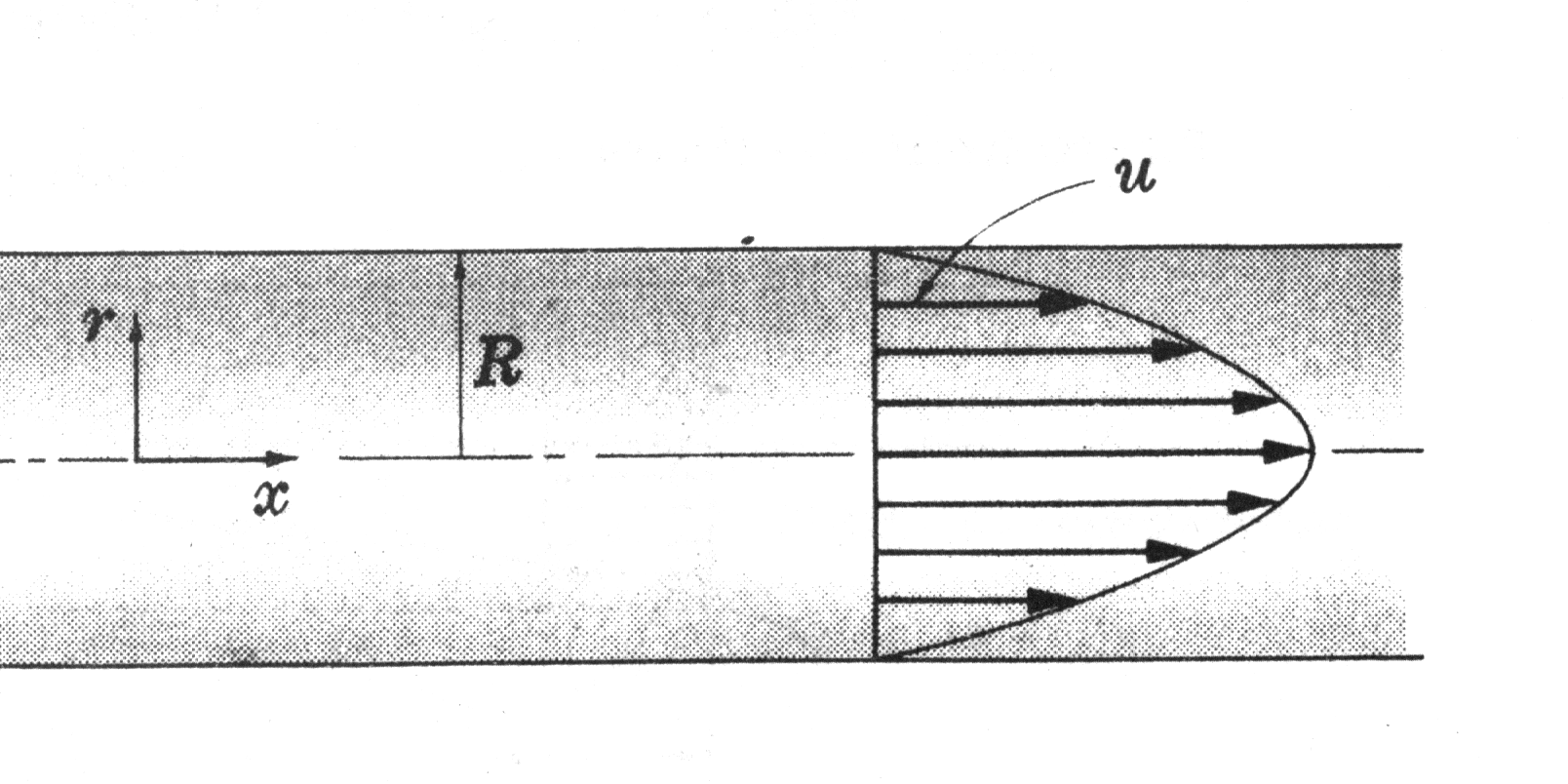
Moto laminare a regime di un fluido che scorre entro due superfici piane affacciate infinite separate da una distanza 2h:
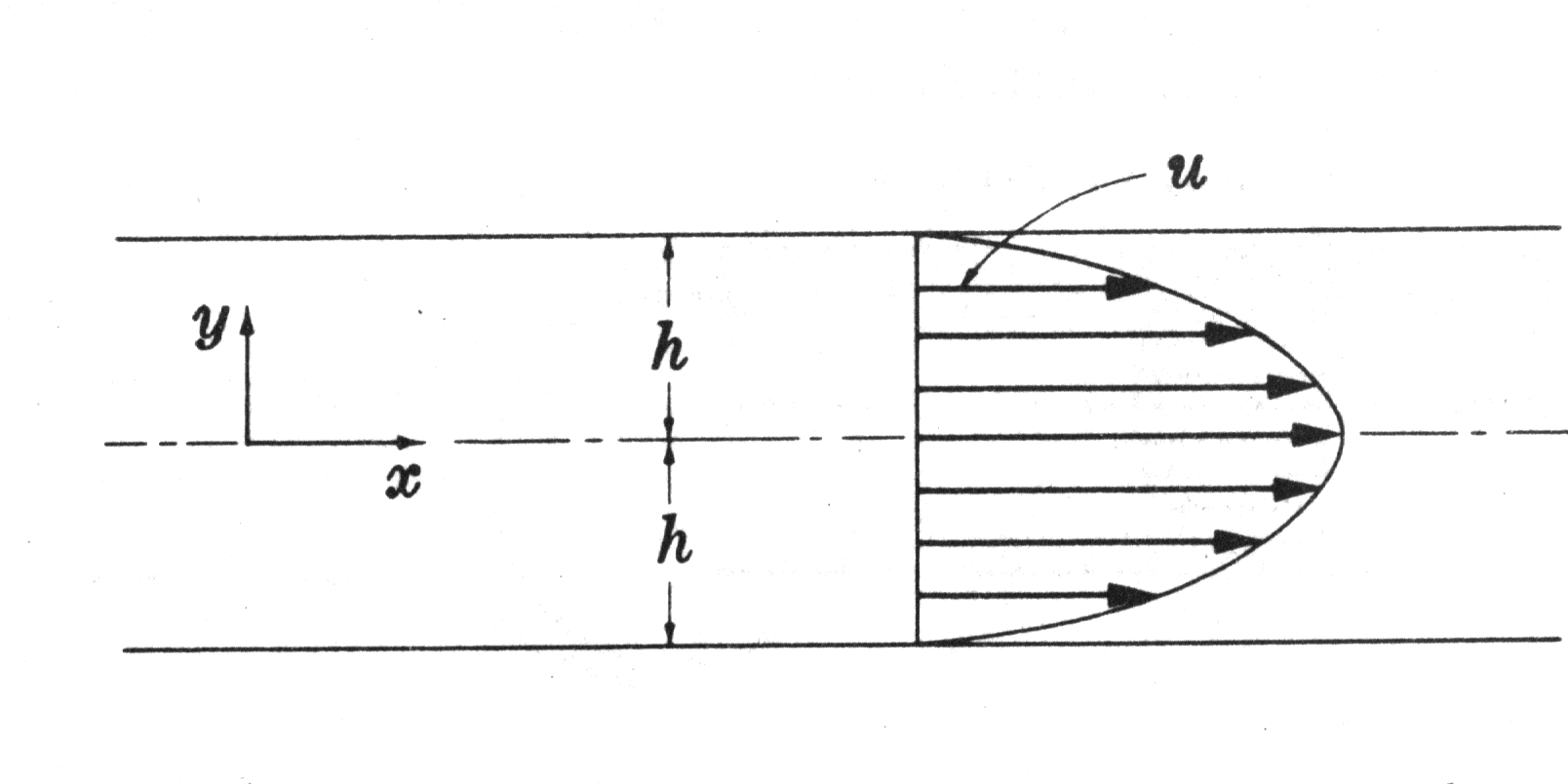
Nel primo caso il profilo di velocità è simmetrico rispetto all'asse centrale del tubo , nel secondo caso il profilo di velocità è simmetrico rispetto al piano equidistante della due superfici . L'andamento del profilo è parabolico in entrambi i casi , il vettore velocità assume il valore massimo nel vertice della parabola .
Pertanto , per la risoluzione dei problemi fluidodinamici , tipicamente si utilizzano delle simulazioni numeriche al calcolatore ; i problemi di calcolo fluidodinamico sono di gran lunga i problemi di calcolo numerico più difficili , tanto che per la loro risoluzione può essere necessario l'uso di un supercalcolatore. Tuttavia ,spesso a causa della eccessiva difficoltà nell'interpretazione degli esiti di queste simulazioni numeriche , i risultati possono non essere accettabili soprattutto per ragioni di sicurezza (per esempio nella simulazione del volo di un aereo) . Per questo motivo si preferisce un approccio molto più affidabile che trova il suo fondamento nella teoria dei modelli , l'utilizzo del calcolatore avviene a posteriori per cercare ulteriori conferme degli esperimenti realizzati su dei modellini in scala dei sistemi che studiano.
2
CENNI ALLA TEORIA DEI MODELLI
La teoria dei modelli ha una validità generale che trascende dai confini della Fisica tecnica , infatti essa è applicabile a molte altre discipline scientifiche . Secondo questa teoria è possibile studiare un sistema fisico attraverso un suo modello adimensionale. E' possibile in altri termini effettuare la adimensionalizzazione di un problema estraendo da esso dei parametri o raggruppamenti adimensionali che lo caratterizzano e che costituiscono le cosiddette condizioni di similitudine. Due problemi sono simili se hanno gli stessi parametri adimensionali , ovvero la condizione di similitudine si basa sulla invarianza dei parametri adimensionali . In fluidodinamica il parametro adimensionale di riferimento è il numero di Reynolds (Re) .Per esempio dato un sistema fisico reale (una turbina , un aereo , una macchina da corsa) per studiarne il comportamento fluidodinamico con grande precisione utilizzando la teoria dei modelli si costruiscono dei modellini in scala del sistema stesso, aventi gli stessi parametri adimensionali , e si utilizzano questi modellini in laboratorio per verificarne le prestazioni . Un tipico apparato utilizzato in questo campo è la galleria del vento, in essa vengono inseriti i modellini in scala di veicoli e aerei i quali sono sottoposti ad un flusso d'aria , le gallerie del vento sono dotate di numerosi strumenti di acquisizione dei dati fluidodinamici che interessano ai progettisti ; in figura è mostrato lo schema di funzionamento di una galleria del vento :
Dunque dato un qualunque problema fluidodinamico occorre : scrivere le equazioni del moto , adimensionalizzarle, ricavarne i parametri adimensionali caratteristici . In base a questi dati poi , è sufficiente ricondursi alle soluzioni di pochi problemi "caratteristici" che sono già note . La teoria dei modelli è molto potente anche perchè consente di stabilire delle analogie formali non solo fra problemi all'interno di una stessa disciplina ma anche fra problemi apparentemente molto diversi che possono essere risolti allo stesso modo se presentano gli stessi parametri adimensionali . Una tipica analogia è quella fra lo studio dei corpi vibranti (es :sospensioni di una automobile) e un circuito elettrico RLC. Esiste anche una analogia fra il moto dei fluidi e lo scambio termico (analogia di Reynolds) che si evidenzia annullando formalmente il termine dovuto ai gradienti di pressione nell'equazione di Navier .
mailto:jacopo.aleotti@polirone.mn.it