Autore: Antonio Affanni
Matricola: 110717
Lezione del : 22/12/1998
Ore:16.30-18.30
Superfici alettate
E’ frequente l’utilizzo di superfici alettate per scambiare calore, infatti tale metodo è poco costoso e molto efficace quando il fluido di servizio ha coefficiente liminare h abbastanza basso. Proprietà principale dell’aletta è quella di aumentare la superficie di scambio e quindi ridurre la resistenza termica dovuta alla convezione del fluido di servizio, che, in questo caso, è l’aria circostante. Si veda, per una singola aletta, l’aumento della superficie di scambio rispetto ad una lastra piana.
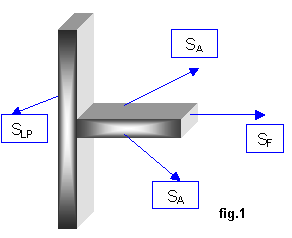
In fig.1 sono state poste:
SLP ,superficie della lastra piana;
SA, superficie dell’aletta;
SF, superficie frontale dell’aletta.

Allora sara`:
![]()
dove S è tutta la superficie alettata.Per il momento si trascuri la sezione frontale SF e si veda come varii la temperatura lungo l’aletta dalla lastra piana fino all’estremità libera, presumendo un andamento decrescente, come mostrato in fig.2.
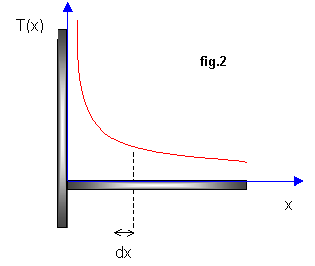
Per trovare analiticamente T(x) si dovrà considerare una striscia dell’aletta di larghezza infinitesima dx.
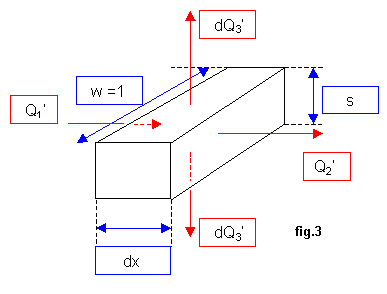
Si osservi la fig.3.
Per semplicità si è posta la profondità w =1. Inoltre i calori raffigurati in rosso sono in realtà calori scambiati in unità di tempo;tale significato ha l’apice posto a destra. Si è altresì scritto dQ3’ invece di Q3’ poiché lungo la striscia di larghezza dx si scambia una parte infinitesima di Q3’.Dalla fig.3 si vede che :
![]()
Inoltre si sa:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
Osservazioni :
a) Si è già posto w =1 quindi d’ora in poi verrà omesso.
b) l è la conducibilità termica del materiale dell’aletta.
c) La (1) è la legge di Fourier.
d) La (2) si ottiene facendo lo sviluppo di Taylor troncato al 1° ordine della legge di Fourier lungo il tratto dx.
e) La (3) è la relazione tra calore e temperatura per la convezione però anziché h è stato usato il coefficiente di adduzione a che comprende sia una trasmissione per convezione che per irraggiamento.
f) Tx e T¥ indicano rispett.: T(x) e limx® ¥ T(x).
Sottraendo membro a membro la (1) e la (2) si ha:
![]() (4)
(4)
Allora dalla fig.3 e dalle (3) e (4) si deduce che :
![]() (5)
(5)
Attraverso semplici passaggi algebrici si perviene alla relazione:
![]() (6)
(6)
Sapendo inoltre che ![]() ,allora la (4) sarà :
,allora la (4) sarà :
![]() (7)
(7)
Posti :
![]() la (7) prendera` l'aspetto dell’ equazione di Helmoltz :
la (7) prendera` l'aspetto dell’ equazione di Helmoltz :
![]()
![]() (8)
(8)
la cui soluzione q è data da
![]()
![]() (9)
(9)
Ora si tratta di vedere le condizioni al contorno.
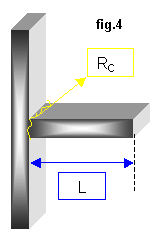
Condizioni al contorno per x = 0.
Innanzitutto è necessario stabilire come l’aletta venga fissata alla parete.Spesso infatti nel raffreddamento di componenti elettronici le superfici alettate sono avvitate sul componente, ciò implica che una piccola scabrosità dell’aletta (o del componente) può causare una ( seppur minima) resistenza di contatto che si indicherà con il simbolo RC .Tale resistenza alla trasmissione del calore è comunque minimizzabile tramite pasta di silicone o grasso.
Dunque il calore trasmesso dalla parete piana all’aletta sarà :
![]() (10)
(10)
Ove ![]() e il pedice "p" riferisce le grandezze alla parete .
e il pedice "p" riferisce le grandezze alla parete .
Inoltre dalla (9) si sa che q (0) = A + B. (11)
Si scrive, inoltre, grazie alla (9), che :
![]()
Dalle (10) e (11) si ottiene anche : -l m(B-A) = [q p - q (0)] /RC = [Tp - T¥ - A –B] /RC .
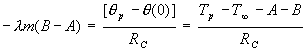 (12)
(12)
Condizioni al contorno per x = L
Approssimativamente , se L è abbastanza elevato, si sa che Q’(L) » 0.
Allora
![]() . (Poiché Q’ e' proporzionale alla variazione di temperatura lungo x)
. (Poiché Q’ e' proporzionale alla variazione di temperatura lungo x)
Sempre dalla (9) : ![]() (13)
(13)
Sostituendo la (13) nella (12) e facendo semplici passaggi algebrici si ottiene :
![]()
![]()
Infine dalla (9)
![]()
Ora si ponga QAL’º 2dQ3’ , ovvero il calore scambiato dall’aletta all’ambiente.
Dalla (3) si ottiene:
![]() (14)
(14)
l
a quale, integrata , dà :![]() (15)
(15)
Ora si vuole trovare il calore QP’ che viene scambiato dalla parete piana all’ambiente in una sezione equivalente a quella dell’attacco dell’aletta (quella sezione che in fig.1 era stata chiamata SF). Sicuramente sarà dovuto a convezione e irraggiamento :
![]() (16)
(16)
Avendo posto TF = T(L) » T¥ .
Si definisce guadagno dell’aletta G il rapporto QAL’/ QP’.
Dalle relazioni (15) e (16) si ottiene
![]() (17)
(17)
Si definisce ora efficienza dell’aletta e A il rapporto QAL’/ QAL,0’ ,avendo posto QAL,0’ la quantità di calore che l’aletta scambierebbe con l’ambiente se fosse tutta a temperatura costante.
Dunque :
![]()
Dalla (15)
![]() (18)
(18)
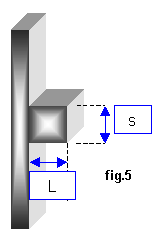
Esempio dell’ "Aletta tozza".
Si consideri ora un’aletta "tozza" , ovvero avente lunghezza L pari allo spessore s.
Questa condizione porterà a dimostrare che l’approssimazione fatta all’inizio riguardo alla trascurabilità della superficie frontale SF possa dare un errore elevato nei calcoli .
Grazie alle (17) e (18) si scrive il Guadagno in funzione dell’Efficienza.
![]()
Per come è stata definita, e A = 1, poiché QAL’ = QAL,0’, essendo L molto piccola.Inoltre per la condizione posta sopra, L = s .Ne consegue G = 2. Ciò è assurdo, in quanto l’aletta scambia calore da tre superfici, quindi si dedurrebbe G =3 . Con questo esempio si è mostrato il caso in cui si può commettere il maggiore errore nel calcolo del guadagno dell’aletta .Trascurando la sezione frontale si è ottenuto un errore del 50% !Per ovviare a questo inconveniente ,anche nei casi meno "estremi" (e quindi anche più realistici), è buona norma considerare una lunghezza
equivalente L’ posta : L’ = L + s/2 .
Superfici con più alette
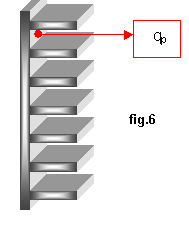
Si consideri ora il caso in cui invece di una sola aletta ci sia una superficie alettata .In fig.6 è stato posto qp il calore scambiato dalla parete per unità di superficie. Siano inoltre:
SAL la somma delle superfici esterne delle alette;
qAL la quantità di calore scambiata dalle alette per unità di superficie;
QTOT’ la quantità di calore scambiata da tutta la superficie;
STOT la superficie totale.
Ne consegue:
![]() (19)
(19)
Inoltre :
![]() (20)
(20)
Ciò deriva dalla definizione di Efficienza e dal fatto che:
![]()
Sostituendo la (20) nella (19) e risolvendo rispetto a e TOT si ottiene:
![]() (21)
(21)
![]() (22)
(22)
Si veda ora come varia l'efficienza dell'aletta in funzione dei fattori di forma nel grafico sottostante:
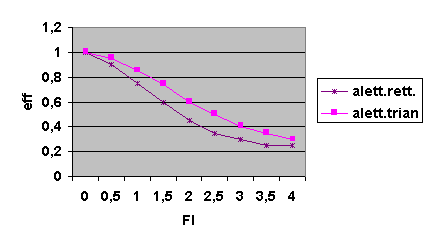
Le due curve indicano l'efficienza di un'aletta triangolare e rettangolare ed in ascissa è stato posto un numero puro che dipende dai fattori di forma; esso è il "coefficiente di snellezza" FL.
Tale snellezza e` definita come :
![]()
dove A indica il prodotto tra lo spessore s e la lunghezza L dell'aletta.
Esercizio
Si vuole conoscere la temperatura di una parete piana posta a raffreddare un processore. Essa è quadrata e di lato L = 50mm.Si vuole inoltre sapere se è necessaria una superficie alettata di raffreddamento. Siano dati:
Q' = 20 W , calore scambiato dal processore all'ambiente;
TA = 20°C , temperatura ambiente.
Soluzione
Si tratta di risolvere un problema di scambio termico tra la parete e l'ambiente.
Il calore si propaga nell'aria quindi vi sarà uno scambio dovuto a convezione e irraggiamento.
Si sa che : ![]() Dove h è il coefficiente liminare e S la superficie della lastra La convezione è naturale dunque entreranno in gioco i numeri di Grashof , Nusselt e Prandtl.
Dove h è il coefficiente liminare e S la superficie della lastra La convezione è naturale dunque entreranno in gioco i numeri di Grashof , Nusselt e Prandtl.
![]() ,(1e) ;
,(1e) ; ![]() ,(2e) ;
,(2e) ; ![]() , (3e);
, (3e);
![]() , (4e).
, (4e).
Avendo posto:
L: altezza dei piani verticali su cui si sviluppa la convezione (in questo caso coincide con il lato della lastra) (50mm.); g: accelerazione di gravità (9,81m/s2); b :coefficiente di dilatazione termica (che nel caso di gas è l'inverso della temperatura) (appr.1/333 °K-1); n : viscosità cinematica (16.10-6m2/s); m : viscosità dinamica (1,9.10-5 Pa.s ); cp: capacità termica a pressione costante (1009 J/°K.Kg) ; c,k: costanti sperimentali che variano al variare del tipo di convezione e del numero di Grashof. l : conducibilità termica (0,03 W/m.°K)
Tutte questi valori sono tabulati . Le incognite del problema dunque sono:
Si calcola il numero di Grashof imponendo una Tp di tentativo Tp =100°C.
![]()
Ora si calcola dalla (4e) il numero di Prandtl:
![]()
Si trova Gr.Pr » 1.093.222 .
Per tale valore le tabelle indicano, riferendosi alla (1e), c = 0,53; k = 0,25.
Ovvero :
![]()
Dalla (2e) si ricava il valore di h.
![]()
Approssimativamente dunque il coefficiente di adduzione varrà:
![]()
Dalla relazione che lega calore a temperatura per lo scambio convettivo,
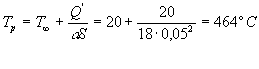
Tale temperatura è ovviamente troppo elevata per un componente elettronico, allora sarà necessaria una superficie alettata .Si stabiliscono le misure ponendo: La lunghezza delle alette (L) pari a 20mm.; Il loro spessore (s) pari a 3mm. ; La distanza fra un'aletta e l'altra pari a 3mm.
Ora calcolo il coefficiente di snellezza ,sapendo che la conduttività del materiale delle alette è
![]() , sarà:
, sarà:
![]()
Dal grafico possiamo ricavare un valore per l'efficienza pari a circa 0,93. Viste le dimensioni della lastra , lo spessore delle alette e la loro distanza, sarà possibile posizionare otto alette la cui lunghezza equivalente è L' = 21,5mm. Inoltre la superficie piana che scambia calore è attualmente la metà rispetto alla lastra senza alette e la superficie totale delle alette sarà sedici volte quella di una singola aletta.
![]()
Il calore totale scambiato sarà
![]()
Si vede che a tale temperatura il componente non rischia di danneggiarsi per surriscaldamento.